Improving Cloud Data Encryption Using Customized Genetic Algorithm

In the modern world where everyone has access to computers and can generate bulks of data at the click of a button and by the usage of applications on mobile phones, the risk of security breaches has also been increased. After the invention of cloud computing, most of the data that was previously kept offline is now being uploaded to the cloud

• [15] . With this technological advancement where we can access the data anywhere anytime, we also need to implement security measures to ensure that the data is safe from unauthorized access for misuse. These security measures include techniques that involve communication in such a way that it is kept secure from others/unauthorized users. To keep communication or data secure, many cryptographic schemes have been and are being developed over the years. The main objective of all these encryption schemes is to make it impossible or at least difficult for non-intended users/persons to get access to the secured data. Any encryption scheme involves two processes, the first process is encoding the original message/data into a coded message or cipher-text using an encryption key, and the second process involves decryption/decoding of the cipher-text into the original message/data using the decryption key [8].

There are two major types of cryptography: symmetric and asymmetric. Symmetric cryptography uses a method in which the same/single key is used for encryption and decryption processes [42], which means that the sender and receiver of the message or the creator and user of the data uses the same key for encrypting the data and then decrypting it. This type of cryptography has widely been used around the globe in many fields, i-e; ATM encryption, email privacy, and Secure Remote Access (SRA), etc. This type of cryptography is used in two modes, Block cipher, and Stream cipher. Block cipher algorithms use the data/message in the block form to encrypt and decrypt, they take the data and then divide it into different blocks of the same size to perform encryption processes on them. The Stream cipher system works on the streams of data. It combines the key with data in bit by bit or character by character mode. The encryption key used in this type of symmetric cryptography is relatively long and compared to the block type cipher systems.

As the algorithms based on symmetric cryptography use the same key for encryption and decryption, therefore there is always a need to use only secure key between the two parties. The key management is the only problem that lies in this system.

Asymmetric cryptosystems were introduced as an improvement in Symmetric cryptography. They use different keys for encryption and decryption processes. [43].The two keys used seem different but are alike in mathematical terms. The key used for data encryption is termed as the public key, and the key used in decrypting the data/message is termed as the private key [43]. Asymmetric Cryptosystems are widely used in secure communication and the schemes implementing digital signatures.

Both symmetric and asymmetric types are popular encryption techniques to secure the data and communication. Data Encryption Standard (DES) was the first standard to be adopted as a symmetric cryptography standard in 1977 [42] till the time it was superseded by Advanced Encryption Standard (AES) [38]. Despite been deprecated, DES is still widely used in several applications. DES and AES are the most popular standards among symmetric cryptography. In asymmetric cryptography, the most popular and most widely used technique is Rivest, Shamir, and Adleman (RSA) Algorithm [41].

All these mentioned techniques have been widely used to secure the data in the past decades but due to the advancements in technology and the advent of cloud storage, the data is now uploaded to the cloud for the ease of access. The problem lies in the need to decryption the data before use. If encrypted data resides on the cloud and that data is required for use, the conventional encryption technique would require the user to pass on the secret key to the cloud to decrypt that data, thus, that it can be used.

The passing of secret keys to the cloud and data is decrypted on the cloud; the data is susceptible to be misused by anyone who has/may have access to it. This problem makes these conventional techniques insufficient and inefficient when it comes to cloud storage [18].

This disadvantage can be overcome with the use of Fully Homomorphic Encryption (FHE) technique. FHE technique allows several calculations on the cipher-text without damaging or even changing the original text itself. For secure data processing in the cloud, FHE [18] can be used because this technique supports the execution of several operations on encrypted data. While FHE is implemented, if the data needed to be processed or used, it would take the arguments for the data and make the search on the encrypted data and generate results in the encrypted form based on those arguments. Those encrypted results can then be downloaded and decrypted for use. For data encryption/decryption, the FHE technique uses public/private keys just like other encryption techniques. The complexity of this encryption key determines the effectiveness/complexity of cipher-text. To make the encryption key more random and thus more secure, the genetic algorithm is used [22, 27].

Genetic Algorithm (GA) is a search-based algorithm, it is mainly used to solve optimization problems. The genetic algorithm is inspired by Darwin’s Theory of Evolution, therefore; they are based on the concepts of population, mutation, crossover, etc. The use of genetic algorithms in encryption techniques [19] has greatly increased in the last few years because they are secure in their implementation. Genetic algorithms are unique [29] and best suited in this problem [28] because using the properties of mutation and crossover, it can generate highly random and complex keys to use in encryption technique [24].

The work of genetic algorithm in cryptography was started in 2005 [36] and it has been worked upon to be used with different kinds of data to be encrypted, GA has also been used along with other encryption techniques [11]. The work to improve encryption by using GA has been done many times in different encryption techniques but, the work to improve the working of GA has quite not been done so far. The main focus of this research is to find the optimum values or customization of this algorithm so that the working can be improved. First, the optimum values of GA operators are set by experimenting with different combinations, and then local Intelligence is introduced in the algorithm for further improvement. The improvement is based on time and randomness to generate the Encryption key.

This research contributes towards the optimization of GA operators to find the optimum values for the generation of random Key in as little time as possible. We also used the Local Intelligence-based Algorithm to improve the results obtained with GA implementation. This study also provides a comprehensive comparison of Conventional GA and Local Information based implementation for the generation of a random secret key.

Section 2 reviews the literature and the background of all the related encryption schemes including Genetic Algorithm Inspired Cryptography (GIC), Improved Cryptography Inspired by Genetic Algorithms (ICIGA), Fully Homomorphic Encryption (FHE). Section 3 deals with the details and the implementation of the proposed methodology to improve conventional GA. Section 4 includes the results generated by the implementation of the proposed algorithm and its comparison with the conventional technique. Section 5 contains the summary and future work related to this technique.

2.    Background

Cryptography is mainly divided into two types, Symmetric Cryptography [42] in which the key used for encryption is also used for decryption of data. The second type is Asymmetric Cryptography [41], in which two different keys are used for encryption and decryption called public and private keys. Work on symmetrical cryptography has remained relatively stationary. However, during the last decade, many approaches symmetric cryptography have been proposed that include genetic algorithms.

• 2.1.    Genetic Algorithm

• 2.2.    Genetic Algorithm Methodology

Genetic Algorithm or simply (GA) is a search-based algorithm, it is mainly used to solve optimization problems. The genetic algorithms is inspired by nature therefore; they are based on the concepts of population, mutation, and crossover. The use of genetic algorithms in encryption techniques is greatly increased in the last few years due to their random nature. Genetic algorithms are unique and best suited in our problem because using the properties of mutation and crossover, highly random and complex keys can be generated to use in the encryption technique [27].

This section presents all the steps and methods of using the Genetic Algorithm. The following are the standard operators of the genetic algorithm.

• A.    Initial Population

It can be called the initial input values for the Genetic Algorithm. Different input values are selected for crossover and offspring or new solutions are produced from them.

• B.    Fitness Function

In each iteration, parents are evaluated under specific criteria if they are near to optimum solution or reached the solution criteria. This evaluation is called a fitness function.

• C.    Crossover

In Crossover, small portions of two parents/values are replaced with one another to generate new child/values.

• D.    Mutation

In Mutation, some uniqueness is introduced by changing bits at random in new values to make them more random.

• E.    Selection

In the last step, the best value is ‘selected’ as a solution.

The following figure 1 shows the 1 generation cycle of the genetic algorithm [39].

The initial population contains all the sample input or initial values to start the algorithm. In the standard genetic algorithm methodology, these initial values are consisting of all the proposed solutions to the problem.

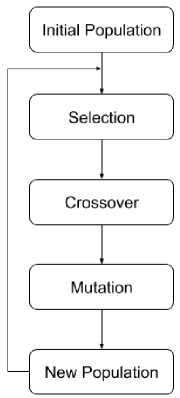
Fig.1. Genetic Algorithm Operators as One Complete Cycle

In the next step, these proposed solutions or initial values are then sorted, filtered, and selected for further optimization. Different techniques are used for selection from the initial population that depends on the situation and conditions of the problem, this situation or condition of the problem is also defined as the fitness function. This fitness function along with the selection method is used to select the values for the next procedure. Different selection methods that are used for different problems are as follow [17].

• 1)    Roulette Wheel Selection

• 2)    Rank Selection

• 3)    Steady-State Selection

• 4)    Tournament Selection

• 5)    Elitism Selection

• 6)    Random Selection

The fitness function along with any of the above selection methods is used to sort, filter, and select the values for the next procedure called crossover. Each of the above-mentioned selection methods has its implementation and benefits, therefore the selection method can have a great effect on the results generated at the end of each cycle. The purpose of each selection method can be different based on the problem statement therefore it is crucial to choose the best-suited selection method for the problem.

Different crossover techniques are used to mix or interchange different bits/ values of the parents to develop offsprings. Different crossover techniques that are used are as follow [12];

• 1)    Single-point crossover

• 2)    Two-point and k-point crossover

• 3)    Uniform crossover

• 4)    Crossover for ordered lists

Just like the selection methods, all the crossover techniques have different uses and purposes. Using a specific crossover technique suited to the problem might have a higher effect as compared to other crossover techniques.

After the off-springs are generated, these are passed through one more procedure of mutation to generate some new values/characteristics to be somewhat different from their parents.

Different mutation techniques used are as follow [12];

• 1)    Bit-String Mutation

• 2)    Flip Bit Mutation

• 3)    Boundary Mutation

• 4)    Non-Uniform Mutation

• 5)    Uniform Mutation

• 6)    Gaussian Mutation

• 7)    Shrink Mutation

• 2.3.    Genetic Algorithm (GA) in Cryptography

  A symmetric system was developed in 2006, which is a block-based encryption scheme named Improved Cryptographic Inspired by Genetic Algorithm (ICIGA) [35]. In this technique, text document/data is first converted into binary form and then divided into blocks of the same size. The encryption key is generated as the encryption progresses therefore the size of a block and key size must be set to the same size and they can be set as per the user’s interest. This ICIGA technique is an improvement of the already proposed technique Genetic Algorithm Inspired Cryptography (GIC) by the same authors [36].

After the mutation technique is applied, the child is ready for the next cycle as a parent. The fitness value is calculated of the new generation and then selection technique is applied for selecting the parents for the next generation until an optimized solution is found.

In 2012, [31] proposed an approach that used GA with a pseudorandom sequence. This technique could easily be used in industrial level applications that have a use for e-security image applications for encryption and decryption. Several images were encrypted and decrypted with this approach and the experimental results showed real-time data protection with a high throughput rate. Many other genetic algorithm techniques have also been used for image encryption [23, 30, 32] where different operators of the genetic algorithm were applied on image pixels and a key was generated as a result to decrypt the image back to its original form. Genetic algorithm has also been used along with other techniques to improve image encryption results [11].

The genetic algorithm is also used in network security [1, 13, 21] where the data to be sent through a network is converted into binary form and then different GA operators are applied to randomize these bits so that the original data can be encrypted. The encryption key is also transmitted at the end of the data stream to the receiver to decrypt the binary encrypted data.

In recent years, many authors have used GA in their encryption techniques to secure plaintext [9, 21]. In this technique, the authors have customized the GA and used two different keys entered by the end-user/sender of the message. Then those keys are merged, and different GA operators are applied to get the cipher-text. Others have used GA to generate a random key using GA and then using that random key to encrypt the data [4]. In the same year, another study was performed to use GA operators to generate a randomized key and finding it a better technique as compared to other key generation techniques [7]. On the other hand, a technique that uses GA along with Random Number System (RNS) for encryption and decryption of data was implemented the same year [5]. Another technique that customizes GA along with some arithmetic and logical operators to secure the data has proved to be very effective [14].

Other than image encryption and text encryption. There are many other fields where GA has been implemented for encryption purposes such as cellular automata, non-linear optimization [26], Quadtree Approach [37], and even in Correlation Power Analysis (CPA) to find the correct key [10]. It has also been implemented in Decision Tree [3] and Wireless Networks to preserve the energy of the nodes [2].

GA has also been used in asymmetric cryptographic techniques that use two different keys namely public and private keys for encryption and decryption [25, 27].

Other than Cryptography, it has also been used in the improvement of path maintaining of mobile robots [6].

• 2.4.    Fully Homomorphic Encryption (FHE)

A solution to this problem was first introduced by [40], these authors first gave the idea of Privacy Homomorphic Encryption. Nowadays this concept is used as Fully Homomorphic Encryption or FHE instead of Privacy Homomorphic Encryption.

This scheme of FHE is considered as an algorithm for cryptography that supports arbitrary computations on cipher-text without needing to decrypt or reveal it. It was an open problem until [33], Gentry improvised and implemented the idea of Private Homomorphism into Fully Homomorphic Encryption. This technique is mostly used by different third-party security providers because it can be used for secure searches on huge data i.e.; private information retrieval without decryption.

Craig Gentry was the first person who invented an encryption scheme that was fully homomorphic based on ideal lattices [34]. Gentry’s innovation can be summarized into three stages including

• 1)    the construction of some-what homomorphic encryption

• 2)    “squashing” the decryption until it is sufficiently straightforward to be controlled within the capacity of somewhat homomorphic encryption

• 3)    “Bootstrapping” technique to get the FHE scheme.

3. Research Methodology

• 3.1.    Using a Genetic Algorithm

Since Gentry distributed the initial FHE system, this innovative discovery became a dynamic research subject and there has been a huge interest in this scope. Researchers have tried to change and improve the conventional technique by using e.g., integers instead of lattices, or learning with an error. Consequently, the execution of the following schemes has been improved. But as a conclusion, FHE still needs improvement in the number of operations performed on the encrypted text and its limitations on efficiency, etc [20].

This technique uses a random process for the selection of equal-sized blocks of the sample of input text converted into binary, this process is called block encryption. This process of the selection/conversion to equal-sized blocks is dependent on the selection of secret key length size, therefore the size of the blocks is set according to the size of this secret key. The choice of key length size is given to the user who is encrypting the data before starting the encryption procedure. The encryption key generation and block encryption are dependent on this choice. If the user doesn’t select the key length size then a default key length size is selected, the default key size depends on the parameters.

After the key length is defined, the plaintext is converted into binary code and divided into two equal parts namely the right side and left side. After that, the Encryption Key is generated using the local information-based technique in figure 2. The first or the right part is broken further. It is then used along with encryption key and processed under GA operators; the final step consists of ciphering this binary form of the text. After all the blocks are encrypted, they are combined back together to form the ciphertext.

This process can be explained in the following points.

• 1)    Sample Data

• 2)    Encryption Key size.

• 3)    Setting the Block size according to the Encryption Key size.

• 4)    Convert Plaintext into Binary.

• •    Each letter of the plaintext is converted into ASCII values.

• •    ASCII values are then converted to the respective Binary values using the Division-remainder technique.

• 5)    Divide Binary code into two equal parts.

• 6)    Generate Encryption key.

• 7)    Merge Right part that was generated in step 5 with the generated Encryption key in step 6.

• 8)    Process the merged result in the previous step under Genetic Algorithm operators.

• 9)    Merge the result with the left part that was generated in step 5.

• 10)    The result is ciphertext.

Above mentioned steps can be simplified into the flow diagram given in figure 2;

Step 6 mentioned in the above methodology that involves the generation of encryption Key has more than one implementation. The key generated in that step has the most important role in the whole encryption procedure because it is used to encrypt or decrypt the data. Therefore, the study is focused on this step and thus it has different implementations.

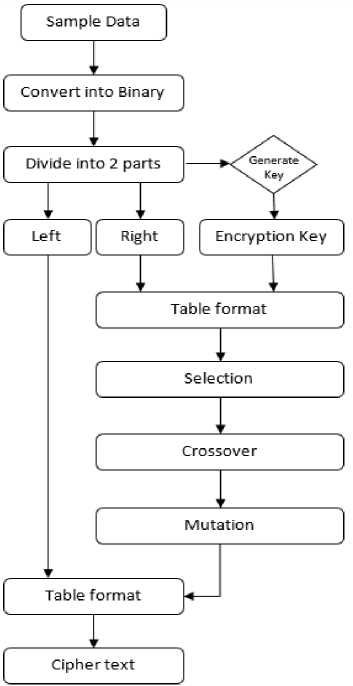
Fig.2. Encryption Methodology using Genetic Algorithm

The first implementation is based on standard GA operators and the results are kept for the comparison purpose. Different operators (number of generations, population size, mutation rate, crossover) of the above implemented standard GA in step 6 for the generation of the encryption key, are changed (optimized) to study the impact on its randomness and complexity of the generated encryption key.

By changing the operators means that the values of each operator are changed, and the results obtained are stored to review the changes in the randomness of the final key generated and time spent to generate that final key. For example; the total population is changed in each test to observe the time taken to generate the final key and its randomness and how many generations does it take to generate a highly random key in minimum possible time. Last but not least, changes in the mutation rate and different crossover techniques are implemented to observe the changes in the results obtained.

After this implementation and result collection, the second implementation is performed, which is based on the proposed technique. The proposed technique is based on the local Intelligence. In this implementation, the operator of the crossover and mutation that were used in standard GA implementation is replaced with local Information based operators.

• 3.2.    Local Information based Key Generation

After the implementation of the above-mentioned customization and result obtained, some steps of this GA are replaced and introduced with some additional steps of local intelligence. Local intelligence consists of two operators (best/worst value of chromosome at the gene level and a random bit generated at each iteration). This local intelligence is then processed with the previous iteration values of each binary key obtained under a specific mathematical pattern, as the goal here is to achieve total randomness while keeping the time factor. This local intelligence is used to get more random behaviour as a proposed GA oriented technique.

Below are the operators of the proposed GA oriented technique;

• 1)    Initial Population

• 2)    Random Selection

• 3)    Local Intelligence

• •    Best/worst or random value (depending upon the fitness function)

• •    Random bit

• 4)    New Population

Above mentioned steps can be simplified as presented in figure 3;

• Fig.3.    Local Intelligence-based operators

The implementation of the above technique allows us to test and compare the results obtained with standard GA as well as its customized operators. This allows us to better understand the reasons to implement such a technique and its effectiveness.

Algorithm for local intelligence-based methodology can be seen below;

• 1)    Initiate all the K population with binary random strings.

• 2)    Initiate the velocity of each parent for the initiated population.

• 3)    Compute fitness of every parent by the given fitness function.

• 4)    Repeat until the result found or reached the number of iterations.

• •    Select a parent at random.

• •    Generate a random bit.

• •    Multiply the random bit with each gene of the selected parent.

• •    Update velocity of each gene as below;

V im (n) = V im (n) + (Φ + X im )

In the above equation (1), V_im ( n ) is the velocity of the m‘^h gene of the i t parent in the n^th iteration. X_im is the m‘^h gene of the i t parent and Ф is the random number in floating points.

• •    Convert each gene value into binary.

• •    Update population.

• 5)    Stop

A flow diagram of the above-mentioned methodology can be seen in figure 4;

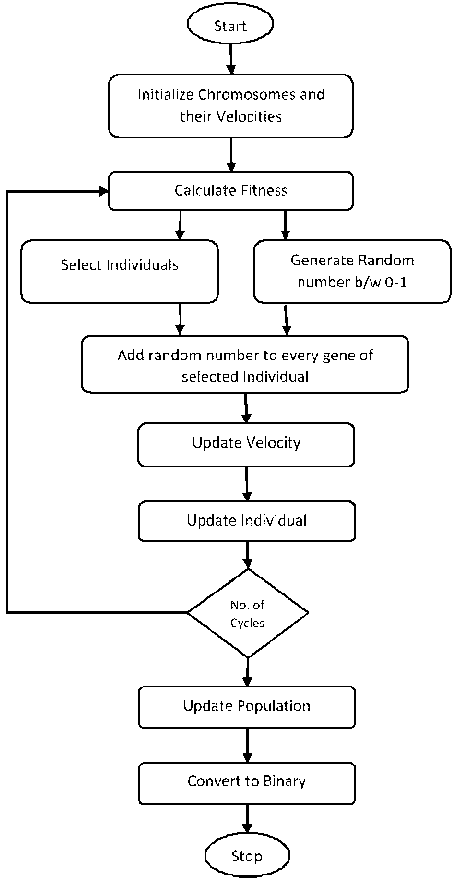
• Fig.4.    Local Intelligence-based Algorithm

4.    Result and Discussion 4.1.    Implementation of Conventional Approach

The local intelligence part promises to be faster as compared to the standard GA technique and reliable as much. The best / worst value step and random bit step fully overtake the crossover and mutation steps of standard GA therefore it promises as much randomness as well.

The new population generated after implementing local intelligence operators are evaluated under fitness function and it works just like GA to produce new generations with the benefit of being faster.

After the above implementation, the results are analyzed and compared for time and complexity.

The following values/parameters are proposed for the testing of this algorithm.

• •    Key size: 64

• •    Number of generations: 500, 1,000, 2,000, 5,000, 10,000.

• •    Population Size: 32, 48, 64, 128

• •    Selection type: roulette-wheel, random

• •    Crossover type: random, one point, two-point

• •    Mutation rate: 0.001, 0.03

The execution of this algorithm is done in java. Time varies from iteration to iteration, which depends on the load on processor and RAM used in each test, therefore, an average of values is taken for comparison.

Initially, when the lowest values are used with only 500 generations, 32 population size with 0.001 mutation rate, it quickly generates the final key in just a blink of an eye, but the randomness of the key is also compromised because of a very low number of generations. As the values of the GA operators are increased, time is taken to generate the final key also increases but it ensures high randomness in the final key. As this study is focused to find the threshold point of values to generate a highly random key in the lowest possible time, therefore, using a mixture of all the sample values of GA operators is necessary to cover all the points from minimum to maximum.

In the following study, it is observed that the time taken to generate the key with the lowest sample values of GA operators is 0.045 milliseconds and the time taken to generate the key with highest values of 64 Population and 10,000 Number of Generations only took 0.74 milliseconds which is still impressive. All the observed values in this test can be seen in the following tables.

Table 1. Standard Ga Implementation with Population ‘32’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 32	0.084	0.147	0.27	0.634	1.235

Results of Table 1 are generated with the initial population (P) of ‘32’, the time is taken gradually increases with the number of generations (G). As this is the first observation, therefore the results cannot be compared to or analyzed as good or average.

Table 2. Standard GA Implementation with Population ‘48’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 48	0.117	0.207	0.389	0.934	1.835

In Table 2, the results generated are based on the initial population (P) of ‘48’, as it can be observed that it takes about 40% more time to complete the same number of generations when running with ‘48’ initial population as compared to the Table 1 with ‘32’ initial population.

Table 3. Standard GA Implementation with Population ‘64’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 64	0.147	0.269	0.513	1.239	2.427

The values in Table 3 are a result of implementing the initial population (P) of ‘64’, as it can be observed that the time increase is significant for the initial value of generations (G) ‘500’. But it is certainly less significant of about 25% as compared to 40% in Table 2.

Table 4. Standard GA Implementation with Population ‘128’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 128	0.277	0.524	0.998	2.479	4.891

As we proceed further with the initial population (P) of ‘128’ in Table 4, the population size is doubled as compared to population ‘64’ in Table 3, but we also observe that the time taken has been significantly increased from about 75% if Table 1 with population size ‘32’ and Table 3 with population size ‘64’ are compared, which is also double the population size. The time is increasing from 75% to about 90%.

• 4.2.    Implementation of Local Information Approach

When the above implementation is complete and the results are gathered, the parameters are changed and the local intelligence factors are applied instead of crossover and mutation operators of the standard GA to observe the changes in the time taken for the algorithm to run and the randomness of the generated encryption keys. The following are the values/ parameters of the customized algorithm based on local intelligence.

• •    Key size: 64

• •    Number of generations: 500, 1,000, 2,000, 5,000, 10,000.

• •    Population Size: 32, 48, 64, 128

• •    Selection type: roulette-wheel, random

• •    Local Intelligence Chromosome value: Best value

• •    Local Intelligence Bit type: Random Bit

Other computer machine parameters are the same as were with conventional GA implementation, the coding and execution of the above mentioned can also be observed in Appendix 1. The difference in the generated results can be seen in the following Figure 5;

Fig.5. Local Information with Population ‘32’

Above values can be observed in Table 5

Table 5. Local Information Implementation with Population ‘32’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 32	0.045	0.0573	0.0733	0.092	0.15

The values in Table 5 are the result of the initial population (P) of ‘32’ with a gradual increase in the number of generations from ‘500’ to ’10,000’. As it can be seen that the initial value of time is just ‘0.045ms’ which is almost half the time taken to complete ‘500’ generations as compared to the conventional approach (Table 1) with the same parameters, thus the initial observation shows that the customized approach is more than twice as fast with ‘500’ cycles in Table 5 as compared to Table 1.

Now let’s calculate the executed time with the population size ‘48’.The results can be organized in the form of the following table.

Table 6. Local Information Implementation with Population ‘48’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 48	0.057	0.072	0.104	0.181	0.42

In Table 6, the increase in time taken to complete ‘500’ generations with ‘48’ population is ‘0.057’, which is an increase of around 26% time as compared to Table 5. It is a considerable improvement of 14% less time as compared to the difference between Table 2 and Table 1. It can also be observed that Table 6 approach with ‘500’ cycles is more than 100% faster as compared to the approach in Table 2.

Let’s move forward with the population ‘64’ and observe the executed time.

Table 7. Local Information Implementation with Population ‘64’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 64	0.072	0.097	0.153	0.322	0.74

In Table 7, using the initial population of ‘64’ takes ‘0.072’ seconds to complete ‘500’ iterations, which is also about 26% as compared to Table 6. It is also to be observed that the increase in time is very uniform as compared to the difference between Table 2 and Table 3 which provided 40% and 25% time difference respectively which is very irregular. The approach in Table 7 with ‘500’ cycles also proves to be about 100% faster as compared to Table 3 with the same parameters.

Now let’s try the population size ‘128’ and see what difference does it make in regards to time executed.

Table 8. Local Information Implementation with Population ‘128’

	Number of Generations
	G=500	G=1000	G=2000	G=5000	G=10000
Population (P) = 128	0.137	0.262	0.592	1.012	1.5

In Table 8, the initial Population (P) is ‘128’ with ‘500’ generations, and time increase can be observed to be about 90%. The time increase is understandable because of the 100% increase in the initial population from ‘64’ to ‘128’. But it is to be observed that the approach in Table 8 is twice as fast as compared to the approach in Table 4 with the same parameters.

• 4.3.    Discussion

  When the standard algorithm was implemented by [15] it took 3.5760 milliseconds to generate the randomized key with the same values. The only major difference in these two studies is that of the customization of GA and its operators. The customization of GA operators alone can show to be effective but when coined with local intelligence it is observed that the best results can be obtained.

The time complexity and randomness by using customized GA is really impressive as compared to the standard GA implementation. Even if used on a low-end computer, it is effective because the time difference is marginal in the case of customized GA oriented technique. The implementation summary of the customized GA and its comparison with (Alkharji & Liu, 2017) is provided in Table 9;

		Number of Generations
		G=500	G=1000	G=2000	G=5000	G=10000
Population Size	K=32	0.1560	0.2030	0.3440	0.7500	1.4389
	K=48	0.187	0.2960	0.5160	1.1720	2.3130
	K=64	0.2500	0.4370	0.7650	1.8280	3.5760

It can be observed in Table 9 that the population size ‘32’ takes ‘0.1560’ seconds to complete ‘500’ cycles which is the lowest time with minimum parameters, and it takes ‘3.5760’ seconds to complete ’10,000’ cycles with ‘64’ initial population size which is the highest time with maximum parameters provided. When it is calculated, we can find that the time difference from minimum parameter values to maximum parameter values is ‘3.42’ seconds, which converts to about ‘22’ times the initial time.

Table 10. Running time of Operator Customized Conventional GA

		Number of Generations
		G=500	G=1000	G=2000	G=5000	G=10000
Population Size	K=32	0.084	0.147	0.27	0.634	1.235
	K=48	0.117	0.207	0.389	0.934	1.835
	K=64	0.147	0.269	0.513	1.239	2.427

It can be observed in Table 10 that the population size ‘32’ takes ‘0.084’ seconds to complete ‘500’ cycles which is the lowest time with minimum parameters, and it takes ‘2.427’ seconds to complete ’10,000’ cycles with ‘64’ initial population size which is the highest time with maximum parameters provided.

Table 11. Running time of Local Information based Approach

		Number of Generations
		G=500	G=1000	G=2000	G=5000	G=10000
Population Size	K=32	0.045	0.0573	0.0733	0.092	0.15
	K=48	0.057	0.072	0.104	0.181	0.42
	K=64	0.072	0.097	0.153	0.322	0.74

In Table 11, It can be observed that the population size ‘32’ takes ‘0.045’ seconds to complete ‘500’ cycles which is the lowest time with minimum parameters, and it takes ‘0.74’ seconds to complete ’10,000’ cycles with ‘64’ initial population size which is the highest time with maximum parameters provided. When these values are compared with Table 9 and Table 10, we can easily observe that these values supersede greatly the time difference and time taken to complete any given number of cycles with any given population size.

• 4.4.    Time Complexity

• 4.5.    Degree of Randomness

The time is taken to generate the final encryption key as can be observed below, increases as the number of generations and the population size increases, but it is still under a second. When the minimum values are used, the difference in time is negligible for different population sizes. As the number of generations increases, the time difference in different studied population sizes can be observed to increase rapidly.

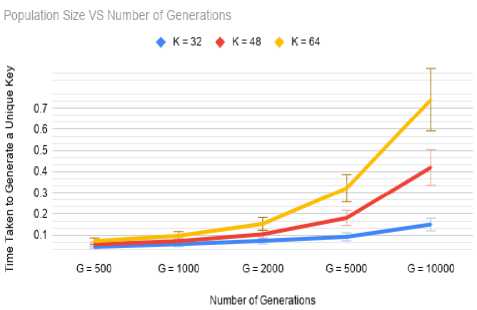
Fig 6. Time Complexity of Local Information based Approach

Figure 6 shows that even after 10,000 generations and initial population size of 64, it still can generate the nonrepeating and highly random key in under a second and these are not even the threshold values because these are the highest values used in the study.

Therefore, even the highest values used in the study involving local intelligence-based implementation are sufficient enough to generate completely random and time-efficient keys as compared to the other implementations in the study.

The degree of randomness is calculated to find the uniqueness and correlation of the final generated keys with previously generated final keys. In each test, it takes 10,000 iterations to complete and generate a final key and the value is converted into decimal and stored. Later on, all the stored values are compared and observed the correlation with all the other generated keys and to find any sequence to the generated key.

Table 12. Degree of Randomness for Customized Algorithm

742	972	912	976	806	779	469	997	488	467
671	326	903	186	809	901	114	179	94	215
992	801	859	855	195	841	451	785	684	207
542	332	191	597	247	301	931	539	551	753
225	90	228	190	668	624	786	425	754	725
694	401	481	212	394	810	678	364	459	279
795	357	781	115	996	890	126	275	563	293
174	626	143	333	675	534	595	1014	540	103

Test results in Table 12 have been performed on a key length of 10 x 10 to keep it simple to observe the results but the actual key length size is 64 x 64 and it will be even less susceptible to be cracked because it has been found in the sample key length of 10 x 10, that the final keys generated are random and unique. The correlation of the final key is '0' with every previously generated key. This means that every final key recorded is uniquely different than any other keys already generated and there is no sequence to these generated keys and can be seen in Table 12.

5.    Conclusion and Future Recommendations

The implementation of the conventional technique of GA is very effective with respect to time, complexity, and randomness that compared to other encryption techniques [15] as mentioned in table 9. When the operators of this conventional technique are customized, it can produce impressive improvements concerning time, which can be observed from table 1 to table 4. The difference in both operator's customized GA implementation and the conventional GA implementation can be observed that we compared to table 9 with table 10.

It can be observed in table 9 that it can take up to '0.1560 ms' to complete '500' generations with '32' initial population but table 10 showed that with the same parameter values, it takes only '0.084 ms' to complete. The improvement in time is more than 80% for the initial parameter values implemented with operator customized GA. For the highest parameter values, it can be observed that in table 9 the conventional GA takes '3.576 ms' to complete '10,000' generations with '64' initial population. Now , table 10 shows that with the same parameters of the initial population of '64' and '10,000' generations, it only takes '2.427 ms' which is more than 30% time improvement as compared to the conventional implementation. The above comparison is only for the conventional GA and its improvement by customizing its operators. Now let's observe the results with local intelligence-based Implementation. In table 11 the implementation shows that the minimum parameters of the initial population of '32' with generation '500' result take '0.045 ms', which is almost half the time taken as compared to the operator customized GA or improved GA implementation in table 10. The highest values of the initial population of '64' with generation '10,000' takes '0.74 ms' which is more than 200% time improvement as compared to the improved GA implementation table 10. That means the local information-based approach proves to be 2 times faster as compared to the conventional GA approach.

After observing the above comparisons, we can conclude that every result with local intelligence-based implementation is improved and better concerning time as compared to all the previous implementations.

Using the genetic algorithm for generating a random encryption key has been very effective for the past decade but the full potential in this regard has not been reached. This study provides insights on how to customize this algorithm for gaining maximum potential and best results in the sense of randomness concerning time. It has proven to be very effective to customize this algorithm to get the best results out of this algorithm.

This algorithm has a lot of potential for use in the encryption systems. Many have done some exceptional work in implementing a genetic algorithm in different encryption schemes in the last decade and it shows very good results as it is. But, as the volume of data has also been increased and is increasing because of the advent of cloud storage, therefore; there the work must be done to increase its efficiency in any or all regards of time, complexity or randomness, etc. The one implementation that was focused in this research is to improve its performance with respect to time without affecting the randomness. Some more studies are also needed to increase the randomness even more or increase the complexity of this algorithm. So, much work can be done to further improve this algorithm and use it with any encryption schemes.

Appendix A public static final int size = 32;

public static final int keySize = 64;

public static final int loopSize = 500;

public static boolean check = true;

public static Individual[] indv;

public static tempIndividual[] previousIndv;

public static tempIndividual[] tempIndv;

public static Population myPop;

public static Individual indvidual;

public static int[] randInt = new int[5];

private byte[] genes = new byte[size];

public static void main(String[] args) {

//====================

//Calculate start time of the loop long startTime = System.nanoTime();

myPop = new Population(size);

indv = new Individual[size];

previousIndv = new tempIndividual[size];

tempIndv = new tempIndividual[size];

for(int j = 0; j < size; j++)

{

Individual in = new Individual();

in.generateIndividual(); indv[j] = in;

} for(int k = 0;k < 2; k++)

{ randInt[k] = 222;

} saveTempIndv();

for (int i = 0; i < loopSize; i++)

{ if(check)

{ updateVelocity3();

previousIndv = myPop.tempIndv;

} else

{ updateVelocity3();

previousIndv = myPop.tempIndv;

} updateParticle();

} convert2binaryv2();

//Calculate end time of the loop long endTime = System.nanoTime();

long totalTime = endTime-startTime;

double tSeconds = ((double) totalTime)/ 1E9;

//Display Algorithm End Summary

Appendix B public static void updateVelocity3()

{ for(int i = 0; i < 2; i++)

{

Random rand = new Random();

int randValue = rand.nextInt(size);

if( i == 1)

{ while(randValue == randInt[0])

{ randValue = rand.nextInt(size);

}

} randInt[i] = randValue;

for(int j = 0; j < keySize; j++)

float cross = fi;

float getvelocity = myPop.velocities[randValue].getvel(j) + cross;

myPop.velocities[randValue].setvel(j, getvelocity);

}

} check = false;

}

Appendix C public static void updateParticle()

{ float result = 0;

for (int i = 0; i < 2; i++)

{ int randValue = randInt[i];

for (int j = 0; j < keySize; j++)

{ result = myPop

.velocities[randValue] .getvel(j) + previousIndv[randValue] .getGene(j);

myPop

.tempIndv[randValue] .setGene(j, result);

}

}

}