Improving the Prediction Rate of Diabetes using Fuzzy Expert System

Published Online September 2015 in MECS DOI: 10.5815/ijitcs.2015.10.10

Diabetes is a very common disease nowadays among the people of all age groups and has become a major health problem. With the rise in cases of diabetic patients there is a need of a reliable and accurate system that can diagnose the diabetes with a great accuracy at its early stage. The medical diagnosis of disease involves the patterns of observable symptoms and the result of diagnosis reports of test. But various costs and risks are associated with these tests. Various techniques and different systems have been proposed by the researchers to diagnose the diabetes, but the accuracy and efficiency of the prediction of diabetes is not so significant. All the developed expert systems aimed to diagnose the diabetes based on some parameters but there are some other parameters that had not been discussed so far.

The existing systems have various drawbacks like some were used for a particular type of dataset, some needed dataset of good quality. Therefore there is a need of a system of good quality that considers all the parameters, uses the best technique and predicts the diabetes with greater accuracy. Fuzzy logic and expert system are important and very promising techniques in medical environment as it incorporates the knowledge and experience of physician and based on that information the system will predict the diabetes. With the help of fuzzy rule-based system we can avoid cost of conducting the test for the diabetes diagnosis. The proposed system solves the problem by selecting a subset of useful feature from a set of features. It also proves to improve the diagnosis accuracy using fuzzy rule-based classification system and by selecting important and useful features.

This paper consists of seven sections. First section explains the introduction of this paper. In the second section the detailed problem of diabetes is discussed with its types. Third section deals with the fuzzy concept which includes fuzzy sets, their operations and fuzzy inference system. Fourth section discusses the related work in the field of fuzzy logic in medicine, diabetes diagnosis and blood pressure regulation. Fifth section is related to the proposed work in which we have discussed the architecture of proposed system, used dataset, fuzzy verdict mechanism and proposed algorithm. Sixth section shows the experimental results and the fuzzy rules used in the system. Finally seventh section describes the conclusion on which we have arrived and the last section of this paper shows the references which we have taken for this paper.

• II.    Diabetes

Diabetes is also known as Diabetes Mellitus in medical terms. In diabetes the blood sugar level abnormally gets high over a long period of time due to grouping of metabolic diseases. Due to high blood sugar patient complains the problem of frequent urination, increased hunger, and increased thirst. When the disease progresses, low amount of insulin is developed in the body which results in the less absorption of glucose by the cells. As a result blood glucose level is increased. When glucose is unabsorbed by the cells, it remains in the blood stream and kidneys needs to filter more glucose, but there is a limit to the amount of glucose kidney can filter. As a result more glucose is passed in the urine. Since glucose retains water, there will be increased urine which leads to the problem of frequent urination and excessive thirst. The main cause of diabetes is absence or insufficient production of insulin. Diabetic and nonketotic hyperosmolar coma can arise if the diabetes is not treated at early stage and also cause various long term complications like heart disease, stroke, kidney failure, foot ulcers and damage to the eyes. Diabetes is mainly of three types. Type 1 DM was previously known as insulindependent diabetes mellitus (IDDM) or juvenile diabetes and results from the insufficient or absence of insulin production by the body. This type of diabetes is partly inherited and sometimes triggered by viral infection or inappropriate diet. Type 1 DM is termed as “juvenile diabetes” because major cases of this type of diabetes are found in children. Most of the affected people on the onset of diabetes are healthy. Type 2 DM results from excessive body weight, inadequate exercise and begins with a condition in which cells do not respond to insulin properly and becomes less sensitive to insulin. This problem can be reversed with medication and variety of measures at the early stage of the disease. Gestational diabetes occurs in pregnant women when they develop high blood sugar level without previous history of diabetes. It resembles type 2 diabetes mellitus in many aspects like inadequate secretion of insulin and less responsiveness to insulin. This type of diabetes can also affect the health of mother and fetus if the diabetes is untreated. This type of diabetes is fully treatable, but requires care and medical supervision throughout the whole period of pregnancy.

• III.    Fuzzy Sets

Theory of sets is one of the important tools in modern mathematics. A set is a collection of similar type of distinct objects known as the element of the set. When some class is formed like “class of short men”, “class of tall men”, “class of high buildings”, “class of expensive cars” some kind of ambiguity, imprecision or vagueness arises in deciding whether an element belongs to a class or not. In such type of classes an object need not belong to a class there may be a degree of belongingness. There comes the concept of fuzzy sets which was introduced by Lotfi A. Zadeh. Fuzzy sets may be viewed as an extension of crisp sets as they allow the partial membership which is not possible in the crisp sets. The membership of an element in a fuzzy set does not require being complete, that is any element of a fuzzy set can also be member of some other fuzzy set in the same universe. Fuzzy sets are used to deal with the imprecison present in the data and most of the real world problems are vague, i.e., they are not sharply defined and precise problems. In fuzzy sets there are no sharp boundaries because there is some vagueness present in the data. The degree of membership for fuzzy sets is between 0 and 1. The fuzzy sets can be represented as:

р ( x ) : X ^ [ 0,1 ] (1)

where X denote a universal set, and for a crisp set µ A (x) is 1 or 0 as x either belongs or does not belongs to A. But when A is a fuzzy set then the value of µ_A (x) is between 0 and 1 and shows a partial membership. If the membership function for all the members under consideration is 1, then the fuzzy set is said to be universal fuzzy set or whole fuzzy set. For the implementation and use of fuzzy expert sysytem one needs to understand the concept of fuzzy sets and fuzzy logic [11].

• A.    Operations

There are various operations that we can apply on fuzzy sets.

• a.    Union

The union of fuzzy sets A and B is denoted by AUB and defined by:

pAuB( x) = max[pfe(x), рв(x)] for all x g U.(2)

• b.    Intersection

The intersection of fuzzy sets A and B is denoted by A ∩ B and defined by:

рлпв(x) = min[px), рв(x)] for all x g U.(3)

• c.    Complement

The complement of fuzzy sets A is denoted by Ā and defined by:

рл(x) = 1 - рл(x) for all x g U.(4)

• d.    Algebraic Sum

The algebraic sum (A+B) of fuzzy sets A and B is defined as:

• e.    Algebraic Product

The algebraic product (A • B) of two fuzzy sets A and B is defined as:

pA^ b(x) = pA(x) • pB(x).(6)

• f.    Bounded Sum

The bounded sum (A B) of two fuzzy sets A and B is defined as:

рлев(x) = min{1, Pa(x)+ рв(x)}.(7)

• g.    Bounded Difference

The bounded difference (A ʘ B) of two fuzzy sets A and B is defined as:

^лев(x) — max{0, ^л(x) — ^з(x)}.

• B.    Fuzzy Inference System(FIS)

Fuzzy Inference System provides a way of mapping input space to output space. Mapping provides a basis for decision making. The primary task of fuzzy inference system is decision making based on IF-THEN rules. Along with IF-THEN rules FIS uses “AND” or “OR” connectors for making necessary decisions. FIS is the key unit of a fuzzy logic system. Input to FIS need not be always fuzzy; it may be crisp or fuzzy, but the output is always a fuzzy set from the FIS. The process of fuzzification and defuzzification is of great importance in FIS. Fuzzy Inference System is also known as fuzzy expert system, fuzzy model and fuzzy rule-based system.

FIS consists of five functional blocks. They are:

• 1.    Fuzzification unit converts the crisp values into fuzzy values.

• 2.    Rule Base contains a number of fuzzy IF-THEN rules.

• 3.   Database defines the various  membership

• 4.   Decision-making unit performs  the  required

• 5.   Defuzzification unit converts the fuzzy sets into

functions of fuzzy sets used in fuzzy rules.

operations on the rules.

crisp set as a result.

In Fig.1 fuzzy inference system is shown in which the Fuzzifier converts the crisp input to a linguistic variable using the membership functions stored in the fuzzy knowledge base. After that using IF-THEN fuzzy rule, inference engine converts the fuzzy input to the fuzzy output. It uses the knowledge base which contains the membership functions for fuzzy sets used in the fuzzy rules. Then Defuzzifier converts the fuzzy output of the inference engine to crisp using membership functions analogous to the ones used by the Fuzzifier.

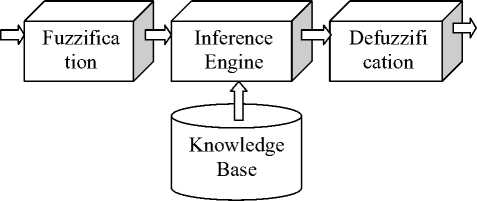
Fig.1. Fuzzy Inference System

There are mainly two types of FIS:

• 1.  Mamdani FIS

• 2.   Sugeno FIS

• a.    Mamdani FIS

  Mamdani's fuzzy inference system is the most common fuzzy methodology. Mamdani's method was the first control system that was built using fuzzy set theory. It was proposed by Ebrahim Mamdani in 1975 as an attempt to control a combination of steam engine and boiler by synthesizing a set of linguistic control rules that are obtained from experienced human operators. Mamdani's effort was based on Lotfi Zadeh's 1973 work on fuzzy algorithms for decision processes and complex systems [12]. Mamdani method uses the process of aggregation after the generation of fuzzy output to aggregate the multiple output membership functions to generate a single output membership function.

• b.    Sugeno FIS

  Sugeno, or Takagi-Sugeno-Kang, method of fuzzy inference was introduced in 1985. This method is similar to the Mamdani method. The first two parts of the fuzzy inference process i.e. fuzzifying the inputs and applying the fuzzy operator are same. The main difference between Sugeno and Mamdani model is that the output membership functions of Sugeno are either linear or constant and the parameters of Sugeno FIS are more adjustable than the Mamdani method [12].

This paper uses the Mamdani inference system due to its simplicity and its widespread acceptance. It is also well-suited for human input. In Mamdani model fuzzy rules are formed using IF-THEN statements and AND/OR connectives. Then one fuzzy output distribution is obtained by combining all the fuzzy rules.

• IV.    Related Work

  M. Kalpana and Dr. A.V Senthil Kumar [1] developed a fuzzy expert system that was based on the concepts of fuzzy logic, using fuzzy verdict mechanism for the diagnosis of diabetes by analyzing the data of the patients and compared the result of the expert system with the previous available mechanisms in the year 2011. In 2013 Nicole Sprunk, Alejandro Mendoza Garcia, Robert Bauernschmitt and Alois Knoll [2] evaluated an adaptive algorithm for fuzzy type-2 controller that incorporated the knowledge of several physicians for the application of blood pressure regulation with the help of fuzzy logic. In the paper, firstly type-2 fuzzy controller was introduced and in the second step an adaptive algorithm was developed then the result of both type-2 fuzzy controller and adaptive algorithm was compared.

In the year 2013 Ashish Patel, Shailendra K Gupta, Qamar Rehman and M. K. Verma [3] presented some general ideas of the fuzzy logic and their application in the various fields of biomedical informatics like fuzzy logic in the ventilated newborn infants for the control of inspired oxygen, anesthetics, bioinformatics, and medicine. In the year 2011, Chang-Shing Lee [4] designed a fuzzy expert system based on the fuzzy ontology for diabetes decision support application with five layer fuzzy ontology. Manoranjan Kumar Singh, L. Rakesh and Aniket Ranjan [5] evaluate the risk of drug addiction and provide a general view of application of fuzzy logic using fuzzy sets and a basic summary of the techniques used in solving the practical problems related to health. They also illustrate the risk associated with smoking and alcohol drinking in 2010.

In 2009 Songhua Xie, Dehua Li and Hui Nie [6] have described the process of innovative formulations in Chinese medicine and using fuzzy clustering and put forward the method of single drug optimization selection based on Possibility Construction Space Theory (PCST) because Chinese medicines are based on the large number of fuzzy concepts. In the year 2006, Angela Torres and Juan J. Nieto [7] have presented the role of fuzzy sets in fuzzy hypercube for the development of medicine and in the field of bioinformatics. They presented the two concrete illustrations of drug addiction and comparison of genomes using fuzzy logic in the paper. In 2006, L. B. Goncalves, M. M. B. R. Vellasco, M. A. C. Pacheco, and F. J. de Souza [8] introduced an inverted hierarchical neuro-fuzzy BSP system for rule extraction and pattern classification in databases. Klaus-Peter Adlassnig [9] demonstrated the importance and role of knowledge base decision support fuzzy system in medicine, weaning from artificial ventilation, patient monitoring, toxoplasmosis laboratory, therapeutic decision support and their efficiency in the field of medical.

• V.    Proposed Fuzzy logic based Diabetes Diagnosis system (FLDDS)

This section describes the architecture of proposed fuzzy expert system (FLDDS), fuzzy verdict mechanism, and a proposed algorithm used in this paper. In the following architecture of the fuzzy expert system the information of PIDD is transferred into the required knowledge for the diagnosis of diabetes using the concepts of fuzzy logic.

• A.    Architecture of Fuzzy Logic Based Diabetes Diagnosis System (FLDDS)

The proposed framework follows various steps shown in Fig.2.

• a.    Collect Patient Details

This is the first step of proposed fuzzy expert system. Here the input parameters are taken from the patients based on the common symptoms of diabetes that include their blood glucose level, age, gender, background information about family, body mass index, frequency of urination, thirst level, insulin, hunger rate, gestational information, poor wound healing, food habit, blood pressure etc. After that all the collected information is stored in the database for the analysis purpose. In this paper we have used Pima Indians Diabetes Database which is discussed in section B.

• b.    Analyse & Select the Input Parameter

Once the first step has been completed it directs to the next step of analyzing and normalizing the input parameter in which we analyze all the input parameters given by the patient and select the input parameters which play important role in the mechanism of diabetes diagnosis based on the experts knowledge.

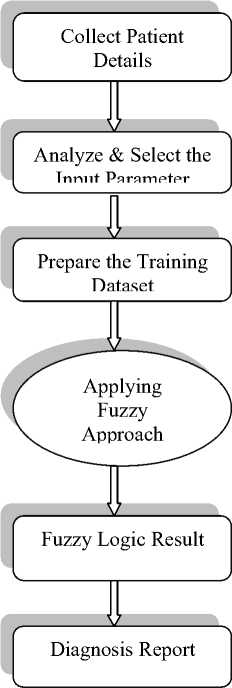
Fig.2. Architecture of FLDDS

c. Prepare the Training Dataset

Table 1. Parameters of Triangular Membership Functions

Fuzzy Input Variables	Linguistic Variables	Fuzzy Triangular numbers
Glucose	Low	[56 100 125]
	Medium	[68.2 117 145]
	high	[109.9 146 198]
INS	Low	[0 55.11 87.67]
	Medium	[63.63 98.42 191.6]
	high	[95.34 188.3 586]
BMI	Low	[18 22 30.8]
	Medium	[31.01 37.01 45.01]
	high	[36.43 44.43 67]
DPF	Low	[0.085 0.5322 1.132]
	Medium	[0.547 1.03 1.717]
	high	[1.09 1.476 2.4]
Age	Young	[25 25 26]
	Medium	[25 26 27]
	Old	[26 27 30]
Urine	Low	[0.5 50 800]
	Medium	[500 1300 2000]
	high	[1500 2500 5000]
DM	Very Low	[0 0.1 0.2]
	Low	[0.1524 0.2524 0.3]
	Medium	[0.287 0.3333 0.3997]
	High	[0.355 0.623 0.762]
	Very High	[0.731 0.831 1]

After selecting the input parameter, the next step is to prepare the training dataset. The prepared dataset will act as input for the fuzzy rule-based system to train the system for the diagnosis of diabetes and generate the result. The datasets used in this paper is shown in the Table 1.

• d.    Fuzzy Approach

This is one of the main steps of the proposed system. In which we apply the fuzzy approach that is fuzzy verdict mechanism discussed in section C. using the Mamdani FIS to diagnose the diabetes. Firstly, crisp values are converted into fuzzy values using fuzzification and given as input to the fuzzy inference system for applying rule base algorithms to generate the result based on the knowledge of the human experts.

• e.    Fuzzy Logic Result

This step involves the generation of fuzzy logic result. In this step we analyze the fuzzy result and convert the fuzzy result into the crisp result by applying the defuzzification mechanism.

• f.    Diagnosis Report

This is the final step of the proposed system. The expected generated report shows the efficiency and the accuracy of the prediction rate of the diabetes diagnosis.

• B.    Dataset (Pima Indians Diabetes Database)

In this work, we have used the dataset of Pima Indians Diabetes Database. Pima Indians is a group which has the highest rate of diabetes worldwide. The National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) [10] have examined the Pima Indians. And the database of PIMA Indians is retrieved from the Internet .

• C.    Fuzzy Verdict Mechanism

Fuzzy Verdict Mechanism constructs large knowledge base system for diabetes diagnosis. For each instance in fuzzification all the possibilities of developing diabetes by an individual is interpreted by fuzzy verdict mechanism and after performing the fuzzification all the

Possibilities are converted into sentences. By using the fuzzification, the system converts the crisp value into fuzzy value to construct the knowledge base. Fuzzy Verdict Mechanism uses the triangular membership function using the Mamdani’s inference. After applying all the IF-THEN rules in fuzzy inference system the fuzzy values are converted to the crisp values using defuzzification technique to produce the result [13], [14]. In the previous work, researchers have considered the glucose, insulin (INS), body mass index (BMI), Age, diabetes pedigree function (DPF), diabetes mellitus (DM) parameters. But according to our study and physicians, polyuria also plays an important role in the diagnosis of diabetes. Hence, in this paper glucose, INS, BMI, DPF, age and urine is taken as fuzzy input variables and the DM as output variable as shown in Fig.3.

Table 1 shows the parameters of fuzzy numbers taken as input to the inference system.

In Table 1 fuzzy variable Glucose is having three fuzzy numbers, i.e., GlucoseLow, GlucoseMedium and GlucoseHigh. Another fuzzy variable INS uses three fuzzy numbers INSLow, INSMedium and INSHigh. BMI fuzzy variable is also using three fuzzy numbers that are BMILow, BMIMedium and BMIHigh. For the fuzzy variable DPF DPFLow, DPFMedium and DPFHigh fuzzy numbers are used. The membership function of Age fuzzy variable has three fuzzy numbers AgeYoung, AgeMedium and AgeOld. Urine is taken as another important fuzzy input variable having UrineLow UrineMedium and UrineHigh and the DM as fuzzy output variable having five fuzzy numbers DMVerylow, DMLow, DMMedium, DMHigh and DMVeryhigh.

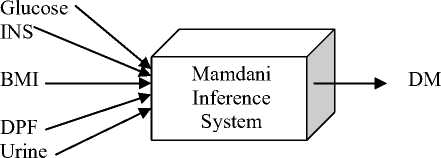
Fig.3. Fuzzy Verdict Mechanism

Fig.4. shows the membership graphic for the urine fuzzy variable with three fuzzy numbers low, medium and high.

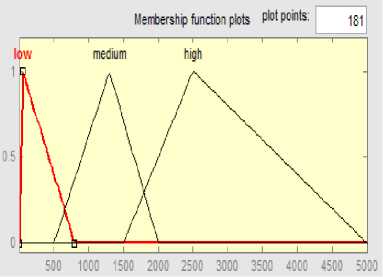
Fig.4. Membership graphic diagram of fuzzy variable urine with its three fuzzy numbers

Fig.5. shows the control surface of the DM fuzzy variable for the proposed fuzzy expert system over the two fuzzy input variable urine and glucose.

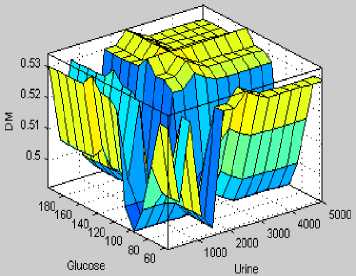
Fig.5. Control surface for fuzzy expert system over two input.

• D.    Proposed Algorithm (FLDDA):

The proposed algorithm consists of following six steps:

INPUT

Fuzzy set of glucose, INS, BMI, DPF, age and urine are taken as input.

OUTPUT

Fuzzy set DM.

STEPS

Step 1: Input crisp values of glucose, INS, BMI, DPF, age and urine.

Step 2: Set the triangular membership function for the fuzzy number.

Step 3: Build the fuzzy numbers for glucose, INS, BMI, DPF, age and urine for input set & output set DM.

Step 4: Execute Mamdani’s Fuzzy inference method.

Step 4.1: Input the rules and calculate the matching degree of rule with ‘OR’ fuzzy disjunction for fuzzy input set (Glucoselow, Glucosemedium, Glucosehigh, INSlow, INSmedium, INShigh, BMIlow, BMImedium, BMIhigh, DPFlow, DPFmedium, DPFhigh, Ageyoung, Agemedium, Ageold, Urinelow, Urinemedium, Urinehigh).

Step 4.2: Calculate the aggregation of the fired rules for fuzzy output set DM (DMverylow, DMlow, DMmedium, DMhigh, DMveryhigh).

Step 5: Defuzzify into the crisp values by:

z * =

J Ц А ( z ) • zdz J Ц А ( z ) dz

where, ∫ denotes algebraic integration, µ A (z) means the number of fuzzy numbers of the output fuzzy variable DM and z represents the weight for µ A (z).

Step 6: Present the knowledge in the form of human nature language.

END.

• E.    Description of Output

The output of the following experiment is represented in the form of decision sentence.

• a.    Sentence Analysis

Sentence Analysis represents the physical data of the person as glucose level of person [Fuzzy Number(Glucose):    Glucoselow,    Glucosemedium,

Glucosehigh], insulin is [Fuzzy Number(INS): INSlow, INSmedium, INShigh], body mass index is [Fuzzy Number(BMI):  BMIlow, BMImedium, BMIhigh], diabetes pedigree function is [Fuzzy Number(DPF): DPFlow, DPFmedium, DPFhigh], at age[Fuzzy Number(Age): Ageyoung, Agemedium, Ageold] and volume of urine is [Fuzzy Number(Urine): Urinelow, Urinemedium, Urinehigh]

• b.    Decision Sentence

Decision sentence is used to describe the possibility or the chances of a person suffering from diabetes as:

[Fuzzy Number (DM):  DMVerylow, DMlow,

DMmedium, DMhigh, DMveryhigh]

Possibility: [0, 1].

Where in possibility, 0 indicates that person is nondiabetic and 1 indicates that person is diabetic patient.

• VI.    Experimental Results

The proposed fuzzy expert system is implemented with the MATLAB [15]. Table 2 shows the result obtained from the experiment.

Table 2. Result obtained from MATLAB

Physical Data	Glucose (mg/dl)	INS (mu U/m l)	BMI (kg/ m²)	DPF	Age	Urine (ml/da y)
	78	88	31	0.248	26	100
Sentence Analysis	If (Glucose is low) or (INS is low) or (BMI is low) or (DPF is low) or (Age is young) or (Urine is low) then (DM is verylow)
Decision Sentence	The Decision sentence justifies that the possibility of suffering from diabetes for this person is medium (possibility:0.293)
Medical Practitioner Justification	Medical practitioner justification is the person is Non-diabetic.

The obtained result indicates that the proposed approach supports analysis of physical data. The proposed approach can analyze the data by considering more parameters and based on that it generates the result with more accuracy.

• A.    Rules for Fuzzy System

The following six rules are used in this experiment using OR connectives for the purpose of diabetes diagnosis.

• 1.    If (Glucose is low) or (INS is low) or (BMI is low) or (DPF is low) or (Age is young) or (Urine is low) then (DM is verylow)

• 2.    If (Glucose is low) or (INS is low) or (BMI is high) or (DPF is low) or (Age is young) or (Urine is medium) then (DM is Low)

• 3.    If (Glucose is medium) or (INS is high) or (BMI is high) or (DPF is medium) or (Age is young) or (Urine is medium) then (DM is medium)

• 4.    If (Glucose is high) or (INS is medium) or (BMI is high) or (DPF is high) or (Age is young) or (Urine is high) then (DM is high)

• 5.    If (Glucose is low) or (INS is low) or (BMI is medium) or (DPF is low) or (Age is young) or (Urine is medium) then (DM is verylow)

• 6.    If (Glucose is high) or (INS is high) or (BMI is high) or (DPF is high) or (Age is old) or (Urine is high) then (DM is veryhigh)

• B.    Evaluation of Accuracy

This experiment is performed for the evaluation of system performance based on the Decision sentence and the Medical practitioner. Accuracy acts as a measuring scale in any experiment to measure the performance of the system. Therefore the evaluation of the accuracy in this experiment is very important. Here, accuracy is defined as the proportion of total number of predictions that were correct with the total number of number of all the predictions. The formula for accuracy is given in eqn. (8).

Accuracy =

TN + TP

TN + FP + FN + TP x 100%

Table 4 shows the comparison of our proposed system with the previously available six systems.

Table 3. Outcomes of Two-Class Prediction

Actual Class	Predicted Class
	Yes	No
Yes	True Positive(TP)	False Negative(FN)
No	False Positive(FP)	True Negative(TN)

Table 4. Comparison of proposed system accuracy with the earlier systems

Method	Accuracy (%)	Author
FLDDS for Very Young	87.2	Vaishali Jain, SupriyaRaheja
FVM for Diabetes Decision Very Young	85.03	M.Kalpana, A.V Senthil Kumar
FES	81.7	Lee and Wang
HNFB-1	78.26	Goncalves et al.
Logdisc	77.7	Statlog
IncNet	77.6	Norbert Jankowski
DIPOL 92	77.6	Statlog

Accuracy (%)

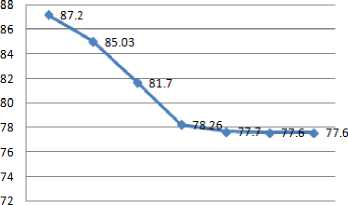
very FVM FES HNFB-1 Logdisc IncNet DIPOL young                                    92

Fig.6. Graphical representation of accuracy

The final experiment compares the accuracy of proposed system with the previously proposed methods and it is shown in the Table 4 and Fig.4.

The experimental result in Table 4 and Fig.4 proves that the proposed system performs better and more accurate as compare to previous systems based on the finding for the accuracy of a system. The above result shows that accuracy of proposed system is better than the previous available systems which come out to be 87.2%.

• VII.    Conclusion

This paper illustrates the use of fuzzy verdict mechanism in Fuzzy Logic based Diabetes Diagnosis System (FLDDS) which is used for the diagnosis of diabetes. Initially experimental datasets are processed into crisp values and then the crisp values are converted into fuzzy values in the fuzzification stage. Then fuzzy verdict mechanism executes the rules to make the decision on possibility of whether an individual is suffering from diabetes or not and provides the description of result. The proposed method indicates that their performance is increased with the increase number of considerable and important parameters and gives the result with more accuracy. This research proves the importance of urine parameter for the diabetes diagnosis and shows the accuracy of the mechanism is improved after taking this parameter into the consideration.

• [1]    M.Kalpana and Dr. A.V Senthil Kumar, “Fuzzy Expert System for Diabetes using Fuzzy Verdict Mechanism”, International Journal Advanced Networking and Applications Volume: 03, Issue: 02, pp 1128-1134, 2011.

• [2]    Nicole Sprunk, Alejandro Mendoza Garcia, Robert Bauernschmitt and Alois Knoll, “Evaluation of an adaptive algorithm for fuzzy type-2 control in blood pressure regulation”, IEEE International Conference on Fuzzy Systems, Hyderabad, India, July 07-10, 2013, Proceedings., pp 1-5, 2013.

• [3]    Ashish Patel, Shailendra K Gupta, Qamar Rehman and M. K. Verma, “Application of Fuzzy Logic in Biomedical Informatics”, Journal of Emerging Trends in Computing and Information Sciences , pp 57-62, 2013.

• [4]    Chang-Shing Lee, “A Fuzzy Expert System for Diabetes Decision Support Application”. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics , vol. 41, no. 1, Feb. 2011.

• [5]    Manoranjan Kumar Singh, L. Rakesh and Aniket Ranjan (2010),“Evaluation of the Risk of Drug Addiction with the Help of Fuzzy Sets”, Journal of Applied Computer Science & Mathematics, no. 9 (4) /2010, Suceava , pp 98-103, 2010.

• [6]    Songhua Xie, Dehua Li and Hui Nie, “Research on the Selection of Innovation Compound Using Possibility Construction Space Theory and Fuzzy Clustering”, 2009 Second International Conference on Intelligent Computation Technology and Automation, pp 788-791, 2009.

• [7]    Angela Torres and Juan J. Nieto, “Fuzzy Logic in Medicine and Bioinformatics”, Journal of Biomedicine and Bioinformatics, 2006.

• [8]    L. B. Goncalves, M. M. B. R. Vellasco, M. A. C.Pacheco, and F. J. de Souza, “Inverted hierarchical neuro-fuzzy BSP

system:  A novel neuro-fuzzy model for pattern classification and rule extraction in databases”, IEEE Transactions on Systems, Man, and Cybernetics-Part C: Application and Reviews, vol. 36, no. 2, pp 236-248, March 2006.

• [9]    Klaus-Peter Adlassnig, “Fuzzy Systems in Medicine” Conference Proceedings of the 2nd International Conference in Fuzzy Logic and Technology, Leicester, United Kingdom, pp 2-5, September 5-7, 2001.

• [10]    J. Demouy, J. Chamberlain, M. Harris, and L. H. Marchand, “The Pima Indians: Pathfinders of Health”. Bethesda, MD: Nat. Inst. Diabetes Digestive Kidney Diseases, 1995.

• [11]     http://en.wikipedia.org/wiki/Fuzzy_logic .

• [12]     http://in.mathworks.com/help/fuzzy/types-of-fuzzy-inference-systems.html .

• [13]    M. Margaliot, “Bio mimicry and fuzzy modelling: A match made in heaven”, IEEE Computational Intelligence Magazine, vol. 3, no. 3, pp. 38-48, August 2008.

• [14]    L. A. Zadeh, “Toward human level machine intelligence. Is it achievable? The need for a paradigm shift”, IEEE Computational Intelligence Magazine, vol. 3, no. 3, pp. 1122, Aug. 2008.

• [15]     http://in.mathworks.com/products/matlab/ .

• [16]    C. S. Lee and M. H. Wang, “Ontology-based intelligent healthcare agent and its application to respiratory waveform recognition”, Expert System Application, vol. 33, no. 3, pp. 606-619, Oct. 2007.