Individually Directional Evolutionary Algorithm for Solving Global Optimization Problems-Comparative Study

Published Online August 2015 in MECS

Evolutionary algorithms (EAs) are a class of probabilistic optimization techniques inspired by natural evolution process, witch belong to methods of computational intelligence (CI). Classical optimization methods require that the objective function have some properties such as continuity or are differentiable. These requirements make use of conventional methods of optimization for real-world problems difficult or impossible. Limited applicability of classical optimization methods influence the popularization of stochastic optimization techniques [1,10]. Optimization algorithms such as EAs are used in artificial intelligence (AI) to optimize the structure of neural networks [6, 15] or adapt the weights for fuzzy cognitive map [11 - 13].

EAs includes techniques such as genetic algorithms (GA), evolution strategies (ES), evolutionary programming (EP) and genetic programming (PG). All these techniques have been developed in different research centers. Common name helps to avoid problems with classification of new optimization techniques similar to more than one technique of EAs. Evolutionary Computing (EC) is other common name for EA.

Popularity of EAs has led to a many of modifications of them [2, 8]. These modifications can be divided into several groups: modifications based on intermixing techniques of EAs, modifications independent from representation of solutions and modifications designed to solve specific problem or group of problems. The first group includes modifications such as adding a genetic operator known as a crossover, developed for GA, to ES or using a floating-point representation in GA, known from ES. The second group of modifications contains elements algorithm used by EAs such as alternative selection methods - tournament selection, rank based selection or threshold selection. Specific encoding scheme and genetic operators are in last group of modifications. EAs together with other modifications from the last group are applied to solve travelling salesman problem. These EAs use integer based encoding scheme and genetic operators, that are processing this encoding scheme.

EAs are based on concepts of natural selection and natural genetics. The basic principle of EA is searching optimal solution by processing population of individuals. This process leads to increasing the average value of fitness function of the population in subsequent cycles of the algorithm. Selection methods and genetic operators allow to choose individuals, which represent better solution and exchange information among each other. Selection methods are similar to the natural evolution process and genetic operators are similar to the reproduction of individuals in natural environment. The newly created individuals represent new solutions. Better rated solutions have more chance to transition to the next population. Elite selection methods allow to accelerate the convergence of algorithm. Elite scheme allows the survival of the fittest individuals.

EAs attempt to imitate the process of evolution described by Darwin. The process of function optimization is reduced to the adaptation of a species to the natural environment in successive generations. Improving the value of average fitness function of the population is realized by selection methods and genetic operators. This process assumes that indirectly created worse solutions can lead to a better final solution. Subsequent created populations contain the majority of newly created individuals, that prevents monitoring of the evolution of each individual.

IDEA is a newly developed algorithm for global optimization. Main principle of IDEA is to monitor and direct the evolution of selected individuals of population to explore promising areas in the search space. The algorithm uses a proportional selection method with dynamic linear scaling of fitness function and nonuniform mutation uses information about the direction of change also known as direction vector. Applied selection method and mutation operator in IDEA allows to choose the fittest individuals and their modification to explore promising areas in the search space. The idea of IDEA is an independent evolution of individuals in current population. An independent evolution process is focused on indicating correct direction of changes in the elements of solution vector.

The paper is organized as follows. Section 2 contain information about mutation operators applied in EAs. This information relates mainly to the directed mutation operators. Section 3 is description of designed algorithm IDEA. The set of benchmark problems, the compared algorithms and the results of simulation analysis are reported in Section 4. Finally, Section 5 presents a number of conclusions from the present study.

• II.    Related Work

Classical mutation operator used in the binary coded genetic algorithm (BCGA) is changes randomly selected bits of binary string, that represent each individual. Similar technique is used for RCGA - selected digits of each element of the solution vector randomly changes. However, RCGA allows the use of more sophisticated techniques to modify the current solution than random mutation. Common random mutation operators for RCGA are non-uniform mutation (NUM), uniform mutation (also known as random mutation), power mutation (PM) or boundary mutation (BM).

These operators are purely random - the change of each element is performed independently of previous or other changes. Another type of mutation operators are directional mutation operators (DMO). These operators take into account the impact of mutation on fitness function of individuals. Pointed Directed (PoD) [3] Mutation requires to complement representation of solution by binary direction vector (DV) for each individual. This vector contains a single bit for each gene, which dictates the direction of mutation. The DV is corrected by feedback from the current population. PoD has been modified and named mutation-with-momentum [4]. The mutation-with-momentum algorithm requires additional data to be stored for each gene in an individual's genetic representation. These additional data represent a change of gene value in most recent mutation. The directional mutation operator proposed in [7] is based on distribution of individuals over intervals of each dimension. The statistics information is used to direct the mutation of an individual toward the neighboring interval. Another example of a directional mutation is a mutation based on the α-stable distributions [9]. Adaptive directed mutation (ADM)[14] uses the impact of change values of the solutions vector to value of fitness function of each individual in subsequent generations.

This paper suggest the use of directional non-uniform mutation operator (DNUM). DNUM is similar to NUM operator [8] but direction vector is used to modify individual genes. As a result of DNUM work, a single gene of an individual has been modified in accordance with the direction vector. This technique allows to explore the search space in accordance with direction that produced a better solution in previous generations. In the case when the mutation has not led to the creation of better solution, the corresponding value of DV is adjusted.

• III.    Individually Directional Evolutionary Algorithm

Individually directional evolutionary algorithm (IDEA) uses characteristic elements of EAs such as proportionate selection (roulette-wheel selection) with dynamic linear scaling of fitness function in pre-selection stage, directional non-uniform mutation operator (DNUM) as genetic operator and elite scheme in post-selection stage. Figure 1 shows the scheme of IDEA.

procedure IDEA begin

t:=0

initialization P0

evaluation P0

Pt:=P0

while (not stop condition) do begin

Tt:=pre-selction Pt

T’t:= directional non-uniform mutation Tt evaluation T’t

Pt+1:=post-selection (T’t, Tt)

t:=t+1

end end

Fig. 1. IDEA scheme.

Evolution loop of IDEA is initialized in the same way as in other EAs and is made up of 4 steps. In the first step, temporary population T is created from current base population P. Individuals of population T will be subject to mutation. In the second step, another temporary population T' is created by mutations of individuals of temporary population T. Individuals of temporary population T' are evaluated in third step of evolution loop. The last step of evolution loop is to select individuals from temporary population T and T', that will create the next base population P.

• A.    Solution encoding

The developed algorithm IDEA uses solution encoding similar to algorithms such as RCGA or ES expanded by the additional direction vector (DV). Each individual is represented by two n-dimensional vectors (1).

O =< X , D >                              (1)

where:

X = [ x 1 , x 2 , x 3 ,..., x n ],

D = [d 1, d2, d3,..., dn ], x e Rn, i = 1,2,3,..., n , dt e {-1,1}, i = 1,2,3,..., n .

The vector X represents a potential problem solution. The vector D contains information about mutation direction. This vector is used in the mutation operation.

• B.    Pre-selection process

Pre-selection procedure used by IDEA is a classic mechanism of proportionate selection with dynamic linear scaling of fitness function [5]. The value of the fitness function is decreased by the value of f ^t (2).

.t _/ 0.99 • f ™ f or f ^ > °            _m

• ^У°   1 1-01 • ff or f < °

where: f ^t - fitness function value of “the worst” individual of population P^t.

The accepted method of calculating the value of f ^t allows obtain a non-zero probability of select the worst individual from population.

• C.    Directional non-uniform mutation

Directional non-uniform mutation operator is a modified non-uniform mutation operator [8]. In the case of DNUM, the mutation of selected gene is carried out in accordance with the value of corresponding element of directional vector (3).

• x , -A ( t , x,. - L ) for d =- 1

y« = 1 ^{1        11}        i               (3)

[ x _;. + A ( t , u_t - x _;.) for d_t = 1

d - mutation direction of the i-th gene of the individual, x - current value of the i-th gene of the individual, y - new value of the i-th gene of the individual.

In effect of DNUM is one and only one element of solution vector of any individual that has been modified. This allows to correct the direction of mutation of any gene for each individual in the post-selection process.

• D.    Post-selection process

Post-selection process is similar to the greedy selection [17,18]. In greedy selection, the new better individual replaces the current worse individual. New individuals are created by the mutation of following genes. In postselection process, the individual of temporary population T is compared to the corresponding individual from temporary population T'. The corresponding individual from temporary population T' was created by the mutation the individual from temporary population T. Each individual of population T has one and only one corresponding individual in temporary population T'. The difference between these individuals is only the one mutated gene value. One of these individuals, (better rated) is selected for the next base population. If the mutated individual is worse than the corresponding individual, the corresponding element of directional vector of the primary individual will be corrected. The value of the corresponding element of directional vector is corrected by multiplying this value by -1 (4).

d i = d i- ( — 1)                                       (4)

d - mutation direction of the i-th gene of the individual.

This process is called the process of correction of mutation direction and allows to change values of solution vector according to the direction, which previously produced good results.

• IV. Simulation Analysis -Comparative Study

The subject of simulation analysis is a global optimization of selected multidimensional benchmark functions by selected EAs.

A typical nonlinear global optimization problem is defined as (5).

min f (x), were x e S and S e Rn.        (5)

max

The S is the search space. The problem is find value of x * from S , which minimizes/maximizes f ( x ) . The x * must comply with the conditions (6) for minimizing or maximizing f ( x ) .

min f (x) : f (x*) < f (x) for Vx e S max f (x) : f (x*) > f (x) for Vx e S

Problem of minimizing f ( x ) can be transformed into a maximizing f ( x ) (7).

x * = argmin( f ( x )) = argmax( - f ( x ))      (7)

x e S                  x e S

The developed algorithm IDEA was compared with other existing algorithms. The number of objective function value calculation is equal for all algorithms. This allows to compare the performance of the algorithms not considering the execution time, programing languages or hardware configuration. Although the calculation of value for benchmark functions is not time-consuming, it can be in the case of real-life problems.

• A.    Simulation settings

All compared algorithms use the same parameter values or equivalent values for specific parameters for some algorithm. Basic parameters of the algorithms shall adopt commonly used value [2, 8]. The comparative study contains the comparison of the following algorithms: developed algorithm IDEA, RCGA, elite RCGA with the one elite individual, elite RCGA with the number of elite individuals equal to population size and IDEA without directional vector – scheme of this algorithm is the same as in IDEA but uses mutation operator NUM instead of DNUM. Elite RCGA with the number of elite individuals equal to population size is similar to ES ( Ц + X ) with crossover operator [2]. RCGA and both elite RCGA use uniform crossover operator with exchange probability ( p ) equal to 0.5 and crossing probability ( p ) equal to 0.75. RCGA and both elite RCGA use NUM with mutation probability ( p ) equal to 0.03. The adopted value of p is equivalent to “mutation probability” of DNUM used by IDEA, where a single gene is mutated for any individual of population in each algorithm cycle. All these algorithms use a proportionate selection with dynamic linear scaling of fitness function described in section 2. The size of the population and the number of generations are the same for all algorithms. Their values are respectively 100 individuals and 2000 generations.

• B.    Benchmark functions

The benchmark functions are given in Table 1. Unimodal functions f - f are called: Sphere Model, Schwefel’s Problem 2.22, Schwefel’s Problem 2.21, Generalized Rosenbrock’s Function. Function f is the step function, which has one minimum and is discontinuous. Function f is a noisy quartic function, where random[0, 1) is a uniformly distributed random variable in [0, 1). Multimodal functions are f – f and are called: Generalized Rastrigin’s Function, Ackley’s Function and Generalized Griewank Function.

Table 1. Benchmark functions [8, 16].
fi	xi	f min
30 fк x ) = E x-2 i = 1	xt G [ - 100,100], i = 1,2,...,30	f min (0,0,...,0) = 0
30           30 f 2( x) = E i x - 1 +П i x - 1 i = 1               i = 1	x , G [ - 10,10], i = 1,2,...,30	f mh (0,0,...,0) = 0
f 3( x ) = max - {| x i 1,1 <  - <  30}	xt g [ - 100,100], i = 1,2,...,30	f min (0,0,...,0) = 0
f 4 ( x ) = f>0( x w - x , 2)2 + ( x , - 1)2] i = 1	xz. g [ - 30,30], i = 1,2,...,30	f m„ (1,1,...,1) = 0
30 f 5 ( X ) = £ ( L x, + 0.5 J )2 i = 1	xt g [ - 100,100], i = 1,2,...,30	f min (0,0,...,0) = 0
30 f ( x ) = E ix 4 + random^0,1) i = 1	x, g [ - 1.28,1.28], i = 1,2,...,30	f mh (0,0,...,0) = 0
f 7 ( x ) = £ ( x f - 10 cos(2 n x , ) + 10 i = 1	xt g [ - 5.12,5.12], i = 1,2,...,30	f min (0,0,...,0) = 0
1    30 f 8 ( x ) = - 20 exp( - 0.2     £ x i ) 30 i = 1 1   30 - exp(   E cos(2 n x 2)) + 20 + e 30 i = 1	xz. g [ - 32,32, i = 1,2,...,30	f mh (0,0,...,0) = 0
30         30 f ( x ) =   — T x 2 -    cos() + 1 9      4000 ^= 1 1    = 1      V ?	x;. g [ - 600,600], i = 1,2,...,30	f min (0,0,...,0) = 0
C. Experimental Results and Analysis Tables 2-4 present the results of optimization multidimensional functions. These tables show obtained value	of the best, the worst and average as a result of multiple launches of compared algorithms.

Based on simulation results (Tab. 2-4) it can be observed that the IDEA gives better results in comparison with other EAs. The best, worst and average result of optimization of benchmark functions is equal or better compared to other EAs for the wide range of selected benchmark functions. Comparison of the results obtained by IDEA and IDEA without vector of direction shows that the use of only IDEA scheme of post-selection does not provide obtain better results than elite RCGA with number of elite individuals equal to population size. The comparison of the worst results obtained by the algorithms shows that in most cases they are better for IDEA, which is confirmed by the average results of the optimization of benchmark functions.

Table 2. The best results achieved.

Function	f min	RCGA	Elite RCGA	Elite RCGA	IDEA without vector of direction	IDEA
f 1	0	137,6195	39,34134	0,04354	0,077377	0,016064
f 2	0	2,036238	1,281487	0,103552	0,091704	0,047126
f 3	0	1,797428	0,654677	0,090355	0,177037	0,098044
f 4	0	40659,75	4381,31	82,05972	41,332169	12,37685
f 5	0	144	38	0	0	0
f 6	0	0,284131	0,479216	0,932808	0,819021	0,102025
f 7	0	27,07454	4,841767	0,024082	0,052699	0,006697
f 8	0	3,500655	0,898639	0,055616	0,066552	0,030753
f 9	0	2,50413	1,424007	0,073187	0,417053	0,028646
			Table 3.	The worst results achieved.
Function	f min	RCGA	Elite RCGA	Elite RCGA	IDEA without vector of direction	IDEA
f 1	0	254,5255	75,07664	0,129015	0,178441	0,036108
f 2	0	3,514146	1,605774	0,168645	0,190154	0,084795
f 3	0	3,346235	1,060122	0,224434	0,550799	0,257424
f 4	0	101062,9	10915,08	193,0529	193,6963	105,1899
f 5	0	296	99	0	0	0
f 6	0	0,918662	0,304626	0,385808	0,257063	0,761903
f 7	0	32,97223	9,029178	0,062866	0,112555	0,014407
f 8	0	4,438607	1,699093	0,135306	0,15737	0,049317
f 9	0	3,819432	1,724608	0,170535	1,018339	0,178701
Table 4. The average results achieved.
Function	min	RCGA	Elite RCGA	Elite RCGA	IDEA without vector of direction	IDEA

f 1	0	205,4934	63,29672	0,072157	0,136031	0,023187
f 2	0	2,864105	1,469042	0,124475	0,143451	0,059191
f 3	0	2,658306	0,840783	0,134747	0,30542	0,145462
f 4	0	70978,62	7443,365	123,236	125,9332	78,63267
f 5	0	222,1	58	0	0	0
f 6	0	0,550015	0,545784	0,619994	0,559118	0,442814
f 7	0	29,37537	7,165922	0,035986	0,078663	0,011218
f 8	0	3,990445	1,343896	0,080027	0,106285	0,038786
f 9	0	2,934898	1,515274	0,12185	0,727247	0,089973

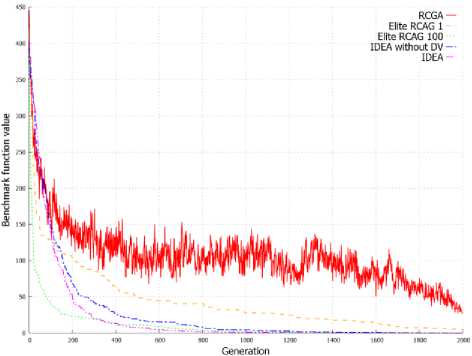
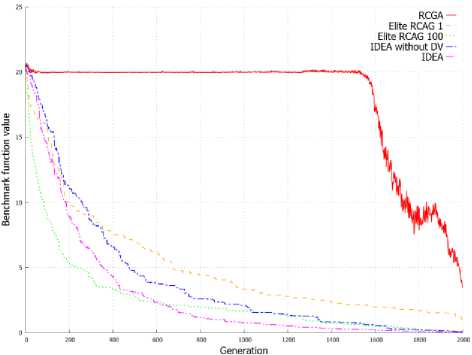
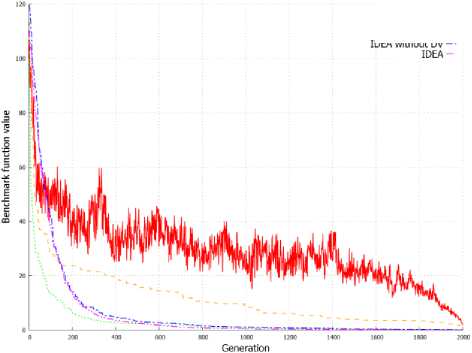
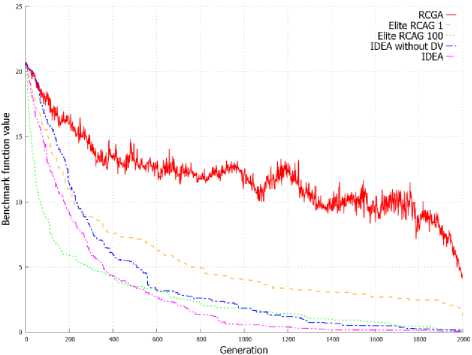
Figure 2. shows the value of benchmark functions for solution represented by the best individual in the subsequent generations. On the basis on graphs from Figure 2 it can be stated that the elite RCGA with number of elite individuals equal to population size achieve better result in initial cycles of algorithm. After few cycles, the IDEA achieves better solution than other EAs and finally returns the best solution in most of these cases. This is clearly visible in Figure 2d and 2e.

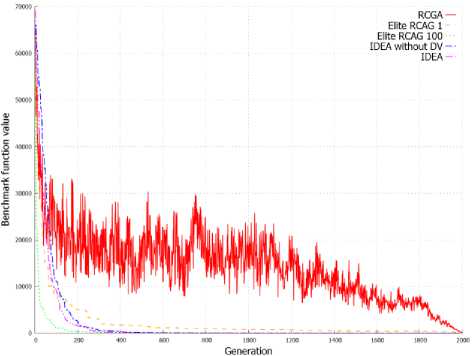
(a) f ₁

(d) f ₇

(e) f ₈

RCGA -

Elite RCAG 1

Elite RCAG 100 IDEA without DV —

(b) f ₂

(f) f ₉

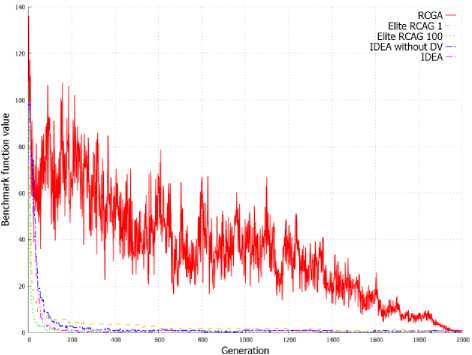
(c) f ₄

Fig. 2. Changes of the objective function value in successive generations for best individual.

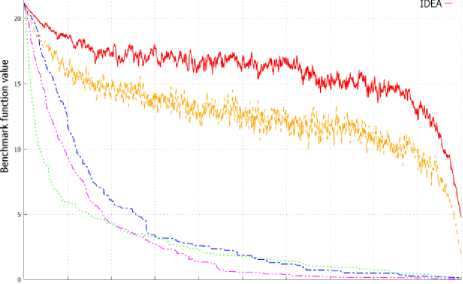
Figure 3. shows the average value of benchmark functions for solution represented by the population in the subsequent generations. Graphs from Figure 3 allow to observe a similar dependency as in case of evolution of best individuals presented on Graphs from Figure 2. IDEA allow to obtain a better best individual, but also obtain population with a higher average value of fitness function in successive generations. This can be observed on all graphs from Figure 3 and is clearly visible in Figure 3d and 3e.

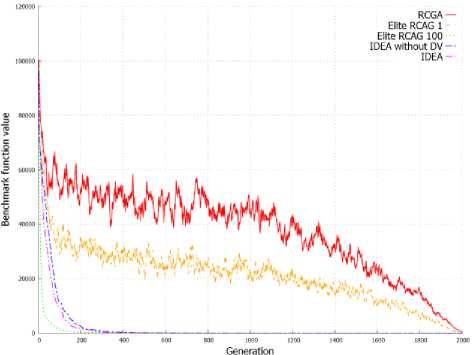
(a) f ₁

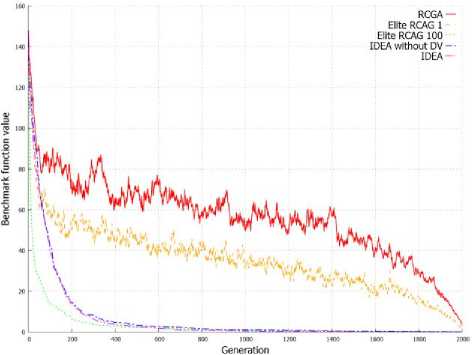
(b) f ₂

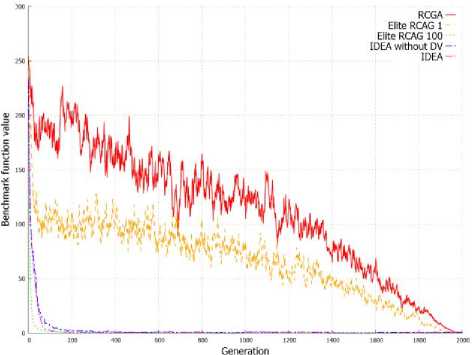
(c) f ₄

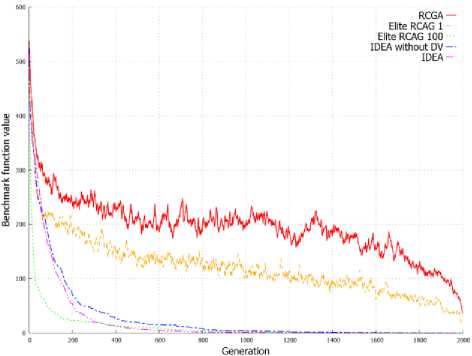
(d) f ₇

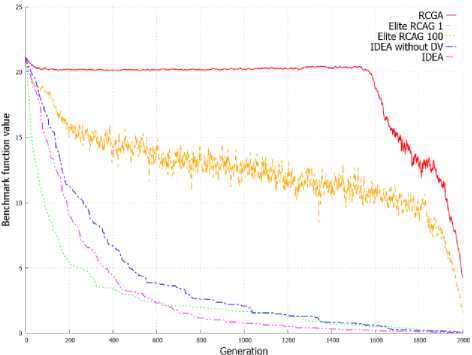
(e) f ₈

RCGA

Elite RCAG 1

Elite RCAG 100 IDEA without DV

0          200         400         600         BOO         IODO        1200        HOT        1603        1803        2030

Generation

(f) f ₉

Fig. 3. Changes of the objective function average value in successive generations for population.

V.Conclusion

This paper presents simulation analysis of developed evolutionary algorithm based on independent evolution of selected individuals. The achieved results of this study show, that the proposed algorithm IDEA provides better results than other popular EAs used in the study. The

DNUM operator allows to narrow the mutation scale in successive generations. Post-selection process allows to monitor and correct the direction of the independent evolution of individuals. The main idea of algorithm IDEA focuses on monitoring independent evolution of population individuals. Improving the average value of fitness function for population is only additional effect. The improvement of algorithm performance without increase number of calculation objective function value is useful for application of algorithm to solve real-life problems.