Индивидуальное прогнозирование двигательного развития у больных детским церебральным параличом на основе подходов статистического анализа

Актуальной проблемой математического моделирования является применение методов статистического анализа при исследовании медико-социальных систем.

Одна из важных задач междисциплинарного взаимодействия современной медицины, механико-математических методов и информационных технологий заключается в достоверном прогнозировании динамики состояния человека на основе данных начального этапа формирования болезни.

При разработке прогнозных моделей, наряду с определением общих закономерностей развития заболевания у выборочной группы пациентов, важным представляется учет индивидуальных характеристик конкретного больного для получения более точных индивидуальных прогнозов.

Методы многомерного статистического анализа широко применяются в различных областях медицины [2, 4, 6, 8, 12]. Вместе с тем одним из малоизученных направлений исследования является прогнозирование состояния больных с врожденными нарушениями двигательных функций, на текущее развитие которых во многом влияют родовые и дородовые факторы риска. К таким больным, в частности, относятся дети с церебральными параличами.

Ташкинов Анатолий Александрович, д.ф.-м.н., профессор, первый проректор, Пермь

Вильдеман Александр Валерьевич, младший научный сотрудник кафедры МКМК, Пермь

Целью настоящей работы является создание математических моделей прогнозирования двигательного развития у больных детским церебральным параличом (ДЦП) на основе подходов статистического анализа.

Анализ исходных данных

В качестве комплексного показателя двигательного развития рассматривается индекс моторики – величина, характеризующая интегральный уровень развития моторных навыков [13].

Объектом исследования является ребенок с детским церебральным параличом, в результате обследования которого определены значения множества факторов, характеризующих его состояние. В работе исследовалась выборка, состоящая из 157 наблюдений, соответствующих 73 больным. Данные были получены в результате совместной работы с Пермским Центром комплексной реабилитации инвалидов. Выборка формировалась в результате случайных обращений пациентов в медикосоциальное учреждение в течение 10 лет. При этом, несмотря на достаточно большое количество людей с диагнозом ДЦП, обследованных на протяжении данного промежутка времени, удалось выделить только 5 больных, регулярно наблюдаемых в течение всего рассматриваемого периода. В связи с этим исследуемые в настоящей работе модели прогнозирования будут иллюстрироваться на примере группы из пяти человек.

Во время обследования у каждого больного экспертным путем оценивались 12 различных групп двигательных навыков по пятибалльной шкале. В результате суммирования всех навыков определялось значение индекса моторики, лежащее в интервале от 0 до 60.

Изменение индекса моторики с возрастом у группы пациентов рассматривалось как случайный процесс Y ( t ) с непрерывным временем и непрерывными состояниями [3, 11], где t – возраст в месяцах. Динамика изменения индекса моторики у j больного в группе в этом случае является реализацией y ^{( j )} ( t ) случайного процесса Y ( t ) .

В силу случайности обращений пациента в лечебные учреждения y ^{( j )} ( t ) представляет собой неэквидистантный временной ряд, т.е. характеризуется случайными интервалами времени между отсчетами. Для регуляризации временного ряда в работе использовался метод скользящего среднего, основанный на представлении y ^{( j )} ( t ) в некоторой точке посредством взвешенного среднего значений, наблюдаемых в окрестности этой точки [1].

С целью исследования структуры случайного процесса была построена корреляционная функция oo

Ht M [ Y ( t ) Y ( t ')] r y ⁽ t , t) = D [ (D^

oo                   o где Y(t) и Y(t') - сечения центрированного случайного процесса Y(t) в моменты времени t и t', Dy (t) и Dy (t') - дисперсии Y(t) в моменты t и t'.

На рис. 1 приведена диаграмма рассеивания для пяти реализаций случайного процесса Y ( t ) , на рис. 2 изображен график соответствующей корреляционной функции при фиксированном t = 15 .

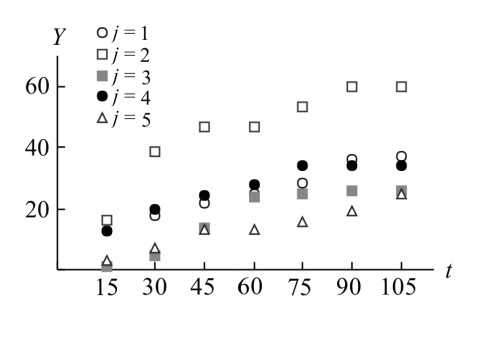
Рис. 1. Реализации индекса моторики на примере пяти больных

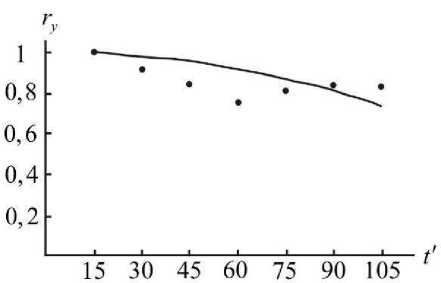
Рис. 2. Корреляционная функция индекса моторики

Анализ корреляционной функции данного процесса показал, что для него характерна достаточно сильная вероятностная зависимость между сечениями, что говорит о простой структуре процесса с плавно меняющимися реализациями.

Определение среднегрупповой зависимости индекса моторики от возраста

Для получения достоверных прогнозов относительно будущего состояния больного необходимо учитывать при построении прогнозных моделей индивидуальные характеристики конкретного пациента.

Вопросы индивидуального прогнозирования подробно рассматриваются в работах Ю.П. Самарина и его учеников [5, 9] применительно к прогнозированию состояния механических объектов.

Суть методов индивидуального прогнозирования заключается в переходе от уравнений, описывающих осредненное состояние группы пациентов, к уравнениям, характеризующим конкретного больного.

В соответствии с подходом индивидуального прогнозирования на первом этапе вычисляется средний индекс моторики для группы больных.

Для определения зависимости среднего индекса моторики от времени было проведено осреднение процесса Y ( t ) по реализациям. Задача аппроксимации полученных таким образом средних значений состояла в выделении тренда временного ряда f ( t ) .

При определении тренда использовался параметрический метод, основанный на предположении о наличии математической модели зависимости, заданной с точностью до параметров:

Q f (t, 0) = a 0 + £ aq ф q (t, X q ), (2)

q = 1

где 0 = ( a 0 a 1 ... a q ... a_Q X 1 ... X _q ... X Q ) - вектор неизвестных параметров, ф _q ( t,X_q ) -базисные функции, заданные с точностью до параметра X _q.

В настоящей работе для определения зависимости f ( t ) применялся метод последовательного выделения экспоненциальных слагаемых, предложенный впервые Ю.П. Самариным [10].

В соответствии с данным методом в качестве базисных используются функции вида

Ф q ⁽ t , ^X q ) = ¹ - e ^^ q .

Применение базисных функций (3) в настоящей задаче обосновано тем, что всякую непрерывную на конечном отрезке функцию можно с любой степенью точности приблизить степенным полиномом (теорема Вейерштрасса), а разложение (3) сводится к степенному полиному подстановкой t = - ln x .

К числу особенностей метода относится то, что необходимое количество оцениваемых параметров X q не задается заранее, а определяется в процессе расчета. Кроме того, предполагается, что данные параметры значительно отличаются друг от друга, это позволяет с достаточной степенью точности описывать отдельную дугу аппроксимирующей кривой с использованием только одного из параметров.

В результате применения метода нелинейная зависимость среднего индекса моторики от возраста была аппроксимирована с помощью двух экспоненциальных слагаемых (рис. 3, 4):

f ( t ) = - 16,49 + 66,87(1 - e ^- °^,°°⁴t ) + 28,39(1 - e — °,⁰⁹ t ).                    (4)

~    ~~

Коэффициент детерминированности   R ² = 1 - £ ( f i - f i ) ² / ^ ( f i - ( f i ))   для

i

i

аппроксимации (4) составил 0,99 .

При этом было получено, что параметр X ₂ = 0,09 в выражении (4) характеризует динамику индекса моторики на интервале t е [0; 45), а X 1 = 0,004 - на интервале t е [45; 105].

Отличительной чертой метода последовательного выделения экспоненциальных слагаемых является то, что он позволяет получить аппроксимирующее выражение, описывающее различные участки кривой индекса моторики с помощью различных параметров X q , не прибегая при этом к использованию кусочно-гладких функций.

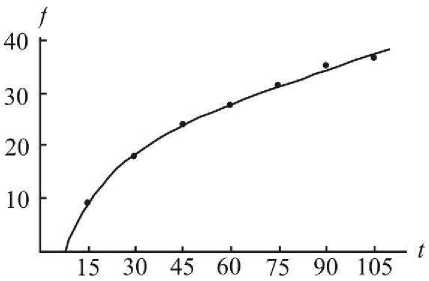
Рис. 3. Тренд среднего индекса моторики, полученный с использованием двух экспоненциальных слагаемых

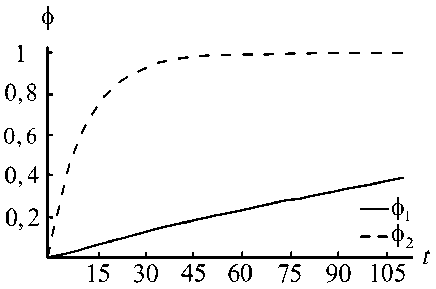
Рис. 4. Базисные функции, используемые при аппроксимации

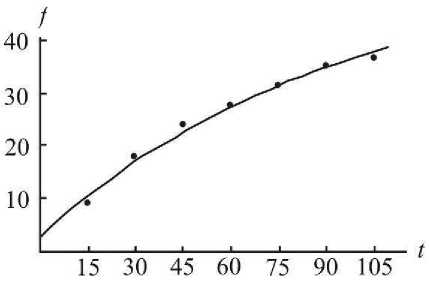
Рис. 5. Тренд среднего индекса моторики, полученный с использованием одного экспоненциального слагаемого

Для сравнения зависимость среднего индекса моторики от возраста может быть аппроксимирована с использованием одного экспоненциального слагаемого (рис. 5). Однако коэффициент детерминированности при этом будет меньше: R ² = 0,98.

Кроме того, сам характер кривой индекса моторики, полученной с помощью аппроксимации двумя экспоненциальными слагаемыми (см. рис. 3), более точно соответствует развитию моторных навыков на начальном этапе у больных ДЦП, для которых, как правило, характерна задержка начала двигательного развития.

Индивидуальное прогнозирование индекса моторики

При построении моделей индивидуального прогнозирования вместо среднего индекса моторики рассматривается случайная функция:

Q

Y ( t ) = A + £ A q ( t )(1 - e q t ),                               (5)

q = 1

где A q ⁽ t ) = A q ⁺ A ’ ⁽ t);

A q ( q = 0, Q ) - случайные величины, для которых AA_q^ = a q ;

A'’ ( t ) - центрированные случайные функции, для которых AA( ( t )^ = 0 ;

X _q ( q = 1, Q ) - детерминированные величины.

Таким образом, функция (5) представима в виде

Y (t) = F (t)+^( t),(6)

где

Q

F (t) = Ao + £ A, (1 - e Xq •'),(7)

q = 1

Q

^( t) = £ Aq (t )(1 - e ~X ■').(8)

q = 1

F ( t ) будем называть главной составляющей индекса моторики, ^ ( t ) будем рассматривать как наложенный «шум».

Считая, что значения шума существенно меньше главной части, будем искать индивидуальную зависимость индекса моторики от времени в виде аппроксимации (7).

Для j пациента выражение (7) примет вид

F (4 t ) = A ^j) + fX ^{j )} (1 - e q ), q = 1

где A qj ) ( q = 0, Q ; j = 1, N ) - реализации случайных величин A_q .

Выражение (9) содержит Q + 1 неизвестную A qj ) . X _q считаются известными, определенными при выделении группового тренда f ( t ) .

Задача индивидуального прогнозирования заключается в том, чтобы по ряду измерений состояния больного на начальном интервале протекания заболевания т ₀ спрогнозировать развитие его состояния в будущем.

Для подбора неизвестных A_q ^{( j )} воспользуемся методом наименьших квадратов на интервале т ₀. Исходя из анализа структуры Y ( t ), F ⁽ j ) ( t ) будем искать в виде монотонно возрастающей функции, что соответствует выполнению условий Af¹ >  0 ( q = L Q ).

В результате получаем следующую постановку задачи оптимизации с ограничениями типа неравенств:

<

1L ( F ^{( j} ) ( t, ) - y (^j ) ) 2 ^ min, i = 1

A(j) > 0 (q = 1Q), где n0 - количество измерений на интервале т0;

j = 1, N - условный номер больного, в настоящей работе рассматривалось N = 5 больных;

y i ⁽ j ) - измерения индекса моторики у j пациента в i момент времени; t i е т ₀.

Решение системы (10) может быть найдено численно, например одним из градиентных методов, либо аналитически по теореме Куна–Таккера [7].

В качестве примера продемонстрируем возможности метода индивидуального прогнозирования для больного ( j = 2 ), динамика двигательного развития которого наиболее сильно отличается от среднегрупповой (рис. 10).

Предположим, что в качестве исходных данных имеются три замера индекса моторики в течение первых четырех лет жизни пациента, а также тренд среднего индекса моторики, определенный ранее для группы больных (рис. 6). Задача состоит в прогнозировании индивидуального двигательного развития на ближайшие пять лет.

Как видно из рис. 6, индивидуальные замеры на начальном этапе развития заболевания очень плохо согласуются со средней зависимостью индекса моторики для группы больных. Поэтому прогнозирование на основе только группового тренда не приведет к получению результатов приемлемой точности.

С другой стороны, прогнозирование на основе только индивидуальных данных также не будет точным в связи с малым количеством замеров индекса моторики, а также в связи с тем, что период основания прогноза меньше периода, на который строится прогноз.

Для решения поставленной задачи целесообразно применить описанный ранее метод индивидуального прогнозирования, позволяющий скорректировать значения параметров групповой модели f ( t ) с использованием индивидуальных данных конкретного больного.

Решая систему (10) аналитически, используя теорему Куна–Таккера, находим реализации A q , доставляющие минимум в задаче оптимизации: A (²⁾ =- 64,17, A 1⁽²⁾ = 49,48, A 2²⁾ = 104,34.

На рис. 7 построена полученная таким образом индивидуальная зависимость. Коэффициент детерминированности для всей кривой составил при этом R ² = 0,96.

Как видно из рис. 8, модель индивидуального прогнозирования существенно точнее описывает контрольные данные (серые точки) по сравнению с групповым трендом.

Для оценки точности индивидуального прогноза был построен 95%-й доверительный интервал А = t _р S p (рис. 9), где S p - средняя квадратическая ошибка прогноза, t р - значение t -статистики Стьюдента для доверительной вероятности р .

Увеличение интервала основания прогноза т ₀ приводит к улучшению коэффициента детерминированности R ² , что говорит об адекватности построенной модели. Так, для т ₀ = 30 ( n ₀ = 2) - R ² = 0,76; для т ₀ = 45 ( n ₀ = 3) - R ² = 0,96; т ₀ = 105 ( n ₀ = 7)- R ² = 0,98.

Применяя изложенный метод к прогнозированию индекса моторики для оставшихся пациентов из группы, получаем индивидуальные кривые, изображенные на рис. 10. В таблице приведены соответствующие коэффициенты детерминированности.

F

60 -

40 "          •

20 " . ,^ ''

15 30 45 60 75 90 105 '

Рис. 6. Индивидуальные замеры (точки) и групповой тренд (пунктирная линия) индекса моторики

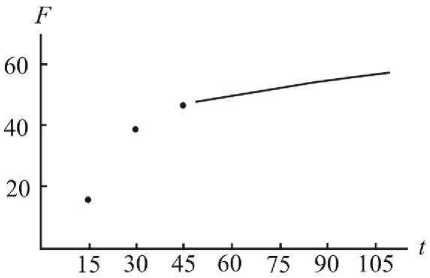
Рис. 7. Индивидуальные замеры (точки) и индивидуальный прогноз (сплошная линия) индекса моторики

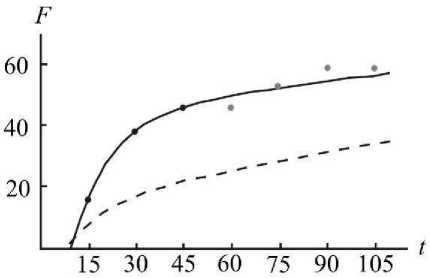
Рис. 8. Индивидуальные замеры (точки), индивидуальный прогноз (сплошная линия) и групповой тренд (пунктирная линия) индекса моторики

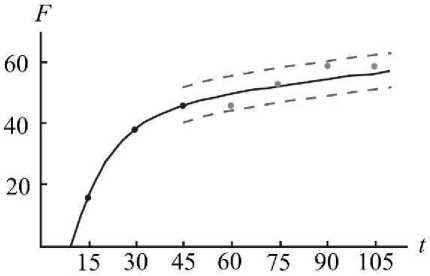
Рис. 9. Индивидуальные замеры (точки), индивидуальный прогноз (сплошная линия) индекса моторики и соответствующий ему 95%-й      доверительный интервал

(пунктирная линия)

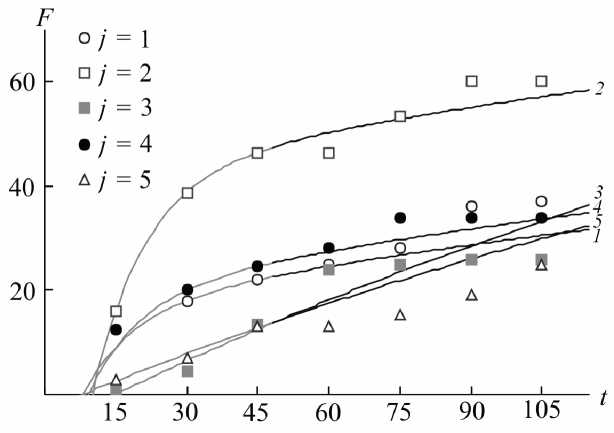
Рис. 10. Индивидуальные замеры и индивидуальные прогнозы индекса моторики

Коэффициенты детермини рованност и для кривых на рис. 10

Номер реализации j	1	2	3	4	5	Итого
R 2	0,84	0,96	0,85	0,95	0,60	0,84

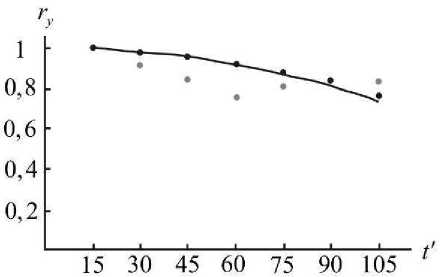
Рис. 11. Значения корреляционных функций, полученные для прогнозных (черные точки) и реальных (серые точки) данных, и кривая аппроксимации реальной корреляционной функции

С целью проверки достоверности построенных прогнозных моделей, в отсутствие независимой контрольной выборки больных, были получены значения нормированной корреляционной функции для модельных данных прогнозирования индекса моторики (рис. 11).

При этом значения модельной корреляционной функции практически точно легли на кривую, полученную в результате аппроксимации данных реальной корреляционной функции зависимостью вида 1 - α t ² , что свидетельствует об адекватном моделировании структуры случайного процесса.

Заключение

Предложенный метод индивидуального прогнозирования представляет собой эффективный инструмент обработки и анализа статистических данных, что было подтверждено применением данного метода при прогнозировании двигательного развития у больных детским церебральным параличом.

Полученные математические модели позволяют с достаточной степенью точности описывать динамику развития моторных навыков в условиях, когда интервал основания прогноза меньше периода, на который строится прогноз.

С целью дальнейшего улучшения достоверности индивидуальных прогнозов планируются исследования влияния, оказываемого на динамику индекса моторики со стороны родовых и дородовых факторов риска, определяющих начальные условия формирования двигательных навыков у больных детским церебральным параличом.

Применение предложенных методик прогнозирования в медицинской практике лечения детского церебрального паралича может служить дополнительным источником информации, характеризующей динамику состояния больного и используемой в процессе принятия решений специалистом в области реабилитации инвалидов.

Благодарности

Работа выполнена при финансовой поддержке РФФИ (грант № 10-04-96096-р_урал_а).