Inflationary models based on generalized exact cosmological solutions

Within the framework of constructing current cosmological models, the stage of cosmological inflation is important, since during this stage various physical processes occur that determine the further evolution of the universe [1, 5].

Various gravity theories are used to construct models of cosmological inflation, including Einstein gravity (GR) and the teleparallel equivalent of general relativity (TERG) [3, 4, 5].

Teleparallel gravity is a special case of metric-affine gravity, an important feature of which is the use of non-Riemannian geometry. Unlike Einstein gravity, teleparallel gravity does not have geodesic line equations. Force equations describe the motion of particles under the influence of gravity, and instead of metrics, dynamic tetrads are used. Just as the Levi-Civita connection which provides a way to naturally

Работа Фомина И.В. выполнена при поддержке гранта РНФ № 22–22–00248.

differentiate vector fields on a Riemann manifold, in teleparallel gravity the Weizenbock connection with torsion and zero curvature is used [5].

It can also be noted that to construct and analyze cosmological models, different methods are used including exact and approximate solutions of the cosmological dynamic equations [5]. A review of various methods for constructing exact cosmological solutions for the case of Einstein gravity is given in [5, 6]. We also note that all these methods can be used in constructing exact solutions of the equations of cosmological dynamics based on TEGR [7].

However, it should be noted that these methods make it possible to construct a limited number of exact solutions to the equations of cosmological dynamics in explicit form. Also, in the context of construction of the exact solutions of the cosmological dynamics equations in explicit form, as a rule, fairly simple types of evolution of scalar fields or types of cosmological dynamics are considered.

In this paper, we propose a method for constructing an unlimited number of exact solutions of cosmological dynamic equations with a complex form of the volution of a scalar field and a complex form of the cosmological dynamics based on the generating function of a special type for the case of GR and TERG.

It is also shown that in the case of a special choice of the constant parameters of the cosmological models obtained by the method, they correctly describe the dynamics of the expansion of the universe at different stages of its evolution.

• 1.    Cosmological models based on the teleparallel gravity

Teleparallel gravity is a well-known modification of Einstein gravity, in which tetrads e ® or components of the tetrad field е _а ( х ^ ) are used instead of a metric.

The tetrads form an orthogonal coordinate basis for which e ^ e ^ = * and e ^ e ^ = 第 .They relate the space-time metric д ^” and the Minkowski tangent space metric 77 ab = 成 ag( - 1,1,1,1) as follows [5, 8]

(1.1)

呢"= ^e p, ^e “ ⁷ ab .

Characteristic quantities of teleparallel gravity: torsion scalar T = S _p^ T %小 superpotential S _p^ and the distortion tensor К 望 ,which are specified in the components of the tetrad field [5, 8]

T% = e p (乙 e a - d ” e £ + 3 时 - 诚” e ^ ) ,                      (1.2)

S p“" = 2 ( к 华 + 端 T ” - % t 号) ,                       (1.3)

К н” = -^{1 (} 7 丛” 一 т ”н 一 T н” )

(1.4)

where 3 bH = 徴⑺勿八彳⑵ is the spin connection, A a (rc) is the local Lorentz transformations.

To construct and analyze models of cosmological inflation with a non-minimal connection between the scalar field and torsion, let us consider in the system of units 8ttG = c = 1 the following action [8]

S

/ d⁴xe [/(T, 0) + з(ф)Х ],

(1.5)

where /(T, ф) is some arbitrary function of the scalar field ф and torsion T , з(ф) is the kinetic function, Х = - 2 д н фд ^н ф is the kinetic energy of the scalar field and e = de 力 (e /) = ^/- ^ .

To describe inflation dynamics in the case of a spatially flat Friedman-Robertson-Walker (FRW) metric ds2 = -d力2 + a26ijdxld^^,                                    (1.6)

where q = q(" is the scale factor, the following tetrad is considered e/ = d沁g(1, q, q, q),

(1.7)

taking into account the Weizenbock connection

®%н = °-

(1.8)

In this case, the background dynamics equations corresponding to the action (1.5) are written as follows [8]

/(Т, 。 ) - з(0)Х - 27/ ① =0,                                    (1.9)

/(Т, 。 ) + ^ ( Ф ) Х - 2Т/ ,г - 4Л7r - 4Л7r = 0,                  (1.10)

—з,@Х — 3 ® (0)Н 。 一 з ( ф) 。 + / ,0 = 0 ,                             (1.11)

where Н = ^ is the Hubble parameter, Т = 6W ² is the torsion scalar and / ,r = 等 •

Also note that the canonical scalar fields correspond to the case ® > 0 , for phantom fields ® < 0 , based on the possibility of the following redefinition of the fields 夕 =/ J ®(ф) "ф .

The choice of the function / = /(Т, ф) determines the form of the theory of gravity in the cosmological models under consideration.

In works [9, 10], exact solutions of the system of equations (1.9)–(1.11) were obtained for an arbitrary Hubble parameter with a function /(Т, ф) = - G( 。 ) ， T - V(ф) , where G = G( 。 ) is the coupling function of the scalar field and torsion.

Now, we consider the special case

/ (Т, ф) = - Т - V (ф),

(1.12)

corresponding to the teleparallel equivalent of general theory of relativity (TEGR), where V = V (ф) is the potential of the scalar field, the equations of cosmological dynamics (1.9)—(1.11) for ® = 1 reduces to the case of cosmological inflation based on Einstein gravity

3Н ² = 2ф ² + V (ф), - 3Н ² - 2H = 2ф ²- V (ф), ф + 3Нф + & = 0,

(1.13)

(1.14)

(1.15)

where V 。 = 翡 and a dot represents a derivative with respect to the cosmic time 之

Also, we note that for the case of inflationary models based on general relativity one has the same dynamical equations [ ? ], for this reason, the methods for constructing generalized solutions of the system of equations (1.13)-(1.15) are the same for the cases of GR and TEGR.

2. Generalized exact solutions of cosmological dynamic equations

Since only two equations in system (1.13)-(1.15) are independent, they can be rewritten as follows

V ⑴ =3H ² + H, ф ² = - 2H.

(2.1)

(2.2)

In order to get exact solutions for the case of complex dynamics, let us consider a scalar field ф = ф« ) and a Hubble parameter H = H( 力 ) as follows

。⑴ = ± 4 ^ln [( Cb(Z ： F)2 ] 干 ABt + ^ф ₀ ,

(2.3)

H (t) = A ² In

n ( t)K/2 b B

( Cb ( t ) + F 严

2A ² Cb    A ² B ²

+ Ca ( t ) + F -。 ^t + 》

(2.4)

where functions ст = ст« ) and и = u ( t ) are related as follows

(2.5)

[—)+ К— = 0,с = const, \e/ u and А, В, С, Е, F, К, A, 0° are arbitrary parameters.

By direct substitution, one can verify that system (2.3)–(2.5) fully correspond to the cosmological dynamics equation (2.2).

The main feature of the proposed representation of the equations of cosmological dynamics is the specific choice of the generating function с = a(t) , which leads to the possibility of constructing an unlimited number of exact solutions.

As the example of prosed approach, we consider the function a(t) in the following form

c(t) = с о У

傍必

(t + m ) q

0 0 传          C o ? /  传^-1必

( q - 1)(t + m) ^ ^{- 1} * q - 1 丿 (t - m) ^ ^{- 1}

where с о = const and c(t) may be represented as the series

C(t ) = с" £ С ^ J^-m ) P       ,

⁰ 丿 (t + m) q       ⁰ 乙 P (q - к - 1)(t + m)i^{- 1} '

(2.6)

(2.7)

where C p = ^ ( Дф.

us to construct unlimited number of exact cosmological

The representation (2.7) of c(t) allow solutions in the explicit form.

By substituting (2.7) into (2.5), we get

/           2    / ( ? ² + q ²) t + 户 m 、

(2.8)

u(t) = uo(t + m) Km t Km exp ——ттгу——<—— , \ Kt(t + ?)丿 where uo is an arbitrary constant.

Thus, from (2.3)–(2.5) and (2.6)–(2.8) we obtain explicit exact expressions for the scalar field and the Hubble parameter

0(t)= АIn I ------------^---------^ I - ABt + 0o,

(2.9)

\ ^{(t + m )} q (^Сс 0 (/ (Jj ) q 必)^{+ F}) 丿

Я(t) = A ² In ((

^ 0 t ^p

（ 土 + m ） q

) в ( u ° (t + m) ^- KKm t Km exp (

( p ² + q ² ) t + p ² j Kt ( t + m )

))「 A 2 B 2 t

( ^Сс 0 (/ ( t + ^F ^rft ) ^{+ F} )

+ ^A,

(2.10)

or, in the other form

0(t) = A ln

Я (t) = A ² In

Е ( £ C / ( - m) ^{p -} 左 (t + m 尸^- q)

M=0                  丿

( - Ž 5 (J+X-) ) + ^F ) ：

- ABt + 0 0 ,

( C i R e,p ( t + j )) К" 信 C= ( - m)i (t + m) * ^-q[

( ^C ( - £ 5 (Л/—) ) + ^F 『

2A ² C ( £ C ^ ( - m) ^{p -} " (t + m) " ^{- q})

+ 仁 0

^C ( - 玄 C (i-⁽-j ； i) ) + ^F \  "=0                       /

A ² B ² t

+

+ ^A,

(2.11)

(2.12)

where a sum of a series itself and any summand are the exact solutions of equation (2.2).

Also, from (2.1) and solutions (2.13) we can reconstruct the type of the potential evolution in explicit form. However, due to the fact that the expression for the evolution of the potential is quite cumbersome, the form of function V = V ⑴ is shown in Fig. ?? for the certain values of the constant parameters of the inflationary model.

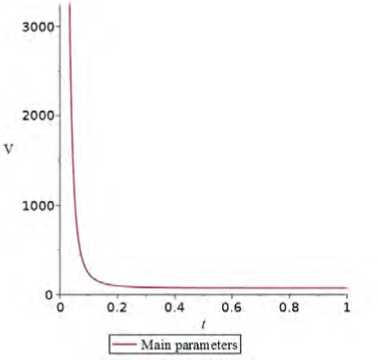
Рис. 1. The potential evolution V ( t ) for parameters p = 2 ,q = 3 , m = 1 ,A = 1 ,B = 0 . 01 , C = 1 ,K = 1 , ^ o = 1 , F = 1 , E = 11 , 0 o = 10 . 6 , A = 1 .

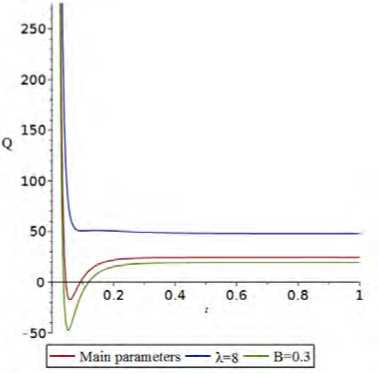
Рис. 2. The relative acceleration Q for parameters p = 2 ,q = 3 , m = 1 , A = 1 , В = 0 . 01 , C = 1 ,K = 1 , ^ o = 1 , F = 1 , E = 11 , 0 o = 10 . 6 , A = 1 .

We will also check the cosmological model basad on the solutions (2.11)–(2.13) with the selected parameters for exit from the inflationary stage and the presence of a stage of the second accelerated expansion of the universe.

For this purpose, we define the relative acceleration of the expansion of the universe as follows

Q = ^a = Я ² + H ,                                (2.13)

Q where Q > 0 corresponds to the accelerated expansion of the universe and Q < 0 corresponds to the decelerated expansion of the universe.

From Fig. ?? one can see that the obtained solutions for the selected parameters correspond to both the exit from inflation and the second accelerated expansion of the universe.

We also note that these properties of cosmological models based on solutions (2.11)–(2.13) can be obtained for other values of constant parameters.

Conclusion

In this paper, we proposed a new method for constructing an unlimited number of exact solutions to the equations of cosmological dynamics for the case of Einstein gravity and the teleparallel equivalent of general relativity.

The specificity of the method is the reduction of dynamic equations to a special form and the choice of a generating function ст = tr (。， which allows one to obtain an unlimited number of exact solutions.

Topical issues for further development of this approach are the construction of exact solutions with the scalar field potential in explicit form V = V(0) , the correspondence of the cosmological models obtained by these method to observational constraints on the values of the parameters of cosmological perturbations, and the analysis of approximate solutions following from physically motivated approximations.