Инфлатон и поле Хиггса в конформной теории супергравитации

Согласно принятой в настоящее время точки зрения темная энергия соответствует вакууму, который является однородной средой с постоянной положительной плотностью энергии. Уравнение состояния данной среды, связывающее ее давление и плотность, имеет вид р/р = —1 (1)

Это равенство довольно хорошо соответствует данным наблюдений. Среда, обладающая такими свойствами, может быть описана введением космологической постоянной (А-члена), как было предложено Э.Б. Глинером [1], [2].

Скалярные поля могут быть представлены в виде суммы классического вакуумного среднего и квантового поля, которое при вторичном квантовании превращается в оператор. Вакуумные значения скалярных полей соответствуют минимуму их потенциала. В точке минимума потенциал может быть отличен от нуля. Вакуумные средние скалярных полей естественным образом генерируют космологическую постоянную, и поля Хиггса, вообще говоря, не являются исключением, поэтому последние тоже должны быть включены в космологическую модель. Если бы темная энергия состояла из частиц, то в процессе космологической инфляции ее плотность не оставалась бы постоянной (или почти постоянной), а убывала бы по меньшей мере обратно пропорционально кубу масштабного фактора (если речь идет о тяжелых нерелятивистских частицах). Следовательно, данная среда вероятнее всего является вакуумом. С другой стороны, если бы вакуумные значения скалярных полей зависели от точки пространства времени, то массы элементарных частиц также зависели бы от пространственно-временных координат. Такое положение тоже не может считаться вполне удовлетворительным, поэтому среднее поля Хиггса считается постоянной величиной.

Известно, что на ранней стадии инфляции имело место сверхбыстрое расширение Вселенной. В изучаемой модели такое расширение не могло быть обеспечено полем Хиггса, так как поле Хиггса дает отрицательный вклад в энергию вакуума (это будет показано далее). Следовательно, для объяснения ранней инфляции необходимо введение дополнительного скалярного поля q называемого инфлатоном. Однако, на современной стадии инфляции вакуумное среднее инфла-тонного поля должно стремиться к нулю, так как, если бы это было не так, то оно давало бы вклад в массы элементарных частиц, а это противоречит экспериментальным данным, так как согласно стандартной модели массы частиц полностью определяются средним поля Хиггса. Таким образом, предполагается, что потенциал иііфлатоішого поля имеет минимум при q = 0. С другой стороны, согласно данным наблюдений в современную эпоху космологическая постоянная имеет положительное значение, поэтому в точке минимума при q = 0 потенциал должен быть положителен. Точное значение минимума потенциала должно соответствовать постоянной Хаббла, значение которой известно из наблюдений.

Интересно рассматривать возможности построения подобных космологических моделей именно в рамках теории супергравитации. Теория суперструн остается наиболее успешной теорией, позволяющей квантовать гравитцию. Низкоэнергетическим пределом теорий суперструн являются теории супергравитации. Поэтому разумно было бы для начала сформулировать четырехмерную теорию супергравитации, успешно описывающую инфляцию и согласующуюся с данными стандартной модели, а затем уже начинать поиски таких вариантов компактификации, которые позволяют вложить полученную модель в какую-либо из теорий суперструн. Другим преимуществом является тот факт, что в суперсимметричных теориях естественным образом появляются подходящие кандидаты на роль частиц темной материи, так как в результате нарушения суперсимметрии возникают стабильные массивные частицы.

Проблемой является то обстоятельство, что существует слишком широкий круг таких теорий супергравитации, поэтому целесообразно ввести какие-либо разумные физические принципы, ограничивающие спектр возможных космологических моделей. Одним из таких ограничительных принципов может служить конформная инвариантность. Существуют некоторые указания на то, что такая симметрия действительно может существовать в природе, на что указывет плато Харрисона-Зельдовича (см., например, [3]), возможное существоввание которого является следствием гипотезы о масштабной инариантности сверхранней Вселенной.

В любой суперсимметричной теории минимальное количество полей Хиггса, необходимое для успешной реализации механизма спонтанного нарушения электрослабой симметрии, равно пяти. Дело в том, что суперпотенциал не может содержать комплексно сопряженные поля, поэтому необходимо ввести не один изодублет полей Хиггса, а два таких изодублета, чтобы построить простейший калибровочный инвариант. В состав двух комплексных изодублетов входят восемь действительных полей. Три из них являются безмассовыми годлстоуновскими бозонами, соответствующими трем нарушенным генераторам симметрии. Эти безмассовые поля устраняются из лагранжиана за счет механизма Хиггса, и следовательно, остается пять физических скалярных полей Хиггса. Причем только один из них соответствует обнаруженному с помощью БАК нейтральному бозону Хиггса (а именно легчайший из них), а остальные четыре должны быть достаточно массивны, чтобы не вступать в противоречие с экспериментом. Одной из задач данной работы является проверка того, выполняется ли данное условие в предлагаемой модели.

1.    Модель

Конформно инвариантное действие N = 1 супергравитации было построено, например, в [4] с помощью метода, описанного в работах [5] и [6]. Такое действие в наиболее общем виде может быть представлено следующим образом

S = / "%( - ** ЕК(Ф*,е ^{- 2} % Ф)] 。 + [/(Ф)Е³]ғ + 2 Re\W_aC 。。 W^ ]ғ ) ,

⑴

为 = fgHV 。,                           (2)

a где Ф — мультиплет полей Ф> Ф2….Ф— реа，ғізутоЕ,ііх представление проігзволыюп уиитариоп калибровочной группы G, алгебра Ли которой определяется генераторами Та (эрмитовыми матрицами размерности N х N), Va — векторное калибровочное суперполе, обеспечивающее локальную инвариантность относительно преобразований группы G, К — кэлеров потенциал, W^ — напряженность суперполя V = TaVa, Е — левокиралыюе суперполе с конформным весом 1 (компенсатор), обеспечивающее конформную инвариантность действия (все остальные поля имеют нулевой конформный вес). В компонентных полях данное действие запишется следующим образом

S = / "%е[к(0*,0)О“/*О“/ + (^D^^*)K^jD^ф_j

(B*D"B)D“Kj +冋 2k『D"沙 D"亂(3)

+ 6 固 2K (ф*,ф)К-VF - V。- ((Б1 篇)2], где калибровочный производные имеют стандартный вид

D%・=д"фз-旳аВ^СТа犷办,⑷ i ...

D"/ = д“/ - у/,(5)

а также вводятся следующие обозначения к с   "2К   к дК Н дК

/= d^Ж ，/=/， ^k =麻，° =⁽内) .            ⑹

Поле /3 — компонента низшей размериости суперполя Е, а °с — соответствующие компоненты суперполей Фс, В^а — компонента низшей размериоти суперполя V ^а, А_м — калибровочное поле, соответствующее киральному генератору суперконформной группы (см. [7]). Потенциалы, определяющиеся Ғ и D- членами, имеют вид соответственно

V f = | 3 | 4КТ      (尸力)- 9 | / | 2 + 2 /| / | ² °^с°с + 6Ае(/ *.『 °с )),                ⑺

^С —包        入 *

⑻

⑼

/ П人，丿C     （丿丿, дФі

Vb = ] DaDa,  Da = %|例 ² К ( Та )『 Фс ・

Видно, что кинетические члены скалярных полей имеют неканонический вид, соответствующий нелинейной сигм а-модели. Их необходимо привести к каноническому виду. Для этой цели введем обозначение

3 =川 a

.

Учтем, что поле Ад не является динамическим, так как не имеет кинетического члена. Следовательно, его уравнение движения является алгебраическим уравнением. Поэтому это поле можно исключить из лагранжиана, выразив его через другие поля с помощью уравнений движения и подставив обратно в лагранжиан:

^д = 2^dн& + г (—J (^фС%^фс - ^фс^дд^фі

(П)

-2 旳 аВ 評 ( Та )『 Фс ) .

В результате этой подстановки поле a также автоматически исключается из действия, так как это единственное поле, входящее в лагранжиан, которое изменяется под действием киральных преобразований. Помимо полей Хиггса останется только дилатопное действительное поле о. Перейдем к модифицированному кэлеровому потенциалу с помощью стандартной формулы

^К (^ф*,^ф) = ехр^- * )•                                 ( 12)

Чтобы кинетические члены скалярных полей приняли в итоге каноническую форму, модифицированный кэлеров потенциал должен иметь следующий вид:

& ( ф*,ф ) = ф^сфс.

Дилатон о также исклточается из лагранжиана с помошьто вейлевских масштабных преобра ： зова-ний. Известно, что в результате преобразований метрического тензора,

Од” = 0 gд",

скалярная кривизна преобразуется следующим образом:

丘 =0 ^-1 , - 3 ▽产 ln0 - 3 д_д 1п0д ^д 1nq .

Наше действие содержит неминимальную связь скалярных полей с гравитацией, поэтому гравитационная постоянная является функцией скалярных полей и следовательно зависит от точки пространства-времени. Эту зависимость необходимо устранить и перейти от действия Йордана к действию Эйнштейна. Это можно сделать с помощью преобразования

.—呂 2 |/ 3 | ² К

g*" —    3   g*", и в результате перейти к правильному действию Эйнштейна-Гильберта, используя формулу

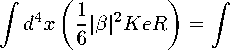
d4x

』巨丘-备 2% ln(|/3 | ² K)d* ln(|/3 | ² K )].

Сделав это, убедимся, что кинетические члены скалярных полей приобретают канонический вид:

s = /d⁴,e [- ； O*0 切 “2 + Ja - у - ：(与 " ) 2 ] .                 (18)

Мы видим, что дилатопное поле о исчезло из действия. Потенциал, уже не зависящий от дилатона,

имеет вид

У = ,4|^К2 卜 + 吃 ].                           ( 19 )

Для реализации механизма Хиггса вводятся два суперполя, являющиеся изодублетами SU (2):

为 =Й) ， % =(н+).                     ^{( 20 )}

Калибровочная группа имеет вид G = U (1) X SU(2).                                    (21)

Генераторы и константы связи запишем в виде а = 0,1,2, 3, То = \ (“2,Тз)=? = J,

2                                2                                  ( go = g‘, gi = g2 = дз = g.

где 戸一 матріш.ы Па у пи (матріш.ы 2 X 2). деііствутоттпіе на двумерные мультиплеты (20 》 У — гппер-заряд. Тогда калибровочное суперполе приобретает вид

坊 =У g’y+2 gJy.                           из)

Ковариантная производная примет вид

o*%,d = (d* Tg‘49 - igB*2)%心

Для того, чтобы в результате спонтанного нарушения суперсимметрии остался ненарушенным генератор электромагнитных взаимодействий

Q = Тз + У,(23)

гиперзаряды необходимо положить равными

К = 1, М = -1.(26)

Суперпотенциал и модифицированный потенциал Кэлера имеют вид

/ = 〃Hj еЯи + А + 巾 + рф2,(2-)

′′ d = Ф*Ф + 用е— v-gTVHn + 篤〃 V-gTVHd.(28)

По формуле (7) вычисляем потенциал

Vf = \^\4K-1\V_h + %],

где введены следующие обозначения

6 .

Vh = 后\〃\ ²( 雑% + 觴%)- 9\N² + 3 \"\ ² 隔 e% \ ²

-6Re(X*^H^eHu) + |k² [\* ² + \〃\ ² \我 1e 我 " \ ²                    (30)

+2Ae(* 〃〃 3eHu)] (HUHu + H^H_d),

% = J2 MF + 3/(HlHu + H ： Hd) [Re (*佯) + Re( 〃 H 彳 €%〃 *)]

— 12Re(* 〃 9 ) +—^Re( 〃 *pg) + 。 ( 屮 ²).

К2

Также к действию необходимо добавить суперперенормируемый член, обеспечивающий мягкое нарушение суперсимметрии (см. [8]):

^Vm = -1^^HU^Hu +  2^^H ： ^Hd ― ^Re(8 〃 ^H?^eHu).

2. Космологическое решение

Для простоты здесь и далее будем полагать, что все параметры вещественны. Для того, чтобы потенциал имел устойчивое положение равновесия (локальный минимум) при g = 0 необходимо, чтобы константы связи удовлетворяли соотношению, которое следует из равенства нулю первой производной от потенциала:

〃伙 К²f² ( 人 + "²) — 12 人 + ^^ ) = 0.                           (1)

Это условие экстремума. Константы всегда можно подобрать так, чтобы вторая производная была больше нуля, что соответствует условию минимума. Если 〃 = 0, то очевидно, что

К4

p = аК ²   -( A^² + 〃行 4) .                                     (2)

Для того, чтобы генератор электромагнитных взаимодействий оставался ненарушенным, вакуумные значения полей Хиггса должны иметь вид

О ， Hu = И

⑶

В этом случае массы W и Z бозонов примут вид

2 — g²S2 +。 ²⁾     2 — ( g² + g ' ² )( uU + 谓)

w =    2    , ^mz =       2

⑷

Для того, чтобы модель не противоречила экспериментальным данным, средние полей Хиггса должны совпадать:

^u = 3 d = 3.

⑸

В этом случае система вакуумных уравнений совместна, если mu и md совпадают. Введем обозначение

m2 = m2 = 三 u d

.

⑹

Подставляя (3) в уравнения Эйнштейна, можно получить решение, соответствующее космологической постоянной (темной энергии):

9 K2V2 「

Я2Пл = 9^ [2/ // + 4 〃 ² 。 ²/* - ЗА ² - 2 〃刈 ²

+ 〃 ² и ⁴ + М/( А ² + 〃 ² и ⁴ + 2 〃 Аи ²)]

⑺

+ 1m²K²v² -丄 8“² V², 6           3

где % — 'зііачеіше постоянной Хаббла в пастояший момент времени. Ол — от ноше пне плотности темной энергии к критической плотности энергии (также на текущий момент времени). Значения этих величин известны из данных наблюдений и на текущий момент составляют

Яо = (1.184 土 0.014) * 10^{- 61} /^{- 1} ,     Ол = 0.75 土 0.1.

⑻

Для того, чтобы определить минимум потенциала, необходимо потребовать равенства нулю первых производных по полям Хиггса от потенциала. Вычислив эти производные, можно показать, что вакуумные уравнения для полей Хиггса при условии (5) сводятся к одному уравнению

8 〃 = m~ + к' 4 ( 2 〃 ² + 6 〃 ² V ² — 2 呂 ² А ² + 2 呂 ² 〃 Av ² + 4 呂 ² 〃 ² v ⁴ +/ A ² v ² + 呂 ⁴ 〃 ² v ⁶ + 2k ⁴ A^v ⁴ + 4 〃 ² /呂 ² — 2А 〃 ) .

Отсюда легко выразить одну из констант связи:

/ = / [ я2Ол* + 9е “ 2 。 ² (5 〃 ² v ⁴ + ЗА ² — 3*A ² v ²

+3/ 〃 ² v ⁶ + v⁴/A ² + v⁸/ 〃 ²                   (10)

+2v ⁶ 呂 4А 〃 ) ] / (18е " 2 「 [1 —呂 ² V ² ]) .

Из этого равенства очевидно, что так как 呂 ²v² 《 1, то при 〃 = 0 нельзя получить положительную космологическую постоянную. Это говорит о том, что для описания темной энергии необходимо включение инфлатонного поля.

Теперь приступим к вычислению масс. Массы нейтральных бозонов Хиггса можно вычислить, подставив в потенциал выражения

%=(「) , 乜 = (二) .                 (И)

0              V +02/

Массовые матрицы реальной и мнимой частей 01 и 02 расщепляются, поэтому рассмотрим их по отдельности. Эти матрицы не диагональны. Чтобы вычислить массы, необходимо диагонализовать матрицы и перейти к реальным физических полям. Эти матрицы можно диагонализовать с помощью ортогональных преобразований. Тогда на диагонали будут стоять квадраты масс физических частиц. Диагональные элементы можно вычислить, решив характеристические уравнения.

Поля можно представить следующим образом:

01 =。 1 + 姉 1 ,   02 =。 2 + 乃 2 .

Тогда компоненты массовой матрицы определяются равенствами

2(MRe@),j

d ² V daidaj

2 （ m/m0 ）方

d ² V dbidbj

Массовая матрица реальной части симметрична и удовлетворяет равенству

(МНеф)11 = (Mr：.(15)

Компоненты определяются равенствами

5%2   m2   54е^2^2 , 2    222 - 2,22

^(MRe0 ) 11 = ^"2..1 2 1..^ 4 (4 + 4 片 0 +2n/ 片 — 其人

+742。2 + 8其242。4 + 其 64人06 + 4^4^206

+ 1 , ⁶V u ⁴ + 1 /〃 2 0 8 +4/ 人〃 0 ⁴ ) ,

,       .       27е^к 2 炉,

(MRe0 ) i2 =...4— (2 人川其 ² 0 2 + 2 〃 2 其 ² 0 ² + 2 片 ⁶ 4 人 0 ⁶ + T 6 A 2 0 ⁴

+左64208 + 124202 — 24人 + 16 其24204(i7)

- A 2 0 2 K ⁴ + 7 呂 ⁴ 4 ² 0 ⁶ + 6 其 ⁴ 人" ⁴ )

— B_M — .9 2 0 2 /2,

.92 = .2 + d2.(18)

Поэтому характеристическое уравнение det^MReф — mRe") = 0

(где / — единичная матріш.а) приобретает вид

((Мйе0)11 — mRej2 = (MRe°)22・

Масса легчайшего из нейтральных бозонов вычисляется по формуле

m* = (MRe0)11 + (MRe0)12

и имеет вид

m * = 54е “ ² 。 ² 卜〃 ² 0 ⁶ + 14 〃 ² 0 ⁴/М + М 〃 ² 0 ⁸ + _К ² А ² 0 ⁴

• - А ² 0 ² + 10 〃 ² 0 ² /呂 ⁴ + 6 人〃 0 ⁴ + 2 呂 ² 》〃 0 ⁶ )

+6(К202Я2Пл + 9产2 辰206 - 3/04А2

+3 呂 ² 0 ⁸ 〃 ² + 呂 4 0 ⁶ А ² + 呂 ⁴ 0 ¹⁰ 4 2 + 2 呂 ⁴ 0 ⁸ А 〃

+3А ² 0 ² ]) /(1 —* 0 ² ).

Предполагается, что это и есть бозон Хиггса, обнаруженный с помощью БАК. Масса второго нейтрального бозона определяется следующим образом:

m l = (MRe0 ) ll — (MRe0 ) l2 ,

m 2 = m ² + m ^ + 54г 2 : 2 ®² 0 ⁶ + 24 2 0 ⁴ /片 ² + А 2 0 ²

• — 2А ² /^ ² + 4 〃 ² /呂 ⁶ + 4 〃 ² 0 ² /呂 ⁴ + 2A 〃 0 ⁴ ) +6 [ я 2 П л + 9е " ² 。 ² (3А 2 /М + 5 〃 ² 0 ⁴ /М +3 〃 ² 0 ⁶ + *0 ⁴ А ² + *0 ⁸ 〃 ² +2*0 ⁶ А 〃 — 3А ² 0 ² ) ] /(1 — к ² 0 ² ).

Массовая матрица мнимых частей тоже симметрична. Ее компоненты определяются равенствами

(М/_тф ) іі

卅    54е^2^2 2 С 2 / 2    2\2

+       (/ + 2 / ² /川- /A²

+3 / ² 。 ² + 2 /〃 ²U⁴ + ； /A²/

+ ；呂 ⁴ 〃 ²u⁶ + 呂 ⁴A 〃 u⁴),

(Mim@)i2

54^ 2 炉八      2 、   2 、   「

...- ： — (A/z — 左 入№ )+8n.

K4

Легко проверить, что с учетом (9) эта

матрица удовлетворяет равенствам

(М1тф)11 = (МІтф)22 = (МІтф)і2.(27)

Поэтому масса одного из четырех нейтральных бозонов равна нулю:

欣=(Мітф)іі - (Мі^)і2 = 0.(28)

Это голдстоуновский бозон, который устраняется с помощью механизма Хиггса, объединяясь с векторной степенью свободы, а именно с нейтральным Z бозоном. Масса же последнего нейтрального бозона Хиггса отлична от нуля и имеет вид m2 = (Мі.)іі + (Мі^)і2,(29)

欣 =m 2 + 54І " 2 ®² 。 ⁶ + 2A “4 + a ² 。 ²

+4 〃 ² з ⁴ /т ² - 2A 2// + 4 / 2 /呂 ⁶ + 6/ ² ^ ² /к ⁴ )

+6 [н120A + 9е^2"2 (3A2/呂2 + 5/2。4/呂2

+3/² 。 ⁶ + ^²^⁴A² + ^²^⁸_M²

+2^ 2 ^⁶A_M - 3A²^²) ] /(1 - ^ 2 ^ 2 ).

Таким образом мы имеем три нейтральных бозона. Заряженные бозоны можно вычислить, подставив в потенциал выражения о，…

Реальные и мнимые части полей тоже не смешиваются, поэтому их можно рассматривать отдельно.

Массовые матрицы удовлетворяют равенствам

(Мд_е^) іі = (Мд_е^ ) 22 = (М1_m ，屮 ) ii = (М1_m ，屮 ) 22 = (Мд_е^ ) 12 = - (Мі_т^) і2 .

Решая характеристические уравнения, можно увидеть, что два из заряженных полей Хиггса имеют нулевые массы:

М2 = (М_Яе^ ) 11 - (М кз ) 12 = (Мі_т^)_п + (Мі_т^) і2 = 0.                (33)

Они также являются голдстоуновскими бозонами и устраняются из действия посредством механизма Хиггса, объединяясь с векторными степенями свободы, соответствующими заряженным 爪+ ii 爪- бозонам стандартной модели. Массы других двух совпадают 口 опредетятотся равенством m^ = (Мкз)и + (Мйе^)і2 = (Міт^)и - (Міт^)і2.

Точное выражение имеет вид m^ = m2 + 1 "患 + 54eК%2(Vo2 + 〃2o6 + 442// +4〃2u2// + 2〃2 v4/k2 -人2/片2 + 2人〃u4) +6m2Qa + 9еК%2 机2,// + 3A2/k2 -ЗА2 и2 + 3〃2u6 + /и4》2 + 川胪〃2

+2 呂 ² 。 ⁶

其 ² 。 ²)

Квадрат вакуумного среднего поля Хиггса равен

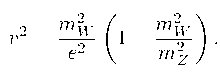
/ = mk ej

В планковских единицах это составляет примерно и2 心 1.334 • 10-33.

Нижняя граница масс бозонов Хиггса достигается при m = 0 и А = 0. В этом случае массы трех из них почти совпадают и удовлетворяют примерным соотношениям me 仁 mi 仁 m2 仁 3.455 • 1015m%.

Заключение

Таким образом, была построена суперсимметричная конформно инвариантная космологическая модель, описывающая современную стадию инфляции в соответствии с законом Хаббла. Модель предсказывает существование четырех дополнительных массивных частиц - двух нейтральных и двух заряженных скалярных бозонов. В работе были найдены массы этих частиц, а также получена зависимость постоянной Хаббла от констант взаимодействия и других параметров модели. Следует отметить, что в работе исследуется только современная стадия инфляции, когда инфлатонное поле близко к нулю, поэтому имеет смысл ограничиться разложением суперпотенциала по инфлатонному полю только до второго порядка малости.