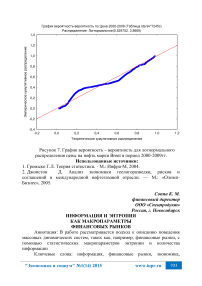
Информация и энтропия как макропараметры финансовых рынков

Любые экономические системы, в том числе и финансовые рынки, имеют такую особенность, как массовость, затрудняющую их непосредственное регулирование. Анализ и прогнозирование поведения каждого участника в отдельности нереальная задача. При этом, зачастую персональные цели участников не совпадают с потребностями общества, являющегося владельцем этой системы. Поэтому регулирование экономических систем осуществляется с помощью нескольких ключевых параметров (например, норма обязательных резервов), а анализ динамики состояния системы осуществляется с помощью макропараметров (например, различные фондовые индексы). На сегодняшний момент основными используемыми макропараметрами являются финансово-экономические (базирующиеся на ценах, натуральных объемах и их процентных соотношениях). Но в конце 1990-х годов появились идеи использования статистических макропараметров, в частности энтропии [1, 2, 3]. Данное направление науки получило название эконофизики, потому что ее идеи пришли из термодинамики, которая описывает макроповедение сред, состоящих из огромного количества частиц (атомов и молекул), индивидуальное поведение которых так же не может быть подвержено непосредственному управлению.

Основанием для переноса термодинамических законов являются следующие аналогии: очень большое количество участников, обладающих некоторой свободой поведения; парные взаимодействия; законы сохранения при взаимодействиях [4]. В таблице 1 приведена расшифровка соответствия аналогичных понятий.

Таблица 1

Соответствие понятий в экономике и термодинамике

Термодинамика	Финансовый рынок
Газ содержит большое количество хаотично движущихся молекул	Рынок содержит большое количество участников, которые постоянно изменяют свое состояние
Молекулы в газе постоянно взаимодействуют, соударяясь друг с другом в процессе хаотического движения	Участники на рынке постоянно совершают между собой сделки
При  соударениях  выполняется  закон сохранения энергии	В  любой  сделке  сохраняется  общее количество денег участников

1. ЗАКОН НЕУБЫВАНИЯ ЭНТРОПИИ

Одним из основных принципов термодинамики является второй закон [5], который гласит, что любые процессы в замкнутой термодинамической системе протекают только в направлении возрастания энтропии. С учетом трактовки энтропии, как меры беспорядка (хаоса) этот закон получил следующую нестрогую бытовую формулировку:  всякая массовая динамическая система без влияния извне стремится к максимально беспорядочному состоянию [6]. Приведем пример. Капнем в чашку кофе каплю молока. Если подождать некоторое время, то частицы молока равномерно распределятся по всей чашке, и уже никогда не соберутся обратно в каплю.

Для финансовых рынков имеют место аналогичные тенденции. Представим, что на некотором рынке с большим числом участников, скажем 50 тысяч человек, в начальный момент времени каждый участник обладает одинаковой суммой денег. Очевидно, что после совершения некоторого количества сделок состояния участников хаотически изменятся, и практически невероятно, что в некоторый момент времени в последующем исходная ситуация повторится (у каждого из 50 тысяч участников будет равная сумма денег).

В результате математического анализа упрощенных моделей (аналогов модели идеального газа в термодинамике) различных экономических систем [2, 4, 7] и, в том числе, финансовых рынков было строго доказано, что устойчивым положением равновесия для этих моделей является состояние с максимально возможным значением энтропии. Энтропия системы определяется формулой [7] от                                     от

$ = £ n(m)ln      = Л £ v(m)ln               1)

т=0           ^{v J}       т=0           ^{4  7}

Здесь п(т) - количество участников, обладающих состоянием т, N -общее количество участников системы, v(m) = п(т)/^ - доля участников с состоянием т. На рис. 1 представлена зависимость энтропии от числа проведенных сделок для модели простейшей экономики [7].

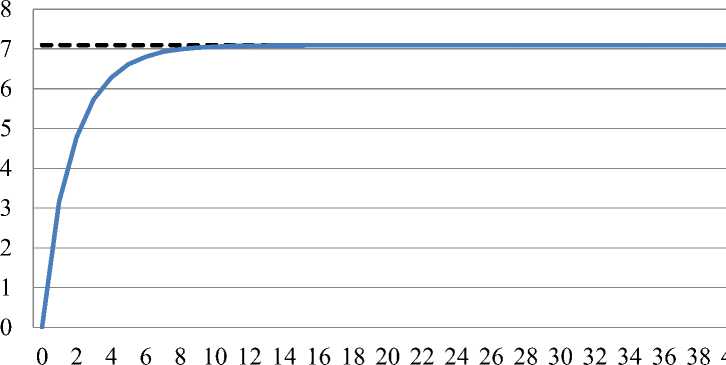
Рис. 1. Динамика изменения энтропии для модели простейшей экономики (N = 50000 участников)

Из рисунка видно, что в ходе эволюции (по горизонтали отложено количество проведенных сделок в десятках тысяч) энтропия системы растет пока не достигнет своего максимума (отмечено пунктиром). Это состояние системы является равновесным. Распределение денег между участниками в положении равновесия подчиняется экспоненциальному закону [7]

N   / m\

n(m) = -exp (-y), M()

–

где I =   0 /Щ - «среднее» состояние участников системы, а М₀

общее количество «реальных» денег в системе (аналог денежного агрегата М₀). Аналогичное распределение по уровням энергии имеют молекулы идеального газа [5]. Это распределение называется распределением Больцмана. В нем, в знаменателе показателя экспоненты стоит температура газа, поэтому в некоторых работах по эконофизике «среднее» состояние участников Т также называется температурой системы.

Открытой статистики по распределению денег у участников реальных финансовых рынков нет. Для проверки уравнения (2) были проанализированы доходы и состояния граждан США и Великобритании на основании подоходного и имущественных налогов (для указанных стран эти данные являются вполне репрезентативными) [8]. Также, была проведена оценка распределения доходов в США, Великобритании и России по распределению репрезентативных расходов, таких как покупка новых автомобилей [9]. Проведенный анализ подтвердил, что фактические доходы и состояния населения распределены в соответствии с экспоненциальным законом (2). Небольшое отклонение от экспоненты наблюдается только у 5% «самых богатых» состояний, которые распределены в соответствии с законом Парето п(т) = Ст ~^а .

• 2. ОЦЕНКА ВЛИЯНИЯ ИНФОРМАЦИИ НА ДИНАМИКУ ФИНАНСОВЫХ РЫНКОВ

Главной перспективой использования энтропии (1) для прогнозирования динамики финансовых рынков является ее трактовка как информационной емкости. Клод Шеннон доказал [10], что если мы получим N сообщений х из некоторого множества X, то, при N ^ т, суммарная информационная емкость последовательности этих сообщений будет близка к энтропии

S ~J⁽x 1 x₂ ...х^х^.

Примечание: в оригинале Шеннон доказал эту теорему для удельной энтропии на сообщение h = S/^ = limN^mJ/. Для количества информации используется логарифмическая мера J(x) = —lnp(x) [11] (здесь р(х) -вероятность сообщения х). Основанием для этого является тот факт, что для оптимального кодирования элемента из множества, содержащего К равновероятных элементов, необходимое количество кодовых символов пропорционально ln К.

Основным отличием финансовых рынков от термодинамических сред является подверженность участников информационному влиянию. Один из самых наглядных примеров – обвал 24 июля 2008г. котировок компании «Мечел» в результате распространения в СМИ фразы про доктора [12].

В термодинамике мы можем уменьшить энтропию, лишь затратив энергию «извне», например, сжав газ при постоянной температуре, совершив при этом работу А [5]. Поскольку финансовые рынки могут принимать более упорядоченное состояние (с точки зрения энтропии) под воздействием лишь только внешней информации мы вынуждены добавить еще одно «информационное» слагаемое в уравнение для изменения энтропии

as = ^au + ^a+j.

ТТ            3)

Примечание: первое слагаемое – изменение внутренней энергии – при постоянной температуре будет равно нулю. В термодинамике принято соглашение, что если А > 0, то это работа расширения газа, если А < 0, то это работа по сжатию газа, то есть при сжатии AS < 0. Для финансовых рынков первое слагаемое можно понимать как изменение суммарных активов рассматриваемой системы, второе слагаемое как некое «внешнее» принудительное (регулирующее) воздействие.

Предположим, есть некий инвестор, который располагает суммой М, и рассматривает разные варианты вложений своих средств. Его цель – максимизировать свой доход Xximi , где Xj - доходность i -го инструмента, а mi - сумма вложенных в этот инструмент денег. Если бы инвесторы вели себя как физические частицы, то они вкладывали бы весь свой капитал в инструменты с максимальной ставкой X j (в пирамиды). Тем не менее, на практике такого не наблюдается, и банковские депозиты пользуются немалым спросом. Это происходит вследствие того, что инвесторы учитывают риски – фактически, зарабатывают на имеющейся информации. То есть, целевую функцию участника финансового рынка можно представить как [1]

(jff^ximi + S({mi})).

R = max

Здесь .S' - энтропия инвестора, которая зависит от планируемого распределения {m j } P=1 его денег по различным финансовым инструментам

,   ,           М!

S({m^ ="'дг^дд;!'                   5)

При больших значениях М (5) в пределе даст (1). С учетом (3) энтропия инвестора включает в себя всю известную инвестору информацию, хеджируя риски.

Для примера, рассмотрим случай, когда инвестор вложил все свои средства mj = М в пирамиду Xj = maXj{Xj}. Тогда использованная им информация равна нулю 5 = In^!/^, = 0, то есть (5) подтверждает разумный вывод, что этот инвестор «жадный» и «не очень умный».

Поскольку энтропия является безразмерной величиной, в (4) появился ключевой параметр /?, являющийся в некотором роде коэффициентом перевода валютных единиц в информацию (он заменяет термодинамический коэффициент перевода энергии в энтропию 1/^ в (3) - обратную температуру). Так, если мы изменим масштаб, и будем считать доход х^т^, скажем, в копейках, то мы необоснованно в сто раз снизим ценность информации S. Поэтому мы должны умножить полученный доход на «ценность» копейки, которая в сто раз ниже, чем у рубля. Можно сказать, ft представляет собой условную «стоимость» рассматриваемого финансового рынка. Это может быть покупательная способность валюты, биржевой индекс, либо иные оценки объективной стоимости анализируемых инструментов рынка [1].

Анализ формулы (4) показывает, что при большой «ценности» активов рынка ft ^ т значение информации нивелируется. Возможно, этим и объясняется то, что крупнейшая в мире финансовая пирамида (фонд Бернарда Мэдоффа) просуществовала на одном из самых развитых финансовых рынков мира по меньшей мере 13 лет, и ущерб от нее превысил 50 миллиардов долларов (только четверть стран мира имеет государственный бюджет свыше этой суммы) [13]. Как только мировой финансовый кризис снизил условную «стоимость» американских рынков ниже некоторого критического уровня ft < ft_c [1], пирамида Мэдоффа мгновенно рухнула.

С другой стороны, в России в середине 90-х годов ценовая характеристика любых финансовых инструментов была ничтожно мала ft ^ 0. Этот период характеризуется полным недоверием населения даже к банковским депозитам. Люди предпочитали хранить деньги и вести расчеты в долларах, имеющих существенно более высокую покупательную способность ft, а также вкладывать деньги в образование детей, в продуктовые запасы – активы, имеющие скорее «информационную» ценность чем «дивидендную», то есть дающие хоть какую-то уверенность в завтрашнем дне.

ЗАКЛЮЧЕНИЕ

В работе рассмотрены вопросы применения энтропии как статистического макропараметра для оценки состояния и анализа динамики финансовых рынков.

Показано, что энтропия является индикатором равновесного положения. При анализе математической модели видно, что приближение к равновесию характеризуется увеличением «размазанности» денежной массы по участникам.

Рассмотрено применение информационной трактовки энтропии. Формула (4) позволяет с позиций теории информации прогнозировать воздействие, которое то или иное сообщение окажет на финансовые рынки. Данный подход является перспективным с точки зрения регулирования динамики финансовых рынков с помощью генерации «нужных» сообщений и информационных сигналов.

Предложен вариант определения справедливой стоимости активов рынка как коэффициента преобразования денежных единиц к информационным. Разработка методологии расчета этого коэффициента в зависимости от планируемых фундаментальных показателей позволит прогнозировать динамику рынка. Возможна постановка обратной задачи: расчет коэффициента на основании текущей статистики распределения инвестиционных средств даст возможность «считывать» с рынка информацию инвесторов для более объективной оценки их настроений.