Информационная система GRVolSU для моделирования дисковых гравитирующих систем

Для моделирования кривых вращения дисковых галактик в 1994 году А.Н. Бурлаком была создана программа Galaxies Rotation (GR), в которой реализованы наиболее востребованные функции для моделирования, но существенным недостатком программы является ее реализация на языке Pascal под операционной системой MS-DOS, что создает большие трудности для ее использования на современной вычислительной технике и не допускает ее модификации. В работе описаны результаты разработки аналога GR, в котором реализованы все ее функции, а так же добавлены новые возможности для моделирования. Востребованность программы GR в научной работе связана с необходимостью построения кривой вращения и ее декомпозиции при построении моделей S-галактик [12; 15; 16]. Декомпозиция кривой вращения с использованием численного динамического моделирования N-тел [5; 10; 19] позволяет получить оценки темного гало [11; 20]. Свойства темного гало в существенной мере определяют динамические процессы в звездном [13], газовом дисках [9] и характеристики спиральной структуры [1]. Для линзовидных галактик (S0) особое значение приобретает корректный учет толщины диска [17; 18].

Данные наблюдений пока не позволяют сделать однозначный выбор в пользу той или иной модели темного гало, поэтому при построении модели кривой вращения важно иметь различные модели гало, не ограничиваясь только квазиизотермическим гало [5], реализованным в GR. В связи с обнаружением значительного числа звездных дисков с неэкспоненциальным профилем поверхностной яркости [7] возникает необходимость строить круговую скорость вращения К(г) с учетом произвольного профиля плотности вещества в звездном диске посредством задания табличных функций.

• 1.    Модели компонент

Круговая скорость зависит от баланса центробежной и гравитационных сил [5]

V 2 (г)      д Ф(г, z = 0)

г            дг где Ф(г, z) — суммарный осесимметричный гравитационный потенциал галактики, определяемый уравнением Пуассона

АФ(г, z) = — 4vGp(г, z),

где p — объемная плотность вещества, определяемая всеми основными компонентами: дисковыми, балджем и гало. Под декомпозицией круговой скорости понимается представление в виде суммы по всем компонентам:

V _c (r) =

м

Е V 2 (г).

г=1

Закон Кинга для плотности балджа р _ь (г) = р _{Ь 0} /(1 + (г/b)²) хорошо описывает наблюдаемые профили яркости балджей на малых расстояниях от центра г . b [8]. На больших расстояниях яркость убывает быстрее, и закон Кинга нуждается в усечении, начиная с некоторого значения г т^ах .

Закон Вокулера для распределения поверхностной яркости в центральной области был получен из наблюдений эллиптических галактик и балджей дисковых галактик [3]. В предположении пропорциональности поверхностной яркости величине поверхностной плотности вещества а имеем а _ь (г) = а _ь0 exp( — 7.67(г/R _e ) ^{1 / 4} ), где а _ь0 — центральная поверхностная плотность балджа, R _e — эффективный радиус, в котором содержится половина массы балджа.

В качестве законов усечения распределений плотности использовались: резкое усечение, линейное усечение, экспоненциальное усечение.

Реализованы следующие модели гало:

• — Квазиизотермическая модель гало с поверхностной плотностью рЦт) = р ₀ /(1 + + (т/а) ² ) [11].

• —    Модель гало Баркета p _h (т) = р ₀ /((1 + т/а)(1 + (т/а) ² )) [2].

• —    Модель гало Наварро-Френка-Уайта построена на основе данных космологических численных экспериментов p nwf (т) = р ₀ /((т/а)(1 + т/а) 2 ) [14].

• —    Модель экспоненциального темного гало р ^н (т) = (М ^н )/(8^а 3 е) • exp ( — т/а) [4].

• —    Логарифмический потенциал гало имеет вид Ф ^ = у ² 1п(т ² + а ² ).

• —    Модель Эйнасто р ^ (т) = р ₀ ехр ( — (2/п ((т/а) ” — 1)).

• —    Профиль распределения плотности вдоль радиуса в модели Ларса Хернкуиста р ^ (т) =

= (М/2^)(а/т)/((т + а) ³ ) [6].

Потенциал для заданной плотности рассчитывается на основе уравнения (2). Важной характеристикой является масса г-компоненты внутри радиуса: М _г (т) = J^<_r ^(£,z) dV .

Для дисковых компонент предусмотрены:

• —    Модель тонкого диска с поверхностной плотностью у(т) = у ₀ exp( — т/т д ) и радиальной шкалой т _д .

• —    Модель толстого экспоненциального диска с распределением объемной плотности р(т,г ) = р ₀ exp( — т/т _д ) ch ^-2 (2/h) с вертикальной шкалой h.

• —    Модель с произвольным распределением поверхностной плотности у ^ = у(т ), j = = 1, ..., m.

• 2. Информационная система

К числу основных входных физических параметров относятся: а, Ь, т т^ах , т _д , h, У о , у _{г 0} . Дополнительным набором параметров является совокупность величин, определяющих численные алгоритмы. В третий набор входят характеристики информационной системы, связанные с представлением результатов моделирования.

Для численного вычисления круговой скорости вращения Vc(т) всей системы и отдельных компонент Vci, объемной плотности вещества р = ^^рг, поверхностной плот- г ности вещества у

= Еу-

масс компонент Мг(т). Для физических величин в ин- г формационной системе принята следующая система единиц: [т] =кпк, [масса] = М0, [скорость] = км/с, [пространственная шкала компоненты] = кпк, [объемная плотность] = М0/пк3, [поверхностная плотность] = М0/пк2.

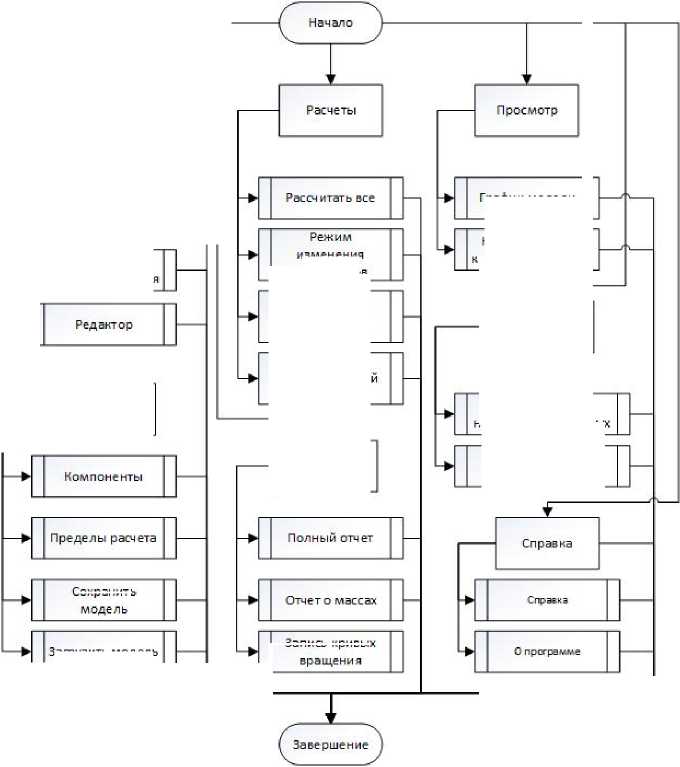
На рисунке 1 представлена диаграмма вариантов использования, отображающая общее представление информационной системы GRVolSU. На рисунке 2 представлена общая блок-схема программы. Каждый блок программы имеет очень сложную внутрен- нюю структуру.

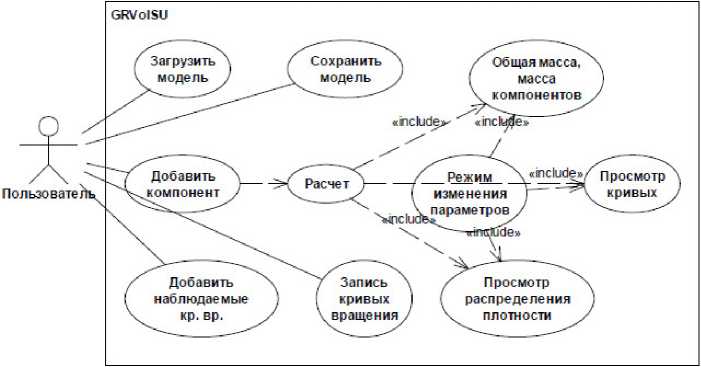
Рис. 1. UML диаграмма вариантов использования

Аппроксимация кривых вращения

Сохранить

Запись кривых

Загрузить модель

Рис. 2. Общая блок-схема

Наблюдаемые кривые вращения

График модели

изменения параметров

Профиль объемной

плотности

Профиль поверхности! плотности

Результаты

Наблюдаемые кривые вращения

Настройка наблюдаемых кривых

Настройка модели

После открытия программы GRVolSU перед вами появляется рабочая область (рисунок 3). Она представляет собой главное окно программы, вверху которой находится набор функций, которые предназначены для выполнения любых задач, связанных с моделированием.

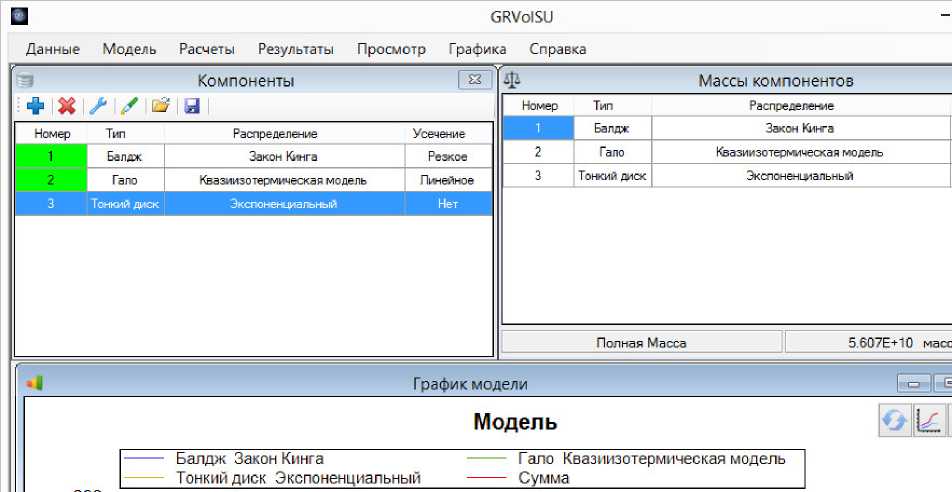
Рис. 3. Рабочая область

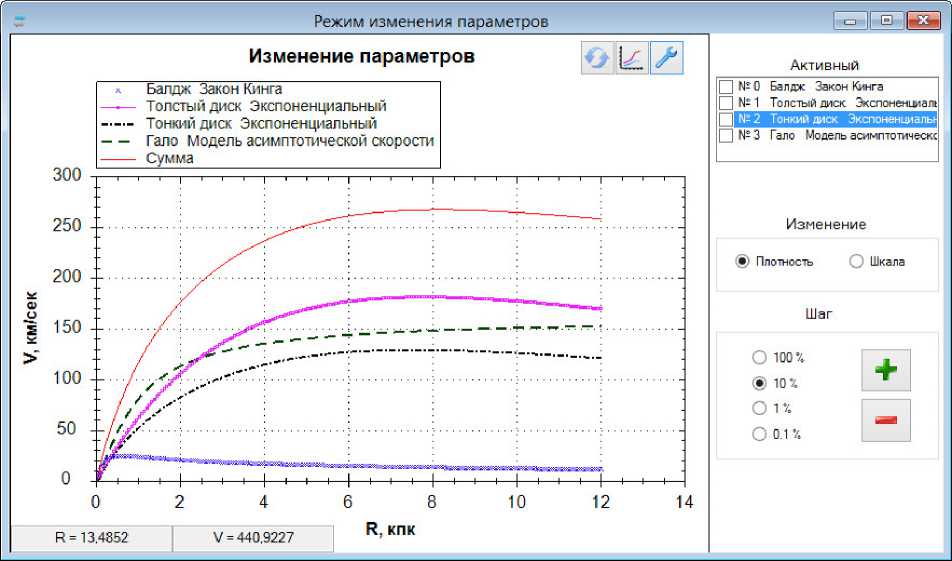
Рис. 4. Режим изменения параметров

Поле «данные» имеет три вложенных функции: наблюдаемые кривые вращения; аппроксимация кривых вращения; редактор. Поле «модель» имеет четыре вложенные функции: компоненты; пределы расчета; сохранить модель; загрузить модель. Функция создания нового компонента, представляет собой диалоговое окно, в котором пользователь, по выбору, определяет тип компонента, модель распределения вещества и закон усечения плотности. Функции загрузки и сохранения модели предназначены для сохранения и загрузки расчетной модели в отдельным файлом формата «.mod». Файл содержит все данные расчета: предел, количество точек, список компонент и их параметры, а так же графические настройки. Поле «расчет» имеет четыре вложенные функции: рассчитать все; режим изменения параметров; профиль объемной плотности; профиль поверхностной плотности.

Поле «результаты» имеет три вложенных функции: полный отчет; отчет о массах; запись кривых вращения. Поле «просмотр» имеет две вложенных функции: график модели; наблюдаемые кривые вращения.

Заключение

Для верификации было проведено сравнение результатов расчетов в системах GRVolSU и GR. Вычисления среднеквадратического отклонения показало для различных компонент различие между GRVolSU и GR порядка 1%. Использование объектноориентированного языка программирования C#, выполняемого в среде .NET Framework, предоставляет для исследователя современный программный продукт с развитым графическим интерфейсом и широким набором галактических компонент. В частности, система GR содержит 1 модель гало, а в GRVolSU реализовано 7 моделей гало. Важным свойством GRVolSU является открытая архитектура информационной системы, позволяющая расширять функционал.