Информационная технология при моделировании задачи горного дела

В народном хозяйстве Республики Казахстан горнодобывающая отрасль промышленности занимает одно из важнейших мест по своей роли в общественном производстве, экономической значимости и социальным факторам. В этой связи для создания эффективных и надежных конструкций шахт и карьеров, развитие системы экологического мониторинга окружающей среды, исследования в области горного дела должны быть комплексными в сочетании фундаментальных и прикладных наук.

В послании Президента Республики Казахстан – Лидера нации Н.А. Назарбаева народу Казахстана «Стратегия «Казахстан-2050» отмечено, что одним из приоритетов является наращивание темпов добычи и поставки на мировые рынки природных ресурсов с тем, чтобы использовать нынешний высокий мировой спрос в интересах страны. Конкурентоспособность горных предприятий в основном обеспечивается при больших объемах добычи полезных ископаемых. Высокопроизводительная их работа достигается на основе внедрения в практику результатов научных исследований по созданию новых и совершенствованию существующих технологических схем с включением техники цикличного и непрерывного действия, рациональная комплектация оборудования, всемерное расширение области применения прогрессивных технологических решений, а также применение совершенных форм организации и управления массовыми горными работами.

Бурное развитие информационных технологий в настоящее время ставит новые требования перед традиционными, вполне сформировавшимися областями знаний, одной из которых является геомеханика и освоение недр. В связи с истощением запасов полезных ископаемых, залегающих на доступных глубинах, основным направлением развития горнодобывающей промышленности будет дальнейшее развитие и совершенствование методов и способов добычи полезных ископаемых с вовлечением в эксплуатацию месторождений со сложными горно-геологическими условиями, большой глубиной разработки и значительным сроком службы бортов карьеров и подземных выработок. Современный уровень развития математического аппарата решения задач геомеханики и вычислительной техники позволяет автоматизировать процесс проектирования выработок, учесть все детали строения массива, добиться большей достоверности проектных решений, обеспечивающих минимальные объемы вскрышных работ, безопасные условия труда, рациональное использование недр и земельных ресурсов, что становится актуальным в условиях рыночной экономики.

Объекты и методы исследований

Горные предприятия в отличие от многих других промышленных объектов и сооружений (металлургических, машиностроительных, химических заводов и др.) являются природнотехнологическими комплексами. Параметры и показатели экономической эффективности горных предприятий определяются для данного уровня техники в основном природными факторами (строением и размерами месторождений, рельефом местности, гидрологическими условиями и др.) и допустимым воздействием их на окружающую среду. Необходимо отметить, что на современном этапе развития горной науки это дифференциация горной науки, возникновение ее новых отраслей и подразделений на базе ее интеграции со смежными областями науки и техники. Поиск и научное обоснование методов рационального и комплексного использования недр обеспечивают их комфортные условия труда и оптимальное состояние природной среды.

Новейший этап в развитии горной науки следует связывать с развертыванием научнотехнической революции (НТР). НТР, как известно, поставила перед человечеством новые проблемы: охрана окружающей среды и истощение минерально-топливных ресурсов. Эти проблемы особенно актуальны для горной промышленности и науки, не решив которые дальнейшее производственное использование полезных ископаемых может стать общественно малоэффективным. Следует заметить, что в районах горных разработок резко ухудшается географическая среда, сильный вред наносит ей способ открытых разработок, увеличение доли которого планируется в ближайшей перспективе. Эффективность способа уже в настоящее время минусуется большими неизбежными расходами на рекультивацию нарушенных разработками земель. Отсюда постановка перед наукой задач принципиального изменения в технологии добычи полезных ископаемых. Это особенно актуально потому, что современная технология не позволяет осваивать месторождения в глубоких недрах земли, а также с низким содержанием полезных ископаемых. Поэтому так актуально разработать принципиально новые методы и средства добычи полезных ископаемых, избежать при этом перемещения масс пустых пород, исключить присутствие под землей человека, резко повысить производительность труда. Это - реальная задача, так как налицо и внутренняя подготовленность и зрелость горной науки для обогащения ее новейшими достижениями фундаментальных наук, на безе которых можно осуществить принципиальный сдвиг в техническом базисе горного производства. В мировой практике технический прогресс, в первую очередь, связан с ориентацией на широкое применение самоходного горного оборудования: разработка самоходного бурового, погрузочно-доставоч-ного и транспортного оборудования, самоходные ковшовые погрузочно-доставочные машины (ПДМ) как с дизельным, так и электрическим приводом. Развитие информационных и коммуникационных технологий, повсеместное внедрение автоматизации и дистанционного управления горными машинами и агрегатами являются приоритетными направлениями совершенствования подземной техники. Дифференциация горной науки на базе ее интеграции со смежными областями науки и техники и в то же время - это синтез горных наук в единую систему знаний для поиска методов рационального и комплексного использования недр, обеспечивающих комфортные условия труда и оптимальное состояние природной среды. Цель горной науки - не только в описании, объяснении условий средств и способов разведки добычи и первичной переработки полезных ископаемых, но главным образом в поиске путей их совершенствования и изменения для облегчения условий труда и повышения экономичности производства. Горная наука сегодня - это сложный, развивающийся комплекс научных дисциплин. Все процессы и явления, происходящие при разведке, добыче и переработке полезных ископаемых, содержат внутренние и внешние противоречия, открытие, исследование и разрешение которых является главной задачей горной науки.

Горные науки по уровню исследований и методам решения задач существенно отличаются от таких фундаментальных наук, как физика или химия, которые используют для решения стоящих перед ними задач количественные методы. В основе решения задач, стоящих перед горным наукам - качественное изучение объектов исследования. Очень часто в практике используются статистическое накопление факторов и их субъективная оценка, которая базируется на методе аналогий. Это можно объяснить тем, что объекты горной науки представляют собой конкретные условия, для которых трудно установить законы, "общие для всех мест и времен". Общая тенденция математизации наук не обошла и горные науки, но для решения большинства крупных горных проблем на сегодня недостаточно математических средств, поскольку задачей, например, разработки месторождений является создание самоорганизующихся многофакторных систем, а в дальнейшем и самопрограммируюших автошагов. На современном этапе количественно решать задачи, возникающие, например, при разработке полезных ископаемых, можно только применительно к определенным, идеальным месторождениям. Поэтому для придания практического значения таким "количественным" решениям допущения, лежащие в основе анализа, должны, в соответствии с принятыми величинами, согласовываться с естественными условиями.

Результаты и обсуждения

В процессе образования в массиве открытых или подземных горных выработок нарушается естественное напряженно-деформированное состояние. Вокруг выработок различного назначения появляются зоны неупругих деформаций. Особенно важное значение имеют закономерности деформирования горных пород за пределы прочности, связанные с разрыхлением (необратимым увеличением объема), разупрочнением (снижением сопротивляемости) и упрочнением. Указанные закономерности в значительной мере определяют характер напряженно-деформированного состояния породного массива вблизи выработок, особенно при комбинированной разработке месторождений полезных ископаемых открытым и подземным способами во взаимном влиянии друг на друга. Сложность горногеологических и горнотехнических условий, их большое разнообразие, отсутствие комплексных методов оценки свойств и состояние породного массива ставит перед геомеханикой (наука о механическом поведении породного массива под действием тектонических сил и производственной человеческой активности) все новые проблемы. При этом одной из важнейших является проблема разработки общей методологии и метода, учитывающих вышеназванные особенности, на основе современного достижения в области численных методов математики, механики твердого деформируемого тела (теории пластичности и разрушения) и информационных технологий.

Запишем закон Гука для условий плоской деформации ( е ₂ = 0) в следующем виде:

0" 1 = £ . (£ , ■ v , Е э )/(1- v)

О з = ^ п (Е з + V , £ 1 )/(1- v²J,              (1)

где ЕП,пП - «плоские» аналоги модуля Юнга Е и коэфициента Пауссона  п, связанные с ними соотношениями: Еп, =Е/(1-v2), пп=v/(1-v).

Считая, что предел прочности рассматриваемой среды в области сжатия описывается критерием Кулона:

О 1 = S + O 3 ctg5,                        (2)

где 5 = 2cctg(^/4 — ^/2) - прочность на одноосное сжатие; ctg5= (1+sinф)/(1-sinф); с,ф - сцепление и угол внутреннего трения.

В области растяжения дополним критерием о3= Т, Т - прочность на растяжение. После несложных преобразований получим описания границ прочности через главные деформации - сжатия считаются положительными:

[(Е п £ 1 - S) (1 - V n Otg5)/( ctg5 - V n )-V n S] / Е п - £ з =0                                          (3)

T(1- v^)/ Е п - V n E i - £ 3 = 0                   (4)

В координатах £ 1 и £ 3 уравнения (3) и (4) имеют вид соответственно прямых А'В' и D'A' (рис. 1,a). Таким образом, в области 1 в пределах контура D'A'B' по известным деформациям £ 1 и £ 3 напряжения С 1 и ц₃ могут быть найдены по формулам (1). За пределами контура A'B'C' действуют иные уравнения связи деформаций и напряжений.

Пусть в процессе нагружения деформированное состояние элемента среды вышло в некоторую точку Е ′ на границе зоны упругости (рис. 1). Рассмотрим закономерности дальнейшего пластического деформирования, протекающего при постоянном минимальном главном напряжении. Увеличение деформации £ 1 (т.е. укорочение элемента среды в направлении £ 1 ) сопровождается уменьшением деформации £ 3 (расширением в перпендикулярном направлении). Полный вектор пластических деформаций £_р состоит из двух компонентов: £_1р и£ зр , а взаимосвязь этих компонентов определяется принятым законом течения (рис. 1).

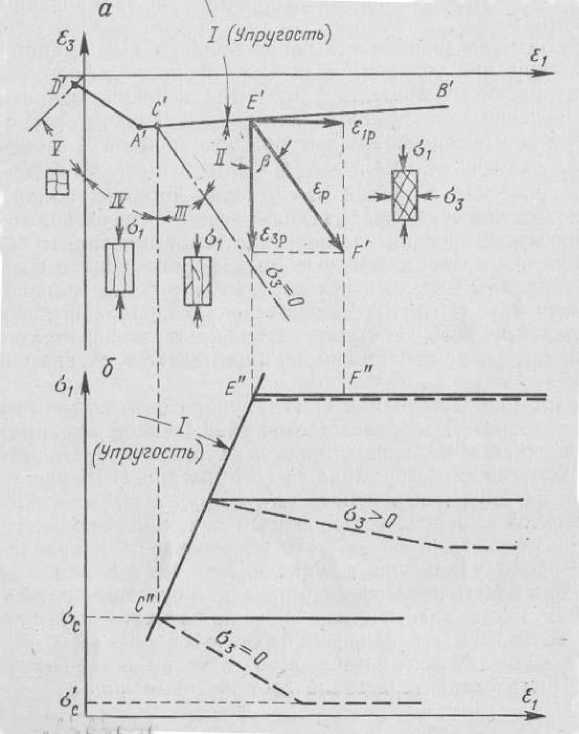
Рисунок 1 - Закон состояния среды

Если принять £ з _р = -£_1р , то укорочение в направлении £ 1 будет равно удлинению в направлении £ 3 , а объем элемента среды при пластическом деформировании будет оставаться неизменным. Такое пластическое течение может быть названо равнообъемным. В более общем случае связь компонентов пластических деформаций может быть охарактеризована соотношением вида

^£ 3р      ctgP^£ ip .                        ⁽⁵⁾

Угол Р на рисунке 1,a определяет степень разрыхления при пластическом течении; величина ctgP может быть названа коэффициентом дилатации. При Р = 5 формула (5) соответствует принципу нормальности (ассоциированному закону течения).

При этом, если деформации элемента среды £ 1 и £ 3 характеризуют точку F' на рисунке

• 1,a, то они могут быть представлены в виде суммы упругих и пластических компонентов:

• ^£ 1 = ^£ 1 е +^£ 1 р ;^ 3 = ^£ 3 е +^£ 3 р (6)

Упругие компоненты £ 1 и £ 3^ являются координатами точки Е' и определяются из формул упругости (1) при подстановке в них значения 7 1 на границе упругости по формуле Кулона (2). Подставив полученные таким образом значения е_1е и £ 3 и величину £ 3^ из формулы (5) в уравнения (6), получим систему двух уравнений, решив которые относительно 7 3 и £ 1 , найдем величину напряжения 7 3 соответствующую данному деформированному состоянию:

7 3 =[ Е п ⁽£ 1 + £ 3 ) + S (п п - 1)]/(1-V H Otg5 +ctg5 -п п ) (7)

Для определения величины 7 1 должно быть задано семейство графиков связи 7 1 и £ 1 при пластическом деформировании в условиях 7₃ = const (рис. 1,б). Если в процессе деформирования сопротивляемость остается постоянной (идеальная пластичность), то графики 7 1 - £ 1 имеют вид горизонтальных прямых (сплошные линии на рисунке 1,б), а сама величина 7 1 может быть рассчитана по ранее определенной величине 7 3 с помощью формулы (2).

Для пород, разупрочняющихся в процессе запредельного деформирования, может быть предложено [3], например, семейство графиков, изображенных на рисунке 1,б штриховыми линиями. Эти графики характеризуют среду, сопротивляемость которой в процессе пластического деформирования снижается от исходной величины, определяемой по формуле (2), до остаточной величины

7 1 =min [(S + 7 3 ctg5), (S' + 3 0tg5')], (8)

где S' и5' - характеристики остаточной прочности (S'' < 5).

Разработанные модели реализованы в виде численных процедур для случаев плоской деформации в деформационном варианте теории пластичности на основе метода конечных элементов.

Основная процедура метода конечных элементов рассматривает среду как упругую и сводится к решению системы линейных алгебраических уравнений относительно неизвестных перемещений :

,

• где     - матрица жесткости системы;

• - вектор узловых сил.

Поскольку исследование напряженно-деформированного состояния породного массива с учетом запредельной деформируемости представляет собой нелинейную задачу, в работе нами получены новые разработки в области комбинированной процедуры применительно к общему случаю, когда закон состояния среды задается на основе предложенной модели. Отладка программы, проверка качества конечно-элементной сетки и геомеханической модели породного массива осуществлены решением тестовых задач, имеющих аналитические решения.

Для количественной и качественной оценки решения МКЭ по разработанной программе проведено решение, сопоставимое с классической задачей Галина. Заданы свойства идеально-пластической среды с критерием текучести Треска. Численные характеристики:

Мпа,            ,         ,

Мпа,       . Коэффициент дилатации      , что обеспечивает равнообъемное течение.

Для того чтобы выяснить характер роста зоны пластических деформа ц ий с изменением нагрузки, задача решалась в двух вариантах. В первом варианте нагрузка σ y =3МПа и σ x =2,4 МПа прикладывалась целиком, во втором задавалось приращениями в пять ступеней. Результаты расчетов по вариантам, соответствующим полной нагрузке, совпадают. На рисунке 2 показаны перемещения точек контура выработки U, рост зоны пластических деформа ц ий. По полученному решению контур пластической зоны представляет собой эллипсоподобную фигуру с большой полуосью а=3,14R и малой полуосью b=1,77R (R-радиус отверстия). Из решения Галина следует, что зона пластических деформа ц ий имеет вид эллипса с полуосями а=3,05R,  b=1,64R.

Напряжение вблизи контура отверстия равны пределу прочности на одноосное сжатие, а вдали от контура на поверхности - заданным напряжениям.

Рисунок 2 - Перемещения точек контура выработки U и рост зоны пластических деформа ц ий.

В таблице 1 приведена величина перемещения узлов контура – отверстия в долях R, а в таблице 2 - значения напряжений в пластической зоне, полученные по формулам

Галина и по МКЭ. Из таблицы следует, что даже при сравнительно крупной сети элементов аналитическое и численное решения очень близки.

Таблица 1 - Величина перемещения узлов контура – отверстия

Номер узла	1	2	3	4	5	6	7	8	9	10	11
Δ x 103/R	-41	-40	-38	-34	-29	-24	-18	-12	-6	-4	0
Δ y 103/R	0	-9	-16	-23	-29	-32	-36	-38	-39	-39	-39

Таблица 2 - Значения напряжений в пластической зоне

Горизонтальная ось					Вертикальная ось
r/R	по Галину	по МКЭ	по Галину	по МКЭ	r/R	по Галину	по МКЭ	по Галину	по МКЭ
1	0	0.1	2	2.07	1	0	0	2	2.08
1.28	0.49	0.49	2.49	2.62	1.14	0.27	0.39	2.27	2.39
1.8	1.18	1.20	3.18	3.37	1.28	0.49	0.58	2.49	2.58
2.14	1.52	1.50	3.52	3.60	1.64	0.99	1.10	2.99	2.88
2.57	1.89	1.85	3.89	3.92
3.05	2.23	2.19	4.23	4.24

Заключение

В заключении необходимо отметить, что разработанные процедуры и программы позволяют решать с помощью современных компьютеров широкий класс задач горного производства, в которых требуется определять напряженно-деформированное состояние породного массива, ослабленного выработками в разных горнотехнических и горногеологических условиях. Компоненты естественного поля напряжений представляются в виде зависящих от геомеханических структур месторождения, и в программе учитываются с помощью граничных условий. При этом граничные условия могут быть заданны в виде нулевых или ненулевых узловых сил или перемещений (или же смешанных условий). Неоднородность массива учитывается по моделям путем введения различных прочностных и деформационных характеристик E, v, у, с, р (модуль упругости, коэффициент Пуассона, плотность, сцепление и угол внутреннего трения). Поверхности ослабления и нарушения в массиве имитируются слоями элементов с соответствующими пониженными прочностными свойствами.