Информационно-математическая система раннего предупреждения об аварийной ситуации

Алешина Анна Александровна, аспирант кафедры «Прикладная математика и информатика».

Кравцов Юрий Андреевич, аспирант кафедры «Прикладная математика и информатика».

ты разработана информационно-математическая система, включающая блок прогнозирования состояния объекта по результатам решения системы временных рядов, а в условиях стабильной работы – блок оценки стабильности с помощью многомерных контрольных карт.

Моделирование и прогнозирование системы временных рядов по показаниям датчиков основано на методике структурно-параметрической идентификации системы, реализованной на основе подхода адаптивного регрессионного моделирования [1 - 3], предусматривающего при построении моделей временных рядов последовательную адаптацию модели к возможным нарушениям основных предположений регрессионного анализа.

Рассмотрим технический объект, состояние которого характеризуется параметрами, значения которых регистрируются через определенные промежутки времени и образуют многомерный временной ряд, представляемый в виде системы y ¹ ( t ), y² ( t ), „., y^N ( t ) . Предполагается,что одномерный временной ряд yⁱ (t) , наблюдаемый в равноотстоящие моменты времени t 1 , t 2 , .., t n , может быть представлен в виде суммы функций:

У i (t) = f i ( t ) + g¹ ( t ) + V i ( t ) + E i ( t ), ⁽¹) при этом функция f ⁱ(t) – неслучайная (долговременная) функция тренда соответствующего ряда; g ⁱ (t) – неслучайная периодическая функция – совместная гармоническая составляющая ряда; ^ (t) — случайная с элементами регулярности функция - векторная авторегрессия; e ⁱ(t) – нерегулярная компонента (случайная величина, ошибка).

На первом этапе для системы временных рядов выполняется разведочный анализ (фрактальный, мультифрактальный) для выявления степени регулярности каждого ряда системы. При выявлении заметной трендоустойчивости для соответствующих рядов выделяется функция тренда f(t) , которую обычно приближают полиномом достаточно низкой степени. Оптимальная функция трендовой составляющей ищется по критерию минимума внешнего среднеквадратического отклонения.

Дальнейшее сглаживание временного ряда производится методами совместного гармонического анализа. Для каждого ряда методом пошаговой регрессии находятся значимые гармоники. После выделения регулярных составляющих целью анализа системы временных рядов является моделирование остатков случайной с элементами регулярности функцией ^ (t) . Функция ^ (t) для системы взаимосвязанных рядов может быть представлена в виде модели векторной авторегрессии. Иногда для оценки параметров модели (1) эффективно использование псевдоградиент-ного метода [4].

В итоге получаем для каждого из N временных рядов комплексную модель, содержащую регулярную составляющую (тренд, гармоники) и векторную авторегрессию. После структурнопараметрической идентификации системы проверяется соблюдение условий применения регрессионного анализа. Если основные предположения соблюдаются, построенные комплексные модели системы временных рядов могут быть использованы для прогнозирования, в противном случае проводится соответствующая процедура адаптации к нарушению данного предположения [1].

Методика структурно-параметрической идентификации реализована в виде блока программного комплекса, предназначенного для построения моделей системы взаимосвязанных временных рядов с последующим их использованием для прогнозирования состояния и обнаружения нарушений процесса до того, как контролируемые параметры вышли за предельные значения.

Ниже представлены комплексные модели системы временных рядов, полученные по результатам наблюдений восьми датчиков вибраций гидроагрегата в режиме запуска (использовано 76 наблюдений).

у 1 (t) = 6,249 • t + 4,477 • sin(2^t / 84) + 40,006 х х sin(2^z / 42) + 0,950 • у i (t — 1) — 0,016 • у 2 (t — 1) + + 0,058 • у 7 (t — 1) — 0,108 • у 8 (t — 1) + ^i (t), у 2 (t) = 6,265 • t + 4,477 • sin (2^7 / 84) + 440,006 х х sin(2^t / 42) — 0,010 • у 1( t — 1) + 0,938 • у 2 (t — 1) + + 0,066 • у7 (t — 1) — 0,061 • у8(t — 1) + в2 (t), у3 (t) = 15,036 + 4,477 • sin(2nt /84) + 36,386 х х sin (2^t / 4,941)+ в 3( t), у 4(t) = 4,477^ srn(2M /84) + 440,006^ srn(2M /42) + + 0,966^ у 4 (t — 1) + 0,406^ у 5 (t — 1) + 0,003^ у 7 (t — 1) — — 0,534^ у 8( t — 1) + e4( t), у 5 (t) = 34,798+ 4,477^ sin(2M/84) + 44()006х х sin(2M / 42) + 0,981- у 5(t — 1) + 0,312- у 8 (t — 1) + в5 (t), у 6 (t) = 1436,810 — 20,836 • t + 4,477 • sm(2^z / 84) + + 440,006 • sin(2^t / 42) + 0,976 • у 6( t — 1) —

— 0,321 у 8( t — 1) + в 6( t), у 7( t) = —6,715 • t + 4,477 • Sin(2^t / 84) + 440,006 х х sin(2^t / 42) + 0,179 • у 4( t — 1) +1,782 • у 5( t — 1) + + 0,835 • у 7( t — 1) + 2,270 • у 8( t — 1) + в7 (t), у 8 (t) = 4,477 • sin(2^t / 84) + 363,862 • sin(2^t /28) + + 0,979 • у 8( t — 1) + в8( t).

Качество полученной модели позволяет прогнозировать состояние гидроагрегата на 7-8 наблюдений (10% от выборки наблюдений). На рис. 1, а показан смоделированный временной ряд для канала №1, а на рис. 1, б - соответствующий прогноз на 8 наблюдений. Сплошной линией показаны опытные данные, штриховой – расчетные.

В режиме стационарной работы агрегата состояние объекта часто считается аварийным, если нарушена стабильность процесса. При контроле технологических процессов общепринятой является проверка стабильности процесса с использованием контрольных карт. Для контроля независимых параметров процесса используется контрольная карта Шухарта [5]. При наличии коррелированных параметров применяются многомерные карты Хотеллинга [6].

Решение о том, какие карты использовать для оценки стабильности процесса, принимается на основе оценки корреляций между параметрами и проверки их значимости. С этой целью на этапе анализа процесса работы агрегата берется обучающая выборка, которая используется для оценки степени взаимосвязи контролируемых параметров и определения характеристик используемых контрольных карт.

О нарушении стабильности процесса при использовании контрольных карт, как правило, свидетельствует выход исследуемой статистики за контрольную границу. Для одномерных карт предложен ряд методов повышения их эффективности (под эффективностью понимается чувствительность карты к возможному нарушению ста-

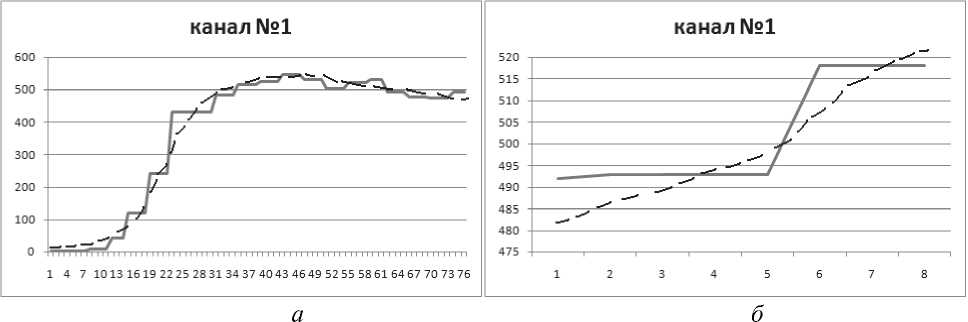
Рис. 1. Моделирование ( а ) и прогнозирование временного ряда ( б )

бильности процесса). Предлагается чувствительность карты Хотеллинга также повысить путем использования предупреждающей границы, а также путем выявления неслучайных структур специального вида [7, 8].

В модифицированной карте Хотеллинга вводится дополнительно предупреждающая граница; область возможных значений контролируемой статистики разбивается при этом на три непере-секающихся подмножества: 1) область , в которой процесс статистически управляем, 2) область , в которой процесс находится в “переходном” состоянии (в зависимости от того, как определяется положение предупреждающей границы, нахождение нескольких точек в этой области может свидетельствовать о нарушении процесса), 3) область, в которой происходит нарушение процесса.

Случай, при котором попадание двух точек подряд в предупреждающую область, свидетельствует о выходе процесса из-под контроля, рассмотрен ранее. Использование предупреждающих границ повышает чувствительность карты в диапазоне наиболее важных с практической точки зрения смещений до 23% [5]. Представляет интерес ситуация, при которой о выходе процесса из-под контроля свидетельствует попадание в предупреждающую область трёх или четырех точек. Результаты расчета положения предупреждающих границ, проведенного методами теории марковских цепей, приведены в таблице 2.

На рис. 2 показаны возможные типы неслучайных структур на карте Хотеллинга:

• а)    тренд (сколько точек подряд на возрастание или на убывание в зависимости от количества контролируемых параметров может рассматриваться как неслучайная структура, т.е. вероятность появления такого количества точек соизмерима с вероятностью ложной тревоги);

• б)    приближение к оси абсцисс (зона С: в диапазоне до 1/3 Т ² _кр ) – сколько точек, расположенных в этой зоне, в зависимости от количества контролируемых параметров может рассматриваться как неслучайная структура,

• в)    приближение к контрольной границе (зона А),

• г)    резкие скачки на карте – на величину kТ ² _кр , k = 0,6 ё 0,9… – при каком k при заданном количестве контролируемых показателей р соответству-

• Таблица 1. Положение контрольной и предупреждающей границ карты Хотеллинга

Количество контролируемых параметров р	Количество точек между предупреждающей и контрольной гран ица ми k	Положение ко нтрольной границы UCL	По ложе ние предупреждающей границы UWL
2	2	12,39	5,70
	3	13,29	3,60
	4	14,10	2,55
3	2	14,89	7,44
	3	15,35	5,12
	4	15,60	3,87
5	2	19,48	10,52
	3	20,79	7,70
	4	21,19	7,64
10	2	28,40	17,61
	3	28,97	13,94
	4	30,08	12,08

Структура	Критическое сост оян ие при заданном количестве конт ролируем ых па рам етров
	2	3	4	5	6	7	8	9	10
Тренд	6 точек	6 точ ек	6 точек	6 точек	7 точек	7 точек	7 точек	7 точек	7 точе к
Приближение к оси абсцисс	-	-	15 точек	12 точек	10 точек	9 точек	8 точек	7 точек	6 точе к
Приближение к контрольной границе	2 точки из 5	2 точки из 3	2 из 3, или 3 из 10	2 из 3, или 3 из 9	3 из 8, или 4 из 15	3 из 7, или 4 из 14	3 из 6, или 4 из 13	3 из 6, или 4 из 12	3 из 6, или 4 из 11
Резкие скачки	k = 0, 75	0,75	0,70	0,70	0,70	0,70	0,65	0,65	0,65
Цикличность	8 точек	9 точ ек	9 точек	9 точек	9 точек	10 точек	10 точек	10 точек	11 точе к

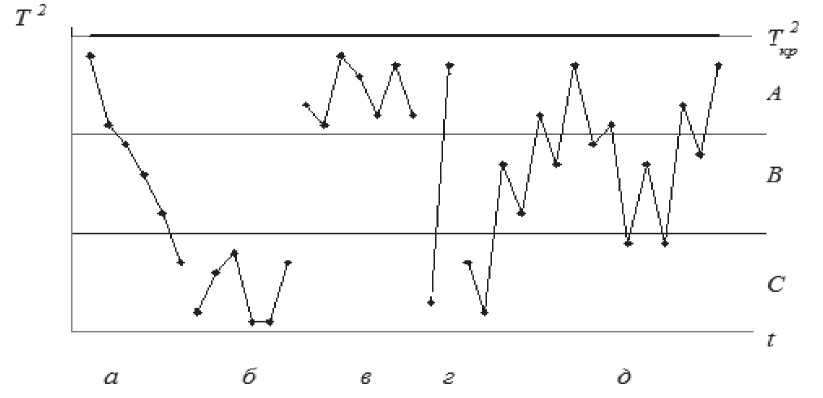
Рис. 2. Типы неслучайных структур на карте Хотеллинга

Таблица 2. Характеристики неслучайных структур на карте Хотеллинга

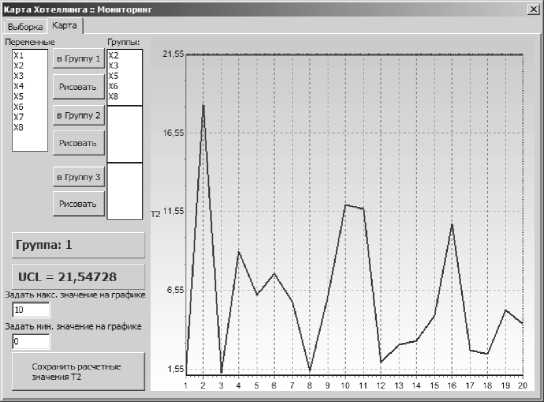
Рис. 3. Карта Хотеллинга при мониторинге процесса: в выборках 1-2 и 2-3 имеют место резкие скачки

ющий скачок на карте может рассматриваться как неслучайная структура,

• д)    цикличность (сколько точек, расположенных в шахматном порядке, может рассматриваться как неслучайная структура?).

Представляет интерес расчет вероятностей появления структур заданного вида на конт- рольной карте Хотеллинга: если эта вероятность имеет тот же порядок, что и заданный уровень значимости, то соответствующая структура не может считаться случайной, и ее появление на контрольной карте свидетельствует о нестабильности процесса. В табл. 2 приведены результаты расчета, позволяющие выявить наличие неслу- чайной структуры на карте, и таким образом, сделать заключение о нестабильности процесса.

В качестве примера на рис. 3 показана контрольная карта Хотеллинга при мониторинге вибраций гидроагрегата: выходов точек за контрольную границу нет, однако в выборках 1-2 и 23 имеют место резкие скачки на величину, большую 0,70 Т ² _кр , что свидетельствует о нарушении стабильности процесса и возможной аварийной ситуации.

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.B37.21.0672 (федеральная целевая программа “Научные и научно-педагогические кадры инновационной России”).