Информационно-образовательная предметная среда как необходимое условие повышения уровня математической подготовки в вузе

Анализ современного состояния математической подготовки школьников и студентов педагогических вузов естественнонаучного направления выявил следующие проблемы:

• -    низкий уровень сотрудничества между кафедрами общепрофессиональных и специальных дисциплин;

• -    отсутствие связи между программами по математике для старшеклассников естественнонаучного профиля и для студентов первого курса факультета естествознания педагогического вуза;

• -    недостаточное количество учебно-методических материалов по математике, соответствующих потребностям будущей профессиональной деятельности школьников и студентов;

• -    отсутствие (практически полное) единой системы контроля знаний школьников и студентов.

Решить эти проблемы можно посредством отбора содержания дисциплины и организации процесса обучения математике на основе:

• -    модели интеграции школы и вуза, причем стержневым элементом интеграции должен быть вертикальный принцип научной и учебной деятельности школьников, студентов и преподавателей;

• -    вертикальной модели непрерывной математической деятельности школьников и студентов, основанной на применении математических методов в химии;

• -    концентрического подхода к отбору содержания математики на основе тезаурусного механизма на всех уровнях обучения;

• -    информационно-образовательной предметной среды.

На основе предложенной модели интеграции школы и вуза [1], вертикальной модели непрерывной математической деятельности школьников и студентов [4], а также анализа научнометодической литературы, диссертационных исследований по вопросам преемственности и непрерывности обучения математике, требований общества к обновлению компонентов математической подготовки [3], собственного опыта работы была построена структурно-логическая модель непрерывной математической подготовки школьников и студентов этой категории (рис. 1).

В соответствии с представленной структурно-логической моделью была спроектирована информационно-образовательная предметная среда математической подготовки в системе «школа - вуз».

Под информационно-образовательной предметной средой, как и И.В. Роберт [5], мы понимаем совокупность условий, способствующих возникновению и развитию следующих процессов:

• -    активного информационного взаимодействия между преподавателем, обучаемым (обучаемыми) и информационными и коммуникационными технологиями, ориентированного на выполнение разнообразных видов самостоятельной деятельности с объектами предметной среды, в том числе информационно-учебной, экспери ментально-исследовательской деятельности, осуществляемой с помощью компонентов среды;

• -    функционирования организационных структур педагогического воздействия в рамках определенной технологии обучения.

Вопросам разработки информационной среды посвящены труды Б.Л. Агранович, Б.Н. Богатыря, Г.Ю. Беляева, Ю.С. Брановско-го, Я.А. Ваграменко, И.Г. Захаровой, Н.А. Иньковой, Т.Н. Казариной, Э.Г. Скибицкого, А.В. Хуторского и др.

Однако большинство исследователей рассматривают общетеоретические аспекты построения информационной среды, практически не затрагивая вопросы создания и использования еди- ной информационно-образовательной предметной среды по математике в системе «школа - вуз».

Предложенная нами среда предполагает объединение информационных, материальных, технических и интеллектуальных ресурсов школы и вуза, создание единой ресурсной среды, обеспечивающей преемственность школьных и вузовских учебников по математике, универсальность контроля и диагностики знаний школьника и студента, организацию непрерывной исследовательской деятельности обучающихся.

Информационно-образовательная предметная среда включает субъективный, ресурсный и технологический компоненты.

Субъектный компонент определяет взаимоотношения между участниками образовательного процесса. Личностно ориентированный подход к обучению и информатизация образования предполагают взаимодействие обучающихся как между собой и с обучающим, так и с информационными ресурсами с помощью информационных и коммуникационных технологий.

Ресурсный компонент состоит из двух комплексов.

• 1 . Система интегрированных курсов «Математические методы в химии» в печатном и электронном видах. Данный комплекс включает:

• -    предпрофильный элективный курс «Введение в математическую химию», в котором даются общие представления об использовании математических понятий и методов при решении прикладных и профильных задач;

• -    профильный элективный курс «Введение в математическое моделирование химических процессов», в котором даются основные теоретические понятия метода математического моделирования химических процессов и решаются задачи (большинство из которых рассмотрено в предыдущем

  

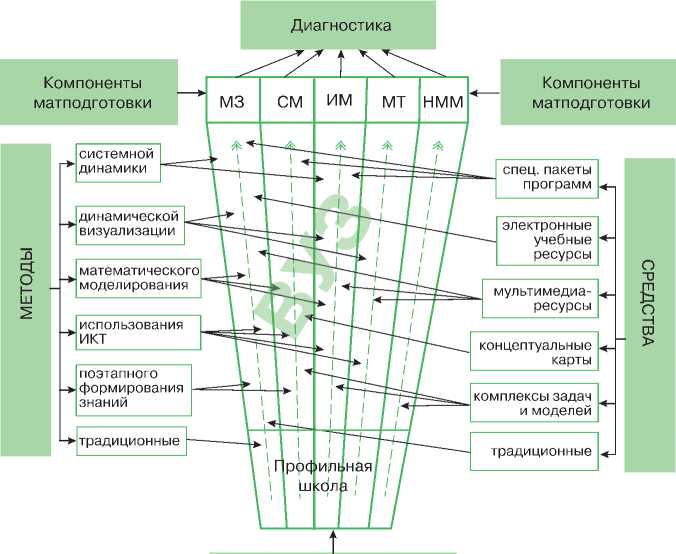
  Отбор содержания

  Рис.1. Структурно-логическая модель непрерывного обучения математике (компоненты математической подготовки: М3 - математические знания, СМ - системное мышление, ИМ - интуитивное мышление, МТ-математический тезаурус, НММ-навыки математического моделирования) Примечание. ИКТ- информационно-коммуникационные технологии.

  
  

курсе) с позиций математического моделирования. Основной математический материал, использующийся в решении этих задач, относится к разделу «Элементарная математика».

• -    факультативный курс «Математика. Подготовка к единому госэкзамену». Так как независимо от выбранного профиля учащиеся сдают единый госэкзамен по математике, поэтому нами предусмотрена программа подготовки к сдаче этого экзамена;

• -    факультативный курс (для школьников) и курс по выбору для студентов факультета естествознания педагогического вуза «Математическое моделирование химических процессов». Программа данного курса опирается на цикл математических, общенаучных и профессиональных дисциплин, таких как: математический анализ, геометрия и линейная алгебра, информатика, общая и физическая химия, термодинамика. Это позволяет использовать достаточно разнообраз

• 2 . Электронный учебно-методический комплекс по линейной алгебре для студентов факультета естествознания педагогических вузов. Он содержит:

• -    электронный учебник по линейной алгебре, основанный на трехмерном тексте и использующий уровневые подсказки;

• -    электронную энциклопедию по линейной и векторной алгеб-

  
  
  

ные математические теории для построения математических моделей рассматриваемых концепций естественных наук с активным использованием информационных технологий.

Эта система интегрированных курсов способствует развитию осознания ключевых понятий математики и химии, предусматривает формирование знаний и умений по применению методов математического моделирования химических процессов в решении профильных задач, обеспечивает преемственность и непрерывность обучения математике.

зации информации и знаний, поэтапного формирования знаний, проектно-исследовательские методы, а также математическое моделирование, непрерывное использование информационных и коммуникационных технологий.

Суть метода системной динамики заключается в создании в сознании человека интуитивных картин поведения объектов или систем реального мира. Применение данного метода способствует развитию чувственной памяти и интуитивного типа мышления.

Основным средством метода системной динамики является визуализация. Технология визуализации учебной информа- ре, состоящую из видеороликов, позволяющих визуализировать математическую информацию, включая понятия и вычисления;

• -    компьютерные тесты по линейной, векторной алгебре и математическому моделированию, основанные на тезаурусном подходе;

• -    построенные концептуальные карты по математике, химии и интегрированные карты «математика - химия», показывающие связь математики с химией и осуществляющие динамическую визуализацию интегрированного тезауруса.

Система контроля качества математического образования включает критерии и показатели уровня математической подготовки обучающихся. В нашем исследовании для проведения контроля(промежуточного и итогового) мы используем тезаурусный подход. Для оценки качества математической подготовки при итоговом контроле выделены три уровня в соответствии с теорией поэтапного формирования умственных действий.

Первый уровень - базовый. Он означает, что студент усвоил базовые математические знания, умения и навыки.

Второй уровень - компетент-ностный. Он характеризует умение применять математические знания в профильной деятельности.

Третий уровень - творческий. Он подразумевает, что студент способен решать сложные нестандартные задачи профильной сферы.

Уровень обучения математике определяется по сумме баллов, полученных при прохождении построенных электронных тестов, выявляющих уровень (в соответствии с государственными образовательными стандартами высшего профессионального образования) сформированности математического тезауруса, а также известных в литературе психологических тестов (тест Амтхауэра) по определению уровня сформированности системного и интуитивного мышления.

Технологический компонент в соответствии со структурой методической системы объединяет методы, средства и формы обучения.

Основными принципами технологического компонента являются преемственность и иерархическая непрерывность процесса математической подготовки.

В исследовании, наряду с традиционными методами обучения, выделены методы системной динамики и динамической визуали- ции - это система, включающая в себя следующие слагаемые: комплекс учебной информации, визуальные способы ее предъявления, визуально-технические средства передачи информации, набор психологических приемов использования и развития визуального мышления в процессе обучения. Для визуализации математической информации наиболее эффективными с позиций информационного подхода являются построение концептуальных карт и использование анимаций. Визуализация учебного материала позволяет сформировать образы абстрактных математических понятий, повысить степень запоминания на интуитивном уровне, представить целостную картину применения математических методов в профильной деятельности.

Математическое моделирование используется для обеспечения профильной интегрированности и прикладной направленности процесса обучения математике, снижения уровня математических абстракций. Введение метода математического моделирования способствует развитию системного, алгоритмического и интуитивного мышления. Основные средства данного метода - про- граммы для компьютерного моделирования объектов и явлений.

Теория поэтапного формирования умственных действий П.Я. Гальперина на первое место ставит анализ усвоения действий, рассматривая знания как образования, производные от действий и их усвоения. Этот метод способствует формированию у студентов системных знаний и начальных навыков системного мышления.

Говоря о проектно-исследовательском методе, мы имеем в виду способ достижения дидактической цели через детальную разработку реальной проблемы, которая должна завершиться определенным практическим результатом, оформленным тем или иным способом с использованием информационных технологий.

Требования информационного общества обуславливают необходимость непрерывного использования компьютерных технологий в учебном процессе. В зависимости от цели занятия и формы организации используются программы для построения концептуальных карт, специализированные математические и профильно-математические пакеты программ, электронные таблицы, электронные обучающие программы и учебники, интернет -технологии.

Результаты проведенного анализа существующих форм представления учебной информации показали, что электронные учебные материалы необходимо строить с использованием визуализации математических понятий, динамических образов для формул и вычислений, многоуровневых подсказок, концептуальных карт.

Более 50% учебного материала отводится сегодня для самостоятельного изучения, поэтому организацию самостоятельной работы студентов естественнонаучного направления педагогического вуза при изучении математики мы проводим на основе предло- а о

л ^

ЧА

ч

• ■    Контрольная группа

• ■    Экспериментальная группа

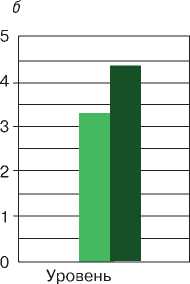
Рис 2. Результаты прохождения тестов: а -б - итоговый результат обучения математике женной модели самостоятельного изучения учебного материала [2]. Эта модель основана на активном использовании информационных и коммуникационных технологий, контекстного подхода, методов математического моделирования и проектно-исследовательской деятельности.

С 2008 по 2011 год проводился педагогический эксперимент по обучению математике учащихся естественнонаучного направления некоторых школ Красноярска, факультетов довузовской подготовки и естествознания Красноярского государственного педагогического университета им. В.П. Астафьева в условиях информационно-образовательной предметной среды. Результаты эксперимента представлены на рис. 2.

Полученная опытно- экспериментальная оценка позволяет сделать вывод о том, что обучение студентов естественнонаучного направления педагогического вуза математике в условиях информационно- образовательной предметной среды повышает уровень математической подготовки за счет обеспечения преемственности и непрерывности обучения математике, использо

X

математической подготовки

по компонентам математической подготовки;

вания методов математического моделирования и системной динамики, визуализации математических понятий, развития системного стиля мышления и математической интуиции.