Информационное и математическое обеспечение моделирования процесса переноса загрязняющих веществ в атмосфере

Одним из важных аспектов в решении задач пограничного слоя атмосферы является постановка математически корректных и физически непротиворечивых начальных и краевых условий для системы уравнений гидротермодинамики. Постановка начальных и краевых условий во многом зависит от особенностей каждой конкретной обстановки. Поэтому рассмотрим некоторые общие замечания относительно условий при t=0 в моделях рассматриваемого типа задаются по данным измерений и таким образом относятся к числу входных параметров. Однако на практике получение детальной физической информации о начальных мезомасштабных полях затруднительно. Поэтому для проведения численных расчетов для данного типа атмосферной циркуляции начальное поле возмущений считаем нулевым. В этом случае решение задачи при небольших значениях времени будет описывать адаптацию метеорологических полей к условиям, когда в процесс включается турбулентность [1-4].

Объекты и методы исследований

Объектом исследования является изучение пограничного слоя атмосферы с начальными и краевыми условиями.

Методом исследования является система уравнения приземного слоя, куда входят скорость трения, масштаб потенциальной температуры и удельной влажности, высота приземного слоя, параметры поверхности для ветра и температуры, потока тепла, коэффициент трения и теплопередачи, температура и влажность подстилающей поверхности и некоторые непрерывные универсальные функции.

Учитывая, что информация о полях метеоэлементов поступает от сети станций, расположенных вне регулярной области или отсутствует, поэтому требуется предварительно провести процедуру восстановления значения метеоэлементов в углах регулярной сети. Для восстановления полей от данных измерений используем алгоритм описанный согласно работам Марчука Г.И., Пененко В.В., Протасова А.В [5,6,7]. В качестве краевых условий по горизонтали применяются равные нулю частные производные по соответствующим координатам от отклонения фоновых значений метеоэлементов на фиксированных точках.

Эти условия не противоречили данным о рельефе и температуре почвы, поэтому будем полагать, что функции о рельефе и температуре почвы, поэтому были такими, чтобы в некоторых малых окрестностях границы среды исчезали неоднородности рельефа и температуры подстилающей поверхности. По вертикальной координате краевых условий предполагаем, что на доступно большой высоте происходит затухание возмущений метеорологических элементов или ограничивается нижней границей инверий, которые соответствуют предположению, что движение ограничено сверху неподвижной плоскостью. Более реально, что если на некоторой незакрепленной поверхности вертикальная скорость является функцией от незакрепленной границы. На поверхности рельефа горизонтальные составляющие скорости равны нулю, а вертикальная составляющая равна полной производной от функции рельефа по времени. Температура и влажность задаются как известные функции. В этом случае функция, определяющая верхнюю границу, является одной из искомых характеристик. Поэтому использование такой модели требует преобразования системы уравнений гидротермодинамики, чтобы в ходе решения задачи, наряду с другими метеоэлементами определить функцию верхней границы и одновременно учитывать структуру рельефа подстилающей поверхности.

В настоящее время известны ряд способов определения высоты пограничного слоя атмосферы в зависимости от приземных турбулентных характеристик и параметров фонового значения, основанных на формуле Дир-дорфа, с величинами приземных потоков тепла и количества движения.

Основой для физического описания приземного слоя атмосферы является теория подобия для турбулентного режима в стратифицированной среде, указанной в работе Монина-Обухова [8]. В соответствии с этой теорией для приземного слоя атмосферы все статические характеристики пронормированные на масштабе характерной длины, скорости, температуры, являются универсальными функциями безразмерной высоты, которые обычно принимаются в качестве параметра гидростатической устойчивости. В этом случае, вертикальные предметы средних полей метеоэлементов с помощью некоторых функций, зависящих от безразмерных аргументов высоты. Знание конкретного вида этих функций позволяет определить турбулентные потоки тепла, влаги и движения. Используя теорию подобия Монина-Обухова [8] и эмпирические функции Бусинджера [9], запишем систему уравнений приземного слоя, куда входят скорость трения, масштаб потенциальной температуры и удельной влажности, высота приземного слоя, постоянная Кофма-на, параметры поверхности для ветра и температуры, потока тепла, коэффициент трения и теплопередачи, температура и влажность подстилающей поверхности и некоторые непрерывные универсальные функции. В дальнейшем, формулы для высоты приземного слоя будут использованы краевыми условиями для задач локальных атмосферных процессов в области выше приземного слоя, пока предположение, что температура и влажность подстилающей поверхности известной функции координат и времени выполняется. Для прогностических задач это предположение довольно грубо, поэтому для реальных случаев наряду с другими метеоэлементами определяются температура и влажность подстилающей поверхности, включая в систему уравнений замыкающих уравнений температуры и влажности подстилающей поверхности.

Результаты и их обсуждение

Рассмотрим совместные модели динамики пограничного слоя атмосферы во взаимодействии с термически и орографически неоднородной подстилающей поверхностью. Для суши это модель температурного режима почвы с уравнением баланса тепла на границе с атмосферой и модель влагообмена. Распределение температуры в почве описывается известным уравнением. В качестве условий на поверхности земли примем уравнение баланса тепла.

Как известно, температура приземного воздуха и суммарного испарения увлажненной поверхности зависят от инсоляции деятельности поверхности. Различия в инсоляции склонов в зависимости от их экспозиций, могут привести в условиях орографической неоднократности подстилающей поверхности к значительным мезометеорологическим контрастам. Поэтому для расчета потока солнечной радиации на поверхности склона используем ненормированную формулу из работы М.И.Будыка [10]. Во многих моделях динамики атмосферы для нахождения температуры почвы используются уравнения теп- лового баланса. Теплофизические характеристики почвы разнообразны, в результате чего даже на небольших расстояниях температуры над различными типами почвы резко различаются и тем самым влияют на динамику атмосферы в нижних слоях. Кроме того, тепловой и влажностный режимы в системе почва - воздух воздействуют на формирование и развитие растений из-за взаимной связи между собой и тем самым влияют на окружающую среду. Изменения влажности почвы влечет за собой изменение баланса радиации на поверхности земли из-за изменения альбедо подстилающей поверхности. С увеличением влажности альбедо уменьшается.

Решение системы уравнений гидродинамики при постоянном коэффициенте турбулентного обмена или турбулентной вязкости, показывает, что оно согласуется с некоторыми физически ясными свойствами интересующего нас течения, даже если толщину пограничного слоя рассматривать как заданный внешний параметр. Недостаток решения заключается в том, что из него следует пропорциональность сдвига ветра к сдвигу скорости геометрического ветра, при сколь угодно больших значениях коэффициента турбулентного обмена. Для замыкания системы уравнений пограничного слоя атмосферы относи тельно вертикальных коэффициентов диффузии применяем метод, основанный на решении уравнения баланса турбулентной энергии, операторы горизонтального турбулентного обмена рассчитывались через тензора вязких напряжений [4].

Необходимость использования различных подходов для описания вертикального и горизонтального турбулентного обмена связана с тем, что в уравнении баланса турбулентной энергии учитывается температурная стратификация атмосферы, что особенно важно для вертикального обмена. В природе при большой относительной влажности образуется облачность, в результате чего, в некоторых локальных областях, расположенных в верхних слоях атмосферы из-за выделения дополнительного притока тепла за счет конденсации изменяется стратификация атмосферы. Наблюдения над мезопроцессами, горизонтальные размеры которых несколько десятков километров, показывают, что они сопровождаются образованием облаков с горизонтальными размерами 5-10 км и вертикальными около 1,5-2,5 км. В связи с этим необходим учет фазовых переходов влаги.

Рассмотрим модели гидротермодинамики при следующих начальных и краевых условиях:

и ' = 0, v ‘ = 0, &  = 0 , q ' = 0, H ( x , y ) = H ⁰( x , y )   при t=0;

∂u ′      ∂v ′     ∂θ′

---= 0, --- = 0, --- = 0, --- = 0 при x = ± X ;

∂x     ∂x    ∂x

∂u′     ∂v ′      ∂θ′

---= 0, --- = 0, --- = 0, --- = 0 при y = ± Y ;

∂y    ∂y     ∂y

dt

где A T = Т теп - Т хол , H ⁰( x , У ) — начальная заданная высота слоя инверсии. Функции f, Q предполагаются заданными.

В данном случае имеем задачу о пограничном слое атмосферы при движении воздушной массы над термически и орографически неоднородной поверхностью со свободной верхней границей воздушной массы, которая учитывается в краевых условиях (4).

Преобразуем модели таким образом, чтобы получить уравнение для нахождения функции H ( x , у , t ).

С этой целью перейдем от переменных t , x , у , z к новым независимым переменным x* = x , y ‘ = y , t’ = t и определим вертикальную координату следующим образом [4, 12]:

д = z - S(x,y),                           где h (x, y, t t)

h ( x , y , t ) = H ( x , y , t ) - 5 (x , y ) .            (6)

Функция 5(x, у) описывает рельеф подстилающей поверхности. Ордината z теперь зависимая переменная, определяемая, согласно (6), как z (x, у5, t) — 5i (x, у, t) + 5( x, у). (7)

Переход от первоначальной системы координат t , x , y , z к новой t ' , x ' , у ' , 5 осуществляется с помощью следующих преобразований:

др  др  дер Э5   др  др  др Э5   Эф  Эф Э5          -

— =--1--- ,   — =--1--- ,   — =-- , ф — ( u , v , О , q , п ).  (8)

Э с   д с '   Э5д с'    Э у   Эу ’  Э5 ду ’    Э с   Э5 д с

В новых переменных символ индивидуальной производной будет иметь вид:

d p др    др ,. др - др

— — — + U — + V — + W— . (9)

dt дt     Эс ’ Эу ’д5

В (9) фигурирует неизвестная функция W(x , у, 5 , t ) (аналог вертикальной скорости),

-     д .ЭкOh

W — iw + 5 1--+ u --+ v — 1 + 5 u + 5 У .⁽¹⁰⁾

(дt    дс    д J xy

В новой системе координат модели гид- ротермодинамики, описывающие локальные атмосферные движения, примут следующий вид:

которая связана с W с соотношением:

ди' , Э л        дп ' дП , . .   ^дт_и   дг_п Э ,       ,        ,       .

+ U grad₈u —---- a j + lv +---11-- ( a_x r _n + a₂ t₁₂ + a₃ t_{x 3});

dt      ⁵            дx    Э5 ¹         дx     Эу    Э5 ^{1       z 1Z 3 13}

д с '    Э j       дп' дп'        , дт₂₁ дт₂₂ д

— + U grad ₈ v = — --- —a ^ ^- lu ' + —- + —- + —⁽ a т + a ₂ r ₁₂ + a ₃ ^T ₁₃);

д t               д у    Эй          д с     д у    Эй

^п = МО ;

Э5

Э

--+ U grad 5О + Shw + S5a, + u 55S S + О) + v 5 S + О ) = dt       5                         4        x      x,        yy,

Lw^ э     1  ЭН2   д ,

— —Ф + Q +---11-- ( a,T , + a₂T ? + a₃т ч) ;

Г                                    '  1  11       2  12       313' cp        дx   ду  да даЭ

— + ^U gr^ad 5 q ⁺ Y q ^hw + Y q & l 4 + ^{u (} Y q ⁵ x ^{+ Q} x ) ^{+ V (} Y q ⁵ у ^{+ Q} y ) = dt

Э21  Э22

= -Ф + "ЛП + IT + "ут.(.a1T11 + a2T12 + a3T13) ; дx   ду di   dhu'   div'   diw'„

— +---+---+ дt дс    ду

о        ,      др   др  _ др

Здесь grad р — u --+ v --+ i w — , ⁵      д с     д У     Э5

р — (u, v ,о ', q'), где 0x, Оу, Qx , Qy - горизонтальные градиенты фоновой потенциальной температуры и влажности.

• a, — Э°, a2 — Э°, a3 — h0 , a4 — 1° .(17)

• 1    Эс       Эу 3 дс

Начальные и краевые условия (1)-(5) преобразуются соответственно в следующие:

u' — 0, v' — 0, О — 0, q' — 0, Н(x,у) — Н0(x,у) при t=0;

д< — 0, 5^. — 0, ЭО — 0, ^L — 0 при дс

x — ± X ;

дс

ЭУ — 0 , ЭУ — 0 , ЭО — 0 , 0L — 0

Эу     ду     Эу     Эу при у — ±Y;(20)

u' — 0,  v' — 0, W — 0, О — q' — 0, п — 0 при 5 — 1.(21)

u — 0, v — 0, О' — / (x, у, t), q' — Q(x,у,t), tw — 0 при 5 — 0.(22)

Условие (22) имеет место в том случае, когда система уравнений пограничного слоя атмосферы решается без учета квазиодно-родного приземного слоя. С подключением уравнений приземного слоя вид краевых условий (22) несколько изменяется, что будет рассмотрено несколько позже.

Прежде чем перейти к решению задачи (1)-(2), целесообразно осуществить некоторое преобразование уравнений. Проинтегрируем уравнение неразрывности (16) по 5 . Учитывая условия для W при 5 =1, получим:

-h _ Г ( —tu '

S t | l S x

+

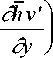
d 5 .

г

W ( ⁵ ) = - (1 — 5 - + J h          - t

—IU '   —IV 'Yre

----+----I d 5 - ^—    S y J

. (23)

При 5 =0 из краевого условия (22) и уравнения (23) следует:

В дальнейшем, наряду с уравнением (16), будем пользоваться уравнением неразрывности в форме (24). Подставляя (24) в (23), получим диагностическое уравнение для определения W ( 5 ) - аналога для вертикальной скорости:

W ( 5 ) = ¹ 5 [ ^f— h ^J    - x

—iv'

⁺ SS

d ^{5 —} J

f S hu ' I S x

+

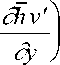
Модели, описывающие динамику пограничного слоя атмосферы, являются не-

K M

( j ~ A )²| Def\ ,

Ri >  1;

замкнутыми относительно величин _т. = _u._u , представляющих собой тензор вязких напряжений Рейнольдса. В настоящее время уже хорошо известно, что роль этих напряжений в динамике осредненного течения очень велика и пренебречь ими никак нельзя.

Суть моделей, основанных на замыка-

( K ~ A )²| Def | 1

где

—

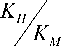
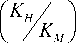
Ri , Ri <  1,

, (29)

~                   V.

A = ( A x * A y * A z y³    -

объем элементной расчетной ячейки сеточной области; K~ - числовая константа. Деформацию Def определим по формуле:

нии второго порядка состоит в том, что вторые моменты, а именно напряжения Рейнольдса и потоки скалярных субстанции не апроксимируются посредством приближения турбулентной диффузии, а сохраняются как неизвестные параметры. Для замыкания задачи вводятся уравнения вторых моментов. Моменты из третьего порядка, которые появля-

Def ² =¹ (d² +D² +D²\ + D² +D² +D² .(30)

Def    2 ( D 11 ⁺ D 22 ⁺ D 33 ) ⁺ D 12 ^{+ D} 13 ⁺ D 23 ^{V 7}

Число Ричардсона

следующем виде [15]:

Ri представим в

где

Ri =

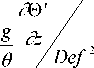
ются в уравнениях, апроксимируются на основании некоторых предположений подобия.

В данной работе следуя [13,14], симметричный тензор напряжения т,• , пред-

(I p 0 ©'| Def ²)

z

^S f©' dz

^S H

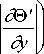
| ©'< 10 ^{— 3} e

| ©'| >  10 ^{— 3} o

ставим в виде функции, зависящей от тензора деформации D среднего движения следую- щим образом:

Т - - i, j

где D i, j

= ^D,.,, i, j=1, 2, 3,(26)

Su  -л,Su,

= — + — - 5 ij— . ⁽²⁷⁾

( Sx-j   S x     ’ Sx_k J

Поток тепла определим по формуле:

H = KH ^l, j =1, 2, 3,(28)

j H Sx где KM, KH - параметры кинематической вязкости и диффузии.

Для определения пространственно-временных изменений параметра K будем пользоваться формулировкой схемы замыкания:

дополнительное слагаемое а имеет стабилизирующий характер. Поскольку при наличии сильной орографической и термической неоднородности могут возникнуть большие температурные градиенты, введение параметра а способствует погашению мелкомасштабных колебательных процессов. В численных расчетах значения безразмерной константы К~ брались из [0,2-0,4]. При проведении численных расчетов в квазистатисти-ческом приближении применяется несколько упрощенное представление турбулентных слагаемых в виде:

∂ϕ

τ = µ ⁱ , τ = µ ⁱ , ,1 x ax ^{1,2 y} ay

H

∂ϕi

^T 13 = ^v     H I = M x —;

∂z

∂Θ ′

• 2    = МУ     , H3 = v ®

∂y

∂ q ′

∂ q ′

Qi=Mx d-, q 2=My dq-, qз = d

v q

∂ q ′ ∂ z ^,

i =1, 2,   ф = (u, v), где коэффициенты вертикального турбулентного обмена vu , ve , vq определяются из уравнения баланса энергии турбулентности. Такое упрощение имеет смысл, поскольку в нижних слоях атмосферы одним из существенных факторов, влияющих на турбулентную структуру пограничного слоя атмосферы, являются вертикальные градиенты скорости ветра и температуры, которые на 1-2 порядка превосходят горизонтальные градиенты.

В дальнейшем, поскольку горизонтальные размеры рассматриваемой области намного больше, чем вертикальные, ограничимся рассмотрением двухмерного тензора, а вертикальный коэффициент турбулентного обмена ν определим из решения уравнения баланса турбулентной энергии.

Заключение

В данном случае система уравнений пограничного слоя атмосферы с начальными и краевыми условиями решается с учетом члена образования жидкой фазы. И дополняется уравнением переноса и диффузии для удельной водности. Для численного моделирования гидрометеорологического режима промышленных районов необходимо иметь в качестве начальных данных значения метеоэлементов в узлах регулярной сетки. А измерения производятся на метеостанциях размещенных по территории крайне неравномерно. Поэтому возникает задача восстановления значений метеоэлементов на узлах сеточной области по их значениям на станциях. Вопрос о восстановлении структуры полей гидрометеоэлементов выполнен аналогично работы В.В.Пененко [11].