Информационное моделирование распыливания и испарения моторного топлива в дизельном двигателе

Введение. Вклад автотранспорта в загрязнение воздушной среды мегаполисов превышает 90 %. Кроме того, рост российского автопарка примерно на 60 % обусловлен его старением. Отсюда и потребность оценивать энергоэкологические характеристики двигателей внутреннего сгорания (ДВС) в зависимости от технического состояния, в частности состояния топливной системы, а также состава моторного топлива [1 – 3]. Реалистичное компьютерное моделирование выступает действенным инструментом, позволяющим совершенствовать существующие и создаваемые транспортные ДВС.

Постановка задачи и описание моделей. Способы формирования заряда в ДВС в значительной степени определяются агрегатным состоянием и другими физико-химическими свойствами топлива. Если в качестве энергоносителя используется каменный уголь, требуется произвести предварительную специальную обработку и подготовить топливо к сжиганию: измельчить его до пылеобразного состояния и смешать с жидким горючим или транспортной средой (водой) в эмульсию (суспензию). Двухфазную систему – однородную взвесь призмовидных твердых частиц углерода в жидкости [4] – впрыскивают в камеру сгорания (КС) через форсунки. Таким образом, технология сжигания в ДВС твердых угольных топлив представляет собой модификацию рабочего процесса с внутренним смесеобразованием.

При внешнем смесеобразовании в КС попадает сравнительно однородная по химическому и фазовому составу топливно-воздушная смесь, что позволяет квалифицировать динамику такого процесса как вырожденный случай внутреннего смесеобразования – с бесконечно быстрыми фазовыми переходами и гомогенизацией в начале такта сжатия. Поэтому, выбрав в качестве базовой модель внутрикамерного смесеобразования с твердыми частицами в составе топлива, мы предусматриваем все практически реализуемые ситуации.

Подача топлива в цилиндр осуществляется из трубопровода высокого давления Р_т , а ее динамика определяется изменением во времени проходного сечения 9 . Последнее служит параметром управления процессами в ДВС с внутренним смесеобразованием. Массовая скорость впрыска составляет [5]:

F ( t ) = 3 ( t ) [2( Р _т - Р )/ р ]^1/2 - (2 Р _т/ р )^1/2 Э ( t ),                                    (1)

где Р - давление рабочего тела в КС; р - плотность.

В элементах форсунки поток турбулизуется и, истекая в заполненную газом КС, дробится на капли вследствие тейлоровской неустойчивости [6, 7]. Распаду жидкой струи на капли препятствует энергия поверхностного натяжения Гельмгольца. Отношение мощности формовозмущающего и стабилизирующего факторов известно как число Вебера:

We = р и ² Л / п пов , (2)

где и - скорость капель; Л - диаметр капли; п _пов - коэффициент поверхностного натяжения.

Установившемуся дисперсному составу капель отвечает диапазон чисел We = 9-18, т. е. на диспергирование струи тратится 5–10 % взаимной кинетической энергии фаз [5, 6]. Возмущение жидкости в системе топливоподачи и турбулизация газа в КС направлены на улучшение качества распыла, т.е. на возможно более полное и мелкое дробление струи. Согласно [8], нагрев топлива сопровождается уменьшением коэффициента поверхностного натяжения, что также улучшает распыл:

п . = п . (1 - T / T кр )^11/9, (3) где T _кр - критическая температура; п ⁰ _пов - экстраполированное значение п _пов( Т ^ 0).

Критическое значение числа Вебера определяется в эксперименте с точностью до множителя ~ 2, что обусловлено полидисперсностью распыла. Шаблоном распределения капель по размерам выберем аналитически интегрируемый вариант обобщенной зависимости Розина–Раммлера [9]:

F p-p ( A ) = uV e\pi /\ i. (4) где а , в , у и 8 - экспериментально определяемые константы.

Подобрать три параметра модели (4) по экспериментальным данным, объем и точность которых ограничены, проблематично. Требование аналитической интегрируемости (4) позволяет связывать в и 8 соотношением в = 8 - 1 . Неопределенность критического числа Вебера составляет ~ 2^1/2 [5, 6]. Распределение (4) имеет также подходящую ширину по уровню 0,1 . max{ F _Р-Р( Л )} при 8 ~ 3. Наконец, распределение (4) с 8 = 3 почти симметрично относительно максимально вероятного значения и близко к нормальному.

Предложенная модель дробления струи позволяет связать показатель диспергирования F _p._p (A) с единственным управляющим параметром:

Y = Y () = 2/3 [ р и ²( п .,, WeJT « 3^.10^-4 [ р и Хов ]³, (5) который следует трактовать как обратный характерный размер структурно устойчивых частиц жидкой фазы.

Из уравнений (1) и (2) следует, что начало и конец впрыска характеризуются наихудшим измельчением струи. Практически крупные капли раннего формирования успевают испариться и сгореть, а финальная порция плохо распыленной жидкости оказывается в невыгодных условиях. Отмеченное обстоятельство определяет неполноту сгорания и оправдывает полезность следующей оценки. Для модели монодисперсного распыла мгновенный диаметр капель

Л ( t ) ~ и ^-2 ~ Э ( t )^-2. (6)

Когда пропускное сечение открывается мгновенно в момент t _впр

Э(t) ~ sign(t -tвпр), (7) проблем не возникает: все капли идентичны. В противном случае часть струи измельчается недостаточно. Долю неудовлетворительного распыла можно определить, приблизив начальный и конечный участки функций F(t) и Э(t) степенной функцией вида tа: при несимметричной динамике впрыска параметр а, конечно, отличен для этих участков. Диаметр структурно устойчивых жидких частиц, образующихся впоследствии из порции потока, впрыснутого в промежутке времени t - (t + dt), Л(t) пропорционален t "2“, а их общая масса - Э(t)dt. Обозначив максимально допусти- мый диаметр капли Лкр, путем несложных преобразований получим зависимость массовой доли недораспыленного топлива:

L = ( Л кр / Л _т1П) ^{-( а +}1)^{/2 а} ,                                           (8)

где Л _т1п - диаметр капель в момент максимально интенсивного впрыска t _max. При выводе (8) предполагалось, что впрыск с различной динамикой (значениями а ) характеризуется одинаковыми продолжительностью t _max и суммарной дозой (массой) жидкого топлива, причем Л _кр >  Л _т1п. Техническая подоплека этих ограничений очевидна: а) для эффективного смесеобразования требуется осуществлять его в течение ограниченного периода; б) если чрезмерно крупными оказываются даже капли, отвечающие наилучшим условиям дробления, повышение качества распыла требует наращивания энергетики впрыска.

Интеграция моделей впрыска и неоднородного диспергирования сопровождается появлением «перекрестных членов», отвечающих мультипликации «слабых мест» обоих процессов. Поэтому динамику впрыска следует оптимизировать очень аккуратно.

Распыливание топлива в КС сопровождается постепенным сопряжением траекторий отдельных капель с траекториями мезообъемов газов. После измельчения дроблением ведущая роль отводится процессам испарения жидких частиц и газофазной гомогенизации и/или выгорания отдельных капель.

Бесполезность наиболее общей модели испарения жидкого топлива для наших целей становится очевидной, если учесть следующие обстоятельства [4, 10, 11]:

• –    испарение может происходить в до- и закритическом режимах;

• –    многокомпонентные топлива могут испаряться как с «разгонкой» фракций, так и без нее;

• –    испарение может сопровождаться крекингом топлива или происходить без реакций;

• –    фронт горения может примыкать к поверхности испарения или отсутствовать в диффузионной окрестности;

• –    возможны ламинарный и турбулентный режимы обтекания жидких частиц;

• –    в состав жидкого топлива могут входить мелкодисперсные частицы твердых горючих веществ, например угольная пыль;

• –    эмульсионные топлива часто содержат воду, критическое давление которой на порядок выше, чем Р _кр используемых углеводородных топлив и выше достижимого давления в КС.

Корректно учесть перечисленные обстоятельства не представляется возможным, поэтому динамику фазовых превращений будем описывать с опорой на особенности испарения жидкого топлива в типичном ДВС, работающем по циклу Дизеля [10, 11].

Б. Срезневским экспериментально установлено, что диаметр испаряющейся сферической капли Л уменьшается по закону:

dЛ/dt = - D т Л-1, где Dт - коэффициент диффузии паров топлива в вакуум.

Коэффициент диффузии зависит от молекулярного веса топлива ц т , температуры и давления газа в КС:

D т = 5 10 5ц,-1/2 T 7/4/Р, если давление измерять в атмосферах, а Dт - [см2/с].

Динамика газификации топлива, поступающего в КС с массовой скоростью G ( t ), задается уравнением:

dfdt - Dт /2Л df дЛ = F(Л, t), которое связывает темп фазового перехода с дисперсностью жидкости (ее определяет функция распределения капель по размерам f=fЛ, t), мкм-1) и законом топливоподачи F(Л, t), мкм-1-с-1.

Для наших целей представляет интерес связь между массой испаренного на некоторый момент топлива m ( t ) и динамикой его впрыска G ( t ). Последовательное рассмотрение вопроса включает два этапа: первый - решение уравнения (11) для конкретного источника F(Л, t ); второй -вычисление мгновенной скорости накопления жидкого топлива в КС и темпа газификации капель на основе f Л , t ).

Семейство характеристик (11) задается уравнением:

d Л / dt = - D т / Л или Л ² = Л о ² - D _т t ,                         (12)

где Л _о отвечает начальному размеру капли. Действие источника F ( Л , t ) сводится к «загрузке» каплями соответствующих характеристических линий. Сингулярность ~ 1/ Л в коэффициенте уравнения (11) при df/дЛ побуждает прибегнуть к замене независимой переменной Л ^ m = рЛ ³ и оперировать уравнением:

df/dt - 3/2 Dт m1/3 df/dm = M(m, t).

Соответственно изменятся функция распределения капель по размерам

FP-P(K) = 3уЛ2 ехр(-уЛ3)  ^    МР—Р(m) = у/р exp( у рm)

и уравнение характеристик (ниже константа D _т увеличена в 6 раз):

Л2 = Ло2 - Dт t ^     m2/3 = mо2/3 - Dт р2/3t.

Нормированная на единицу величина М _Р-Р( m ) во втором из уравнений (14) легко модифицируется для учета временного фактора.

Учитывая, что согласно (4)-(6) показатель измельчения струи у ~ G ( t )⁶ , получаем явный вид источникового члена в уравнении (13):

M(m, t) = (^/р)2G(t)13 exp( х р G(t)6 m), где £ - коэффициент, характеризующий распыливающее устройство.

Нетрудно убедиться, проинтегрировав (16) последовательно по обеим переменным, что to

J m M(m, t) dm = G(t)   и J G(t) dt = GE.

оо

В интегралах (17) нормирование осуществлено по цикловой подаче – массе впрыскиваемого за рабочий цикл топлива G _Е .

При выбранных модельных распределениях средняя масса капель < m ( t )>, поступающих в КС в момент времени t :

• < m ( t )> = р / у = р /^ G ( t )⁶],                                     (18)

что будет использовано при упрощении модели впрыска–распыливания.

Уравнения (11) и (13) позволяют физически корректно учесть динамику испарения капель неодинакового размера, поступающих в КС в различные моменты времени. Общее решение (13) получается интегрированием функции источника М _Р-Р( m , t ) вдоль характеристик (15) и имеет вид: t

Яm , t ) = J M р-р ([ m^2/3 + D т р ^2/3( t - т )]^3/2, т ) d т .                           (19)

о

На основании массово-геометрических характеристик жидкой фазы в КС (19) можно опре-t делять массу испаренного топлива как разность масс впрыснутой JG(T)dт и еще не испаренной to

J f(m, t) dm жидкости. Рассчитываемая таким способом массовая скорость газификации, состав-о ляет:

to

Г ( t ) = J m [ df ( m , t)//dt ] dm .                                    (20)

о

Упростить модель позволяют следующие соображения. Правую часть (20) можно записать в виде:

to J о

m [ df ( m , t )/ dt ] dm = d / dt

to J о

m f ( m , t ) dm = d / dt {< m ( t )> J f ( m , t ) dm }. о

Если дополнительно предположить, что характерное время испарения отдельных капель меньше, чем временной масштаб изменения их числа, можно представить правую часть (21) как to

to

дIdt {< m ( t )> J f(m , t ) dm } ~ д < m ( t )>/ dt ' J f ( m , t ) dm .

Оценить первый множитель в (22) можно при помощи уравнения характеристик (15): д < m ( t )>/ dt = 3/2 . D _т р ^2/3< m ( t )>^1/3. Второй, представляющий собой число капель в КС, очевидно, равен M ( t )/< m ( t)>, где M ( t ) - масса жидкой фазы.

С учетом выполненных замен и подстановок (20) трансформируется в уравнение:

Г ( t ) = 3/2D т ( р /< m ( t )>)^2/3 M ( t ), (23) а динамика суммарной массы жидкой фазы в КС определяется уравнением (23) и условием материальной консервативности:

• d M / dt = G ( t ) - 3/2D т (р/< m ( t )T 3 M . (24)

Подобная модель с постоянной величиной < m ( t )> = < m > использована в работе [12]: полидисперсность распыла учитывалась качественно – заменой «сингулярного» уравнения испарения, отвечающего конечному времени существования капли, «размытым», согласно которому капли существуют вечно.

Далее следует задать правдоподобный закон эволюции параметра (/р)2/3, отвечающего площади поверхности среднестатистической капли в КС: необходимо учесть влияние на нее как собственно испарения, так и влияние источника. Нетрудно убедиться, что уравнение d2/3] [(£ G(t)7/р)/(M(t)/)], (25) в котором размер вновь поступающих капель определяется законом впрыска G(t) и соотношением (18), удовлетворяет предъявленным требованиям.

Система обыкновенных дифференциальных уравнений (ОДУ) (24)–(25) представляет собой упрощенную модель испарения топлива в дизелях. Для ее получения использовался метод осреднения уравнения с частными производными (УЧП), состоящий в понижении пространственной размерности путем введения «эквивалентной» нелинейности.

Ценой отказа от использования в модели испарения УЧП (13) служат жесткость и нелинейность результирующих ОДУ (24)–(25), заметно усложняющие их численное интегрирование. Кроме того, в момент начала впрыска и/или при чрезвычайно интенсивном испарении M « 0 динамика средней площади капли не подчиняется (25) и необходимо пользоваться уравнением (18).

Согласно (24), в динамике жидкой фазы выделяются переходный и квазистационарный этапы: в начале подачи топлива M ( t ) ~ J G ( t ) dt ; в установившемся режиме M ( t ), подстраиваясь под темп впрыска, принимает значение около 2/3^.[ D _т р 2 ^/3^ ^2/3-G ( t )³]; по окончании поступления капель в КС величина M стремится к нулю с характерным временем D _т^-1(< m ( t )>/ р )^2/3. С другой стороны, такое поведение обеспечивается свойствами уравнения (13), характеристики которого разбивают мировую плоскость { m х t } на области влияния источника и начальных данных. Переходные режимы в динамике жидкой массы, определяемой ОДУ (24)–(25), обусловлены пространственно-временной ограниченностью источника капель.

Функцию впрыска G ( t ) удобно задать линейной комбинацией S Gi ( t ) звеньев вида:

Gi(t ) = Ai ( а + 1) ( t - 1 0 ) ^a i / A t“^{i +1} exp[-( t - t ⁰ i )/ A ti ) ^a i ⁺¹] sign( t - t°), (26) где Ai - удельный вес; a i , t ⁰ i и A ti - форм-факторы i -го звена.

Сумма нормируется очевидным образом: S Ai = G _S . Практически для аппроксимации реальных законов топливоподачи достаточно двух слагаемых типа (26). Удобно положить a. 1 « 1/3, a ₂ » 3, 1 01 ~ 1 ⁰ ₂ и A 1 1 ~ A 1 1 , а A 1 / A ₂ выбрать в пределах 3-5. Если имеются данные о реальной динамике впрыска, целесообразно параметры модельного распределения (26) определить как параметры аппроксимации.

Результаты компьютерного эксперимента. Для сопоставления различных способов описания кинетики газификации жидкого топлива в дизелях приведем результаты соответствующих тестовых расчетов. Объектом моделирования выбран цилиндр тепловозного дизеля: его рабочий объем составляет (15 – 20) ⋅ 10³ см³, частота вращения коленвала – 10 – 15 с^–1, цикловая подача топлива G Σ ~ 1 г, Δ t ~ 4 мс, характерный начальный диаметр капель топлива – 50 мкм, коэффициент диффузии D т ~ 10^–2 см²/с.

Отвечающая выбранным параметрам динамика впрыска и распыливания капель представлена на рис. 1.

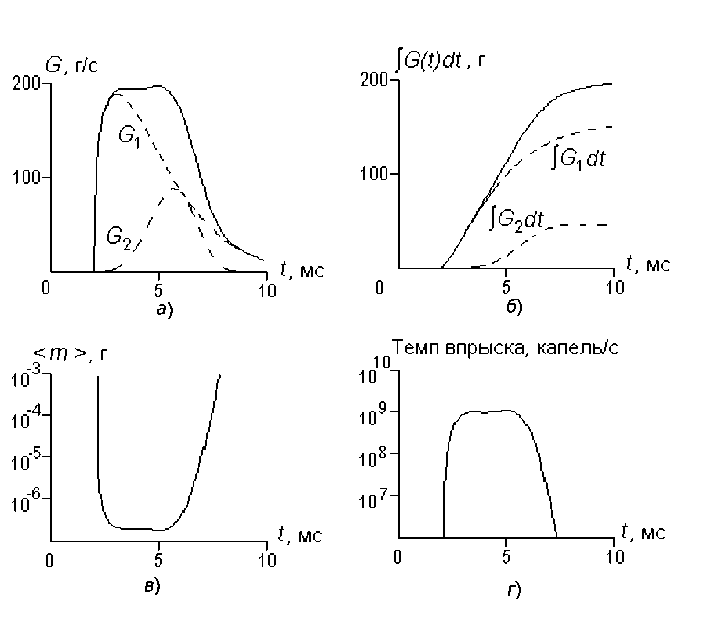
Рис. 1. Количественные характеристики впрыска топлива в тепловозном дизеле:

а – массовая мгновенная подача жидкости; б – массовая интегральная подача жидкости; в – средняя масса капель; г – секундное число капель; G ₁ = 0,77 г и G ₂ = 0,23 г – массовые доли топлива, относимые соответственно к слагаемым формулы (26)

Данные рис. 1 свидетельствуют, что качество смесеобразования определяется продолжительностью и переходными режимами топливоподачи.

Теперь сопоставим описанные модели распыливания–испарения различной детальности с тем, чтобы выбрать адекватную для интеграции в новую версию автоматизированной системы МОТОР [13, 14].

Наиболее подробно процесс газификации топлива описывается уравнением (13). Его решением (19) для выбранных нами условий, служат массово-временное распределение частиц в источнике, камере сгорания, а также момент m f ( m , t ), изображенные на рис. 2. Условия расчетов соответствуют тепловозному дизелю на режиме номинальной мощности.

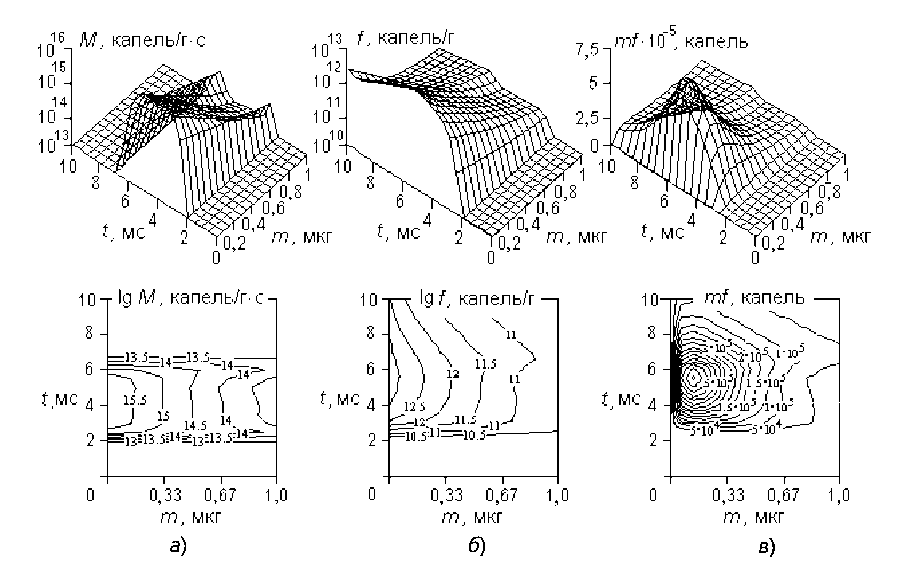
Рис. 2. Статистические характеристики распыленного топлива в дизеле согласно модели (13), (16): а – масса жидкого топлива в камере сгорания; б – распределение капель по размеру;

в – «массовая представительность» капель размера m

Результаты компьютерного эксперимента, показанные на рис. 3 и 4, призваны прояснить зависимость динамики испарения топлива от качества распыла, задаваемого величиной ^ , и коэффициента диффузии топлива D _т. На рис. 3 видна геометрия зон влияния этих параметров на конечный результат. В частности, отражены: 1) усиление зависимости f(m, t ) от D _т на завершающей стадии процесса (рис. 3, а ); 2) устойчивость формы распределения капель по размерам при разумном варьировании показателя диспергирования £ ; 3) область сильного влияния одновременно обоих параметров (характеризуется высокими значениями и сгущением изолиний) совпадает с завершающей фазой впрыска.

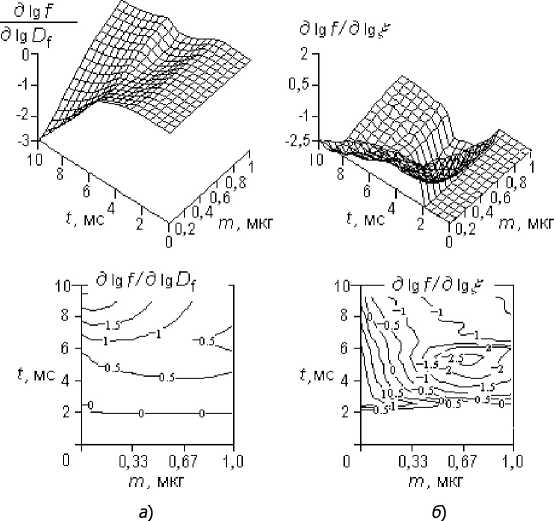
Рис. 3. Влияние коэффициентов D т ( а ) и ^ ( б ) на распределение капель по размерам согласно модели (13) в условиях рис. 1 и 2

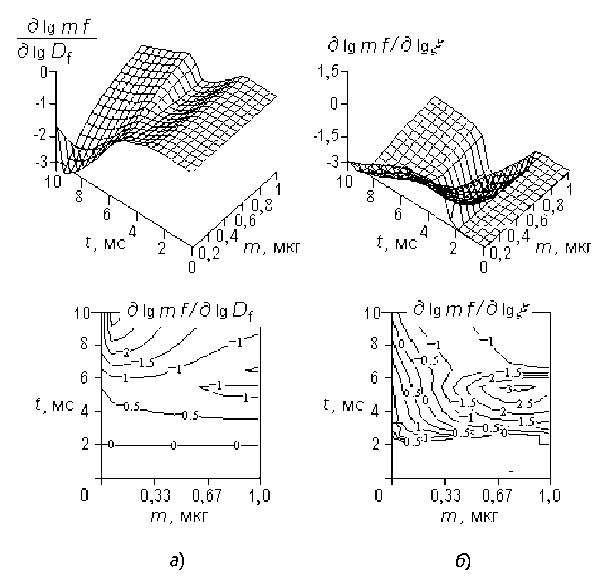
Рис. 4. Влияние коэффициентов D _т (а) и ^ (б) на динамику «массовой представительности» капель согласно модели (13) в условиях рис. 1 и 2

Для ответа на вопрос, насколько правомочным является упрощенное описание впрыска при помощи ОДУ (23)–(25) и их предельных форм, необходимо выполнить специальные сопоставительные расчеты. В качестве сопоставляемых моделей выберем следующие три: 1) основанную на УЧП (13); 2) использующую аппроксимирующие ОДУ (23)–(25); 3) совпадающую с предыдущей, но предполагающую постоянство средней массы капель, и в результате определяемую единственным уравнением (24).

Естественными объектами такого сопоставления (его результаты представлены на рис. 5 и 6) являются усредненные по мгновенному массовому распределению f(m , t ) величины < m ( t )>^2/3 и M ( t ). На рис. 5 показаны средняя поверхность испаряющихся капель (рис. 5, а ) и масса жидкого топлива (рис. 5, б ) в КС тепловозного дизеля, рассчитанные в рамках различных моделей испарения: сплошные линии без маркеров – модель, основанная на УЧП (13): заштрихованный на фрагменте рис. 5,а коридор соответствует интервалу < m ^2/3/ р > - < m / р >^2/3.

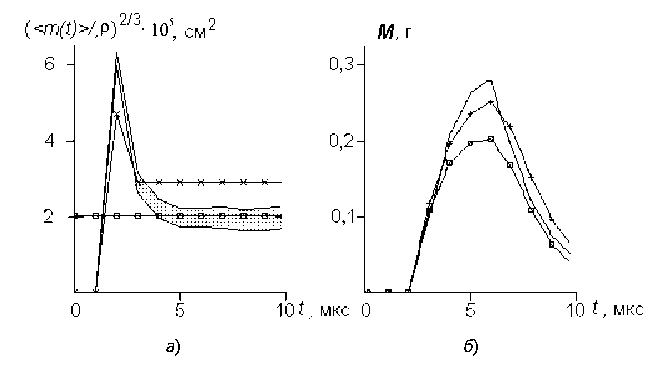
Рис. 5. Характеристики распыливания–испарения согласно (13), (24)–(25), (24):

а - средняя поверхность капель <  m ( t )>^2/3 ; б - количество жидкого топлива в камере сгорания; х - описание при помощи системы ОДУ (24)-(25); □ - модель, использующая одно ОДУ (24)

Представленные на рис. 5 данные подтверждают квазистационарность среднего размера капель в КС, чем оправдывают использование предложенных здесь упрощенных моделей испарения. Погрешность упрощенных моделей газификации топлива (24) и (24)–(25) в редких случаях превышает 20 – 30 %, что позволяет использовать в интегрированной модели рабочего процесса ДВС математическое описание испарения, основанное на предположении о постоянстве среднего размера капли и выражаемое единственным ОДУ (24).

Существенно, что сопоставляемые модели, несмотря на различную степень детальности, сходным образом воспроизводят зависимость доли испаренного (за отведенное время) топлива от качества распыливания ξ и легкости испарения D т . Расчеты показывают, что неполнота испарения, а следовательно, и сгорания сильно зависят как от качества распыливания ( д ln М ост / д ln ξ → –1), так и от транспортных свойств рабочего тела ( д ln М ост / д ln D т → 2).

Выводы. Совпадение динамики испарения в предложенной иерархии моделей различной подробности заметно облегчает моделирование внутрицилиндровых процессов, в том числе образования токсичных веществ. Результаты работы служат также строгим научным обоснованием упрощенного описания испарения посредством модели (24), применявшегося авторами в предшествующих исследованиях. На основании предложенных моделей выявлены критичные условия и режимы в системе процессов впрыска, распыливания и испарения топлива в дизелях.