Информационное обеспечение поддержки принятия решения получения банковской гарантии

Банковская гарантия (БГ) является распространенной формой обеспечения условий участия в конкурсах в соответствии с законами № 44-ФЗ «О контрактной системе» и № 223-ФЗ «О закупках госкомпаний» и последующего исполнения обязательств перед заказчиками, в которых банк (или другая организация) берет на себя финансовую ответственность за ненадлежащее исполнение поставщиком условий государственного контракта.

Сегодня сектор обеспечительных мер на рынке госзаказа и банковский продукт (БП), именуемый банковская гарантия (БГ), является успешной точкой роста банковского сектора. Становятся популярны межбанковские интернет-площадки по выдаче БГ, которые работают с достаточно большим объемом заявок на получение БГ и большим числом банков, предоставляющих такой продукт. Именно поэтому оптимизация процесса распределения заявок на получение БГ является сегодня актуальной.

Процесс выдачи банковской гарантии по своей сути аналогичен процедуре выдачи кредита. Обычно банковские системы предлагают своим клиентам рассмотрение заявки в ускоренном режиме [1], а также упрощенное оформление документов по банковской гарантии [2]. Это реализу- ется посредством подключения к базе данных официального сайта госзакупок РФ и использования электронного документооборота. Подключение к базе данных позволяет мгновенно получать необходимую информацию о любом тендере, поставщике, заказчике, требованиях обеспечения контракта. Юридическая значимость электронного документооборота подтверждается сертификатом электронной цифровой подписи. Доступ к функциональным возможностям системы предоставляется через Личный кабинет, в котором предусмотрен набор полезных инструментов для удобной и эффективной работы. Уровень автоматизации процесса выдачи банковской гарантии зависит от информационной насыщенности поддержки комплексного решения, организуемой в виде интеграции с внешними сервисами и внутренними источниками данных организации, а также наделения системы алгоритмами принятия решения [3] на основе методологии банка или интеграции с аналитической системой. Обязательной составной частью решений является электронное клиентское досье, описание входных и выходных параметров, функций веб-сервиса, входящих в состав автоматизированной банковской системы (АБС).

Процесс обработки и выдачи заявки на получение банковской гарантии можно условно разделить на три обобщенные стадии: Заведение Заявки, Рассмотрение Заявки и Выдача Продукта (БГ).

При подаче Клиентом заявки на БГ Клиент сам выбирает Банк (IBank), заполняет свой профиль в инстанции выбранного Банка. Продолжение бизнес-процесса дистанционной выдачи банковской гарантии уже происходит в личном кабинете IBank с возможностью входа и отслеживания статуса заявки в разделе «Рассчитать банковскую гарантию», вкладка «Мои заявки». Существенным недостатком являются высокие требования банков к Клиентам в вопросе подтверждения финансовой благонадежности. Банки применяют разные методики оценки финансового положения и кредитоспособности Клиентов, в анкете-заявке клиента на получение гарантии около 60 параметров, что значительно увеличивает время на обработку заявки.

Процесс	Время
Рассмотрение заявки с проверкой финансовых показателей вручную	24 ч
Заведение Заявки. Ввод данных Клиентом, заполнение профиля	10–30 мин
Выдача БГ	2–3 с
Рассмотрение заявки без проверки финансовых Показателей (статус предварительно одобрено)	При пиковой нагрузке время обработки одной поданной заявки составляет не более 15 мин, а в среднем не превышает 5 мин

График зависимости времени обработки заявки от суммы БГ1 представлен на рис. 1.

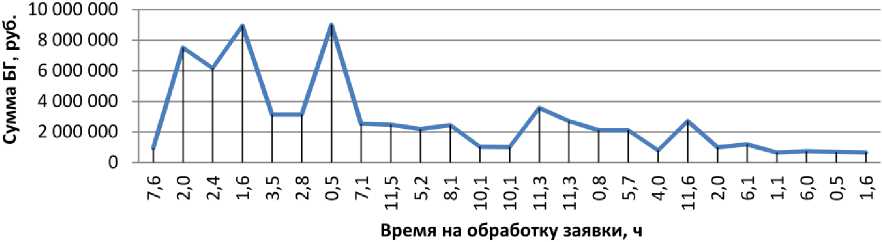
Рис. 1. График зависимости времени обработки заявки от суммы БГ на электронной бирже

Клиент подает заявку, заполняет анкету, ее обрабатывают одновременно по нескольким банковским инстанциям, т. е. над одной заявкой работают несколько менеджеров разных

• ¹    Данные взяты с сайта: My-Bg.ru. Электронная биржа банковских гарантий. – https://my-bg.ru/about/ (дата обращения: 30.04.18).

Управление в социально-экономических системах

банков. На исполнение заявку на получение БГ получает только один банк. В этом случае увеличивается время работы на инстанции банка без гарантии получить заявку. Обычно клиенты сами выбирают инстанцию банка, в этом случае время обработки заявки не увеличивается, но увеличивается риск неполучения банковской гарантии (БГ) и время на подбор следующего банка. На каждой банковской инстанции андеррáйтинг производится по своей скоринговой модели. Схема обработки заявки по нескольким банковским инстанциям представлена на рис. 2.

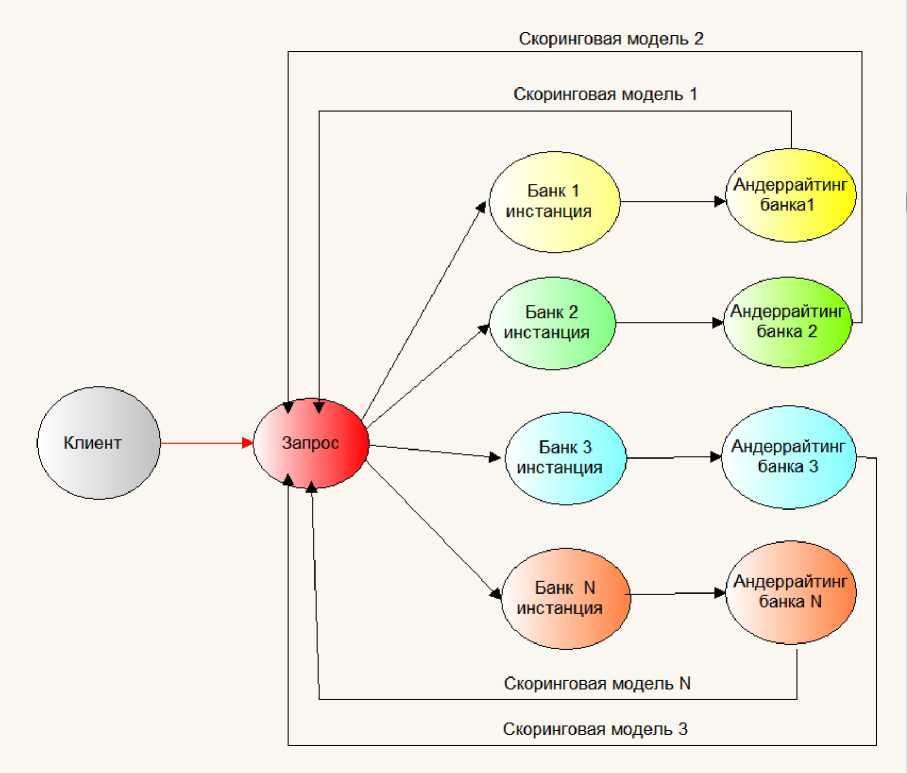
Рис. 2. Схема обработки заявки по нескольким инстанциям

Для сокращения времени обработки заявки и оптимизации процесса распределения заявок на банковские продукты необходимо формализовать процесс по единому унифицированному профилю для всех банковских инстанций [4]. Для этого определены единые критерии для заявки и параметры банков. В этом случае в едином окне подачи заявки производится автоматический выбор оптимальной скоринговой модели и по ней производится андеррáйтинг. Схема обработки заявки на одной инстанции в едином окне андеррáйтинга представлена на рис. 3.

Основная цель разрабатываемого алгоритма состоит в автоматизации процесса распределения потока заявок в режиме реального времени с учетом имеющихся предпочтений и ограничений. При этом критерием оптимальности является время распределения и количество заявок, распределенных по банкам, выдающим БГ за один пул.

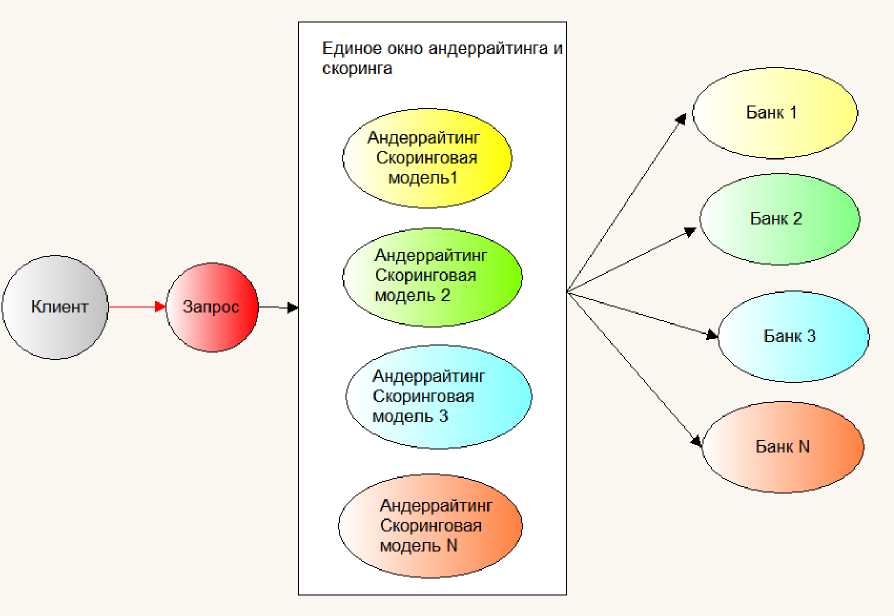
Рис. 3. Схема обработки заявки на одной инстанции

Постановка задачи

Первоначально определяются группы параметров, определяющих порядок очерёдности заявки от компании-заявителя (Принципале) и группа параметров, определяющая коэффициент приоритетности банка (Гарант), выдающего БГ. Необходимо распределить поступающие заявки на БГ среди банков гарантов.

Подобного рода задачи хорошо решаются методами, описанными в работах [5–7], достаточно изучены и реализованы как в виде алгоритмов, так и в виде программ. Например, в работе [8] аналогичная задача распределения заказов таксопарка решена путем оптимизации венгерского метода. В работе [9] оптимизация распределения кредитных заявок на примере ПАО Сбербанк решена исходя из того, что минимальное время исполнения каждой заявки в потоке обеспечивает минимальное время исполнения всего потока заявок. Несмотря на множество решений [10–12], из-за нестандартности математической модели, добавления критериев, роста требований к результатам необходима адаптация и оптимизация существующих решений под конкретные области применения.

На основании анализа информации о банке (Гарант) и заявки на БГ от компании-заявителя (Принципале) определяются параметры оценки приоритетности заявки компании-заявителя и банка, выдающего БГ. Необходимо распределить пул (пул – одновременный поток заявок за единицу времени) поступающих заявок на получение БГ среди банков-гарантов таким образом, чтобы число нераспределенных по банкам заявок было минимально возможным с учетом условий выдачи БГ конкретным банком.

Для упрощения задачи принимаем, что заявки в пуле являются однородными, распределение заявок зависит от критериев, определяемых банками. Критерии определяют поступления заявки именно в тот банк, которой более других имеет реальную возможность выдать БГ.

Решение задачи

Необходимо выбрать оптимальное распределение заявок по банкам. Существует N = ∑ X n заявок ( n номер заявки i = 1, n ), в одном пуле имеется a i единиц заявок и m банков (номер банка j = 1, m ), которые могут реализовать в зависимости от допустимого объема БП для каждого банка

Управление в социально-экономических системах

b j единиц заявок соответственно. Известны коэффициенты приоритета выбора банка, которые будем обозначать: c ij – коэффициент приоритета выбора i -й заявки к j -му банку; х ij – заявка, отправленная j -му банку. Необходимо распределить все входящие заявки по банкам, которые могут реализовать данный вид БП, в нашем случае банковскую гарантию (БГ), за минимальное время и с максимальной эффективностью.

Цель решения задачи – минимизация суммарных коэффициентов, для чего находится значение целевой функции:

c 11

F = C i

c m 1

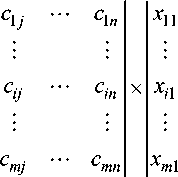
x 1 j

x 1 n

x ij

xin

^ min;

x mj

x mn

nm

^F = ZE c ij x ij ^ min.

i = 1 j = 1

Для вычисления функции F необходимо предварительно рассчитать коэффициенты c ij и определить x ij .

Предположим, что в систему поступает N заявок и отправлено в определенный банк на рассмотрение N p заявок. Необходимо минимизировать количество входящих заявок, не отправленных по банкам и находящихся в статусе ожидания:

△ N_m in = N - N_p = E ”=i a_t - E^ i b j .

Рассмотрим процесс распределения заявок при условии, что все заявки должны полностью распределяться между банками, следовательно, можно составить равенство

E T=ia_i = E T=ibj .                                                                           (2)

Так как рассматриваются заявки, распределенные за время обработки одного пула, необходимо учитывать время, затраченное на обработку заявки х ij . Следовательно, можно представить множество заявок x ij за один пул в виде

X ij ^t i E^X i +t j E 7=i X i ,                                                                  (3)

где t i – время распределения i -й заявки по j -му банку, t j – время принятия i -й заявки j -м банком.

Ограничения задачи:

Х-1-И                        •        -----

E ILi ^ ij = a, i = 1,n ;

^E yLi % ij = b, j = m ;                                                                     (5)

Хц > 0, i = 1, n, j = 1, m .                                                                       (6)

Первое условие (4) предполагает, что заявки должны быть распределены полностью, второе условие (5) – что объем заявок по каждому банку должен быть удовлетворён, третье условие (6) – что объем входящих заявок должен быть неотрицательным. Системе ограничений задачи могут соответствовать несколько допустимых планов распределения заявок.

Рассмотрим возможные случаи плана распределения заявок по банкам.

• 1.    Пусть объем входящих заявок превышает возможности банков, т. е. имеет место следующее неравенство

• 2.    Если объем возможностей банков на обработку и получение заявок на БГ превышает объ-

• ем входящих заявок в одном пуле, тогда имеет место неравенство

t i E> i >t j E T=i b j .                                                                        (7)

В этом случае для обеспечения условий решения задачи вводится условная единица заявки, обеспеченная банком (bn + 1) с коэффициентом приоритета выбора cn=i,j = 0, j = 1,m b„+i = E2i=i -ElLibj-

После введения получаем равенство (2).

• t^a i j .

В этом случае для обеспечения условий получения заявки вводим условную заявку в одном пуле ( a n + 1) с коэффициентом, определяемым по формуле

Ст=1д = 0, i = 1,n при

• a_n+ i = S m=i b ; -^« i .

После этого условие задачи сводится к первому варианту (7).

Далее задачу можно решить известным методом потенциалов.

По условию все заявки должны быть распределены по банкам, следовательно,

I^ i C j = 1

при условии с„min < e, (cn - Zj) > e, где Zj – относительная величина, равная количеству заявок в j-м банке Sj, отнесенному к общему количеству заявок S:

• 2 = ^^

Zi    s, в идеале Zj должно стремиться к значению сij.

Определение коэффициента приоритета банка Cij

На основании анализа информации о Банке и заявки от клиента определяется множество коэффициентов приоритета распределения заявки по банкам с_i j . На основании экспертных данных формируются критерии, определяющие коэффициент с ij . Коэффициент приоритета определяет область наиболее точного соответствия банка и заявке на получение БГ. Определим критерии, регламентирующие применение коэффициентов приоритета по заявке. Эти критерии можно разделить на 2 группы.

Первую группу составляют параметры банка (α i ), определяющие перечень условий, по которым заявка должна быть получена именно данным банком. Как правило, это параметры с фиксированными значениями (выбор из ограниченного множества конкретных параметров).

Вторую группу составляют параметры, по которым можно оценить уровень соответствия заявки коэффициенту приоритета банка ( q i ) . Необходимо придать каждому параметру второй группы свой вес, который для параметров первой группы имел смысл блокирующего коэффициента, а в данном случае является весовым коэффициентом, определяющим значимость параметра для коэффициента приоритета решения.

При анализе банковских продуктов были выявлены основные критерии, влияющие на степень оценки кредитного суждения и рисков по выдаче БГ.

Значения параметров банка (Гарант) α i

(α 1 ) Сумма обеспечения БГ

Сумма обеспечения БГ	Вес α 1
До 1 млн	0,25
1–10 млн	0,4
10–50 млн	0,2
50–100 млн	0,15

(α 2 ) Количество стоп-информации (факторы)

Количество стоп-информации (факторы)	Вес α 2
10	0,4
20	0,35
30	0,25

Управление в социально-экономических системах

(α 3 ) Срок выдачи БГ

Срок выдачи БГ	Вес α 3
1–2 дня	0,4
2–3 дня	0,35
3–5 дней	0,25

Значения коэффициентов компании-заявителя (Принципале) q i

( q 1 ) Сумма БГ

Сумма БГ ( P 1 )	Вес q 1
До 1млн руб.	0,15
1–1,5 млн руб.	0,3
7–10 млн руб.	0,25
10–50 млн руб.	0,2

( q 2 ) Количество Госконтрактов за последние 3 (три) года вне зависимости от статуса Госконтракта

Количество Госконтрактов за последние 3 (три) года вне зависимости от статуса Госконтракта ( P 2 )	Вес q 2
5 и более	0,25
2–4	0,3
1	0,15
0	0,2

( q 3 ) Стоимость чистых активов

Стоимость чистых активов ( P 3 )	Вес q 3
Чистые активы > уставного капитала	0,7
Чистые активы ≤ уставного капитал	0,3

( q 4 ) Возраст компании

Возраст компании ( P 4 )	Вес q 4
От 4 месяцев	0,15
От 6 месяцев	0,25
От 12 месяцев	0,3

( q 5 ) Срок БГ

Срок выдачи БГ ( P 5 )	Вес q 5
До 30 дней	0,15
До 6 месяцев	0,25
Более 6 месяцев	0,3

Коэффициент приоритета cij зависит также от степени оценки кредитного суждения gi и значимости банка µi и рассчитывается по формуле wS ai+giZQi

^СИ = "‘"455,                                                ₈                       (8)

где g i - степени оценки кредитного суждения i -го банка, g j = 1 — -^ ; R i - показатель уровня обеспечения БГ по заявке.

Коэффициент значимости банка µ j банка зависит от общего годового объема БГ, выдаваемого банком, и процентной ставки по продукту БГ:

_   1

^ 7               ,

^тах 'ср где Vmax – максимально возможный объем продукта БГ i-го банка; Tср – усредненный показатель годовой процентной ставки по продукту БГ.

В результате получаем

^Z a_z+(1- f^ )Sq i

= KmaxTcp----^sJ--- .                                                           (9)

^lJ                100

Для того чтобы избежать погрешности при распределении заявок между банками, вводится допустимый коэффициент погрешности β = 0,0025.

Далее матрица c ij будет постоянно уточняться в процессе многократного применения построенного по такой методике алгоритма определения коэффициента приоритета по результатам каждого проведенного выбора, так как весовые коэффициенты непрерывно корректируются самой программой обработки результатов выбора решения по «опыту» всех ранее выполненных распределений, и система будет самонастраивающейся. Результаты расчета приведены в таблице.

Фрагмент результата расчета коэффициента c ij

№        c ij       №        c ij       №        c ij       №        c ij       №	c ij
1       0,625      11      0,75      21    0,803279    31       0,6       41	0,666667
2    0,671642    12   0,765957   22    0,670103    32    0,54902    42	0,552632
3      0,6875     13    0,810345    23     0,8125     33    0,729167    43	0,606061
4    0,677419    14      0,76      24    0,756757    34    0,736842    44	0,842105
5       0,6       15     0,625     25      0,875      35    0,666667    45	0,666667
6       0,8       16      0,8      26    0,777778    36    0,791667    46	0,647059
7      0,575     17    0,830508    27    0,71875    37    0,576271    47	0,613636
8    0,645833    18    0,764706    28    0,763158    38      0,75      48	0,72973
9    0,652174    19    0,882353    49      0,75      39      0,84      49	0,666667
10    0,571429   20   0,736842   30    0,869565    40    0,785714    50	0,545455

Реализация

Предложенное решение автоматизации процесса распределения заявок на получение БГ было реализовано в среде Service Hub. Количество нераспределенных и отправленных на повторное рассмотрение заявок составило 8–5 %. Информационная модель обработки заявки представлена на рис. 4.

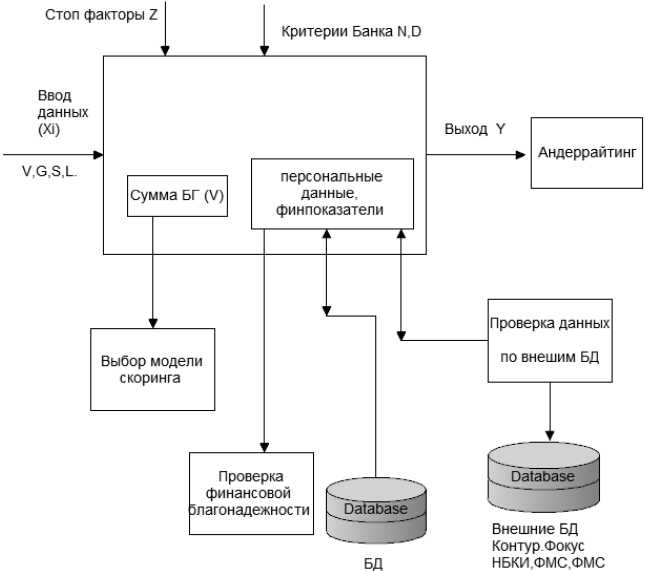
Рис. 4. Информационная модель

Управление в социально-экономических системах

Ежемесячно обрабатывается около 400 заявок, которые клиенты заводят самостоятельно, 3000 заявок заводятся посредством клиентского сервиса и 6000 заявок заводятся региональными агентами. Результаты деятельности (июль 2017 – июнь 2018) представлены на рис. 5.

Динамика доли выданных заявок в сегменте 0–150 млн руб.

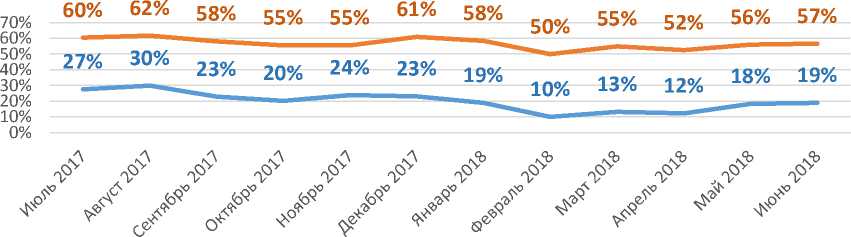
^^^^^ ■ i по сумме        по количеству

Рис. 5. График динамики выданных заявок (июль 2017 г. – июнь 2018 г.)

На графике в процентах указана доля выданных заявок по сумме / по количеству , посчитанная как отношение суммы всех поступивших заявок / количества всех поступивших заявок к сумме выданных заявок / количеству выданных заявок на конкретный месяц.

Итого динамика доли выданных заявок Service Hub по сумме (за период) – 19 %, динамика доли выданных заявок Service Hub по количеству (за период) – 57 %, реальный потенциал по количеству заявок – 43 %.

Заключение

В результате проведенного исследования была проанализирована проблема распределения заявок в условиях неопределенности. Предложенная математическая модель применена к задаче распределения заявок на банковские гарантии в мультибанковской среде с учетом специфики банковских показателей, влияющих на положительное решение. Разработанная модель внедрена в онлайн-сервисе.