Информационные технологии в иерархических мониторинговых сетях

Введение. В настоящее время в мире создан ряд глобальных информационных сетей, предназначенных для мониторинга природных и техногенных процессов в интересах защиты окружающей среды, в социальных и научных интересах. Примерами такого рода сетей являются всемирная сеть сейсмического мониторинга IMS (International monitoring system), предназначенная для регистрации землетрясений, цунами, ядер-ных и промышленных взрывов [1], происходящих в различных районах Земли; глобальная океаническая сеть GOOS (Global ocean observing system), предназначенная для слежения за различными физическими процессами в океанах; глобальная цифровая сейсмическая сеть GDSN (Global digital seismograph network) [2], используемая для мониторинга землетрясений, цунами и т. д. На рис. 1 показана схема всемирной сети IMS, имеющей в своем составе 338 наземных и морских автономных станций, снабженных спутниковыми каналами передачи непрерывно регистрируемой информации.

Несмотря на специфику задач, решаемых каждой из сетей, можно выделить некоторую общую архитектуру их построения, приведенную на рис. 2. На рис. 2 видно, что по своей организации сеть является иерар- хической и характеризуется наличием трех уровней: нижний уровень - это датчики физических процессов совместно с промежуточными центрами сбора данных (автономные станции), средний уровень – локальные центры сбора и обработки данных на уровне региона, верхний уровень - глобальный центр сбора и обработки данных на уровне страны, мира.

Рис.1. Международная система сейсмического мониторинга: точки - станции, распределенные по Земному шару

В основе мониторинга различных природных и техногенных катастроф лежит решение обратной

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (коды проектов №07-07-00214а, 09-07-12075).

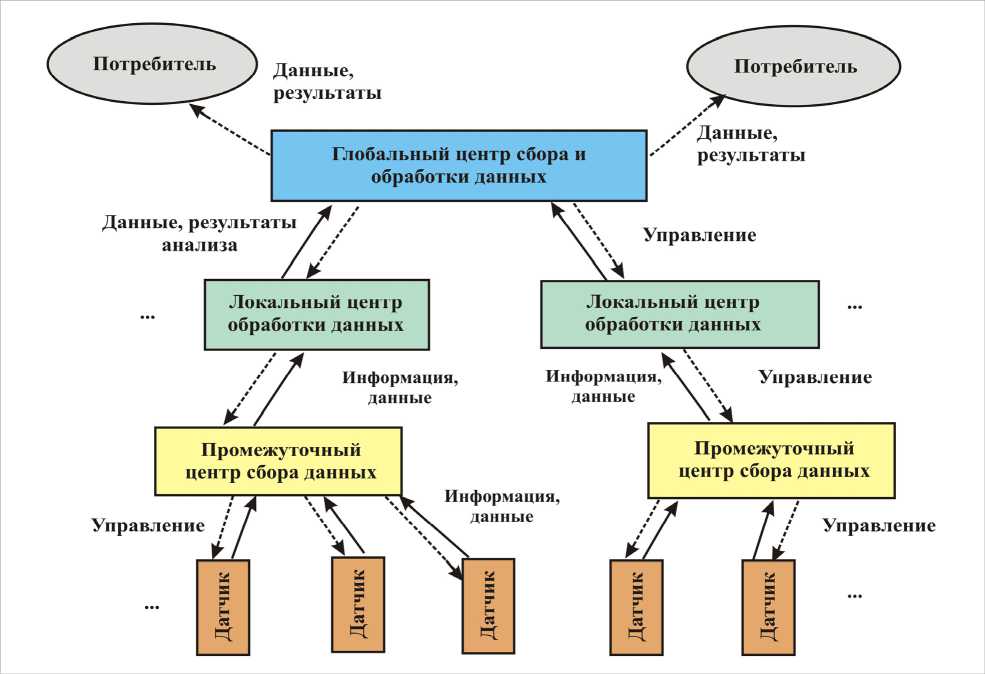
Рис.2 Архитектура геомониторинговой сети задачи восстановления параметров (географических координат, глубины, мощности, времени в очаге) источников по данным регистрации сейсмических сигналов с помощью сети сейсмических станций либо сейсмической группы.

Решение задач мониторинга распределяется между различными уровнями: на нижнем уровне осуществляется обработка регистрируемых колебаний различной физической природы (сейсмических, акустических, гидроакустических и т. д.) в реальном масштабе времени с целью определения основных характеристик упругих волн, главными из которых являются времена вступлений различных типов волн и их уровней. На верхних уровнях решается задача определения параметров источников.

Целью настоящей работы является рассмотрение информационных технологий, способствующих повышению точности и производительности решения задач мониторинга на разных уровнях в условиях воздействия внешних шумов.

Постановка задачи. Задача оценивания неизвестных параметров источника сводится к решению нелинейной системы условных уравнений [3]

t = n ( X , ^ ) + £ , (1)

где t = (t1,t2,k,tN) - вектор времен пробега сейсмических сигналов; n(X, ^) — N-мерный вектор вычисляемых времен пробега (теоретический годограф), или функция регрессии; £ = (е1,к, eN) T - вектор невязок; 0 = (x, y, z, v, t) T - m-мерный вектор оцениваемых параметров; X = (Xi,x2,к,xn) — матрица координат датчиков (или точек излучения); N - число датчиков (или точек излучения). В качестве оцениваемых параметров выступают пространственные координаты источника x, y, z, скоростная характеристика среды v и время в источнике t. В ряде случаев скорость в среде является известной. При оценивании параметров используются сведения о распределении ошибок Ei = ti (xi,0) - n(x ,, 0). Далее будем полагать, что е i - взаимно независимые случайные величины, имеющие распределение с нулевым средним и заданными дисперсиями: Eei = 0, Eeiej = ^Oj, ^i = ^(xi), (5j - символ Кронекера, i = 1,2,...,N). В случаях затруднений с заданием дисперсий принимают их равными и получают несмещенную оценку дисперсии наблюдения с единичным весом по ходу решения задачи.

Решение уравнения (1) сводится к решению обратной задачи. При этом точность решения зависит, в первую очередь, от ошибок оценивания вектора времен t = ( t 1 ,1 ₂, к , t_N ) , скорости v, шумов измерения S = ( ^ 1 , к , £ n ) T , выбора геометрии расстановки датчиков на дневной поверхности Земли. С учетом этого решение поставленной задачи делится на несколько основных этапов:

• 1)    обнаружение и измерение времен вступлений волн на фоне внешних шумов;

• 2)    расчет параметров источника;

• 3)    отображение координат источника на цифровой карте местности.

На первом этапе, реализующемся на нижнем уровне структуры сети (см. рис. 1), существует большая потребность в автоматизированной технологии решения задач в реальном масштабе времени. Такая технология позволяет снять с оператора необходимость выполнения множества рутинных операций обработки данных в условиях непрерывного мониторинга событий, регистрируемых на фоне, как правило, повышенных шумов. По отношению к источникам импульсного типа, например промышленным взрывам, погрешности определения времен пробега волн определяются дисперсией оценивания времен пробега:

^ г=------ -----.                                    (2)

^т 2 А f (2 E / N ₀)

Здесь т _и , A f - длительность волнового импульса и ширина его спектра; E/N о - отношение энергии импульса к спектральной плотности внешнего шума. Из формулы (2) следует, что уменьшения погрешности можно достичь за счет увеличения соотношения энергий сигнала и шума, расширения спектра частот A f , занимаемого импульсом, а также за счет сжатия волнового импульса во времени путем приведения его к 5 -образному импульсу. Ниже рассматриваются алгоритмы решения задачи минимизации погрешностей оценивания времен с учетом соотношения (2).

Повышение соотношения сигнал – шум и оценивание времен с помощью вейвлет-фильтрации. Алгоритм повышения соотношения сигнал - шум по отношению к волновым импульсам наиболее эффективно реализуется с помощью вейвлет-фильтрации, основанной на разложении одномерного сигнала по базису, сконструированному из обладающей определенными свойствами солитоноподобной функции (вейвлета) посредством масштабных изменений и переносов. В основе вейвлет-фильтрации лежит интегральное вейвлет-преобразование:

где f ( t ) - волновой импульс;

• 1   (t - т ^

Базис функционального пространства L ²( R ) можно построить с помощью непрерывных масштабных преобразований и переносов вейвлета v ( t ) с произвольными значениями базисных параметров - масштабного коэффициента s и параметра сдвига т . Исследования показывают [4], что для аппроксимации сейсмических колебаний наиболее подходящими являются вейвлеты Добеши [5]. В качестве примера на рис. 3 приведены вейвлеты семейства Добеши 2-го, 4-го, 5-го, 8-го и 10-го порядков.

а                    б                   в                   г                    д

Рис. 3. Семейство вейвлетов Добеши: а - db2, б - db4, в - db5, г - db8, д - db10

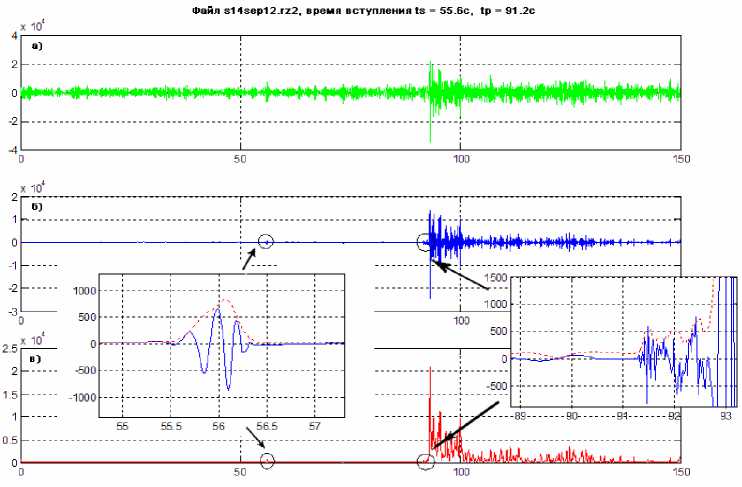
Рис. 4. Пример вычисления времен вступлений волн от двух последовательных взрывов: а - исходный сигнал, б - сигнал после удаления шума с использованием вейвлет-преобразования, в - огибающая сигнала (пунктирная линия)

Подбором порядка материнского вейвлета можно добиться наилучшего приближения. Например, по отношению к волновым импульсам, порождаемым промышленными взрывами, принято решение из вейвлетов Добеши порядков 3, 5, 8, 12 использовать вейвлет порядка 8, так как более высокий уровень вейвлета не вносит дополнительной информации и, следовательно, является избыточным. В качестве парадигмы шумоподавления с помощью вейвлет-фильтрации по отношению к сейсмическим колебаниям успешно использована трехшаговая процедура Донохо - Джонстона [6]. Для вычисления времен вступления волн в автоматическом режиме необходимо найти огибающую полученного сигнала А(t) в виде A(t) = ^ f 2(t) + f 2(t) , где f (t) = — -----dx - преобразование Гильберта. В качестве примера успешного использования расП  t - X

-да смотренной вычислительной технологии на рис. 4 приведены результаты обнаружения волновых импульсов от двух последовательно проведенных взрывов мощностью 4 и 12 тонн с интервалом между ними 52,843 с. Записи произведены в точках, удаленных на расстояния 230 и 240 км от источников. Исходная запись взрыва в полосе частот 1÷10 Гц приведена на рис. 3,а. На рис. 4 показан процесс обнаружения прихода волн с помощью вейвлет-преобразования. Выделенные фрагменты отображают моменты вступления сейсмических волн от первого и второго взрывов. Заметим, что на исходной сейсмограмме (рис. 4,а) первая волна не обнаруживается. Погрешность оценивания времен вступления оценивалась по калибровочным временам пробега волн для данного региона и составила 0,9 %.

Особенность рассматриваемого подхода обусловлена тем, что эффективность использования вейвлет-фильтрации определяется согласованием базиса функционального пространства L ²( R ) в (3) с моделями волновых импульсов. В то же время с учетом вариабельности форм волновых импульсов, получаемых от сейсмических источников разного вида, обнаружение и измерение выполняются в условиях априорной неопределенности параметров сейсмических волн. В данной ситуации эффективное решение задачи возможно на основе использования алгоритмов обнаружения типа "разладки". Рассмотрим пример практического применения такого подхода к решению задач типа (1).

Оценивание времен вступления волн с помощью алгоритмов "разладки" . Такой подход основан на применении алгоритма определения момента разладки случайной временной последовательности по максимуму специально формируемой решающей функции, представляемой в виде ряда функции авторегрессии со скользящим средним [7]. При этом случайная последовательность x 1 , x 2 ,...,х M образуется дискретными от-

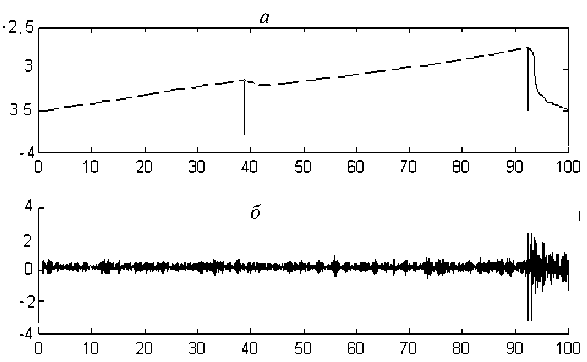
Рис. 5. Пример вычисления времен вступлений волн от двух последовательных взрывов: а - вид решающей функции, б - искомая запись шума и двух волновых импульсов на его фоне (первая волна на фоне шума не видна)

счетами "фонового" шума и волнового импульса. В рамках данных предположений на первый план выдвигается задача гарантированного обнаружения моментов разладки. В основе процедуры обнаружения лежит последовательный алгоритм кумулятивных сумм (АКС), основанный на аппроксимации участков чистого шума и волновых импульсов моделями авторегрессии проинтегрированного скользящего среднего (АРПСС) [7]. В случае если наблюдается последовательность гауссовых случайных величин Xi, решающая функция, по которой оцениваются времена вступлений волн, имеет вид g0 = 0, АgN = F(ф,,...,Фp, a;),

где

АgN =

• ^{1    -} E ф

i =1

q

• ¹ 1    - E ф .

V      i =1

N ( m 0 ) ,

( g ) ⁺— max (0 ,g ) ; ф 1 , к , ф p - коэффициенты авторегрессии порядка p ; ф _х ,...,^ q - коэффициенты сколь-

_ 2

зящего среднего; £_N - независимая гауссова случайная последовательность; a_е - дисперсия случайных значений ряда X i . При этом правило подачи сигнала о разладке t p = inf { t : g N >  h} ( h - пороговый уровень ) . В качестве примера на рис. 5 приведены решающая функция g N (верхняя часть рисунка), соответствующая исходной записи шума, и два волновых импульса на его фоне от двух последовательно проведенных промышленных взрывов (максимумы решающей функции определяют времена вступлений волн).

Результаты практического использования обеих вычислительных процедур при обработке данных, полученных от множества промышленных взрывов Кузбасса, показывают, что при приблизительно одинаковой точности оценивания времен (различие в пределах 1 %) алгоритм кумулятивных сумм имеет значительно более высокую вычислительную трудоемкость. Соответствующие оценки приведены в работе [4]. Снижение вычислительной трудоемкости является принципиально важным в условиях поточного измерения параметров волн, особенно при обработке данных в реальном масштабе времени.

Сжатие волнового импульса. Как показано в (2), погрешность оценивания времен вступлений волновых импульсов в числе прочих факторов также зависит от длительности импульса. В связи с этим возникает задача временного сжатия волнового импульса ft ) на фоне внешнего шума n ( t ) c использованием линейного оператора вида y ( t ) = L { ft ) + n ( t )} таким образом, чтобы в результате преобразования получить д -образный импульс. Такое преобразование достигается с помощью обратной фильтрации Колмогорова - Винера. Импульсная функция обратного фильтра h ( i ) , ( i— 1,2, ... N ) определяется в результате решения интегрального уравнения Колмогорова - Винера вида

N -1

E h (i)[ bf (i - j) + bn (i - j )] = bf (- i),                         (4)

j =0

где b f ( i ) , b n ( i ) - автокорреляционные функции волнового импульса и шума. Выражение (4) описывает систему линейных уравнений порядка N . Решение системы стандартными методами требует N ² ячеек памяти

10

5

-5

-10 0

а

5

10

15 Гц

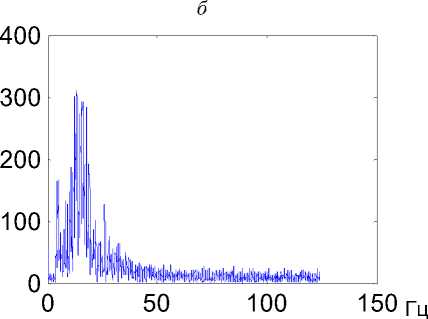
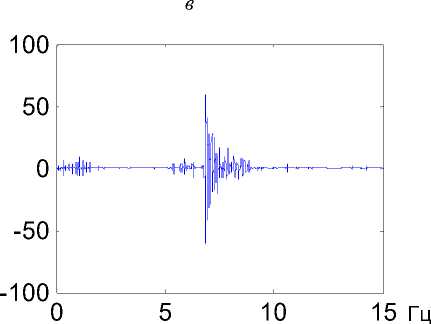
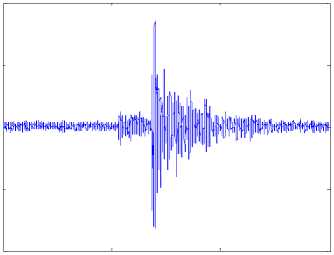
Рис.6. Результат комбинирования вейвлет- и обратной фильтрации:

а , б - запись исходной волновой формы и ее спектр; в , г

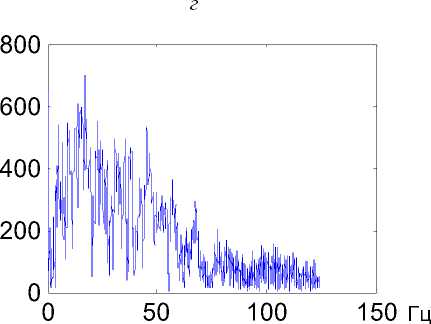
запись сжатой волновой формы и ее спектр

для хранения матрицы коэффициентов, а затраты времени пропорциональны N ³ . Как известно, одним из способов ускорения решения системы в случае высокого порядка N является использование алгоритма Левинсона, позволяющего сократить обе характеристики в N раз. Суммарная трудоемкость решения уравнения (4) составляет O ( N 2 ) + 2 O ( N log N ) + 2 N . Для иллюстрации результата работы алгоритма в виде комбинации вейвлет- и обратной фильтрации на рис. 6 приведены записи волновых импульсов, соответствующих низкоамплитудной сейсмической и высокоамплитудной акустической волнам, зарегистрированным при промышленном взрыве ( а , в ), а также соответствующие им амплитудные спектры ( б , г ). В результате применения комбинированной фильтрации ширина спектра сейсмической волновой формы увеличилась с 10 до 50 Гц (в 5 раз), отношение сигнал - шум возросло также в 5 раз, что многократно увеличивает точность измерения времен вступлений волн.

О восстановлении параметров источника. Задача оценивания параметров θ в уравнении (1) является частью так называемого регрессионного анализа, а ее решением служат оценки метода наименьших квадратов:

N

О еО

= 1

Для отыскания минимума функционала Q ( θ ) применяют итерационный метод Гаусса - Ньютона или его модификации, основанные на линейной аппроксимации функции регрессии в окрестности точки θ ^k [2]:

где

J(X,0)=

^Sn(Xi, 0) dn(Xi, 0) к   dO   , dO2

dn(Xi, 0) dOm

i = 1,2,k, n.

Оценки θ находят как результат реализации итерационного процесса ( 0 = lim 0 k ) : k ^^

где y ( X , 0 ) = ( t - n (X , 0 )) ^T ; a - параметр регуляризации; I - единичная матрица.

Другой подход к решению задачи (5)-(7) состоит в непосредственном решении системы (6) c использованием метода псевдообращения (или обобщенного обращения), основанного на сингулярном разложении (SVD-разложении). В современных версиях системы "MatLab" имеется встроенная функция svd( A ) [8], реализующая это разложение для произвольной матрицы A : svd ( A ) = [ U,S,V ] . Используя данное обращение, можно получить матрицу U , которая состоит из ортонормированных собственных векторов, соответствующих наибольшим собственным значениям матрицы А*А^Т ; матрицу V , состоящую из ортонормированных собственных векторов матрицы А^Т*А ; матрицу S , являющуюся диагональной матрицей и содержащую неотрицательные значения квадратных корней из собственных значений матрицы А^Т*А (сингулярные числа). Получаемые таким образом матрицы удовлетворяют соотношению A=U*S*V^T . В рассматриваемом случае в роли матрицы U выступают измеренные времена пробега волн, содержащие ошибки измерений; в роли матрицы V - оцениваемые параметры. Применительно к (6) SVD -разложение запишется в виде

J ( 0 ^k , x ) = U_k S k V k^T .

Недостаток данного метода, как и других методов, связанных с обращением и умножением матриц, состоит в том, что он позволяет решать системы только с малым числом неизвестных. Это обусловлено следующими факторами: с увеличением числа уравнений увеличивается число ошибок, связанных с умножением матриц; время счета растет пропорционально N ³ ; память для хранения ковариационных матриц пропорциональна N ² . В этом случае более эффективным может оказаться итерационный метод оценивания Качмажа [9, 10]. Пусть заданы дисперсии для входных параметров и для неизвестных. Тогда решение можно получить с использованием следующей рекуррентной формулы оценивания:

где

Y ( k+1) xj

=xkj+aij

^ti =ti - П (xk); k = i + n (l -1)

( ” 2 ) k

m ui             ij xj k=1

Δtk ki

– номер шага уточнения (не является показателем степени);

Особенностью данного метода является то, что он не накапливает ошибок округления и позволяет решать системы с большим числом неизвестных.

Сравнительный анализ двух данных методов выполнен на примере решения задачи локации промышленных взрывов с помощью набора пятнадцати пространственно распределенных сейсмодатчиков. Сравнивались скорости сходимости оценок и точности локации, определяемые невязкой вычисленных координат источника по отношению к истинным. Показано, что метод Качмажа дает более высокую точность определения положения источника при более низкой скорости сходимости по сравнению с SVD-разложением. В частности, при использовании метода Качмажа на 2000 итерациях невязка составляет 45 м, при использовании SVD-разложения на 500 итерациях невязка равна 100 м, причем дальнейшее увеличение количества итераций не приводит к уменьшению невязки.

Программная реализация вычислений на нижнем уровне иерархии сети. Как отмечено выше, на рассматриваемом уровне обработки данных главным требованием является обеспечение высокой производительности вычислений. Это необходимо в условиях поточной обработки регистрируемых данных в реальном масштабе времени. Большие перспективы открываются за счет использования средств вычисления на основе GPU (Graphics processing unit - графическое вычислительное ядро) [10], которые являются дополнением к универсальным процессорам CPU и позволяют многократно увеличивать производительность обработки данных, основанных на применении высокораспараллеливаемых алгоритмов вычислений. На рис. 7 приведены графики роста производительности GPU современных типов и производительности многоядерных процессоров примерно того же поколения. Видно, что различие достигает порядка и имеет тенденцию к непрерывному увеличению.

Для иллюстрации возможностей ускорения вычислений с использованием GPU оценена их производительность по отношению к некоторым наиболее часто встречающимся алгоритмам обработки данных. (Исходный объем сейсмических данных выбран равным 106.) Результаты вычислений приведены в таблице. Как следует из таблицы, на алгоритмах с высоким распараллеливанием (БПФ, свертки) производительность вычислений увеличивается на порядок и более.

При вычислениях аппаратная платформа была представлена двухъядерным CPU ПIntel Core 2 Duo (2,4 ГГц, кеш-память 3 Мб, частота шины 1066 МГц, графический процессор представлен видеокартой NVIDIA GeForce 9400M, содержащей 16 вычислительных блоков (это достаточно мало, современные видеокарты в среднем обладают сотнями вычислительных блоков)). В этом варианте применения GPU с объемом памяти до 256 Мб выделяется из системной. Такая видеокарта позволяет работать с данными только одинарной точности. Такое ограничение характерно лишь для бюджетных видеокарт, более дорогие видеокарты позволяют производить вычисления с двойной точностью.

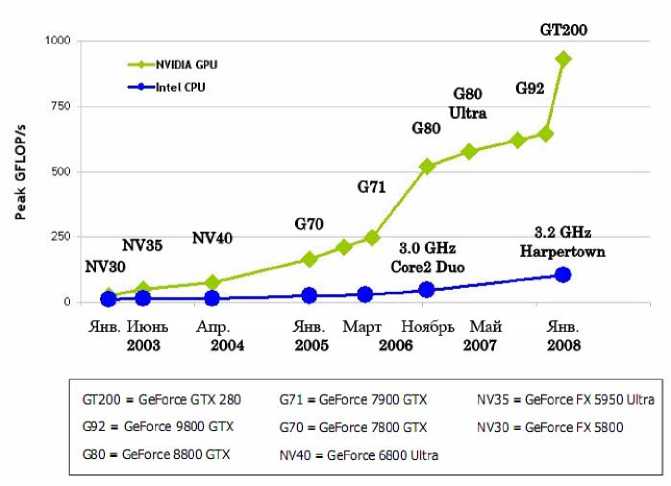
Рис. 7. Изменение производительности GPU и CPU

В качестве ОС на CPU использовалась система Windows Vista SP1. Вычисления базируются на технологии CUDA (англ. Compute unified device architecture – вычислительная унифицированная архитектура устройств) [11]. Эта технология создана компанией NVIDIA и предназначена для разработки приложений для массивно–параллельных вычислительных устройств (в первую очередь для GPU начиная с серии G80). В данном случае использовалась версия CUDA SDK 2.2 code samples for Windows Vista 32-bit.

Сравнение скорости работы алгоритмов (объем выборки 106 )

Алгоритм	Время на CPU, с	Время на GPU, с	Различие, с
Модуль быстрого преобразования Фурье	7,9872	0,6240	7,3632
Модуль взаимокорреляционной свертки	23,9616	1,8720	22,0896
Вейвлет-фильтрация	97,8134	53,8000	44,0000

Приведенные данные свидетельствуют о перспективности применения графических процессоров как эффективного средства ускорения вычислений в поточном режиме регистрации данных на нижнем уровне иерархии мониторинговой сети.

Система визуализации. Составной частью разрабатываемого комплекса является система визуализации, обеспечивающая отображение вычисленных координат сейсмических источников на цифровой карте местности. Взаимодействие между системой визуализации и системой расчета координат источника осуществляется посредством базы данных, обеспечивающей хранение информации о каждом источнике (рис. 8). В качестве ядра системы визуализации могут быть использованы известные ГИС-пакеты работы с цифровыми картами: "MapX" компании "Esti Map", обеспечивающий полную интеграцию с ГИС-системой "MapInfo", "Google-map" и др. Последовательность процесса отображения результатов следующая: после опреде- ления времен вступлений волновых импульсов и вычисления координат источников последние передаются в базу данных, после чего происходит вызов программы визуализации, отображающей сохраненные в базе данных координаты на карте. Также система визуализации может использоваться независимо, что позволяет работать с ранее полученны- ми результатами. При этом в базе данных хранится только сейсмологическая информация об источнике, а цифровая карта хранится в системе визуализации. Это позволяет отображать одни и те же сейсмические данные на различных картах без каких-либо дополнительных затрат, а также использовать одни и те же сейсмологические данные в различных системах визуализации.

На рис. 9 приведен пример визуализации карьерных взрывов Кузбасса и регистраторов.

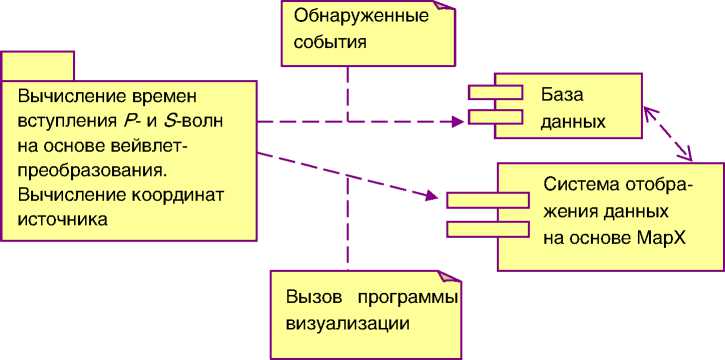
Рис . 8. Схема взаимодействия компонентов системы визуализации

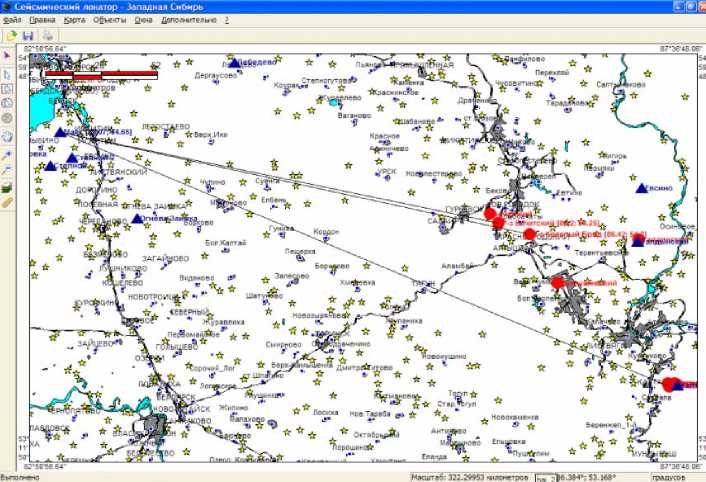
Рис. 9. Визуализация карьерных взрывов Кузбасса и регистраторов:

кружки - взрывы, треугольники - регистраторы

Заключение. Рассмотрены основные задачи информационных технологий, лежащих в основе современных глобальных мониторинговых сетей, предназначенных для слежения за природными процессами прежде всего в сейсмовулканоопасных районах, а также за техногенными процессами, связанными с проведением ядерных испытаний, промышленных и полигонных взрывов, разрушительных процессов на ГЭС, АЭС и др. Предложены алгоритмические подходы к оперативному решению задач и пути их реализации, способствующие повышению точности и производительности вычислений на разных уровнях иерархии сетей. Повышение помехоустойчивости и точности вычислений на разных уровнях иерархии сетей достигается за счет комбинирования вейвлет- и обратной фильтрации, увеличение производительности обработки данных на порядок и более – на основе использования графических процессоров GPU. Эффективность предложенных подходов подтверждена результатами обработки зарегистрированных сигналов от промышленных и полигонных взрывов.

• 1.    З ЕРБО Л. Возможности подготовительной Комиссии ОДВЗЯИ отслеживать соответствие Договору о всеобъемлющем запрещении ядерных испытаний / Докл. 5-й Междунар. конф. "Мониторинг ядерных испытаний и их последствий", Боровое (Казахстан), 4-8 авг. 2008.

• 2.    K HAIRETDINOV M. S., O MELCHENKO O. K., S EDUKHINA G. F., W OSKOBOYNIKOVA G. M. A computing technology to determine the parameters of the borehole bottom and medium // Bull. Nov. Comp. Center. Math. Model. In Geoph. 2005. Iss. 10. P. 19-26.

• 3.    Х АЙРЕТДИНОВ М. С., К ЛИМЕНКО С. М. Программная система автоматизированной локации и визуализации сейсмических источников / Вестн. НЯЦ РК. 2004. С. 70-76.

• 4.    М АЛЛ С. Вейвлеты в обработке сигналов. М.: Мир, 2005.

• 5.    D ONOHO D. L. De-noising by soft-thresholding // IEEE Trans. Inform. Theory. 1995. N 3. P. 613-627.

• 6.    Н ИКИФОРОВ И. В. Последовательное обнаружение свойств временных рядов. М.: Наука, 1989.

• 7.    Л АЗАРЕВ Ю. Моделирование процессов и систем в Маtlab. Б. м.: Питер, 2005.

• 8.    К ОЧНЕВ В. А. Адаптивное прослеживание сейсмических волн и оценка их параметров // Геология и геофизика. 1983. № 2. С. 95-104.

• 9.    Н АТТЕРЕР Ф. Математические аспекты компьютерной томографии. М.: Мир, Б. г.

• 10.    Продукты Nvidia. [Электрон. ресурс] / http://www nvidia.ru.

• 11.    CUDA Zone/ NVIDIA Corporation. [Электрон. ресурс] / http://www nvidia ru/object/cuda_home_ru html.

Марат Саматович Хайретдинов – д-р техн. наук, главн. науч. сотр.

Ин-та вычислительной математики и математической геофизики СО РАН;

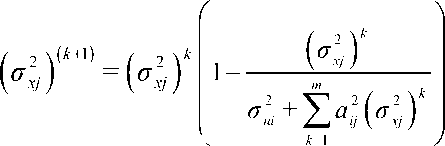
к