Information technology of targeting: optimization of decision making process in a competitive environment

Published Online December 2017 in MECS

At the present stage of the implementation of information technologies in all sectors of public life modeling of economic processes allows to predict the development of these processes and implement their adequate management. The process of making decisions on a media strategy is a complicated process. There are some effective ways to automate media planning models.

The first is the using of mathematical optimization methods which help experts to maximize the reach to the target audience, provided advertising budget constraints. However, these models require a large number of restrictions.

The second way is that simulation models based on real data about coverage of the target audience are used. The models allow to simulate the frequency of advertising contacts and the possible level of coverage with given frequency of media using. The results obtained are compared with the responses to the advertisement. The most optimal plan for an advertising campaign is the one in which the maximum ad response will be determined.

Thirdly, the most effective decision-making will be in the case of using heuristic models, although the results may be inappropriate [1]. There are models based on the use of actual data technology to scan the individual view of certain websites. This allows you to use individual data about the frequency of advertising contacts and the level of coverage, that is, to use information technology of targeting (ITT). The purpose of such models is to maximize the effective coverage of the audience, some of them trying to maximize the projected share of the advertiser's market [2, 3].

ITT can lead to a reduction in advertising costs by reducing costs that are aimed at reaching consumers who are unlikely to buy services. But ITT can also lead to higher advertising costs if efficiency gains justify increased costs [4 – 8].

A discrepancy between the possibilities of traditional methods of constructing models of distribution of advertising budget and classical media planning models and requirements for modeling and automation of decision support in managing the advertising process were found out on the basis of the analysis of the main factors of decision making on the formation of media planning, automation of the functions of targeting advertising on the market of IT services and existing models and algorithms, provided the equilibrium network for Internet advertising.

Existing approaches, in particular, the methods of mathematical programming, generally solve the problem of distribution of advertising investment in a competitive environment. However, there are no analytical studies that study the ability of firms to direct advertising to specific segments of the consumer market, there is no universal method of optimization.

The choice of criterion for each task is subjective. The degree of validity of decisions depends on the experience of the decision maker (DM) and the availability of the necessary information. Particular attention should be paid to providing DM with the necessary information and substantiation of the results obtained.

Methods of mathematical programming, in general, solve the problem of distribution of advertising investment in a competitive environment. However, there is no information technology that takes into account the features of existing advertising management systems and provides the necessary effectiveness of advertising in a competitive environment, which confirms the relevance of the solution of this problem.

To increase the efficiency of the distribution of advertising budget between different types of advertising measures by automating the decision, as evidenced by the results of the analysis of existing models and methods, there is a need to develop an improved mathematical model for making a decision on the application of ITT to advertising.

This requires the development of a mathematical model of network equilibrium in the Internet advertising and improving the methodology of making a decision on establishing the optimal size and optimal distribution of advertising budget between different types of advertising activities.

Evaluating the effectiveness of ITT during an advertising campaign will enable the development of recommendations for optimizing the placement of advertising with the help of the information technology.

• II.    Analysis of Recent Research and Publications

The problems of optimization of advertising budget were set in the works of such scientists as Kotler F., Saati TL, Nash J.F, Chatterjee P., Dafermos S., Zhao L., Lee SM, Iyer G., Rao R., and as well as other world known and Ukrainian scientists and specialists. The analysis of the main factors of decision-making on media-planning in the field of market relations was investigated by Nagorny A., Zgurovsky M.Z., Bludova T.V., Barabash O.V., Verlan A.F., Knyazevskaya N.V., Larichev O.I, Kakorin M.O, Dodonov A.G., Tupkalo V.M., Totsenko V.G., Nogin V.D., Shandra V.M. and it was shown that the set of solutions that ensure the purposeful advertising company is based on: information on the current state of the IT market; monitoring data; recommendations of expert systems; the set of given or formulated DM criteria and conditions of the advertising company; heuristic knowledge and expert group opinions [9 – 14]. According to Dafermos S., Zhao L. [15,16], the final decision develops DM who proposes alternatives and implements a choice among various alternatives, based on the evaluation of a set of often conflicting goals, such as maximizing reach to the target audience and to minimize advertising costs, which is possible only on the basis of human-machine procedures in which a person is assigned the role of the person who formulates the task, analyzes the results and makes the final decision, and the computer - the role of a complex tool that implements the whole set of methods and algorithms [18 – 21]. The basis of the methodology for solving problems at this level of the hierarchy is the systematic approach under which the advertising strategy is considered as a set of interrelated subsystems, which is an indivisible whole.

Existing mathematical models of the distribution of the advertising budget, provided the network equilibrium in general, adequately describes the existing processes, but at the same time they need improvement in the part relating to the disclosure of uncertainty for the conflict strategy.

• III.    Presentation of the Basic Material

To optimize the decision about the advertising strategy and the distribution and size of the advertising budget, the mathematical model of the competitive game and the hierarchical distribution of parameters using ball scores tables are used [7, 9, 22]. The application of game theory allows you to identify the interests of the parties, to find possible options for reconciling such interests and suggestions for forecasting events in accordance with the selection made by the parties. The game theory has a powerful device that allows to consider many different models, approaches and concepts for solving a single task. The task is not to find possible solution concepts, but to choos from all possible concepts the one that will be optimal.

Several competing companies (and i = 1, ..., n ) offer internet services with a constant marginal cost of products. The reserve value for consumers is r . It is assumed that each company has its own segment of loyal consumers, whose share is h . The size of another segment of consumer-comparators is indicated by s and is defined as s = 1-2 h . Let A be the cost of a uniform advertising covering the entire market, A h and A s – advertising costs for segments h and s , respectively, provided ITT is used, a - probability of advertising if companies use mixed advertising strategies; P – profit function; β is the probability of advertising for the segment s ; f – investments in ITT, P - probability of advertising for segment 5 by company 1, a₂ - the probability of even advertising for the whole market by the company 2, Р –

A

From here, you can get the lowest cost z =----,

1 - h

since

5 = 1 - 2 h.

In the application of ITT by both companies, the profit function for the company, when advertising in the sector s will look like:

P ( p ) = hp + sp (1 - P )) + P sp (1 - F ( P )) - A ( h + s ).

profit if both companies apply a uniform advertising, Р – profit, provided that both companies use ITT advertising, Р – company profits using ITT, provided that its competitor uses uniform advertising , Р – profit of the company, which uses a uniform advertising, provided that the other firm addresses its advertising [22].

Each firm can make investments f , which are investment in research, expert market assessments, and information technology that allows you to focus advertising on individual segments of the market. This situation is simulated by means of a game in which companies simultaneously decide whether to invest in ITT, and then compete by changing volume and advertising and prices [7, 8]. The optimal strategy is defined as a function of the capabilities of companies. The best strategies, provided both companies apply a uniform or targeted ad at a time, or when one company uses ITT, and the other advertises evenly, are described below.

In the case of uniform advertising, if equilibrium profit is zero and the probability of equilibrium is equal „*   , A - hr _T     .....        _    .             .   .

a = 1--. In addition, companies use mixed sr pricing strategies with distribution function is

The equilibrium in address advertising is defined as follows: if the advertisement can be directed and r>A , the equilibrium profit is equal to h ( r-A ) and the company advertises to its h consumers with the probability of the unit and to the purchasers-comparators with probability A

P = 1--. In addition, the company uses mixed pricing

r strategies with the distribution function:

^{F (} p )=^—x^x—; p ^e s ( r - A ) p

hr + As h + s ’

.

F * = 1 -

p ^ (1 - h ) r - A J ’

P e

A

, r

1 - h

It should be noted that if the company has set the minimum price

P ( z ) = zh + (1 - a ) zs + a zs - A = 0.

Compared to the case of even advertising, overall advertising costs are lower for targeted advertising, if rr

A < — and higher if A > — .

If company 1 uses ITT and company 2 advertises evenly: there are two possible types of equilibrium [23]: either, P <  1, a₂ = 1 or P = 1, a ₂<  1. Moreover, Company 1 will always advertise for its h segment with a probability unit. At low prices for advertising

A

0 <  A <  hr , the balance is that P = 1--, a₂ = 1. The

r profit of company 1 will be Р" = h(r - A) and the profit of company 2: P2 = rh - A(1-s). At a high cost of

r advertising, A > — the balance is that P = 1,

, A - hr „ a2 = 1--. Equilibrium profit for company 1 will be sr

P f = A - A(h + s ) at the same time the company's 2

r profit is zero. For average advertising costs hr < A < —, the balance of both types is possible. But equilibrium P < 1, a2 = 1 dominates over equilibrium with P = 1, a < 1.

Table 1. shows the company's winnings when choosing different options for investing in ITT.

Table 1. Decision to invest in ITT

	Company 2
Company 1		Uniform	Target
	Uniform	Р u , Р u	P d , P a - f
	Target	P a - f , P d	P. - f , P - f

Thus: when 0 <  A <  hr both companies will target ads if f <  Ah ; only one company will use ITT if f e [ Ah , A (1 - h ) ] ; no firm will address if f >  A (1 - h ).

When:  A > — both companies will target ads if f e [h(r - A), Ah)]; and no firm will address if f > Ah .

The results in the table. 2, show that regardless of whether advertising is uniform, or ITT is used, the profit of a company does not affect the use of ITT prices [24, 25].

f <  h ( r - A );  only one firm will address if

Table 2. Equilibrium profit as a function of ITT: the probability of segmentation advertising for a profit margin

Adve-rtising	Case1 Uniform advertising Uniform pricing	Case 2 Targeted adverti-sing Uni-form pricing	Case 3 Uniform advertising Tar-geted pricing	Case 4 Targeted advertising Targeted pricing
Seg-ment h	A - hr 1 sr	1	A - hr 1 sr	1
Seg-ment s	A - hr 1 sr	1 - A r	A - hr 1 sr	1 - A r
Pro-fit	0	h ( r - A )	0	h ( r - A )

With target price formation, the price for h segment is r , and the price for segment s is established using mixed strategies [26].

In the case of continuous advertising at any given intensity of advertising, each consumer of the target segment will see advertising with probability y

.

Advertising costs are proportional to the size of the segment and is a growing and convex quadratic function on the part of the segment for which the information is assigned, the function of advertising costs under the ITT k can be written as follows: A = qyQVj where j = 1, 2 -type of consumer, q – the volume of the segment.

In the case of even advertising, the cost function will look like A = y у ² . Let the intensity of the advertising of competitors in the segment of comparison у ( p ₀) , where p – the established value f ( p ) – the function of the density of probabilities from the competing value, and р – the lower limit of the set value.

Thus, the target function for each company is as follows:

Р = p Vy_h ⁽ p ) + y _s ⁽ p ) 5 ^{(1 -} F ⁽ p )) +

+ ' ( p ) S J (1 -y o ( p o )) f ( p o ) dp o ] - ^p

• ^- hky^ p ) ^{- S}k y S⁽ p ).

An advertising strategies for both segment h and segment s are mixed strategies, the advertising level for the h segment is much higher than for the segment s [27]. In equilibrium, the price has a positive correlation with the advertising level for the segment h and is negative with the advertising level for the segment s [28].

The condition of equilibrium can be written as follows: Р = h ^ y_h ² ( p ) + h у y_s ² ( p ). Provided that the intensity of advertising is a function of the profile of pricing, y ₀ ( p ₀) is defined as the level of advertising chosen by the competitor, which corresponds to the choice of price p . The profit function for the company can be written as follows:

P = p yh + ys ( 1 ^- F ( p ) ) + ys J ( 1 ^-y о ( p о ) )

x

^f ( p 0 ) dp 0 ^- 1 у ².

Consequently, the total profit for a uniform advertising .     .   . _t .      _w    ((1 - h ) r - A ) ²   _ .            .

is calculated as W = —----------—. This expression ua      (1 - 2 h) r determines the expected characteristics: there is an increase and r decrease over A. Total revenue in the case of ITT is calculated:

W ta =

= 1( r² - A ² - 2 hAr + 2 hA² - 2 r + 2 A + 4 hr - 4 hA ). r

The model of selection of the optimal amount of advertising on various Internet resources is considered, in order to maximize the desired reach to the target audience. The problem is modeled as a problem of target programming with random constraints, since the reach parameters are considered as random variables with known mathematical expectations and mean square deviation [30]. The parameter that corresponds to the reach can be determined by finding the ideal solution and the law on which the parameter values change.

A mathematical model of network equilibrium in Internet advertising for the competitive struggle, which provides an opportunity to determine the amount of equilibrium online budget for competing firms, as well as equilibrium budget allocations on various websites [31], has also been developed.

One and the same IT service can be advertised by N firms in all environments. For company n : n = 1,2,... N . f nw means the cost of internet advertising and f no – the cost of advertising in other means, f nw and f no n = 1,2, ... N are grouped respectively in the vectors f w and f o .

A network equilibrium model is proposed that takes into account several websites.           and

. nw w            no o indicate the reaction (feedback) of consumers as a result of costs f^  and f respectively; r (f), i = w, is a growing, differentiated and constrained function of f , each firm has a general advertising budget С . The problem of optimal budget allocation, assuming that it is necessary to maximize consumer feedback across all environments within the budget, can be written as an optimization problem:

under conditions f w + ^f n_O <  С П , f w f , > ⁰ .

f * = { f * min ; m = 1,2,..., M ; ” = 1,2,..., N } , is an equilibrium budget allocation for all firms on all websites in the sense of Nash if and only if it satisfies the following equation and inequalities for all firms n and all sites m :

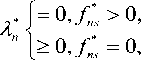
where A . is Lagrange multiplier associated with budget constraints.

Nash equilibrium conditions [9, 12, 14] for N firms competing on M websites correspond to the equilibrium conditions of the network: N is a network of N +1 nodes, and N ( M +1) bonds, and with N pairs beginning / target ( P / M ), which are connected by M paths and "fictitious" way. Thus, there are all N ( M +1) paths in the network. The path flow vector is set to f = ( f 11 , f 12 , .. ., f MN )^T, which is a vector in R^{MN +} , where f mn is the flow in the path mn . Flows f ns : n = 1,2, ..., N are integral to the corresponding false paths and correspond to the reserve or unused part of the budget. u_mn ( f ) means the marginal revenue from the network flow f in the path mn and is determined as follows:

u mn ( f ) = -rn 7 f ²; m = 1,2,-, M ; ” = 1,2,- ^{5 f} mn

N , while all

marginal returns on the false path are considered zero. The demand elasticity associated with the n-th pair P/M is presented by b_n ( . ) for n = 1,2,..., N . Then the equilibrium conditions have the following interpretation for the equilibrium of the network: only those paths that provide maximum marginal profit, that is, the maximum marginal feedback is used (with positive flow) in equilibrium. These equilibrium conditions are opposite to the conditions for the problem of the network equilibrium of the transport network in the classical case, as well as in the form of variational inequalities in the asymmetric case, when the equilibrium conditions can not be reformulated as the Kuhn-Tucker conditions and the related optimization problem [32]. In problems of the equilibrium of the transport network, only those paths connecting the pairs of P-M , which have minimal transport expenses are used in equilibrium [14]. The demand is equal to the sum of trajectory streams, in the path that connects each pair. In the case of the equilibrium problem of an Internet marketing system, marketers try to maximize feedback one-sidedly, and the marginal feedback is maximized / equalized with the equilibrium of used web-sites. The flows in the network model correspond to flows of financial resources and demand (requirements) in turn are the budgets of firms.

The optimization problem of the advertising budget distribution is formulated through variational inequalities for equilibrium conditions in the sense of Nash [15], which allows not only to take into account the optimization of the response, but also to obtain an equilibrium budget distribution as a consequence of this optimization [33].

Since the company's online advertising budget b_n ( A ) is a growing function of the λ_n boundary response, then A = A ( b ) is a reversed function to b_n ( . ) and is also       an       increasing       function.       Let

U ( f ) = ( U mn ( f ) ; m = 1,2,..., M ; ” = 1,2,..., N ) , ^

u ( f ) eR M ¹ , beR ⁿ^ i A ( b ) eR ” b = ( bn ; n = 1, 2,..., N) i A ( b ) = ( A ( b „); ” = 1,2,..., N) respectively. Equilibrium conditions can be written in the equivalent form: for all firms n = 1,2, ..., N and for all websites m = 1,2, ..., M :

5 T n ( f ’)     ^A ” ^{( b} ” ) , ^fmn

5 f mn   [< A ” ( b ” ) , f m”

> 0,

= 0,

, /, .x ;= o, f*s >  o,

”( ” )[>0,/*

, ns ,

M

**   *

/J mn    f ns n ⁽ n ) .

m = 1

Now the equilibrium of Nash in the Internet advertising can be formulated in the form of variational inequalities as follows: the vector ( f *, b* ) g K¹ is in equilibrium if and only if it is a solution of the variational problem:

U"(f *), f - f *^-(4b*),b-b^ < 0, for V( f, b)6 K 1, where

K¹ - { ( f , b )|( f , b ) eR MN ⁺ N

1X + f™ = b „ , Ms >  0; n = 1,2, - , N } m = 1

and <.,.> means the internal product in the Euclidean space of the required dimension, which is a variational description of the inequality

MN NM m=1 n=1 n=1 m=1

X ( b n - b * )) <  0,( f , b> K 1 .

From the marketing point of view, it is advisable to consider the K ¹ convex, limited compact set, since the company's online budget b is less than or equal to the company's overall advertising budget, which in its turn can not be infinite (hence unlimited).

In [32] the existence and uniqueness of the solution of the variational problem was proved, and algorithms were developed for calculating equilibrium advertising budgets and the distribution of the budget.

The effectiveness of alternative advertising strategies in conditions of competition and incomplete awareness is found through point and interval estimates of the results of decisions on the application of a strategy in the case of anticipated actions of a competitor, which is the value of the utility function on the set of outputs. As an utility function of the company, the total profit Р is chosen, since it can easily be reduced to a monetary measure, therefore Е ( x ) = [ P_a ( z ) ] . The results z_k ( k = 1 ,...т ) of the strategy selection x..^i = 1,..., n ) have utility Р ( z j ) = g ^kj ( x i 1 ; x j ₂), i = 1,.., n ; j = 1,..., n and lead to a guaranteed profit g ^* . Then the economic efficiency of using each strategy can be found by the formula:

E ( x ) = max Р ( z_k ) . k ^k

To overcome the uncertainty of the behavior of opposing companies, two approaches are used: targeting achievement of the guaranteed result in the worst conditions and targeting the most likely variant of the behavior of the competing company and provide for itself the best result under these conditions [34]. That is, the following advertising parameters are selected in order to have the maximum possible value of the target function in the worst case scenario. In this case, the criterion used to find guaranteed earnings for each of the competing companies is:

g * = max min g 1 ( x 1 , x 2 ), ^x 1 ^x 2

g * = max min g ₂ ( x _t, x ₂). x ₂ x 1

Then for the first company it is guaranteed that for х = х_г * and any value of x₂ the condition g ₁ ( x\ x ₂) >  g * . is fulfilled. And for the second company, х₂ = х * at any value х_т , the condition g_x ( x , x * ) >  g * . is fulfilled.

A tabular, graphical, or classical method based on the study of extreme properties of functions can be used to find guaranteed earnings [35].

To find the absolute minimum and maximum of the functions used in the interval comparison method, another criterion is used:

g ⁺ = max max g 1 ( x , , x 2 ), x ₁ x ₂

g 2 ⁺ = max max g ₁( x 1 , x 2 ), x ₂ x ₁

g - = min min g ₁( x„ x 2 ), x ₁ x ₂

g 2 " = min min g ₁( x_v x 2 ). x ₂ x ₁

The situation is estimated by the value of the target function in the numerical interval, the minimum value of which corresponds to the worst situation, and the maximum – the best [35, 36].

For     the     target     function     of     each company gtj. (x1, x2), i, j = 1,..., n, the interval score is presented as:

¹ 1 ^{( x} 1 , x 2 )

g 1^{( x} 1 ,^x 2 ) - g - .

g 1 ^+- g -

1 1 ⁺ ( x , y ) =

g 1 ^+- g 1 ( ^x 1 , x 2 ) .

g 1 ^+- g -

I - ( x 1 , x ₂) =

g 2 ^{( x} 1 , x 2 ) ^- g 2 - .

g 2 ^+- g 2

¹ ₂ ( ^x 1 , x ₂ )

g 2 ⁺- g 2 ^{( x} 1 , x 2 ) g 2 ^+- g 2 -

Here, Ix , 12 , I+, I+ are the estimates that determine the relative level of differences in utility functions from their minimum and maximum values, respectively g1 ^ g1(x1,x2) ^ g1+; g2 ^ g2(x1,x2) ^ g2+.

It is easy to verify that I - + 1 + = 1; I - + 1 + = 1. It is enough to get one estimate for each function and predefine it, or set the permissible lower limit.

Taking into account the above assumptions, we can show the dependence of the profit on advertising costs on the graphs presented in Fig. 1

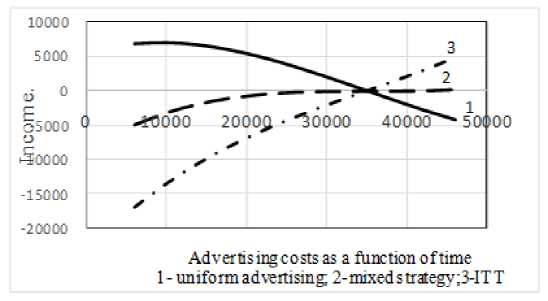
Fig.1. Dependence of profit on advertising costs

Thus, in order to assess the effectiveness of alternative advertising strategies in conditions of incomplete certainty, we need:

• -    to identify outputs for each strategy;

• -    to build the function of the total profit on the set of

results of the application of each strategy;

• -    to calculate its guaranteed and absolute boundary values for each strategy,;

• -    to perform interval comparison as it is shown in

Fig.2.

й о

о га

1  3 5 7 9 11 13 15 17 1921 23 2527

Time Period

Fig.2. Dependance of customer`s response on advertising activity

The use of the maximizing criterion for finding guaranteed earnings will be more reliable since probabilities of the environment states appearance are precisely unknown,. The best alternative is the one with the smallest element. The alternative chosen by this criterion completely excludes risk. In order to find the absolute maximum and minimum, respectively, the maximum and minimum criteria are used. The best alternative will be the one in which the maximum element is the greatest and the minimum element is the smallest. That is, the alternatives that give extremes to these expressions are optimal.

The accuracy of evaluating the effectiveness of advertising with the proposed method depends on the quality of developed research of the relevant parameters.

• IV. Conclusions

The distribution of the advertising budget optimization problem is formulated through variational inequalities for the equilibrium conditions in the sense of Nash. This allows not only to take into account the optimization of the response, but also to obtain an equilibrium budget distribution, as a consequence of this optimization.

The proposed mathematical model allows to automate the decision making on the use of ITT when planning the company's advertising strategy in the IT market. In particular, the improved method of automation of decision-making is oriented on continuous advertising and allowed to develop proposals on the strategy of media planning, taking into account the specifics of the market of IT services and the nature of solving management tasks. The algorithms and program implementation presented in the article allowed to improve the marketing strategy of the company, namely, its advertising strategy, which provides allocation of investments according to the functional purpose of advertising platforms, taking into account the priorities of their tasks performed on the basis of ITT.