Инновационная модель оценки курса "Современные технологии логистики" на основе технологии "перевернутого класса"

• 1. Introduction

• 2. The insufficiencyof current assessment methods

  The course assessment is one of the most effective ways to test students' outcomes, which can be used to identify, regulate and promote the teaching. At the same time, it is an important link in the course teaching. Currently, like most other courses, the examining method of modern logistics technology included two parts, namely formal assessment (30%) and term examination (70%). The formal assessment is composed of attendance (30%), current results (30%) and homework (40%). However, for large groups’ teaching there is no way to make a general survey for each class. There are less students participating in class discussions, and the plagiarism phenomenon is serious. The final assessment is usually 'one test for life', and the teacher only judges by the fact that whether the students have completed the examination paper. In addition, the number of classes is small, so the teacher who might teach, give the same tests and grade work. This pattern means a course teacher has a larger subjectivity

• 3. The mathematical modelof AHP-FCE

  The analytic hierarchy process (AHP) is a structured technique for organizing and analyzing complex decisions, based on mathematics and psychology. It has particular application in group’s decision-making and is used globally in a wide variety of situations. This method makes use of both qualitative and quantitative analysis to develop the inter-relationship among the indexes and establish the judgement matrix. In parallel, fuzzy comprehensive evaluation (FCE) method is a comprehensive evaluation method based on fuzzy mathematics, which can transform the qualitative evaluation into the quantitative evaluation according to the membership degree theory of fuzzy mathematics. This method can solve the ambiguous and hard-to-quantify problems and, therefore, is suitable for solving various non-deterministic problems. Usually, the final examination uses a grading system (excellent, good, medium, passing, failing), but the definition of each level is not clear and the grade is ambiguous. So, the fuzzy comprehensive evaluation is an effective evaluation method and, particularly suitable, for the flipped classroom assessment. So, this paper combined AHP/FCE methods that provided a solution to the problem solving, which makes use of the AHP to calculate the weight values first, and, then, implement the FCE to carry out a from-quantitative-to-quantitative assessment.

Modern Logistics Technology is a basic course, highlighting major and obtaining practical significance. Therefore, this course not only imparts knowledge, but forms personal direction and arouses students' interest. Students could identify areas of interest for future study.

The flipped classroom is when the teacher puts in the information environment learning resources in the form of videos. Students watch and learn the video resources before the class. Teachers and students work together to finish the homework in the classroom, work out collaborative inquiry, discuss questions and fulfill interactive activities in a new teaching mode. As an innovative form of classroom teaching, flipped classroom has subverted the inherent mode of traditional teaching, which is a major breakthrough in teaching reform under the condition of modern information technology development. Flipped classroom changes the “studying in class + practicing after class” into “studying before class + exploring in class” in the form of reversing the two stages of learning that of knowledge transfer and knowledge internalization [1]. The realization of flipped classroom can fully exert the activity of students, improve the interaction between teacher and students, and enhance students' learning ability and cooperation ability.

Образование в странах мира and randomness, which is not favorable for improvement of teachers' level and for mobilizing students' learning enthusiasm. Furthermore, a test consists of multiple choice questions, true and false statements, fill-in-the-blanks, quantitative problems, short answers, most of which are to test the memorized knowledge, ignoring the application of knowledge and personal development. Students mostly cram for the final; even someone who never pays attention in class will try to cheat at examination. Therefore, such a single, result-oriented and subjective assessment method neither assesses the extent of students’ learning nor improves student’s thinking, values, and efficiency. It is also not suitable for a new teaching model [2].

The main process is as follows [3, 4]:

• (1) Identifying the affecting factor set

For fuzzy evaluation, factors that affect the parameter’s value determination should first be identified. If the known affecting factors are u 1 , u 2 ,..., u m , the set these parameters can make up is U = { u i ， U 2 ， ...,U m } , and this factor set is a common set.

• (2) Determining factor weights set

Each factor has a different impact on, or importance to the value determination of parameters. In other words, the factors have different weights for parameter values. The set composed of various weights of all factors for parameter value determination is called the factor weights set, which is represented as A = { a 「 a 2 ， ...,a m } . If a i represents the weight of factor No. i, the weight of each factor should satisfy Equation (1).

n

£ a i = 1,a i > 0.                          (1)

i = 1

The Analytic Hierarchy Process operation can be divided into the following five steps:

Step 1: Define the decision-making problem.

Step 2: Create a hierarchical structure.

Step 3: Create a pairwise comparison matrix. Table 1 is the evaluation measurement and relative definition of AHP.

Step 4: Calculate the eigen values.

Step 5: Conformance test.

Eigen values in step 4 can be calculated in the following ways: Normalization of the Row Average (NRA), Average of Normalized Columns (ANC), Normalization of the Geometric Mean of the Rows (NGM), and Normalization of the Average Reciprocal of Columns. The consistency test in step five is to make sure that the evaluation results are consistent when the experts are conducting pairwise comparisons, which means that the experts’ preference for criteria is transitive. Saaty suggested that consistency index (CI) and consistency ratio (CR) be used for the test. If CI and CR are both less than 0.1, it means that the pairwise matrix is consistent. If the matrix is not consistent, the equation of CI and CR is as follows:

CI J^max _ ⁿ ,                      (2)

• n — 1

入 max is the largest eigenvalue of the matrix, n is matrix order (number of parameters).

CR = CI/RI

CR < 0.1ok

C:R = Consistency ratio

C:I: = Consistency index

R:I: = Random index, (3) where n is the number of evaluation criteria; RI is random index whose value increases if the number of criteria increases, as shown in Table 2.

Table 1

Evaluation Measurement and Relative Definition of Analytic Hierarchy Process

Evaluation measurement	Definition
1	Equal importance
3	Slight importance
5	Essential importance
7	Very strong importance
9	Absolute importance
2, 4, 6, 8	Intermediate

The memberships of each single factor evaluation set constitute a fuzzy matrix, where R is called the single factor evaluation matrix, as shown in Equation (6). R is a fuzzy matrix, and it can also be regarded as a U-V fuzzy relationship matrix, called fuzzy transformation.

(5) When conducting fuzzy composition, if the fuzzy evaluation matrix of a program to an evaluation object is:

Table 2

Table of Random Indexes

Order N	1	2	3	4	5	6	7	8
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41

R 1

R 2

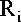
(3) Establishing a parameter evaluation set

An evaluation set is the set of various possible evaluation results given by evaluators for the evaluation objects, shown as V V = { v i ， V 2 ,…,V n } ； vi(i = 1, 2, ..., n) represents all of the possible evaluation results. The purpose of fuzzy evaluation is to obtain an optimal evaluation result from the evaluation set based on the comprehensive consideration of all affecting factors. As vi and V have the relation of common set, the evaluation set is also a common set.

(4) Building a single factor evaluation matrix

A single factor fuzzy evaluation system evaluates single factors to determine the membership of an evaluation object to an evaluation set. The evaluation object is evaluated as the No. i factor u i in the factor set, and the membership of No. j factor V i in the evaluation set is r ij , so the evaluation result of No. i factor u i can be expressed as:

Ri =曳+区+... +丛 v1v2       vn where Ri is called a single factor evaluation set. As a fuzzy subset, it can be expressed as Ri 二{3，彳2,…,％}. Similarly, the single factor evaluation set corresponding to each factor is as follows:

^R 1 = { r 11 ,^r 12 ,...,^r 1n }

^R 2 = ^{{ г}21 ， ^Г22 , …,^r 2n }

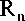
^r 11

^r 21

:

^r i1

:

rn1

^r 12

^r 22

:

^r i2

:

rn2

r1j r2j

:

^r ij

:

rnj

r1m r2m

:

(6) r im

:

r nm

then the comprehensive fuzzy evaluation with weighting considered and the product of fuzzy matrix is:

B = A ・ R = [ b i ， b 2 ,…,b j ,…,b m ]          (7)

In the above equation, the symbol “•” represents fuzzy composition. The weighted fuzzy matrix A and factor evaluation matrix R have a variety of compositions. This study will use different compositions to work out various evaluation results for comparison and analysis. The model selected is as follows:

when the composition is done by M( ・ , ㊉ ) algorithm

Г旦 〕 bj = min\ 1,£ai% };j = 1,2,…,n.         (8)

、 i = 1         ,

^R m ^{- {} r m1 ^,ri n2 ^,...^,ri nn

4. The course assessment basedon AHP-FCE

4.1. Establishment of the evaluation indicator system

On the foundation of FCE, the selection of evaluation indexes will directly affect the accuracy of comprehensive evaluation. Basing on researches of domestic and foreign scholars for the examining model and the exam outline of the course, the new examination method of the Modern Logistics Technology is as follows ： formal assessment and project result. In this paper, the evaluation system is composed of 4 indicators and 12 corresponding sub-indicators. This is shown in Table 3.

Table 3

Level A	Level B		Level C	Evaluator
Course assessment of Modern Logistics Technology	Formal assessment	Before class X1	Test performance X11	Teacher
			The quality of raising question X12	Teacher and students
			Online learning time X13	Teacher and students
		In class X2	Attendance X21	Teacher and students
			Classroom discussion X22	Teacher and students
			Classroom notes X23	Teacher and students
		After class X3	Spread and transfer the knowledge X31	Teacher and students
			Homework X32	Teacher
	Project result	Final X4	The content of the topic X41	Teacher and students
			Team collaboration X42	Teacher and students
			The quality of project X43	Teacher and students
			Question and answer X44	Teacher and students

Table 8

Judgment Matrix P4 of Level C Indicator X 4 and conclusion

P 4	X 41	X 42	X 43	X 44
X 41	1	1/2	1/4	1/3
X 42	2	1	1/3	1/2
X 43	4	4	1	2
X 44	3	3	1/2	1
Weight	0.094	0.133	0.479	0.294

入 max = 4.082; CI = 0.0273; CR = 0.0307 < 0.1, Conform to the consistency requirement

= ( 0.212 0.412 0.211 0.165 0 )

Upon normalization, the comprehensive evaluation vector is, so similarly,

A2 = ( 0.236 0.406 0.294 0.064 0 )
A3 = ( 0.200 0.400 0.250 0.150 0 )		(13)
A 4 = ( 0.184 0.298 0.264 0.254 0 )
(2) Fuzzy evaluation to the overall performance of the student
	'0.212 0.412 0.211 0.165 0 、
A = W ・ R = ( 0.296 0.478 0.069 0.157 ) •	0.236 0.406 0.294 0.064 0	=
	0.200 0.400 0.250 0.150 0
	v 0.184 0.298 0.264 0.254 0 )

= ( 0.218 0.391 0.262 0.136 0 ) .                                                        (14)