Инструментальная поддержка формальной верификации программ, написанных на языке функционально-потокового параллельного программирования

В настоящее время наблюдается тенденция к усложнению программного обеспечения и увеличению сложности его отладки и рисков в случае сбоя. становятся трудно отлаживаемыми, содержат больше ошибок, а последствия ошибки в системе могут оказаться чрезвычайно дорогими. В результате, стали активно развиваться методы верификации программ, в частности формальная верификация. Под формальной верификацией понимается доказательство корректности программы, которое заключается в установлении соответствия между программой и ее спецификацией, описывающей цель разработки [1]. При этом, соответствие программы ее спецификации устанавливается посредством строгого математического доказательства. Главным преимуществом формальной верификации является возможность формально доказать отсутствие ошибок в программе.

Наиболее универсальным методом формальной верификации является дедуктивный анализ на основе исчисления Хоара [2]. Исчисление Хоара — это расширение какой-либо формальной теории \frakI введением в нее формул специального вида, называемых тройками Хоара. Тройка Хоара — это программа, к которой приписаны две формулы теории \frakI, описывающие ограничения на входные переменные и требования к результату выполнения программы. Эти формулы называются предусловие и постусловие соответственно. {^}, где Prog — программа, а \varphi и \psi — предусловие и постусловия для Prog. Также для расширения теории \frakI вводится набор аксиом для операторов языка и правила вывода, с помощью которых из аксиом можно выводить утверждения о свойствах программ, в том числе о свойствах корректности. При этом, расширение теории \frakI строится таким образом, чтобы корректность программы вытекала из истинности тройки Хоара для этой программы. Основная идея данного подхода заключается в том, чтобы на базе аксиом, с помощью последовательных применений правил вывода, преобразовать тройку Хоара в формулу теории \frakI, и доказать истинность формулы в этой теории.

Этот метод применим для произвольных языков программирования, а основным его преимуществом является возможность частичной автоматизации процесса доказательства. Стоит также отметить, что теорий \frakI для описания спецификаций программ) для каждого языка программирования аксиомы и правила вывода будут своими, так как строятся на основе семантики этого языка. Значит каждому языку программирования будет соответствовать свое исчисление Хоара, и поэтому сложность доказательства корректности программ тоже будет различной.

В настоящее время достигнуты определенные успехи в практическом применении дедуктивного анализа для верификации последовательных программ.языках программирования Для поддержки этого процесса разработан ряд систем. В качестве примера можно привести верификатор программ на языке C Boogie [3] и систему СПЕКТР [4], а также системы для верификации объектно-ориентированных программ на Java: LOOP [5] и KeY [6].

Развитие методов формальной верификации особенно актуально для параллельного программирования. Дедуктивный анализ не нашел широко применения при верификации параллельных императивных программ из–за высокой сложности процесса. Основной проблемой является резкое увеличение сложности формальной верификации параллельной императивной программы по сравнению с последовательной. Главная причина — необходимо учитывать конфликты из-за ресурсов, например, такие как неправильное совместное использование общей памяти или взаимные блокировки процессов в случае работы с распределенной памятью.

Альтернативой императивного подхода является функционально-потоковая параллельная (ФПП) парадигма и ее реализация — язык программирования Пифагор [7, 8]. из-за ресурсов. Модель вычислений, лежащая в основе языка задает вычисления в автоматически выделяемых бесконечных ресурсах. Это позволяет не учитывать возможные ресурсные конфликты, что облегчает процесс написания функционально-потоковой параллельной программы. Каждая программа — это функция, поэтому в языке отсутствуют переменные и циклы, а операции выполняются по готовности данных. В результате, сложность формальной верификации ФПП программ сравнима со сложностью верификации последовательных программ. Другая важная особенность языка — возможность достичь максимального параллелизма программы за счет того, что параллелизм реализуется на уровне операций. После доказательства корректности такой программы, она может быть перенесена на конкретную архитектуру с конечными ресурсами, при необходимости, с ограничением ее параллелизма.

Для языка Пифагор построено исчисление Хоара [9], позволяющее доказывать корректность программ. В качестве языка спецификации выбрана логика исчисления предикатов первого порядка. программы, к дугам которого привязаны формулы на языке спецификации (дуги размечены формулами), а процесс преобразований троек Хоара сводится к разметке дуг графа формулами, модификациям графа и свертке программы. Тройка Хоара, которой соответствует граф со всеми размеченными дугами может быть преобразова- на в формулу, тождественная истинность которой будет свидетельствовать о корректности программы. Однако процесс доказательства достаточно трудоемок, так как обычно доказательство истинности исходной тройки сводится к доказательству истинности нескольких преобразованных троек. Необходимость рассматривать большое количество вариантов значительно усложняет процесс доказательства. Поэтому целью данной работы является разработка инструментальных средств, обеспечивающих поддержку формальной верификации ФПП программ.

В разделе 1 вводятся основные понятия и описываются преобразования информационного графа с разметкой. Раздел 2 рассматривается архитектура системы поддержки формальной верификации функционально-потоковых параллельных программ, которая позволяет строить дерево доказательства. Реализация предложенной системы и ее основная функциональность описаны в разделе 3.

• 1.    Преобразования информационного графа с разметкой

Программу на языке Пифагор удобно отображать в виде информационного графа — ациклического ориентированного графа, определяющего информационную структуру программы, у которого вершины представляют программо-формирующие операторы, а дуги задают пути передачи информации между вершинами [7]. Информационный граф программы, дуги которого помечены формулами на языке спецификации, будем называть информационным графом с разметкой (ИГР). Если в информационном графе размечены только входная и выходная дуги, то граф соответствует тройке Хоара, в которой программа представляется графом, разметка входной дуги есть предусловие, выходной — постусловие. Зададим над информационным графом с разметкой следующие преобразования:

• 1)    разметка дуги;

• 2)    изменение информационного графа программы:

• (a)    эквивалентное преобразование,

• (b)    расщепление;

• 3)    свертка программы.

Процесс доказательства корректности ФПП программы можно рассматривать как последовательность преобразований исходного информационного графа с разметкой, где под «исходным информационным графом с разметкой» понимается ИГР, которому соответствует исходная тройка Хоара, то есть граф у которого входная дуга размечена заданным пользователем предусловием, выходная — постусловием, а остальные дуги не размечены. Последовательными преобразованиями из исходного информационного графа с разметкой получают множество полностью размеченных ИГР , к каждой дуге такого графа приписана одна формула. Эти графы с помощью свертки преобразуются в тройки Хоара, которые можно напрямую преобразовать в формулы на языке спецификации для проверки истинности. Если все полученные формулы истинны, то и исходная тройка истинна, а программа корректна.

• 1. 1. Разметка дуг

Принцип разметки дуг графа формулами (приписывание формул к дугам) описан в [9]. Формула, приписанная к дуге информационного графа, описывает свойства данных, которые передаются по этой дуге.

Разметка дуг информационного графа осуществляется на основе аксиом для встроенных функций и теорем для пользовательских функций с доказанной корректностью. Одну функцию могут описывать несколько аксиом или теорем, поэтому в результате разметки может быть получено несколько новых графов.

На множестве формул, помечающих дуги одного ИГР, введем отношение иерархии, назвав формулу, помечающую дугу (a, b), родительской по отношению к формуле, помечающей дугу (b, c) для узлов a, b, c графа.

При разметке дуг информационный граф программы не изменяется, и в случае, если в результате разметки какой-либо дуги получается несколько новых ИГР, то они будут отличаться между собой только формулой у размечаемой дуги. Поэтому, для компактного отображения, эти ИГР можно объединить в один, у которого дуга будет размечена несколькими формулами одновременно. Отношение иерархии между формулами позволяет затем разделить компактное представление на исходные ИГР.

Проиллюстрируем вышесказанное на примере. На рис. 1.А приведена часть графа некоторой программы — четыре оператора соединены информационными связями. Узел 3 принимает входные данные с узлов 1 и 2, узел 4 принимает данные от узла 3. В начале, дуги в графе не размечены.

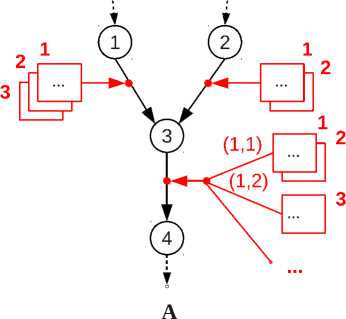
Рис. 1. Схематичное изображение преобразований информационного графа с разметкой. А — часть информационного графа программы, размеченная формулами. Узлы графа (обозначены кружками) представляют операторы программы, дуги — информационные связи, к дугам приписаны формулы (обозначены прямоугольниками), рядом с которыми указаны их номера, в круглых скобках указаны номера родительских формул. Б — эквивалентное преобразование «раскрытие параллельного списка». Параллельный список обозначен квадратными скобками, оператор интерпретации — линией, у которой кружок указывает функциональный вход

На первом шаге разметим дугу (1, 3). Если, при преобразовании графа, для оператора 1 применимо три аксиомы, то в результате преобразования получится три новых ИГР, которые компактно будут отображаться как исходный граф, у которого к дуге (1, 3) приписаны три формулы. На следующем шаге разметим дугу (2, 3). Число применимых аксиом для каждого из трех ИГР первого шага преобразований одинаково, так как операторы 1 и 2 независимы. Если при преобразовании трех ИГР для оператора 2 применимо две аксиомы, то в результате преобразования получится шесть новых графов. В компактном отображе- нии этих шести графов к дуге (2, 3) будут приписаны две формулы. Оператор 3 зависит от операторов 1 и 2, поэтому к каждому из шести полученных ИГР может быть применено разное количество аксиом. Пусть для первого ИГР это число соответствует двум (он распадется на два новых ИГР), для всех остальных — единице. В результате разметки получится семь графов, это число соответствует общему числу применимых аксиом и количеству формул, которые будут приписаны к дуге (3, 4). На рис. 1.А индексы (i,j) возле формул, помечающих дугу (3,4), обозначают номер i родительской формулы, помечающей дугу (1, 3), и номер j родительской формулы, помечающей дугу (2, 3).

• 1. 2. Изменение информационного графа

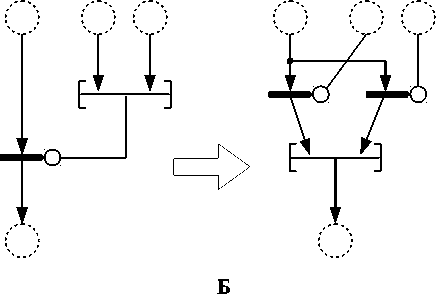
Второй тип преобразований изменяет информационный граф программы. Эквивалентное преобразование осуществляются по правилам эквивалентных преобразований операторов и связей языка Пифагор (описаны в [8, 10]). В результате преобразования получается один ИГР с измененным информационным графом. В качестве примера эквивалентного преобразования на рис. 1.Б приведено «раскрытие параллельного списка». Параллельный список позволяет явно указывать, что все поступающие в него операторы могут выполняться одновременно. В графе слева параллельный список из двух элементов поступает на функциональный вход оператора интерпретации. Оператор интерпретации имеет два входа для аргумента и функции, и осуществляет функциональное преобразование аргумента. В эквивалентном ему графе справа каждый элемент исходного параллельного списка поступает на функциональный вход своего оператора интерпретации, а уже результат их выполнения передается в параллельный список.

Другой вариант преобразований второго типа — расщепление, оно приводит к получению двух и более ИГР с измененными информационными графами. Расщепление можно использовать для упрощения доказательства, например, при разметке оператора выбора, если точно известны все варианты из которых делается выбор. Это позволяет упростить не только информационный граф программы, но и формулы разметки.

• 1. 3. Свертка

• 2.    Обобщенная структура системы поддержки формальной верификации

Третий тип преобразований — свертка программы. Свертка проводится над размеченной дугой (кроме входной и выходной дуг программы). Весь порожденный подграф с узлами, из которых достижимо начало рассматриваемой дуги (кроме входного аргумента), может быть заменен на новую переменную, а формула разметки данной дуги добавляется к предусловию исходного ИГР. При замене части кода на новую переменную программа сократится. Свертку можно проводить при частичной или полной разметке дуг графа программы. Если провести свертку над всеми размеченными дугами ИГР, полученному в результате ИГР будет соответствовать тройка Хоара. Назовем такую свертку полной . Когда в ИГР все дуги размечены, в результате полной свертки от всего графа остается одна переменная. Ее свойства описаны в предусловии, описывающем теперь свойства всех данных, передаваемых по дугам исходного графа. Она также является результатом работы программы. Такая программа называется пустой , и для определения ее корректности достаточно проверить следование постусловия из предусловия.

В результате всех рассмотренных преобразований ИГР ФПП программы можно сделать следующий вывод: весь процесс доказательства можно представить в виде дерева, корень которого — исходный ИГР, дочерние узлы получаются из родительских выполнением одного из преобразований 1)–3), а листья — полностью размеченные ИГР, над которыми проводится полная свертка и преобразование в формулы. Будем называть такое дерево — деревом доказательства или просто доказательством корректности программы.

На рис. 2 приведена общая схема системы для поддержки формальной верификации ФПП программ.

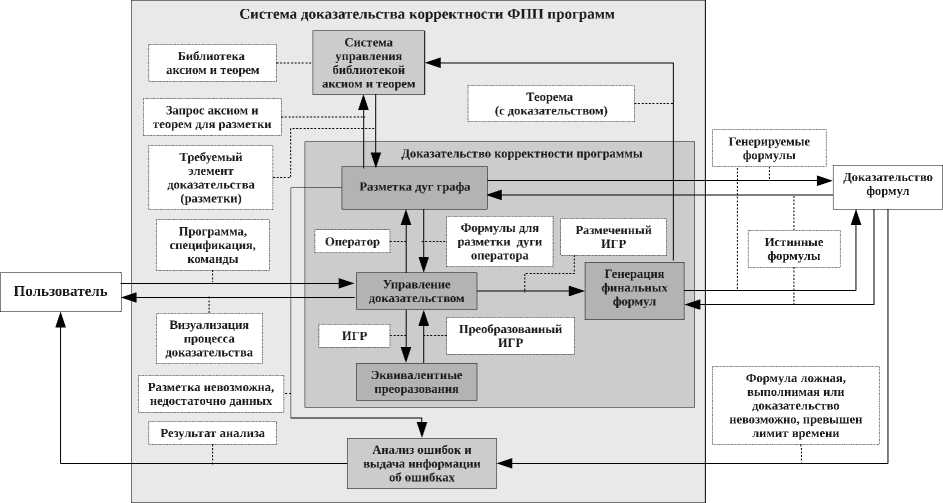
Рис. 2. Обобщенная структура системы поддержки формальной верификации

В системе можно выделить несколько модулей: «Модуль доказательства корректности программы», «Систему управления библиотекой аксиом и теорем» и «Модуль анализа ошибок и выдачи информации об ошибках». «Модуль доказательства формул» (верификатор формул) обособлен от системы, так как является сторонним и может не использоваться при доказательстве, а все его действия будет выполнять пользователь (самостоятельно или используя другой более удобный для него верификатор).

Принцип работы системы состоит в следующем. Пользователь передает системе программу на языке Пифагор и спецификацию программы на языке спецификации. «Модуль доказательства корректности программы» формирует исходный ИГР (которому соответствует исходная тройка Хоара) и начинает процесс доказательства, который заключается в разметке дуг графа программы формулами. Для этого используется информация об аксиомах и уже доказанных теоремах из «Библиотеки аксиом и теорем». «Модуль доказательства корректности программы» посылает запросы к «Системе управления библиотекой аксиом и теорем». В случае если запрашиваемая функция отсутствует в библиотеке, выдается ошиб- ка о невозможности разметки, которая обрабатывается «Модулем анализа ошибок». Если аксиомы (теоремы) для рассматриваемой функции присутствуют в библиотеке, то «Модуль доказательства корректности программы» проводит их отбор. Для каждой аксиомы (теоремы) из набора аксиом (теорем) для рассматриваемой функции формируется условие применимости данной аксиомы (теоремы) на языке спецификации. Это условие передается верификатору, и, если оно истинно или выполнимо, то аксиома (теорема) используется для разметки, иначе она отбрасывается. После того как все дуги в информационном графе программы будут размечены, проводится полная свертка. Тройки Хоара, соответствующие полученным ИГР, преобразуются в формулы (назовем их финальными формулами), которые передаются верификатору для проверки их истинности. Если все формулы истинны, то программа корректна, а ее исходная тройка Хоара — теорема. «Модуль доказательства корректности программы» передает полученную теорему (с доказательством) «Системе управления библиотекой аксиом и теорем», для сохранения в библиотеке. Если истинность формулы не доказана «Модуль анализа ошибок» определяет причину и сообщает об этом пользователю.

Рассмотрим работу «Модуля доказательства корректности программы» более детально (рис. 2). «Блок управления доказательством» является основным, он отвечает за взаимодействие с пользователем, принимает его данные, команды и визуализирует процесс доказательства. Данный блок формирует дерево доказательства. При получении ИГР, он ищет операторы с не размеченными дугами и передает их, в начале, «Блоку эквивалентных преобразований», а затем «Блоку разметки дуг» для получения формул разметки. После того как ИГР становится полностью размеченным, он передается «Блоку генерации финальных формул», который осуществляет полную свертку и генерирует множество финальных формул.

Рассмотренная система может работать в нескольких режимах:

• 1)    полностью ручной;

• 2)    частично автоматизированный;

• 3)    автоматизированный.

• 3.    Реализация системы

В первом случае пользователь использует только «Блок управления доказательством» и «Блок генерации финальных формул», а также «Модуль анализа ошибок». Он сам размечает дуги графа формулами и доказывает истинность финальной формулы. В частично автоматизированном режиме не задействован только «Модуль доказательства формул», и пользователь сам указывает, истинна, ложна или выполнима сгенерированная формула. В автоматизированном режиме задействованы все модули.

В соответствии с рассмотренной обобщенной структурой разработана программа, обеспечивающая поддержку формальной верификации ФПП программ, которая позволяет строить дерево доказательства программы на языке Пифагор.

Пользователю предоставляется графический интерфейс для редактирования дерева доказательства. В качестве входных данных программа принимает формулы разметки в текстовом виде, а код программы — в виде текстового представления реверсивного информационного графа (РИГ) программы [11, 12], который описывает существующие в программе зависимости по данным (отличается от информационного графа тем, что дуги ориентиро- ванны в противоположном направлении). Также можно загрузить ранее созданный ИГР или дерево доказательства.

Главное окно программы (рис. 3) представляет собой редактор дерева доказательства. В левой его части располагается редактор узлов дерева, а в правой — редактор ИГР, в котором отображается текущий узел дерева. Редактор узлов дерева доказательства позволяет вставлять новые и уже существующие ИГР, копировать, удалять текущие ИГР и вставлять скопированный ИГР, как дочерний к текущему.

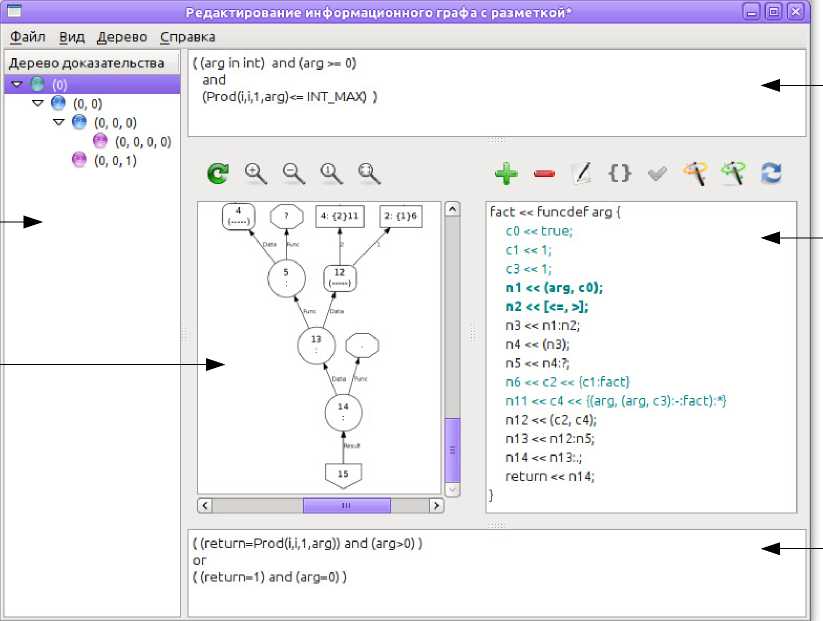
Рис. 3. Главное окно средства инструментальной поддержки формальной верификации функционально-потоковых параллельны программ; 1 — редактор узлов дерева доказательства, 2 — поле ввода предусловия, 3 — поле ввода постусловия, 4 — редактируемый код программы, 5 — графическое представление реверсивного информационного графа программы

Редактор ИГР в своей верхней и нижней части содержит поля для ввода предусловия и постусловия программы соответственно, в левой части отображается графическое представление РИГ, а в правой — редактируемый код программы. Для получения графического представления РИГ используется сторонняя программа GraphViz, которой передается файл формата dot. Редактор кода представлен панелью инструментов и текстом программы, разбитым на строки, где каждая строка соответствует одному узлу РИГ программы. РИГ имеет текстовый формат и создается по программе. Такой РИГ имеет правильный порядок вызовов функций, то есть функция будет вызвана только после того как определена. По такому текстовому представлению однозначно восстанавливается код программы.

Редактор кода программы позволяет добавлять, удалять и редактировать узлы РИГ. При этом, ограничения не позволят пользователю обратиться к оператору до его определе- ния. Присутствует возможность редактировать задержанные списки. Оператор группировки в задержанный список (или, кратко, задержанный список) содержит подграф программы. Операторы, находящиеся в задержанном списке, не могут выполняться даже при наличии всех аргументов. Их активизация возможна только при снятии задержки, когда ограниченный подграф становится частью всего вычисляемого графа [7, 8]. Редактор кода имеет возможность любой оператор поместить в задержанный список, при этом в задержанный список помещаются все операторы, которые использует данный оператор. Задержанный список рассматривается как константа, поэтому редактирование операторов задержанного списка возможно только после снятия задержки.

Пользователь может вызвать функцию автоматической разметки дуг, либо использовать редактор ИГР для ручной разметки. В редакторе используется компактное отображение получаемых ИГР. Если дуга еще не была размечена, то производится проверка готовности разметки на всех входных дугах. Если хотя бы на одной из входной дуг любого из рассматриваемых в компактном представлении графов разметка отсутствует, то выдается соответствующее сообщение о невозможности разметки текущей дуги. Если все входные дуги размечены, то появляется окно (рис. 4) с иерархией формул дуги текущего узла, где все формулы разделены на группы, соответствующие различным комбинациям формул родительских узлов. Слева представлен список индексов родительских формул, а справа на вкладках размещаются формулы разметки текущей дуги. Пользователь может добавлять новые формулы, что автоматически изменяет индексы всех дочерних узлов (если они уже размечены), у которых появляется необходимое количество пустых вкладок для новых формул. При удалении формул, удаляются все формулы потомков, дочерние по отношению к текущей формуле, и изменяются индексы оставшихся формул.

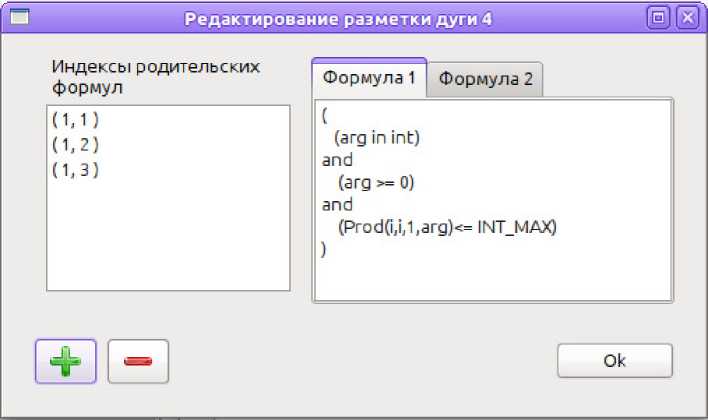
Рис. 4. Окно редактирования иерархии формул размечаемой дуги

Пользователю также доступны следующие функции: автопреобразование, авторазметка ИГР и генерация финальных формул.

Автопреобразование текущего ИГР (автоматическое выполнение эквивалентных преобразований) выполняется в случае, если он является листом дерева доказательства, иначе его дочернее поддерево должно быть удалено. Кроме того, преобразуются только готовые операторы, то есть те операторы у которых размечены все входные дуги, а выходная дуга еще не размечена. У всех готовых операторов текущего графа проверяется возможность применения эквивалентного преобразования. Если к ИГР можно применить эквивалентное преобразование, то новый полученный ИГР становится дочерним к исходному.

Функция автоматической разметки применяется к текущему графу. В начале для него проводятся эквивалентные преобразования, затем находится готовый оператор, для того чтобы провести разметку его выходной дуги. Если оператор является списком, то выходная дуга размечается константой true, если это оператор интерпретации, то для функции с его функционального входа, запрашивается список аксиом (для встроенных функций) или теорем (для функций пользователя) в библиотеке аксиом и теорем. Если функция присутствует в библиотеке, то для каждой ее аксиомы или теоремы формируется условие применимости, истинность или выполнимость которого требуется определить пользователю. Аксиомы или теоремы, для которых условие тождественно ложно, отбрасываются, а все оставшиеся используются для разметки дуги рассматриваемого оператора интерпретации несколькими формулами. Далее осуществляется поиск другого готового оператора.

Если все дуги текущего информационного графа размечены, то к нему может быть применена полная свертка, и полученные в результате тройки Хоара с пустой программой можно преобразовать в формулы. Это реализуется функцией генерации финальных формул.

Таким образом, на данный момент реализован ручной и частично автоматизированный режим работы системы.

Заключение

В работе рассмотрены основные преобразования, которые претерпевает информационный граф с разметкой при построении доказательства корректности программы. Разработаны основные концепции архитектуры инструментального средства для поддержки формальной верификации ФПП программ. Задача реализации рассмотренной системы частично решена. В настоящее время ведется работа над расширением функциональности частично автоматизированного и реализацией автоматизированного режима работы системы.