Интеграция алгебраического и геометрического методов в решении задач

Современный этап реформирования общего среднего образования предполагает новый методологический подход к его организации и содержанию, главная идея которого заключается в том. чтобы интегрировать учебный материал, уплотнить его, установить зависимости и межпредметные связи.

Интеграция знаний вызвана прежде всего практикой. В эпоху научно-технической революции большинство практических задач требует для своего решения умения применять знания в комплексе, т. е. привлекать, объединять, суммировать большое число разнообразных компонентов научного знания, относящихся иногда к очень отдаленным друг от друга областям науки.

От того, насколько быстрым и эффективным будет этот перенос знаний, зависит в конечном счете успех в решении поставленной жизнью задачи. При этом необходимо заметить, что логика, которой руководствуется специалист в своей исполнительской или творческой деятельности, отличается от логики линейного и упорядоченного накопления знаний в школе (или вузе).

Обучение переносу знаний, умению использовать их в комплексе - это проблема интеграции. Процесс интеграции в обучении понимают как «взаимовлияние, взаимопроникновение и взаимосвязь содержания различных учебных дисциплин» (Н.С. Антонов).

В области обучения математике в средней школе мы приходим к необходимости

интеграции алгебры и геометрии, одной из причин которой является существующая тенденция к уменьшению числа учебных часов, отводимых на изучение этих дисциплин. Полная интеграция алгебры и геометрии невозможна в силу разных концепций построения данных курсов: курс алгебры строится на аналитико-алгоритмической основе, а курс геометрии - на образносинтетической. Однако можно устанавливать содержательные связи между этими курсами посредством интеграции их методов.

Обучение математике - это в первую очередь решение задач. В ходе самостоятельных размышлений учащихся над задачами происходят развитие мышления и формирование способности к математической деятельности. Есть опасность, что при введении централизованного тестирования для абитуриентов в целях подготовки к этому экзамену будет наблюдаться «натаскивание» учащихся на решении большого количества однотипных задач, что приведет в итоге к снижению развивающей функции обучения математике. Мы должны заботиться сегодня не только о том, чтобы абитуриенты успешно прошли тестирование, но и о том, чтобы они смогли успешно учиться в вузе, т. е. имели определенный уровень математической культуры.

Математическая культура предполагает наличие широкого кругозора, умения по малейшим незаметным признакам находить аналогию с другими (иногда очень далекими) областями математики, умения переформулировать задачу на другой язык, находить новые модели задачи, более простые, более наглядные.

Конечно, нужно уметь считать, выполнять тождественные преобразования, знать формуты и уметь применять их, но все это не может заменить решение задач, которые заставляют думать, сопоставлять различные методы, искать другие формулировки, находить связи с другими разделами математики. Именно такие задачи и красота их решений воспитывают хороший вкус и математическую культуру. По словам В.Г. Болтянского, «красота математического рассуждения складывается из наглядности и неожиданности». Поэтому большое значение в решении задач имеет интеграция алгебраического и геометри- ческого методов в силу того, что геометрический метод неразрывно связан с геометрическими представлениями, с геометрической интуицией, с воображением.

С психологической точки зрения интеграция двух названных методов в решении задач ведет к гармоничному развитию полушарий головного мозга, что является одной из главных целей обучения математике на современном этапе.

Взаимосвязь знаний из алгебры, геометрии и даже физики можно устанавливать при решении обычных школьных задач. Приведем некоторые примеры.

Задача 1. Поезд должен был пройти 54 км. Пройдя 14 км, он был задержан у семафора на 8 мин. Увеличив скорость после этого на 10 км/ч, он прибыл на место назначения по расписанию. Определить первоначальную скорость поезда.

• I.    Алгебраический метод решения этой задачи приводит к уравнению

40 40 _ 2 х х + 10 15 ’ где х - первоначальная скорость поезда (км/ч).

• II.    Решим эту задачу, используя геометрические представления, в частности двумерную диаграмму. Так как в задаче рассматривается равномерное движение, то пройденный поездом путь можно представить в виде произведения скорости и времени движения. Пусть сторона АВ прямоугольника ABCD изображает первоначальную скорость поезда (км/ч), а сторона AD - время его движения (ч) (рис. 1).

  

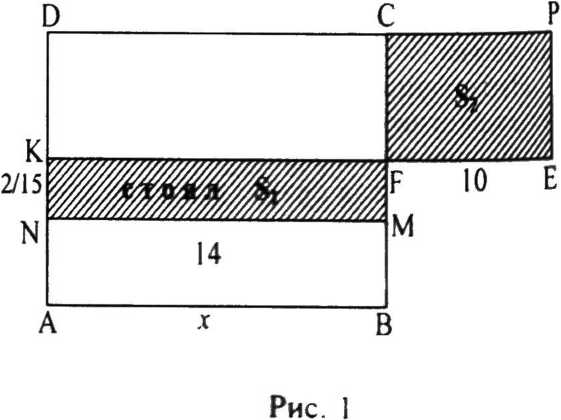
Тогда площадь прямоугольника ABCD определяет весь путь, который должен пройти поезд (км).

^ABCD ⁼ ^ ‘ ^^ = 54.

Пусть АВ = х, S_ABMN = 14, a S, определяет путь, который прошел бы поезд за время стоянки. За счет увеличения скорости на 10 км/ч поезд нагнал потерянное время, поэтому S₍ = S₂, т. е.

2 _1А 40 х 200

— х = Ю--ипи — =----

15 x + IO^IS х + Ю

После преобразований имеем х2 + Юх-3000 = 0, откуда х( = 50, х, = -60. Второй корень не удовлетворяет условию задачи, поэтому получаем ответ: первоначальная скорость поезда была 50 км/ч.

Как видим, данный метод решения представляет собой интеграцию двух методов: геометрического (используются геометрические представления, понятие и свойства площади, равновеликость) и алгебраического (используются уравнения, тождественные преобразования выражений и т.п.).

Задача 2. Два всадника выезжают одновременно из пунктов А и В навстречу друг другу. Один прибывает в пункт В через 12 мин, а другой в пункт А через 27 мин после встречи. За сколько минут проехал каждый всадник свой путь?

• I.    Алгебраический метод решения приводит к уравнению

I I I --1--= —. / +12 / + 27 t где t - время движения всадников до встречи (ч).

• II.    Решим задачу, используя графикогеометрический метод.

Рассмотрим две системы координат tAS и t'BS'. At и Bt' - оси времени с одинаковыми масштабами, AS и BS' -оси пройденного пути. Отрезок АВ изображает расстояние между пунктами А и В. Так как в задаче рассматривается равномерное движение, то геометрическая модель задачи имеет вид, представленный на рис. 2.

Используя чертеж и один из признаков подобия треугольников, получаем:

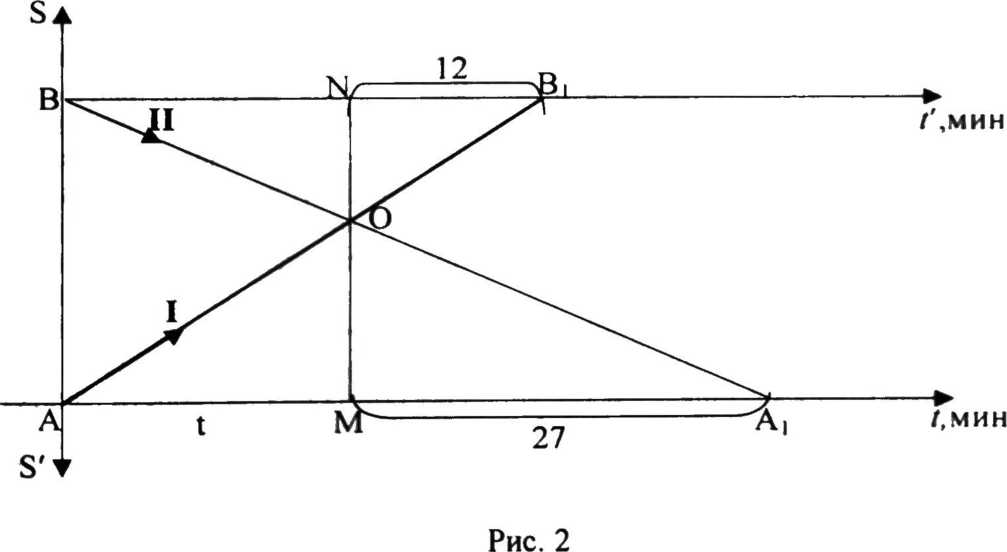
Из (I) и (2) следует, что — -

ДАМО ~ ДВ^О, отсюда следует:

t_ _ МО 12 "  ON ’

ДА]МО ~ ДВМО, отсюда следует:

27 - МО t ~ ON

(I)

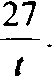
или

t2 = 27 12, тогда t =+18.

Отрицательное значение корня не удовлетворяет условию задачи, поэтому t = 18 мин. Окончательный ответ:

I, = ВВ, = 30 мин, ^ = АА, = 45 мин.

В данном примере геометрическая модель задачи помогает наглядно представить ее содержание и задействовать в процессе решения знания из трех дисциплин: алгебры, геометрии, физики.

Интеграция алгебраического и геометрического методов в решении задач развивает у учащихся творческое мышление, формирует у них понимание единства математической науки и готовит к решению задач, возникающих в практической деятельности.

ИНТЕГРАЦИЯ МЕТОДОВ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

Интеграция методов при решении задач играет важную роль в профессиональной подготовке будущих учителей математики. Во-первых, решение задач различными методами способствует углублению знаний, их систематизации и обобщению, позволяет установить новые связи и отношения между ними. Поиск нового способа решения задачи требует от студента хорошего знания теории, глубокого, разностороннего осмысления заданной ситуации, стимулирует учебно-познавательную активность обучаемых. Во-вторых, интеграция геометрических методов решения задач способствует повышению интереса к предмету. Не секрет, что решение геометрических задач в силу их эвристической природы вызывает большие трудности не только у учащихся, но и у студентов по сравнению с решением задач алгебры и анализа. От степени заинтересованности обучаемых во многом зависят характер их внимания на занятиях, активность, творческий подъем.

Одним из действенных стимулов учения студенческой молодежи является профессиональный мотив. Он определяется сочетанием интереса к профессии с интересом к учебным предметам. Решение задач различными методами позволяет продемонстрировать связь геометрии, изучаемой в педвузе, с элементарной геометрией, взглянуть на школьный курс с точки зрения высшей математики.

Часто в обучении математике в школе различные методы решения геометрических задач иллюстрируются на разных задачах, которые подбираются специально как имеющие наиболее эффективные реше ния данными методами. Поэтому в сознании учащихся метод невольно связывается с задачей, а его самостоятельная значимость как бы приглушается. Но когда одна и та же задача решается разными методами, их отличительные черты, сильные и слабые стороны выступают наиболее ярко.

Интеграция методов при решении геометрических задач помогает студенту тем, что, решая одну и ту же задачу различными методами, можно лучше понять специфику того или иного метода, его преимущества и недостатки в зависимости от со-держания задачи.

Систематическая, планомерная и настойчивая работа по формированию навыков применения различных методов решения задач способствует развитию у студентов приемов логического поиска, развивает их творческие способности. Общепризнанно, что подлинно творческая деятельность начинается там, где ведется самостоятельный поиск новых решений, намечаются новые, более совершенные, оригинальные его направления, рациональные способы решения теоретических и практических задач. Кроме того, интеграция методов решения задач способствует развитию чувства математической красоты, гармонии чисел и форм, геометрической выразительности, т.е. является одним из средств эстетического воспитания.

Приведем примеры решения таких задач.

Задача 1. На сторонах АВ и АС треугольника АВС взяты точки М и N, такие,

AM CN  1

что —— - — - - (рис. 1). Отрезки BN Md  NA  Л