Интеграция методов решения геометрических задан

Интеграция методов при решении задач играет важную роль в профессиональной подготовке будущих учителей математики. Во-первых, решение задач различными методами способствует углублению знаний, их систематизации и обобщению, позволяет установить новые связи и отношения между ними. Поиск нового способа решения задачи требует от студента хорошего знания теории, глубокого, разностороннего осмысления заданной ситуации, стимулирует учебно-познавательную активность обучаемых. Во-вторых, интеграция геометрических методов решения задач способствует повышению интереса к предмету. Не секрет, что решение геометрических задач в силу их эвристической природы вызывает большие трудности не только у учащихся, но и у студентов по сравнению с решением задач алгебры и анализа. От степени заинтересованности обучаемых во многом зависят характер их внимания на занятиях, активность, творческий подъем.

Одним из действенных стимулов учения студенческой молодежи является профессиональный мотив. Он определяется сочетанием интереса к профессии с интересом к учебным предметам. Решение задач различными методами позволяет продемонстрировать связь геометрии, изучаемой в педвузе, с элементарной геометрией, взглянуть на школьный курс с точки зрения высшей математики.

Часто в обучении математике в школе различные методы решения геометрических задач иллюстрируются на разных задачах, которые подбираются специально как имеющие наиболее эффективные реше ния данными методами. Поэтому в сознании учащихся метод невольно связывается с задачей, а его самостоятельная значимость как бы приглушается. Но когда одна и та же задача решается разными методами, их отличительные черты, сильные и слабые стороны выступают наиболее ярко.

Интеграция методов при решении геометрических задач помогает студенту тем, что, решая одну и ту же задачу различными методами, можно лучше понять специфику того или иного метода, его преимущества и недостатки в зависимости от со-держания задачи.

Систематическая, планомерная и настойчивая работа по формированию навыков применения различных методов решения задач способствует развитию у студентов приемов логического поиска, развивает их творческие способности. Общепризнанно, что подлинно творческая деятельность начинается там, где ведется самостоятельный поиск новых решений, намечаются новые, более совершенные, оригинальные его направления, рациональные способы решения теоретических и практических задач. Кроме того, интеграция методов решения задач способствует развитию чувства математической красоты, гармонии чисел и форм, геометрической выразительности, т.е. является одним из средств эстетического воспитания.

Приведем примеры решения таких задач.

Задача 1. На сторонах АВ и АС треугольника АВС взяты точки М и N, такие,

AM CN  1

что —— - — - - (рис. 1). Отрезки BN Md  NA  Л

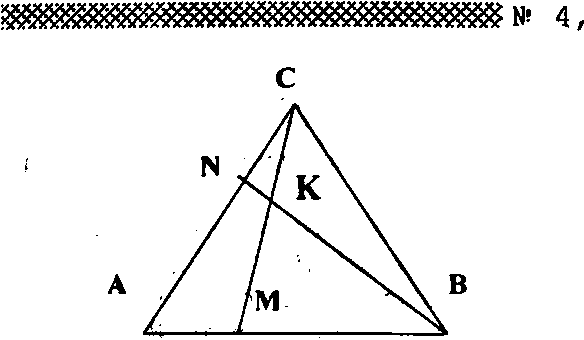
Рис. 1

2001 Й^Ж^^

Решая систему уравнений, находим х = 6,у=-

Второй способ (координатный метод). Точку А треугольника АВС примем за начало аффинной системы координат, направленные прямые АС и АВ - за оси координат.

Пусть вершины В и С треугольника АВС имеют координаты В(3; 0), С(0; 3).

и СМ пересекаются в точке К. Найдите ВК СК отношения отрезков ~— и TZ">

KN КМ

Эта задача может быть решена тремя способами.

Первый способ (векторный метод).

„ ВК СК

Обозначим ---= X И --- = V. ДЛЯ того

KN КМ чтобы вычислить х и у, выразим вектор ЛК двумя способами: через векторы АВ и АС.

По формуле деления отрезка в данном

• —— АВ а- х AN отношении имеем АК = -------- и

• 1 + Х

_т AM CN 1            _К1

• 1    ак как ---= = —. то точки М и N

ВМ NA 2

имеют координаты М(1; 0), N(0; 2). Координаты точки К найдем, решая систему уравнений

2х + Зу-6 = 0.

Зх + у - 3 = 0.

Получаем, что точка К имеет коорди- f3. 12)

наты К zi ZT г

Пусть точка К делит отрезок BN в от-

ВК . ц „     , ношении ---= к. Найдем к, используя

KN формулу деления отрезка в данном отно-

ВК шении. Получаем к = 6, те. ---= 6.

KN

1 + ^

Согласно условию задачи АМ = - А В,

_К               СК 3

Аналогично находим = —.

КМ 4

Третий способ. Применим теорему

Менелая к М.СМ и секущей ВК. Тогда

AN=-AC.

АВ+ ^хАС

Следовательно,

_         _ ^АВ+АС

АК =----^---- и АК = 3

1 + х

В силу единственности разложения вектора по двум неколлинеарным векторам получим

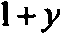
	СК км	МВ	AN	= 1.
		ВА	NC
Та it	как	МВ _	2	AN	= 2,	ТО
1 Cllx		В А	3’	NC

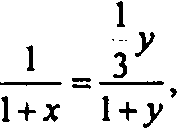
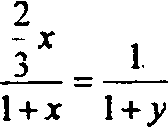
с/: _ 3

КМ™ 4

Аналогично, применив теорему Менелая к MBN и секущей СК, находим

ВК 1 1 , -----= 1 откуда

KN 3 2

^=6.

KN ______

«■^ ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ ^^^^

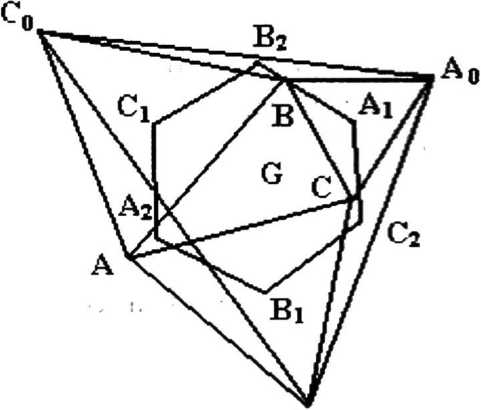
Задача 2. На сторонах ВС, СА и АВ треугольника АВС построены в его плоскости равносторонние одинаково ориентированные треугольники ВСА0, САВ0, АВС0. Докажите, что центры Ар Вр С] этих треугольников и центроиды А2, В„ С2 треугольников В0С0А, С0А0В, А0В0‘С являются вершинами правильного шестиугольника, центр которого совпадает с центром G данного треугольника (рис. 2).

Во

Рис. 2

Первый способ (векторной метод). Пусть О - некоторая точка. Известно, что если G - центроид треугольника АВС, то

ОС = — \ОА + ОВ + ОС . Следователь-3V              ’ но,

О Ах ^ЦоА^ОВ-vOC 3^V

ОА з =-(ОД+ 05 о + ОСо1

Обозначим через Р середину отрезка А]А,. Тогда ор=Цоа.+оаЗ=

— — (оА + ОВ + ОС + OAq + OB_Q + OCq j.

или OP = - (од + ОС 2V где Go - центроид треугольника А0В0С0.

Отсюда видно, что если точки G и Go совпадают, то совпадают и все три точки Р, G и Go.

Для векторов, соответствующих серединам отрезков В,В, и С, С,, получим то же самое выражение, те. середины этих отрезков совпадают с точкой Р. Таким образом, точка Р есть центр симметрии шестиугольника А^^А^С, и поэтому противоположные стороны шестиугольника равны и параллельны.

Второй способ (метод геометрических преобразований). Поворот А_р⁶⁰' отображает точки А и А_о соответственно на точки В_о и В, а отрезок АА₀ - на отрезок В₀В. Следовательно, АА_й = В _йВ и угол между лучами АА₀ и В₀В равен углу поворота, те. угол между векторами АА о и В₀В равен 60°.

Пусть К, L, М, N - середины отрезков А0В, АВ, АВ0 и А0В0. Тогда отрезки KL и MN являются средними линиями треуголь-ников АА0В и АА0В0, поэтому

KL = МН = -АА^. Аналогично

LM = KN = — BBn. Следовательно, че-2 ° тырехугольник KLMN является параллелограммом. А так как АА^ = ВВ0, то KL = LM и KLMN - ромб, причем угол LMN равен углу между векторами АА о и В0В и составляет 60°

Гомотетия Нр отображает точки L, М, N соответственно на точки G, В_р С,. Поскольку треугольник LMN - равносторонний, то треугольник GB,C₂ также равносторонний.

Таким же образом докажем, что треугольники GC,Ap GA,В, и др. являются равносторонними, и, следовательно, получаем правильный шестиугольник A,B, С ,A,Bt С, с центром G.

«■^^        4,

Задача 3. Декажите, что медианы треугольника пересекаются в одной точ-_ ке и делятся в отношении 2:1, считая от вершины.

С этой задачей учащиеся встречаются в школьном курсе геометрии, где для ее решения применяется подобие. Рассмотрим другие методы решения этой задачи.

Доказательство. Эта задача имеет два способа решения векторным методом.

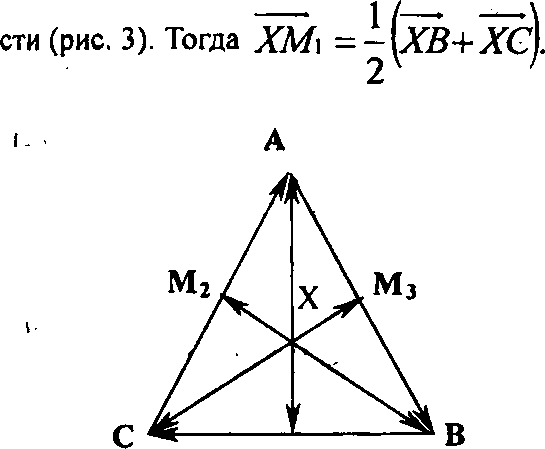
Первый способ. Пусть М_р М₂, М₃ -середины сторон ВС, АС, АВ треугольника ABC, X - произвольная точка плоско-

М,

Рис. 3

Пусть X, - точка, которая делит медиану AMj в отношении AXf: Х^, = 2:1. Тогда по формуле деления отрезка в данном отношении имеем

XX \ = -ХА+ — ХМ\ +-Х4 + 3      3        3

• 2    / 1 /— —\\ 1 /— '— —. +--АД + ZC =-\ХА а- ХВ а- ХС

3\2V          3V

Аналогично, если X, и X. - точки, которые делят медианы ВМ, и^СМ. в отношении ВХ,: Х2М2 = СХ3: Х3М3 = 2 : 1, то,

XX i =№ = -1ХА+ХВ+ХС,

т.е.

точки Хр Х2, Х3 совпадают.

Второй способ. В треугольнике АВС (рис. 4)

2ММ\=МВ+МС. 0)

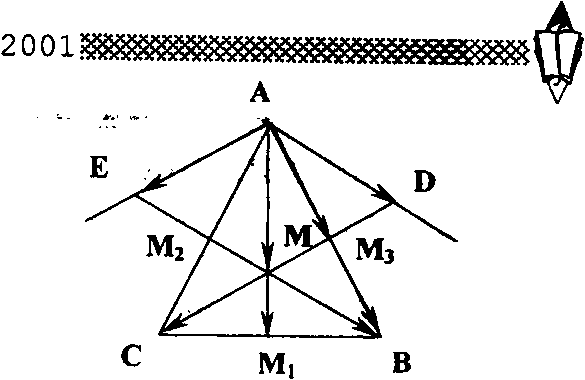
Рис. 4

Разложим вектор АМ по векторам МВ и МС : АМ = аМВ*р МС.

Сделаем параллельный перенос векторов МВ и МС на вектор МА.

Получим параллелограмм ADME, АМ = AD + АЕ.

ы AD АМз *

МВ М3В

ГИЧНО Р = 1.

Таким образом, АМ = МВ + МС. (2)

Сравнивая (1) и (2), получаем

АМ = 2ММ\, что доказывает утвержде ние задачи.

Наиболее рациональным является решение этой задачи с помощью теоремы Чевы и теоремы о пропорциональных отрезках.

Третий способ. Пусть АМр ВМ„ СМ₃ - медианы треугольника АВС. По тё-

ЛЛ/₃ ВМ. СМ, .

ореме Чевы------ = 1 •

Р       М3В МХС МгА

Следовательно, медианы АМР ВМ,, СМ, пересекаются в одной точке.

Применяя теорему о пропорциональных отрезках, получаем

АХ

ХМх

АМ₃ Г ВМ_Х

М3В\МХС

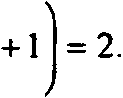
ВХ сх

Аналогично „ — = 2, —— = 2, т.е.

каждая медиана делится точкой X в отношении 2:1, считая от вершины.