Интегральная модель дробного томсоновского автогенератора

В последнее время под влиянием возросшего интереса к естественнонаучным приложениям [1] теории дробного интегро-дифференцирования формируется новый раздел динамики – дробная динамика или в англоязычном варианте – фрактальная динамика (fractional dynamics) [2]. Он охватывает исследования систем с интегро-дифференциальными уравнениями движения дробного порядка. Среди них одно из центральных мест, несомненно, принадлежит автоколебательным системам с фрактальными связями – активным фрактальным осцилляторам.

В работе [3] на основе схемы радиоэлектронного автогенератора с дробной цепью возбуждения резонансного контура введена в рассмотрение дифференциальная модель активного фрактального осциллятора (АФО). В [4] предложен алгоритм численного интегрирования дифференциального уравнения движения осциллятора. В настоящем сообщении автоколебания в АФО предлагается исследовать методами численного решения интегрального уравнения движения динамической системы.

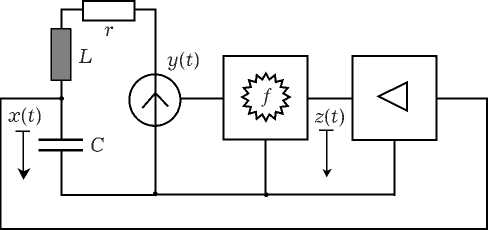
Рис. 1. Эквивалентная схема автогенератора

1.    Интегральное уравнение движения АФО

Эквивалентная схема автогенератора томсоновского типа с дробной цепью возбуждения контура и нелинейным усилителем представлена на рис. 1.

Элементы схемы моделируются уравнениями d2x d?+

to, dx 22

d_ _+Юо x _{= Юо} y ,

y = tooaD?z ,(2)

z = K g (x).(3)

Здесь первое уравнение описывает колебательный контур с собственной частотой to o и добротностью Q . Второе уравнение с производной Капуто D t относится к цепи возбуждения дробного порядка а, третье — к усилителю с малосигнальным коэффициентом усиления к и нелинейной передаточной функцией g ( x ).

Дифференциальная модель АФО в форме уравнений (1)–(3) методом работы [5] приведена к интегральному уравнению Вольтерра второго рода t

x ( t ) = ко^{2 а} J h ( t - т) D ^а g ( x ( t ) ) d т + X ( t )        (4)

с ядром h ( t - т) в виде импульсной характеристики осциллятора (1):

h ( t ) = — exp - -^{to o}- 1 sin(to i t )9( t ), to 1      ( 2 Q )

где toi = too\1 - 1/ 4Q2 , 0(t) — функция Хевисай- да. Функция времени X(t) в уравнении (4) описы-

вает свободные колебания в контуре, зависящие от начальных условий.

2.    Алгоритм и результаты численного моделирования

При численном решении интегрального уравнения (4) перейдем в нем к безразмерному времени t ^ to o t , сохранив для него прежнее обозначение. Кроме того, предполагая высокую ( Q > 10 ) добротность контура, будем считать К> 1 = to 0 - Тогда уравнение и его ядро (импульсная характеристика) примут вид

t

x ( t ) = k J h ( t - т) D “ g ( x ( t ) ) d т + X ( t ),             (5)

h ( t ) = exp

Производную Капуто D “ g ( x ( t ) ) на дискретной временной сетке t n = n А аппроксимируем конечными разностями:

n

^D “ g ( ^{x (} tn, ) ) = ^ p n - k ( g ( ^{x (} t k ) ) - g ( ^{x (} t k — 1 ) ) ) , ⁽⁷⁾ k = 1

где p nk

А “ Г(2 - a)

[ ( n - k + 1 ) ¹ “

- ( n - k ) 1 “ j,

а Г( z ) — гамма-функция. Порядок данной аппроксимации зависит от величины a: при a ^ 1 формула дифференцирования (7) имеет погрешность O ( А ) , а при a ^ 0 она является точной.

Для представления интеграла в правой части уравнения (5) воспользуемся квадратурной формулой трапеций. С учетом того, что h(0) = 0 и Dt“g (x(0)) = 0, конечно-разностное представление интегрального уравнения (5) принимает вид n-1 m xn = k       p m -kh(tn - tm) x m=l k=1                                 (8)

x( g (xk)- g (xk-i)) + Xn, где Xn – отсчеты свободных колебаний с начальным состоянием x(0) = 0, x‘(0) ^ 0:

X n = x '(0) exp

- t n sin( t ). 2 Q J     n

Соотношение (8) является рекуррентной формулой и позволяет последовательно рассчитывать значения отсчетов x_n автоколебаний на дискретной временной сетке начиная с n = 2 при начальных условиях x ₀ = 0 и x i = x '(0)А. Результаты моделирования процесса установления автоколебаний в АФО по алгоритму (8) иллю-

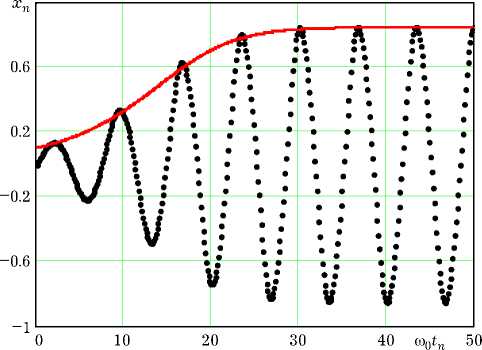
Рис. 2. Процесс установления автоколебаний

стрируются рис. 2. На нем точками отмечена последовательность отсчетов x_n , рассчитанная при начальном условии x ‘(0) = 0.1 с шагом А = 0.125 для осциллятора с параметрами Q = 10, к = 0.5 и a = 0.5.

Непрерывной линией на рис. 2 показан график временной зависимости амплитуды первой гармоники автоколебаний, полученный в результате решения приведенного в [3] укороченного уравнения

---=--1 1 -к Q (1 - A ²)sin |aⁿ||.            (9) dt     2 Q (                 I 2 J J

Из рис. 2 видно, что численные и приближенные аналитические результаты моделирования автоколебаний находятся в хорошем количественном соответствии. Наличие незначительного расхождения результатов объясняется тем, что аналитическое решение получено методом гармонической линеаризации и не учитывает высших гармоник автоколебаний, присутствующих в численном решении (8). С ростом параметра превышения порога генерации к Q степень расхождения численных и аналитических результатов увеличивается. Поэтому для моделирования существенно нелинейных режимов автоколебаний (к Q > 10) следует пользоваться численным решением.

3.    Усечение импульсной характеристики

Вычислительную эффективность алгоритма (8) можно повысить, если вместо полной импульсной характеристики (6) в уравнении (5) использовать усеченную во времени функцию вида h (t) = exp

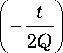
sin( t ) [ 0( t ) -0( t - T h ) ]

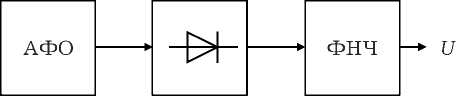
Рис. 3. Схема численного эксперимента

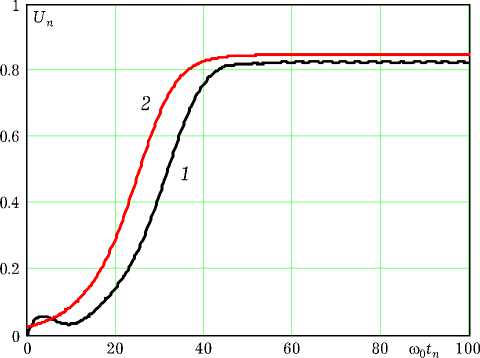
Рис. 4. Огибающая автоколебаний по результатам численного эксперимента

• т. е. импульсную характеристику конечной длительности T_h . В этом случае для вычисления значений Х п при n >  M = T h / А вместо формулы (8) следует использовать формулу

n-1 m xn = К ^< ^^ Рm—kh(tn - tm) X m=n - M+1 k=1 ( )

^X ( g ( x k ) ^- g ( x k - 1 ) ) .

Дать теоретическую оценку погрешности вычислений с усеченной импульсной характеристикой не представляется возможным. Поэтому оценим погрешность на основании результатов численного эксперимента, в котором сигнал АФО подвергнем преобразованию по схеме, приведенной на рис. 3.

После двухполупериодного детектирования сигнала x_n из (8) и последующей низкочастотной фильтрации результата (использован фильтр Баттерворта четвертого порядка с частотой среза to c = 0.4to g ) получен сигнал U n , показанный на рис. 4 линией 1. Линия 2 отображает решение укороченного уравнения (9) для амплитуды первой гармоники автоколебаний.

Как следует из рис. 4 с учетом начальной реакции фильтра и группового запаздывания можно утверждать, что в эксперименте надежно выделяется огибающая автоколебаний. На следующих этапах эксперимента эта огибающая сравнивается с огибающими U_n ^{( M )} автоколебаний, рассчитанных по усеченной импульсной характеристике. На рис. 5 представлен результат такого

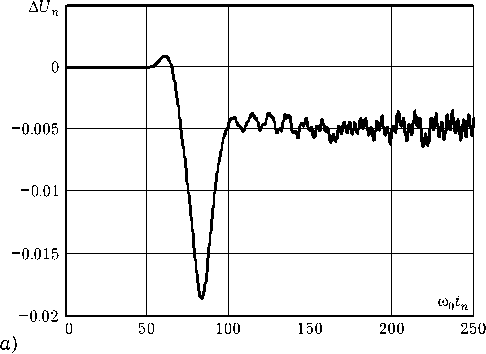
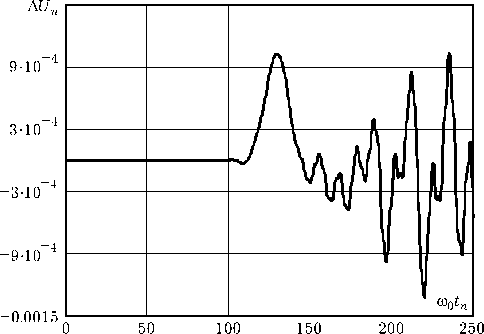
б)

Рис. 5. Погрешность усечения импульсной характеристики сравнения — разность А Un = Un - UM). Разность на рис. 5, а соответствует усечению импульсной характеристики на уровне ее огибающей 0.1 от максимального значения, на рис. 5, б – на уровне 0.01.

Погрешность в 1–2 % в первом случае и 0.1 % во втором указывает на применимость процедуры усечения импульсной характеристики при практических вычислениях.

Заключение

Предложенные здесь численный алгоритм расширяет возможности математического моделирования динамических систем с дробными производными и позволяет устанавливать пределы применимости приближенных аналитических методов.