Интегральное уравнение регулирования стока

Ставится следующая задача. Пусть задан некоторый объем β . Этот объем случайным образом заполняется объемами k_i .

Функция плотности поступления объема к _i в объем β задается в виде q ( x ) .

В момент поступления объема k_i из объема β изымается некоторый заданный объем α , причем если объем k_i – α > β , то значение заполнения объема β до отметки x принимается равным β ; если k_i – α < 0, то х = 0 .

Требуется определить вероятность заполнения объема β до заданной отметки х в бесконечной перспективе.

Обозначим ϕ (х / y ) – условную функцию вероятности заполнения объема β до отметки х в i -й момент при условии, что в ( i - 1 )-й момент отметка была равна y . Через ϕ ( õ ) обозначим искомую функцию, определяющую вероятность наполнения данного объема до отметки х .

Запишем формулу полной вероятности для этих двух функций:

β

ϕ (х) = - ( s ) ∫ ϕ ( x / y ) d ϕ ( y ) .                            (1)

Интеграл понимается в смысле Стилтьеса.

Переходя к интегралу Римана, получим:

β

ϕ (х) = А(х + α ) + ∫ ϕ ( y ) g ( x - y + α ) dy .                   (2)

Уравнение (2) аналитически разрешимо при β < α . В противном случае оно имеет разрывное ядро и становится устранимо сингулярным.

В инженерно-гидрологических расчетах наибольшее распространение получили кривые распределения К. Пирсона III типа.

Такая плотность распределения имеет вид:

γ

q ( x ) = ^γ k ^{γ - 1} å ^{- γ k} ,                                      (3)

Γ(γ)

1 1 γ = Ñ_V 2 , C V = _γ ,

Э. Н. Оширов, П. Л. Абидуев, О.Ц. Мерхинова. Интегральное уравнение регулирования стока где CV – коэффициент вариации. При таком распределении

F ( k ) = ^Y [k ^Y - 1 e- k _dk . r ( y ) к

^Y - 1 e ^{- Y (} x ⁺ “ - y ) dy .

Имея в виду (3) и (4), уравнение (2) будет иметь вид:

ф ( x) = -7 - j ( a + x) ^Y - 1 e" ^{Y ( a + x)} d( a + x) + "Y^WУ r⁽ Y ) J + x                             ^{r (} Y ) 0

Уравнение (5) аналитически разрешимо при всех целых значениях параметра у.

При дробных значениях у интегралы не поддаются интегрированию в элементарных функциях и решение уравнения (2) сводится к решению системы линейных алгебраических уравнений.

Вот некоторые решения уравнения (2):

• 1)    Y = 1 ,

Ф (^x) =

e ^x

е “ - в’

0 <  x <  в ;

• 2)    Y = 2 ,

Ф ^(х) =

3(2x + 2 a + 1)e ^{- 2( a + x)} - 2 p (4p³ - 6 x p + 3 P - 6х)е ^{- 2(x+2 a} )

3 - 12 ав е^ - 4 p ⁴e ^{- 4} “ 0 <  x <  в

,

• 3)    Y = 3 ,

^ ( о ) = a^{-30 - 3} “

9 27 1      ,

• ⁹    + — A I x² + ( 9 a + 3 + 27 A a - 27 B ) x +

2 2 J     ^{V                        7}

Г 9 .           27 .             27

+| - a ² + 3 a + 1 + — a² A - 27 a B + — C

, 0 <  б <  р.

Здесь параметры А, В, С определяются из системы уравнений:

9 , 27   , 27         27 ,             27

(e ^{- 3 a} - - P - 2 ap - ^-7 aP ) А + (47 p + 27 aP ) В - 2 P C = B i ,

J -(— p + 9 ap ³ + ²⁷ a³ в ²) А + (e^{3 a} + - p ³ + ²⁷ ap ²)B - ²⁷ p C = B₂ , 8              4                        2          4²

-(f7 в" + T aP + - a2P3) А + (^7 в" + -aP3)B + (e3a - - P3)C = B3, где r 3 , 9    „ 3 „ 9 „

B i = 2 в + 2 ap + 2 P + 2 J в + 3 aP + P ,

< B 2 = 8 P + 3 aP ³ + p ³ + 4 ap + 2 ap ² + ^^

D 9 05 9 „4 3 „4 3 2 „3 o3 P BA = — в +— aP +— в +— aP + aP +

3 10     4       4     23

Рассмотрим, например, решение уравнения (6). Если a = 0,6, в = 0,4, тогда (6) имеет вид:

^(о) = 0,703а-о, 0 < x < 0,4.(7)

По этой формуле можно найти все вероятности наполнения объема в = 0,4 до любой отметки x . Если x ) в , то формула (7) указывает на переполнение объема в , т.е. холостой сброс.

Если в объеме β уровень х 〈 α , то получим дефицит отдачи, которые можно определить из соотношений:

β f1(x) =F(α-x)+∫ϕ(y)g(α-y-x)dy, 0≤x≤α-β.(9)

α-x f2 (x) = F(α-x)+ ∫ ϕ(y)g(α- y - x)dy , α-β≤ x <α.(10)

Согласно (9), (10) и (7) функции дефицитов отдачи имеет вид:

г ex f1(x)= α ,   0≤x<α-β,

e -β f2(x) =e-(α-x) +(α-αx)e-(α-x) , α-β≤x<α.

e -β

Используя (7) и (11) при α = 0,6, β = 0,4 получим следующий график.

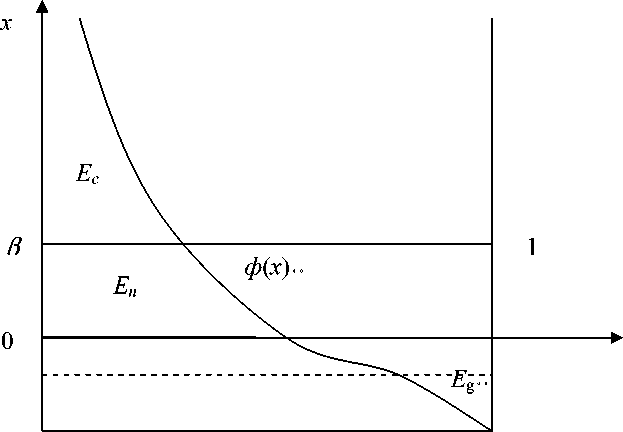
ф(х)

Из графика следует, что площадь Е с – объем слива, Е n – объем наполнения, E g – объем дефицита. Имеем

∞

Е с = ∫ ϕ (у) dy , Е g = α - β

β

β

∫ f ₁( x ) dx + ∫ f ₂( x ) dx , Е n = ∫ ϕ ( x ) dx . 0              α - β                 0

Можно проверить соотношение Е с + Е g = 1.

Физически Ес – означает, что данная емкость переполнена после отъема отдачи α и эту часть воды нужно слить. Еg – объем воды в хранилище недостаточен для удовлетворения объема α , поэтому в любой заданный момент времени объем недостачи будет равен Еg. Еn – в любой заданный момент времени в водохранилище будет заполнено в данном объе- ме.