Интегральные представления в краевых задачах о расчете устройств СВЧ- и КВЧ-диапазонов

Интегральные представления в краевых задачах прикладной электродинамики включают в себя фундаментальные интегральные соотношения типа леммы Лоренца и закона сохранения энергии, функциональные связи между краевыми задачами на дифференциальных уравнениях с интегральными уравнениями, соотношения ортогональности собственных функций однородных краевых задач, представления полей в форме непрерывного спектра собственных функций, интегральные функциональные соотношения типа формулы Грина, математическую интерпретацию задач излучения, использующих принцип Гюйгенса – Френеля, и т. д.

Интегральные представления используются для контроля получаемых результатов (это особенно важно при формулировке краевых задач в незамкнутой форме); в ряде случаев (по крайней мере, в асимптотике) позволяют получать аналитические решения; приводят к самосогласованным задачам, учитывающим обратное влияние поля излучения на первичные источники; позволяют получать априорную информацию о спектре возможных решений; решать присоединенные задачи как специфические задачи о возбуждении и т. д.

Все это предопределяет значительный интерес к различным видам интегральных представлений в прикладной электродинамике.

1. Интегральные представления в несамосопряженных и самосогласованных краевых задачах расчета неоднородных электродинамических структур

Поля в однородных и кусочно-однородных направляющих структурах описываются краевыми задачами на однородном уравнении Гельмгольца. Граничные условия для полей волн экранированных направляющих структур с идеально проводящими поверхностями или волн открытых структур, поля которых удовлетворяют нулевому граничному условию на бесконечности, являются однородными. Если экранирующая поверхность импедансная или в спектре открытой структуры рассматриваются несобственные волны, то граничные условия становятся неоднородными. Такая задача на однородном уравнении Гельмгольца с частично неоднородными граничными условиями называется полуоднородной. Ветви решений полуоднородной и однородной краевых задач на плоскостях волновых чисел могут быть связаны друг с другом в том случае, когда они являются решениями интегрального уравнения Вольтерра, записываемого в виде

x

n

u ( x ) = ^ cvMx )-XJ K ( x, ^) u (^) d ^• v=1             a

С использованием метода последовательных приближений для решения интегральных уравнений могут быть получены волновые числа круглых волноводов, однородно заполненных взаимной и невзаимной средой, с продольно намагниченным ферритовым стержнем, открытых диэлектрического, продольно намагниченного ферритового волноводов.

Переход от краевой задачи к интегральному уравнению позволяет на основе асимптотических решений последнего получить априорную информацию о спектре волн направляющей структуры, тем самым определить предмет поиска при решении дисперсионных уравнений.

В качестве примера рассмотрим задачу о расчете полного спектра волн открытого диэлектрического волновода (ОДВ). Функции, описывающие радиальную зависимость поля волн ОДВ, удовлетворяют уравнению Бесселя. В [1] показано, что краевая задача на этом уравнении при условии ограниченности поля по радиальной координате в общем случае в области r >  а ₅ имеет решение u ( a , r ) , удовлетворяющее интегральному уравнению

⁷ sin a ( r - r ‘

u ( a,r ) = e - i ^{a r} - J        ⁽) p ( r ' ) u ( a , r ' ) dr ' ,         (2)

r где a§ - значение r, соответствующее наперед заданному 5 > 0, для которого решение уравнения (2) при r ^7 имеет асимптотическую запись u (a, r ) = e - iar в областях волнового числа a:

первая область-Im a> 0; |a|>5 ;

вторая область-Im a< 0; a* 0; o ( r )/| a|< 1,

откуда следует, что на критических частотах поверхностные волны могут переходить только в несобственные комплексные волны, а собственные комплексные волны могут существовать в областях частот, удаленных от критических частот поверхностных волн.

Расположение корней дисперсионного уравнения в плоскости поперечного сечения волнового числа a 2 внешней области (вне ДВ), соответствующее приведенному выше рассмотрению на основе интегрального уравнения (2), приведено на рис. 1.

Разрез на комплексной плоскости a 2 =^ 2 + i 5 2 , которому соответствует Р 2 = 0 ( Р = Р 1 + Ф2 — продольное волновое число), проходит по отрицательной мнимой полуоси ( § 2 <  0) и частично по действительной полуоси у 2 >  0- Он разделяет два

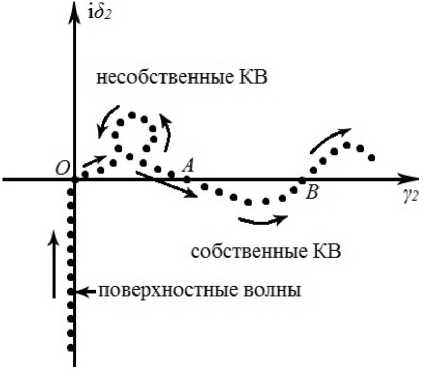
Рис. 1. Корни дисперсионного уравнения волн круглого открытого ДВ в плоскости волнового числа « 2

Fig. 1. Roots of the dispersion equation for the waves of a circular open DW in the plane of the wave number a 2

листа римановой поверхности комплексной функции p . Решения дисперсионного уравнения, изображенные на рис. 1, находятся на верхнем листе римановой поверхности, которому условно соответствует Р 2 <  0. Стрелки на рисунке указывают движение корней при уменьшении частоты.

В точке О , в соответствии с (4), поверхностные волны переходят в быстрые несобственные волны (вытекающие). Их поля, в соответствии с (3), нарастают по радиальной координате. В точке А вытекающие волны переходят в собственные комплексные волны, поля которых удовлетворяют условию излучения Зоммерфельда. В точке В собственные комплексные волны вновь переходят в вытекающие, которые затем (при уменьшении частоты) переходят в медленные несобственные волны. Таким образом, интервал АВ , предсказанный на основе рассмотрения решения (3) интегрального уравнения и областей его существования, полностью соответствует получаемому из дисперсионного уравнения краевой задачи.

Рассмотренный пример наглядно интерпретирует возможность априорного исследования спектров волн направляющих структур на основе сопоставления краевых задач и интегральных уравнений Вольтерра с использованием их асимптотических решений.

Решения несамосопряженных краевых задач, соответствующие собственным КВ, демонстрируют самосогласованность этих задач. Действительно, природа собственных КВ объясняется распределенным разворотом потока мощности, в результате которого обратный поток мощности замыкается через источник и влияет на него. Возникает замкнутый цикл, соответствующий самосогласованной задаче и приводящий к комплексному резонансу (КР). Таким образом, несамосопряженные краевые задачи, в которых образуется связь поля излучения с первичным источником, оказываются самосогласованными.

Интегральные представления оказываются полезными в задачах об излучении направляющих экранированных структур в открытое пространство, которые являются базовыми при построении систем проектирования апертурных антенн. Апертурные антенны – это антенны, излучающие с площади раскрыва, называемого апертурой. К таким антеннам относятся рупорные антенны, линзовые, зеркальные, волноводно-щелевые и т. д. По их излучающим поверхностям протекают электрические и магнитные токи высокой частоты (поверхностные токи). Апертурные антенны применяются главным образом в СВЧ- и КВЧ-диапазонах. Их линейные размеры много больше длины волны, что позволяет создавать остронаправленное излучение. Они находят широкое применение в радионавигации, радиоастрономии, в системах управления искусственными спутниками Земли и космическими кораблями, в тропосферных линиях связи.

При расчете поля излучения апертурной антенны определяют распределение поля на ее раскрыве. Каждый элемент площади раскрыва можно рассматривать как источник Гюйгенса – Френеля, который создает поле в точке наблюдения. Результирующее поле определяется путем суммирования полей, создаваемых в точке наблюдения всеми элементами поверхности раскрыва. При этом поля на поверхности раскрыва заменяются (согласно принципу Гюйгенса – Френеля) на эквивалентные поверхностные токи (электрические и магнитные [2]).

Строгость или нестрогость данного подхода к расчету поля излучения зависят от того, каким образом определяется распределение электромагнитного поля на раскрыве апертурной антенны. В большинстве случаев для этого используются методы геометрической оптики, когда не учитываются дифракционные явления на краях и внешних поверхностях раскрыва и обратное влияние поля излучения на распределение поля первичных источников. Более строгий анализ и экспериментальная проверка показывают [3], что приближенность определения первичного поля приводит к заметным ошибкам в расчете поля излучения в области боковых и задних лепестков диаграммы направленности. Строгая теория антенн приводит [3] к интегральным уравнениям. При этом, как правило, поднимается вопрос самосогласованно-сти задачи об излучении. Под самосогласованно-стью в большинстве случаев [4] понимают сведение задачи к сингулярному интегральному уравнению относительно функции тока на апертуре антенны, учитывающей влияние внешнего поля на распределение этого тока. Однако при этом в записи первичного поля учитывается ЭДС сторонних сил [4], что приводит к неоднородному интегральному уравнению (системе уравнений), что, вообще говоря, нарушает смысл самосогласованности задачи, так как в конечном итоге приводит к расчету поля излучения по заданным источникам. Самосогла-сованность в этом случае как таковая отсутствует. В строгом представлении самосогласованная задача – замкнутый цикл, содержащий обратную связь наподобие системы автогенератора. В результате наличия указанной обратной связи самосогласованная задача об излучении должна приводить к однородным интегральным уравнениям, то есть должна быть задачей на собственные функции и собственные значения. Последние являются решениями характеристического уравнения. Только на решениях этого уравнения получаются [5] нетривиальные решения краевой задачи об излучении.

Интегральные представления находят применение во внутренних задачах электродинамики. Широко используемыми методами расчета электродинамических структур являются метод частичных областей (МЧО) и различные импедансные методы [6]. При решении внутренних задач электродинамики, как правило, для представления полей в частичных областях используют дискретные спектры собственных функций этих областей. Однако это корректно только в тех случаях, когда для выделенных областей можно сформулировать краевые задачи Штурма – Лиувилля [7]. Если среди частичных областей, на которые разбивается электродинамическая структура, имеются такие, для которых нельзя поставить указанную краевую задачу Штурма – Лиувилля, нужно вводить непрерывный спектр собственных функций, то есть представлять поле в виде интегралов по волновым числам.

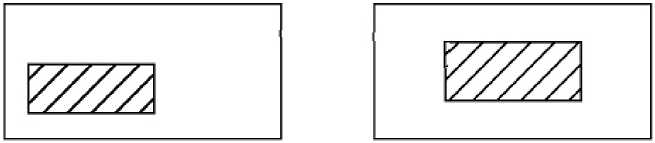
На рис. 2 приведены схематические изображения некоторых электродинамических структур, разбиение которых на частичные области не приводит к краевым задачам Штурма – Лиувилля.

а

б

Рис. 2. Схематические изображения направляющих структур: а – прямоугольные волноводы с частичным регулярным диэлектрическим и металлическим заполнением; б - излом прямоугольного волновода

Fig. 2. Schematic images of guiding structures: a – rectangular waveguides with partial regular dielectric and metal filling; b – break of a rectangular waveguide

Любое разбиение приведенных структур на частичные области приводит к краевым задачам со свободной границей, что не дает возможности сформулировать для них однородные краевые задачи с дискретными спектрами собственных функций. Области же хотя бы с одной свободной границей требуют введения непрерывного спектра, то есть интегрального представления поля, которое должно приводить к интегральным уравнениям (системам уравнений) относительно спектральных амплитуд. Только интегральное представление поля позволит корректно сформулировать краевые задачи. Впервые использование непрерывного спектра было осуществлено, по-видимому, при расчете параметров прямоугольных коаксиалов [8].

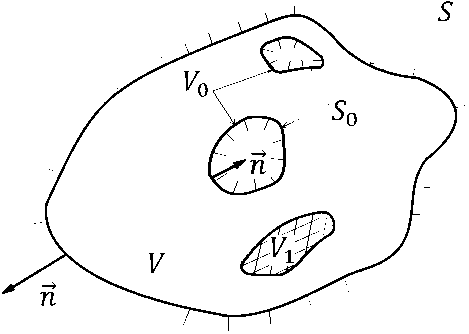
Рис. 3. Трехмерная область V

Fig. 3. Three-dimensional region V

Сформулируем скалярную краевую задачу на уравнении Гельмгольца для трехмерной области V, изнутри ограниченной поверхностью So , снаружи - S . Скалярная функция у может описывать распределение электромагнитного поля в объеме V , удовлетворяя уравнению Гельмгольца Ду + к 2 у = 0                                    (5)

и граничным условиям Дирихле, Неймана, Штурма - Лиувилля в замкнутом объеме. В (5) к о = ю/и , где и - скорость распространения колебаний.

На рис. 3 поверхности S o ограничивают области проводимости; объем V - область, заполненная диэлектрической средой.

Для многосвязной области V запишем [5] формулу Грина:

j ( y LG - GL у ) dV = ф|у — - G J dS ,          (6)

V                    S ^            j где S = S - So ; S - суммарная проводящая поверхность, ограничивающая объем V; n - внешняя по отношению к области V = V - Vo нормаль; G -функция Грина, удовлетворяющая уравнению

LG = Д G - к ² G = 5 ( г - F 0 ),                           (7)

в котором г - текущая координата, Г о - точка особенности функции Грина.

Используя (7) и свойство дельта-функции, получаем:

у ( ^Fo) = G ^ dS.                    (8)

^о           d п     d n )

S

Обозначая функцию поля у на поверхности S о как у о и удаляя поверхность S в бесконечность или задавая на ней нулевые граничные условия, переписываем (8) в виде

У ( г₀ ) ^fvoI G - G “Т ⁰ dS.                   (9)

/ n     a n j

S ₀

Положив Г о = 0, берем в качестве функции G функцию Грина свободного пространства:

1 e - ikr

4 n r

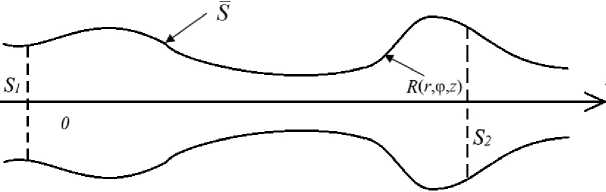
Рис. 4. Продольно нерегулярная направляющая структура

Fig. 4. Longitudinally irregular guiding structure

При этом из (9) получаем выражение для функции поля v ( г ) в произвольной точке пространства V как интеграл от V o по поверхности, ограничивающей это пространство изнутри:

интегральные уравнения (системы уравнений) относительно распределения полей на поверхности направляющей структуры, формулировать задачи о возбуждении, записывать условия ортогональности в задачах дифракции.

Интегральная запись f{[ E 1, Й2 И E2, H1 ]} dS =

S

=J ( — e — ^— e E 1 — ^— m H 2 + ^—* m H 1 ) dv

V леммы Лоренца связывает системы токов —e, —m, —e, —m с полями Ep Й1 и E2, H2 соответственно внутри отрезка направляющей структуры, ограниченного боковыми поверхностями S1, S2, так что S = Sо + S1 + S2. Объем V ограничен поверхностью S.

v ^{( —} ) = ^-ф V o ^[ e 4 п j     дn

S ₀

V

V

.— ikr )

—

r

No d n

e

—

-ikr Y

—*

— dS.

r

V 7 7

Выражение (10) - интеграл Гюйгенса - Кирхгофа. Положив г = г , приходим к интегро-диффе-

S ₀ ренциальному уравнению относительно функции

V o на поверхности S о :

Л

,—   1 X      д e

V o ^{( r} )  , ф Vo— -

4 п J     5 n

S ₀

V

.— ikr )

—

r

V 7

^dV o d n

e

- ikr Y

—

^— dS .

r

V 7 7

Оно является математической интерпретацией самосогласованной задачи по нахождению фун к ции v в произвольной точке внутри области V по распределению этой функции на поверхности, ограничивающей объем V изнутри. Как видно из (11), самосогласованная задача приводит к однородному интегральному уравнению Фредгольма 2-го рода, то есть является задачей на собственные функции и собственные значения, найдя которые, по формуле (10) можем определить функцию v в произвольной точке пространства, ограниченного поверхностями S и S о .

Формула (10) приводит к условию излучения:

lim r ²

r ^да

д

^V o Ш

V V

e — ikr ^

r

^dv 0 e ikr

dn    r

^{V 7} 7

= 0,

которое в антенных задачах позволяет однозначно определить поле излучения апертурных антенн.

В случае однородных краевых задач интегральное представление леммы Лоренца приводит к записи условий ортогональности полей собственных волн (колебаний), позволяющей решать задачи о возбуждении и задачи дифракции. Таким образом, целый ряд фундаментальных интегральных представлений является следствием интегральной записи леммы Лоренца.

Сформулируем краевую задачу для пространства, ограниченного поверхностью S , описываемой непрерывной функцией R ( r , ф , z ) , где r , ф , z - цилиндрические координаты, рис. 4. Проводящая поверхность S образует направл я ющую структуру. Соответствующая поверхности S продольная координата z с ( —да , да ) . Внутри указанного пространства расположены источники:

— 1 ^e >  m , — 2 e , m , - ^ ' m , (13)

3. Метод интегро-дифференциальных уравнений на основе интегрального представления леммы Лоренца

Интегральное представление леммы Лоренца является фундаментальным соотношением, позволяющим в чисто физической трактовке составлять

которые создают, соответственно, поля: —   ——   —    —   —

E 1 , Й 1 ; E 2 , Й 2 , - E_n , H_N .                     (14)

Таким образом, имеем N неоднородных краевых задач в пространстве, ограниченном поверхностью S = S + S 1 + S 2 , где S - боковая поверхность выделенного объема, S 12 - торцевые поверхности (поперечные сечения волновода), ограничивающие с двух сторон объем V .

Источники (13) находятся в конечной области V , под которой можно понимать: продольно-нерегулярный волновод (в частности, периодиче-ски-нерегулярный); нерегулярный участок волноводного тракта; волноводный переход и т. п. Таким образом, имеем задачу о возбуждении поля множеством источников. Поле образуется совокупностью полей собственных волн, связанных

В неограниченном пространстве ( S ^ « ) источники j ^m создадут поля расходящихся сферических волн, удовлетворяющих условию излучения, которые на поверхности S ^« обращаются в нуль. Обозначив эти поля как Е ⁰ , H ⁰ , уравнение (17) перепишем в виде

нерегулярностями волновода и удовлетворяющих граничному условию:

Е т к ⁼ 0, (15) и соответствующих собственным волнам рассматриваемого волновода. Поля, на которые не накладывается условие (15), удовлетворяют условию излучению на бесконечности.

Волны Е i , H i могут быть как направляемыми волноводными волнами, так и волнами, излучаемыми в открытое пространство. При этом про-

J ( ^E n - ^j e^{E 0} - ^H n + ^H ⁰ ) dV = 0.         (18)

V „

Поскольку в (18) интегрирование производится по месту расположения токов, интеграл по бесконечному объему в (18) тождественно совпадает с интегралом по конечной области источников, т. е.

в ⁽¹⁷⁾ J = J .

V V ®

Исключая из (17) с помощью (18) токи j ^’ m , получаем:

странства, соответствующие различным краевым задачам, имеют одну общую область V , в которой распределены источники (13), создающие поля (14) то есть указанные пространства объединяются областью источников.

Поля первой категории (обозначим их как Е к , H к ), удовлетворяющие граничному условию (15), соответствуют собственным волнам нерегулярного экранированного волновода. Поля второй категории, удовлетворяющие условию излучения, на поверхности S могут принимать любые конечные значения. Их обозначим как Е n , H n . Поля Е к , H к будем полагать искомыми решениями краевой задачи, поля Е n , H n будем рассматривать как вспомогательные. Источники, создающие поля первой категории, обозначим как j ^m , источники создающие поля второй категории, обозначим как ^m .

Для полей Е к , H к и Е n , H n в объеме V лемма Лоренца запишется как

^{ [ ^E к ’ H n ] — [ ^E n ’ H к ] } ds =

^S                                                          (16)

= J ( j e^En - j e^Eк - j m H n + j m^Hк ) ^dV .

V

При S 1 2 ^ ±« с учетом конечности площади поперечного сечения рассматриваемого нерегулярного волновода и граничного условия (15) уравнение (16) перепишется в виде

J [ ^H к^Е n ] ds =

S

= J ( ^E n - rE к - i k H n + ^ m H к ) dV .

V

J [ ^Й к^Е n ] ds =

S

[ 1 e 1 ⁰ 1    1 m j ⁰ J 1/7V

= J [ j n ( ^Ек ^{- Е}к ) ^- j n ( ^Йк ^{- Й}к ) ] ^dV .

V ®

Выбрав в качестве источников j ^ ’ m элементар-

ные диполи:

^{1 е} , m j_n

¹ e , m

In

1 где r ,m jn

5 I ¹ - 1 e, m

V j n

– координаты вспомогательных источни-

ков, и воспользовавшись свойством 5 -функции,

из (19) получаем:

J [ ^Й к^Е n ] ds = I n

S

m

In

^Hk ⁰

m

n

E k ⁰

-

E k

r ^j

e n

r j

n

^{- Й}к

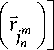
В (²⁰) ^{Е 0} f j 1 ’ ^Ек f j 1 ’ ^Йк f j 1 ’ ^Йк f j 1 —

V j n у V j n у V j n 7 V j n 7

проекции векторов на направления элементарных ¹

диполей j ne ’ ^m .

Поля E к , Йк в (20), удовлетворяющие гранич-

ным условиям:

Е = 0; Й = 0 т S           n S

( H n - нормальная составляющая),

можно рассматривать как поля собственных волн в волноводе с идеально проводящей экранирующей поверхностью S . В решаемой задаче эти поля будут искомыми полями нерегулярного волновода. Поля: Е 0 , H 0 , Е n в (20) являются вспомогательными. Они создаются диполями ^’ П^ в неограниченном пространстве и стремятся к нулю

при удалении от источников как поля расходящихся сферических волн.

Вспомогательные излучатели — **^m расположим 0                          ^— e , m

, а источники j k_* , создающие поля собственных волн рассматриваемого волно-

—О вода, отнесем в сечение z ^ -да. Поскольку Е^, H0 - поля сферических волн, создаваемых источниками, отнесенными в бесконечность, в месте расположения диполей П’m в сечении z = 0 в силу неравенств:

E

0 k

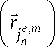
<< E k

—*

Г . ™ r ^e *^m j_n

;

^Hk ⁰

<< H_t

—

Г „ ™ r ^e * ^m j_n

ими в уравнении (20) можно пренебречь. Тогда это уравнение перепишется:

[ H_k E — ] dS = - I *E_k I ^— e 1 + i m H I ^— m 1.            (22)

nn  n

• •L                          \ n J           \ n J

S

Полученное уравнение (22) является интегральным (в общем случае интегро-дифференциальным) уравнением относительно полей Е к , H_к . В тех случаях, когда вводится один вспомогательный источник (одного типа), получаем уравнения: J [ ^Й к^Е n ] ds =- I n E k ^{f j} e ¹ ;

\ n J

^S                                                           (23)

J [ H * k E n ] dS = I m H k I ^j m ¹ .

\ n J

S

Амплитуды вспомогательных источников, входящие в обе части уравнений (23), в процессе решения уравнений сокращаются, поскольку Е _n ~ ^*^m .

Согласно задаче о возбуждении волн экранированного волновода, источники —**m создают в общем случае бесконечные наборы собственных волн, поэтому поля Е—к и Йк следует представлять в виде да                           да

^Ек = Е A v E v ; ^Hк = Е B v iH v                (24)

v= 0                v= 0

для каждого фиксированного « k », то есть для каждого источника.

Используя метод коллокаций, алгебраизацию уравнений (23) можно производить, подставляя в них поля в виде (24) и записывая их в точках вспомогательных источников, число которых берется в соответствии с числом членов в суммах (24). Поля Ev, ЕЙv в каждом сечении z записываются как поля волновода сравнения, соответствующего этому сечению. Суммирование в (24) ведется по полям волновода сравнения толщиной dz, удовлетворяющим в пределах этого волновода граничным условиям (21). Это обеспечивает выполнение граничных условий в целом. Непрерывность поля по продольной координате обеспечивается самими интегральными уравнениями (23). Каждому ис- точнику —**m соответствует свой набор полей (24), определяющий k-ю волну нерегулярного волновода. Номер собственной волны нерегулярного волновода определяется порядковым номером корня трансцендентного дисперсионного уравнения.

Метод интегро-дифференциальных уравнений на основе интегрального представления леммы Лоренца является универсальным, пригодным для расчета как неограниченных продольно-нерегулярных экранированных направляющих структур, так и отдельных нерегулярных (плавных и скачкообразных) участков волноводного тракта, в том числе и неоднородно заполненных.

• 4. Самосогласованная задача о комплексном резонансе на основе интегрального представления леммы Лоренца

В поперечно-неоднородных (слоистых) направляющих электродинамических структурах, описываемых несамосопряженными электродинамическими операторами, могут существовать, даже в отсутствие диссипации энергии, волны с комплексными волновыми числами – комплексные волны (КВ). Источники, описываемые действительными функциями координат, возбуждают, в частности, в двухслойном круглом экранированном волноводе по обе стороны от себя по две комплексно-сопряженные волны с противоположно направленными фазовыми скоростями. Это приводит к возникновению стоячей волны, поле которой локализовано вблизи источника. Поскольку отмеченное явление обнаруживает резонансные свойства не на одной частоте, как при обычном резонансе, а во всем диапазоне существования КВ, оно классифицировано как «комплексный резонанс» (КР).

Поскольку комплексный резонанс возникает в результате взаимодействия двух комплексных волн, приводящего к образованию специфического (локализованного вблизи источника) поля стоячей волны, первостепенным является вопрос ортогональности этих волн. Решение его позволит определить пары комплексных волн, образующих указанное поле стоячей волны, и выяснить условия возникновения комплексного резонанса. Кроме того, поскольку в реальных условиях комплексный резонанс наблюдается в ограниченных по длине отрезках направляющих структур, необходимо выяснить вопрос о взаимодействии комплексных волн, приводящему к возникновению взаимных потоков мощности, нарушающих условия существования комплексного резонанса.

Как известно [9], существование в плоскостях поперечных волновых чисел (а^) пары комплексно сопряженных решений дисперсионного уравнения волн круглого двухслойного экранированного волновода обеспечивает существование в этом волноводе четырех комплексных волн, которые условно можно представить в виде:

e ^- i ⁽Р 1 + i ^e 2 ) z (I),

С учетом (27) из равенства (30) следует, что поля комплексных волн I и II удовлетворяют математическому условию ортогональности:

J [ E n . H k ] d ^S - 0,

S

ei(р1 -ip2)z (II), e-i(A-ie2)z (in),

e i (P i + i p 2 ) z (IV),

где P i >  0, P 2 <  0, z — продольная координата направляющей структуры.

Являясь собственными волнами экранированного волновода, комплексные волны (25) удовлетворяют условию ортогональности, следующему из леммы Лоренца

-     -          -     -        — I N, кn

J([ En , Hk Н Ek, Hn ]) d         k ,-,,,<26

S где S – поперечное сечение волновода; n и k – индексы волн (25).

Понимая в (25) под E n и H n поля комплексной волны I, а под E к и H к - поля волны II и учитывая связи этих полей: —*        —*          —*           —*

E n - ^Ek ; H n - - H k ,                            ⁽²⁷⁾

которые являются следствием комплексной сопряженности решений (a^) дисперсионного уравнения, соответствующих указанным волнам, получаем:

Re J [ E_n , H n ] dS - 0.                                (28)

S

Аналогичным образом из совместного рассмотрения волн I и III (им также соответствуют комплексно сопряженные в плоскостях поперечных волновых чисел а^ решения дисперсионных уравнений) получаем:

Im J [ E n , H n ] dS - 0.                              (29)

S

Равенства (28) и (29) демонстрируют известный [1] факт: комплексные волны не переносят мощности в среднем за период, то есть

J [ E n , H n ] dS - 0,                                   (30)

S где под E-n и H- n понимаются поля любой из комплексных волн (25).

из которого следует отсутствие взаимного потока мощности этих комплексных волн.

Таким образом, можно сделать вывод, что, поскольку взаимный поток мощности в среднем за период комплексных волн I и II равен нулю, взаимодействие этих волн, возбужденных с одинаковыми амплитудами, должно приводить к образованию поля стоячей волны, которое, в свою очередь, приводит к возникновению комплексного резонанса.

Теперь рассмотрим две волны I и IV, которым на комплексных плоскостях поперечных волновых чисел a i 2 внутренней и внешней областей двухслойного волновода соответствуют одни и те же точки, являющиеся изображениями решений дисперсионного уравнения. Указанные волны описываются продольными компонентами векторов Герца:

П z , m -у e , m ( r , ф ) e ± i P z , (32)

где P - P i + 1 P 2 , а знаки «-» и «+» соответствуют волнам I и IV.

Для продольных компонент комплексных векторов Умова - Пойтинга волн (32) получаются вы-

ражения:

^Sz 1,2 ^-

| Р| dv e Sv m r Id r d

, 2 S m e * бцю dy dy

r | дф дr

Г

± toeP

ду^e д r

Г

± ЮцР

ду ^m д r

dyedy m дф д r

ду m ду^e д r дф

1 ду^e r²дф

2 )

±

ду ^m дф

2 )

.e-2P2z

где индекс «1» и знак «+» соответствуют волне I, индекс «2» и знак «–» – волне IV.

Продольная компонента взаимного комплексного вектора Умова - Пойтинга волн I и IV с учетом того, что e, m (IV)          e, m (I)

ду       ду дф        дф запишется в виде:

^Sz 1,2 =

бцю² дф^m дф^e + дф^m дф^e

—

r

дф д r    д r дф

—

| ₽|²f дф^e дфm

—

r

+ toeP

дф д r

дф^e дф^m д r дф

+

дф^e д r

дф^e

2 ^

—

2 дф

f

— юцР

дф ^m д r

1 дф^m

2 М

дф

1—2 ip! z e •

Обозначив

дф^e дф ^m* д r дф

= a + ib;

toJ£

S

дф^e д r

1 дфe r2 дф dS = x;

дф^e дф^m *     .,

—  — = c + id; дф д r

_Ю|ц

S

дф ^m д r

1 дф m r2 дф dS = y

2 ^

и предположив, что

J Sz 1,2 dS = 0;

S

J Sz 1,2 dS = 0,

S

получаем две системы линейных алгебраических уравнений относительно x и y:

x+y=

1 a — c f 2

—        БЦЮ +

P1^{J r} I

x — У = ]1 J bTd^fe^®² —1₽|² 'j dS

P2 s^r

из уравнения (35) и

1 a + c f 2 X — y = —          I БЦЮ ■ e1 S r v

1 b + d f 2 X + y =         I БЦЮ + e r v

S

из уравнения (36).

В общем случае системы уравнений (37) и (38) несовместны. Поскольку равенство (35) для комплексных волн является доказанным и физически обоснованным [9], из несовместности систем (37) и (38) следует некорректность предположения (36). Таким образом, предположение о равенстве нулю взаимного потока мощности комплексных волн I и IV в общем случае неправомерно. В результате

можно заключить, что взаимодействие двух комплексных собственных волн любой направляющей структуры, которым на комплексных плоскостях а12 соответствует одно и то же решение дисперсионного уравнения, может привести к возникновению потока мощности, среднего за период, отличного от нуля. В этом отношении комплексные волны I и IV оказываются подобными обычным реактивно затухающим волнам запредельного волновода.

На основании проведенного рассмотрения можно сделать вывод, что в ограниченных по продольной оси отрезках слоистых направляющих структур взаимодействие комплексной волны, возбуждаемой источником, с комплексной волной, возникающей за счет отражения от конца отрезка волновода, может нарушить режим стоячей волны, образующей комплексный резонанс. В результате в реальной ситуации комплексный резонанс не проявляет идеальных свойств, соответствующих бесконечной по продольной оси направляющей структуре. В частности, полоса частот, соответствующая комплексному резонансу, сужается по сравнению с полосой существования комплексных волн. В верхнем участке диапазона сужение происходит из-за возбуждения комплекс -ных волн на концах отрезка волновода, в нижнем – из-за уменьшения (вследствие большого затухания) запасенной в объеме энергии.

Рассмотрение задачи, описывающей КР с использованием интегральных представлений, позволяет утверждать, что это явление требует обязательного присутствия источника, через который замыкаются прямой и обратный потоки мощности, совместное существование которых и обеспечивает возникновение резонансного явления.

Заключение

Таким образом, использование интегральных представлений электромагнитных полей в краевых задачах прикладной электродинамики, связанных с расчетом СВЧ- и КВЧ-устройств, способствует совершенствованию методов решения несамосопряженных краевых задач, к которым, как правило, сводится электродинамический расчет подавляющего большинства функциональных узлов СВЧ. Указанные представления можно разделить на две большие категории: естественно существующие и интерпретирующие физические законы, например лемма Лоренца и теорема взаимности, и получаемые искусственно, например

переходом от краевых задач на дифференциальных уравнениях к интегральным уравнениям, введением непрерывных спектров собственных функций частичных областей. На примере рас- смотрения явления комплексного резонанса показано, что интегральные представления позволяют установить связь между несамосопряженностью и самосогласованностью краевых задач.