Интегралы Фейнмана как связующее звено между радиотехникой, фрактальной парадигмой и квантовой механикой

Отношение науки к мышлению лишь тогда истинно и плодотворно, когда становится видна пропасть, существующая между наукой и мышлением, притом такая пропасть, через которую невозможен мост. От науки в мышление нет мостов, возможен лишь прыжок.

Мартин Хайдеггер

A

AV

где q = x и p = - i ■ 5/5 x — операторы координаты и импульса соответственно (здесь и далее используется система единиц, в которой постоянная Планка Й = 1).

Функция Грина (ФГ) КвГО имеет вид [4]:

Методы квантовой теории применяются при исследовании вопросов, связанных с радиотехникой, уже давно. В частности, уравнения Дайсона и Бете-Солпитера используются в статистической радиофизике с 60-х годов прошлого века [1]. Однако сама диаграммная техника Фейнмана появилась благодаря введению Р. Фейнманом в квантовую механику интегралов по траекториям [2]. В данной статье описаны радиотехнические величины, которые могут быть выражены интегралами Фейнмана, и проведен анализ следствий, к которым приводит кванто-

G ( x , x ; t )

m ■ ю

2 ■ п ■ i ■ sin( to ■ t )

x exp i ■ m ■ ю■

( x ² + x ²) ■ cos( to ■ t ) - 2 ■ x ■ x

2 ■ sin( to ■ t )

Согласно общим правилам квантовой механики [3; 4], ФГ (2) – ядро унитарного оператора эволюции состояния КвГО в координатном представлении:

G ( x , x ; t ) =< x | exp( - i ■ t ■ H ) | x > .                 (3)

С другой стороны, ФГ (2) может быть вычислена как интеграл Фейнмана [2]:

вомеханическая интерпретация этих величин.

Рассмотрим одну из самых простых и одновременно наиболее значимых в физике квантовомеханических систем – одномерный гармонический осциллятор (КвГО) с частотой ю и массой m , т. е. систему с гамильтонианом [3]:

Q ( t ) = x

G ( x , 3 c ; t ) =    J exp

Q (0) = x

m ■to ² ■ q ²( t )

H =

'2         2 Л2

p m ■№ ■ q

2 ■ m       2

t i ■ J I P(t) ■ (t) —

0 ^V

■ dt ■ П - t

dp ( t ) ■ dq ( t ) 2 ■ n

p ²( t )

2 ■ m

(мы взяли интеграл Фейнмана в гамильтоновой форме [5–7]).

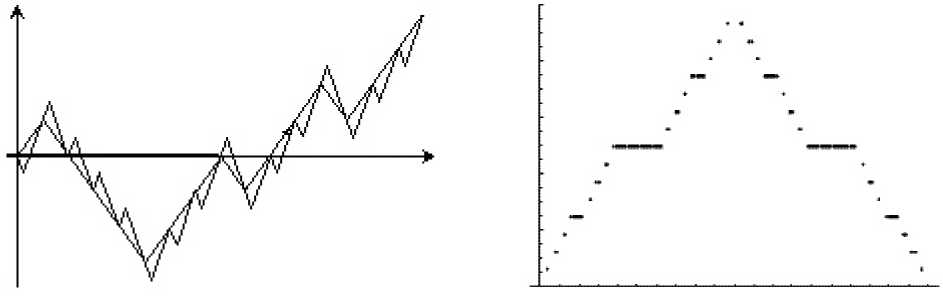
Рис. 1. Функция Больцано (слева) и функция Безиковича (справа)

Положим в формуле (2) t = п/(2 -to ), тогда:

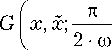
тогда интеграл по путям (6) вычисляется как предел конечномерного интеграла:

exp( - i - p - У = lim V2 - п - i x N ^^

m ^-ю , .

-------- exp( - i - m - to - x - x ). 2 - п - i

Сравнивая выражения (4) и (5) и переходя к системе единиц m = to = 1, делаем вывод, что

x J exp[ i - S n ( P , Q )] -

R 2 N ^{+ 1}

d N Q - d^{N + 1} P

(2 -п ) ^{N + 1} ’

плоская волна имеет следующее представление в виде интеграла Фейнмана:

exp( - i - p - У ) =

Q (п/ 2)=k -уп/

• = V2 - п - i - J exp i - J I P(t) - Q(t) -

• Q (0)=p/k0

• -        p 1 d _ц

2 J J

причем функционал классического действия заменен следующей функцией 2 - N + 1-й переменной:

N

S n ( P , Q ) = ^

j = 0

-

Ат

r

P j

V

^P j ^{- (} Q j + 1 ^- Q j ) ^-

^Q j ⁺ Q j ■ Qj + 1 ^{+ Q} 2 + 1

с мерой континуального интегрирования ( k ₀ – параметр с размерностью волнового числа, смысл введения которого выяснится в дальнейшем):

d ц = П t

dP ( t ) - dQ ( t ) 2 - п

в которой канонические переменные P ( т ) и Q ( т )

задают все возможные классические траектории в фазовом пространстве, соединяющие начальную и конечную точки [5–7].

Конструктивно запись континуального интеграла в форме (6) означает следующее: разделим временной интервал [0, п/2] на N равных частей шириной Ат = п/(2 - N ) и аппроксимируем на них координату Q ( т ) кусочно-линейными функциями, а импульс P ( т ) — кусочно-постоянными функциями:

Приближение (8) для фазовых траекторий означает, что при стремлении N к бесконечности в множество функций, по которым ведется интегрирование по координатам в континуальном интеграле (6), попадает функция Больцано (см. рис. 1, слева), а в множество функций, по которым ведется интегрирование по импульсам, попадает функция Безиковича (см. рис. 1, справа). Обе эти функции непрерывны, но нигде не имеют производной – см. [8–11] и ссылки в них.

Фазовые кривые можно рассматривать и на фазовой плоскости ( P , Q ), которую удобно задать комплексными координатами:

a =

Q + i - P

- Q - i - P a =

Q ( т ) = Q j + ( Q j + i - Q j ) - ( т-т j )/ Ат , P ( т ) = P j ,     те [ т j , т j ₊ i ],

где P j = P ( т j ) и Q j = Q ( т j ) — значения канонических переменных в точках т j = j - Ат , j = 0, N ,

служащими для определения континуального интеграла в голоморфном представлении [5; 7] и переходящими при квантовании осциллятора в операторы уничтожения и рождения [3; 4]. Тогда траектории (8) представляются на фазовой плоскости совокупностью прямых, параллельных оси Q . Пополним это множество прямых

Рис. 2. Алгоритм построения кривой Пеано

теми прямыми, параллельными оси P , которые соединяют точки ( Q j ₊ 1 , P j ) и ( Q j ₊ 1 , P j ₊ 1 ) и соответствуют мгновенному изменению импульса в момент времени т j ₊ 1 . Таким образом, оказывается, что в числе фазовых траекторий на фазовой плоскости имеется и кривая Пеано с двумя концевыми точками (ее построение по алгоритму Гильберта см. на рис. 2.) – непрерывная кривая, заполняющая квадрат настолько плотно, что ее топологическая размерность равна двум [8].

Согласно теореме Банаха-Мазуркевича [8] множество дифференцируемых на отрезке функций является пренебрежимо малым в смысле категории Бэра по сравнению с множеством всех непрерывных функций на том же отрезке. Таким образом, интегрирование в континуальном интеграле (6) ведется в основном по недифференцируемым функциям, что отмечал и сам Р. Фейнман [2], и отечественные исследователи интегралов Фейнмана [6; 7]. Однако все они упускали из вида тот факт, впервые указанный авторами в докладе [12], что эти недифференцируемые функции обладают свойством фрактальности [8–11].

В качестве примера непрерывной, но нигде не дифференцируемой функции, задаваемой не правилом ее построения, а одной формулой, можно привести функцию:

® f (x) = ^ an ' r(bn ' x), n=1

0 <  a <  1, a ■ b >  1,

где r ( x ) – квазипериодическая функция. При определенных ограничениях на r ( x ) лакунарный ряд (12) нигде не имеет производной [8]. Функция (12) удовлетворяет следующему функциональному уравнению, отражающему свойство ее самоподобия:

f ( x ) - a ■ f ( b ■ x ) = a ■ r ( b ■ x ),                        (13)

а ее график обладает фрактальной размерностью [8]:

D = 2 + log b a ,                                 (14)

причем поскольку 1 <  D <  2, то график функции (12) – это уже не линия, но еще не поверхность.

Аналог кривой Пеано, задаваемый одной формулой, а не рекуррентной процедурой, также существует, а именно, в статье [13] был построен степенной ряд:

to

F ( z ) = ^ C n ■ z n , z = x + i ■ y ,               (15)

n = 0

сходящийся в открытом круге | z | < 1 и непрерывный в замкнутом круге | z | < 1, такой, что образ отрезка те [0,2 ■ п ] при отображении F (exp( i ■ т )) содержит непустое открытое множество на плоскости.

Далее, хорошо известно, что для аддитивной группы вещественных чисел R неприводимыми унитарными представлениями являются плоские волны exp( - i ■ p ■ У ) [14]. Они же являются собственными функциями известного из квантовой механики оператора Г a = exp( i ■ a ■ P ) сдвига на a [3; 4], который является ничем иным, как оператором регулярного представления группы R [14]. С другой стороны, тот факт, что плоская волна, а также собственные значения exp( - i ■ p ■ a ) оператора сдвига Г _a выражаются континуальным интегралом (6), при учете того, что интегрирование в нем ведется по фрактальным функциям типа функций Больцано и Без-иковича, означает, что формула (6) отражает связь непрерывного и дискретного.

Из определения преобразования Фурье произвольного сигнала f ( x ) е L ²( R ):

+to

F [ f ](P) = J exp(-i ■ p ■У) ■ f (У) ■ d У

-to в свете выражения (6) становится ясным, почему собственные функции гамильтониана КвГО (1) [3]:

| n >= ,    1       ■ Hn(У) ■ exp(- y2/2),(17)

\ 2n ■ n !■ Vn где Hn (У) — полиномы Чебышева-Эрмита [14], т. е.

H|n >= (n + 1/2) ■In > являются также собственными функциями оператора преобразования Фурье [3; 14]:

.F | n >= V2 ■ п ■ exp(- i ■ п ■ n/2) ■ | n > .(19)

Из формулы (6) также следует, что преобразование Фурье – это фрактальная операция. Что, в свою очередь, означает, что теория сигналов – фрактальна по своей сути. Поясним это на примере согласованных фильтров, оперирующих с сигналами известной формы и являющихся каноническими элементами многих радиосистем. На языке преобразований Фурье (15) это означает, что согласованный фильтр работает со спектром сигнала f ( x ). Отсюда немедленно следует вывод о том, что фрактальны и все существующие радиосистемы.

Наконец, по аналогии с «локационом» – введенной в [12] квазичастицей радиолокации – для адекватного описания этой ситуации необходимо ввести также и квазичастицу радиосистем – «радион» [15]: объект, двигающийся в фазовом пространстве по фрактальным траекториям подобно квантовомеханической частице. Согласно той же формуле (6) радион в некоторой степени «статичен», т. е. находится как бы «внутри» радиосистемы, занимаясь обработкой информации. Однако для радиосистем важна не только обработка информации, но и ее передача.

Чтобы прояснить вопрос о роли радиона в процессах передачи информации, рассмотрим распространение электромагнитной волны в среде с постоянной диэлектрической проницаемостью б:

= б 92 Е , =

A E = , divE = 0. (20) с ² d t ²

exp

'J 2 ■ п ■ i ■ т

Q ( k 0 ■ Z ) = k "У

i ■ ( У-Н )²

J exp i

Q (0) = k m

2 ■т

" k ■ z

J P ( т ) ■ Q ( т ) 0 v

-

P 2 ( т )

d т

■ d ц

с той же структурой фазовых траекторий, по которым ведется интегрирование, которая была подробно описана выше.

Далее, начальное распределение амплитуды формируется интегралом Фурье:

+®

A ( ^ , 0) =     a ( p ) ■ exp( i ■ p ■ ^ ) ■ ^p ,             (25)

2 ■ п

-да

в котором также фигурирует интеграл Фейнмана (6):

exp( i ■ p ■ У V- 2 ■ п ■ i

-

Q (0) = k 0 ■У         p 0 p

J exp - i ■ J I P ( т ) ■ Q ( т ) -

Q ( -п/ 2) = p/k ₀             -п/ 2

P 2ir)± Q 2^ Y d т

■ d ц -

Подставим в уравнения Максвелла (20) электрическое поле с напряженностью:

E = (0, A ( x , z ) ■ exp( i ■ k_Q ■ z - i ■ to ₀ ■ t ), 0), (21) где k = ® o ■ Ve / с , тогда в приближении квазиоптики [16] получим в безразмерных переменных т = kz и У = kx для комплексной амплитуды поля A ( У , т ) уравнение:

Сравнивая континуальные интегралы (24) и (26), приходим к выводу о том, что при т e [ - п/ 2,0) радион готовится к его излучению радиосистемой, в которой его как бы «запирает» квадратичный потенциал. В момент времени т = 0 этот квадратичный потенциал пропадает, и затем свободный радион продолжает двигаться в безразмерном времени по фрактальной траектории в фазовом пространстве ( P , Q ), что

d A _ 1 д ² A --- =------— . дт 2 ду ²

Временная эволюция амплитуды поля A ( У , т ) полностью определяется [16] ее распределением A ( У , 0) в начальный момент времени и известной ФГ уравнения (22):

A ( У , т ) =

V 2 ■ п ■ i ■ т

+да

■ I

exp

-да

i ■ К-4 )² '

2 ■т

■ A ( п , 0) ■ d H -

и соответствует его излучению радиосистемой в пространство. При этом комплексная амплитуда поля A ( У , т ) соответствует амплитуде вероятности радиона, а функция a ( p ) из интеграла Фурье (25) является для радиона его амплитудой вероятности по импульсам в начальный момент времени. Наконец, из формулы (21) следует связь т = © 0 ■ t безразмерного и размерного времен свободного радиона. Групповые свойства свободного радиона совпадают с аналогичными свойствами локациона, подробно описанными в докладе [17].

Поскольку для электромагнитного поля уже введены его кванты – фотоны, то принципи-

С другой стороны, уравнение (22) является уравнением Шредингера для свободной частицы единичной массы, поэтому его ФГ выражается следующим интегралом Фейнмана [2]:

ально важно исследовать вопрос о взаимоотношении радионов и фотонов.

Начнем с отношения фотонов к радионам: как

известно, квантование электромагнитного поля

основано на так называемом разложении поля

(в единичном объеме) на осцилляторы с частотами to ( E ) = с ■ | E | [18]. При этом оператор векторного потенциала поля имеет следующий вид [18]:

^A < * t ) = X < c E a A E a ( ^{r ,} t ) + ^C L A E a < ^{r ,} t » -    (27)

к a где взаимно ортогональные вектор-функции

—►

A ,* ( r , t ) =

E a^v ’

= V 4 ■ п ■

e^C E )         * _        *

,       _ r ■ exp( i ■ E ■ r - i ■ to ( E ) ■ t )

4 2 ■ to ( E )

удовлетворяют условию поперечности поля E ■ * ^{( a )}( E ) = 0, а операторы рождения и уничтожения фотонов подчиняются бозевским коммутационным соотношениям:

восьмимерном фазовом пространстве. В частности, примером такой траектории является восьмимерная кривая Пеано, заполняющая восьмимерный куб [8]. Кроме того, выражение плоской волны (28) в виде континуального интеграла до некоторой степени поясняет невозможность введения волновой функции фотона в координатном представлении [18].

Проделаем теперь наш путь в обратном направлении – от радионов к фотонам. С помощью производящей функции для полиномов Чебышева-Эрмита [14] найдем следующее разложение

ФГ (24): 1

+  1 е е

^{[ c} E a , c E c 'a' ] = ⁵ EE '⁵aa' ^.

V 2 ■ п ■ i ■ т где

■ exp

i ■ ( ^ - n ) 2

2 ■т

^x          nn

= X V^ ( n ) -^H , (33) n = 0o             n ^!

От операторного описания (27)–(29) электромагнитного поля можно перейти к классическо-

v ; ( n ) =

V 2 ■ п ■ i ■ т

x

му описанию электромагнитного поля с помощью уравнений Максвелла (20), если фотонов много, то есть если напряженность усредненного по промежуткам времени A t поля [18]:

I n I x H n I           I ■ exp

i ■ n

а

I E\>>

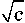
( V2 ■ i ■ т J

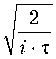
( с ■ A t )²

что в силу представления поля (21) накладывает

то же самое ограничение на величину амплитуды вероятности радиона A ( £ , т ).

Соотношение (6) легко обобщается на случай пространства Rⁿ [15]:

f n exp -i^ X pj лj

I j = 1 J =

(2 ■ п ■ i ) n²

Q ( п/ 2) = x

= j    exp( i ■ 5 [ P , Q ]) x

Q (0)=p x п n dPj(т) ■ dQj(т) j=1 т 2 П где действие

5 [ P, Q ] = п/ 2 f n                 n

= j X P j (т^ ^Q j ( т ) - X

0 I j = 1

j = 1

Р 2 ( т ) + Q j ^!( т )

■ d т .

Отсюда следует, что плоская волна в вектор-функции (28) задается интегралом Фейнмана (31) при n = 4, который может быть проинтерпретирован как статический радион, распространяющийся по фрактальным траекториям в

2 ■т ,

Подставляя разложение (33) в формулу (23),

получим:

да

А К, т) =X n=0

n

Ат -4= n n!

с коэффициентами

+®

А П = j v ; ( n ) ■ A ( n ,0) ■ d n .

-да

Разложение амплитуды вероятностей радио-на A ( ^ , т ) в степенной ряд (36) означает [5; 15; 19], что ему соответствует следующее состояние КвГО:

да

I V>= X An.-\n > .

n = 0

Но стационарные состояния КвГО (17) могут быть получены с помощью оператора рождения фотона (29) с импульсом E и поляризацией a следующим способом [18]:

\ n > =      ■ ( С +_а) n \0 > .

V n !    ^{E a}

Таким образом, связь радионов с фотонами тоже установлена.

Очевидно, что развитая выше для радионов схема без изменений переносится на распространение волновых пакетов в диспергирующей

среде во втором приближении теории дисперсии – и для случая, когда начальный сигнал задан на границе среды с законом дисперсии k ( to ) [16]:

— exp < - г ■

^т f

JdТ^ V т г

1     5

г 5 F ( т )

S X

8 A 1 d2 k (Юо) 82 A 8z 2 d to2 8т2 , т — t - dk^l ■ z; (40)

X G F ( С f , т f ; С г , Т г )| F _— 0

и для случая, когда начальный сигнал задан как

возмущение в пространстве с законом дисперсии

to ( k ) [16]:

. 8A     1 d ² to ( k ^) 8 ² A

11 8z      2 dk2     8£2 , d to(k0)

С — z --■ t .

dk

где G f ( С f , т f ; С г , т г ) — ФГ радиона в потенциале V ( Q , т ) — - F ( т ) ■ Q . По формуле (44) она может быть вычислена аналитически [20]:

G f ( С f , т f ; С г , т г ) —

2 ■ л^ г ■ ( т f -т г )

x exp

г ■ ( С f -С г )² 2 ■ ( т f -т г )

+ г ■□ F ( С f , т f ; С г , т г )

Если радион излучается радиосистемой в не- однородную изотропную среду с диэлектрической проницаемостью Б(to, x, z), то, выбрав на- пряженность электрического поля в прежнем где добавка к действию свободного радиона за счет переменной внешней силы равна:

gf (С f,т f;С г,т г) — виде (21), получим в приближении квазиоптики

^т f       (

уравнение вида:

— J F ( t ) ■ С f ■

т

-

т г

. 8 A г

8т

-

1 8 2 A

+ V ( С , т ) ■ A , 2 8С 2

т _г

^т f ^-т г

^{+ С} г ■

^т f

- т

^т f ^{- т} г )

■ d т +

отличающееся от уравнения (22) наличием потенциала

^т f ^т f г

₊ 1 f f ( т’-т г ) ■ ( т’’-T г )

^{2 J J} т f ^- т г

Т 1 т i ^{L J}

- min( T‘ - т г , т" - т г )

X

V ( С , t ) — 2 ■

1      to 0       ( с т

¹ -Г2—2 n ^to 0,T,T" k g ■ c     I ^k 0 ^k 0

X F ( т‘ ) ■ F ( т" ) ■ dт' ■ d т" .

.

Свойства радиона в постоянном однородном поле описаны в докладе [21], а для случая

ФГ уравнения (42) также выражается инте- гралом Фейнмана:

Q ( t f ) —С f      _г т f

G ( С f , т f ; С г , т г ) —     J exp г ■ J ( P ■ Q -

^{Q ( т} г ) ^—С г            ^т г                  (44)

- P 2/2 - V ( Q , t )) ■ d т ■ d ц .

Если стационарный потенциал V(С) в (42) — короткодействующий, то по ФГ (44) могут быть найдены коэффициент прохождения D и коэффициент отражения R радиона с импульсом p для этого потенциала [20], а именно, с точно- стью

D ~

R ~

до нормировочного множителя:

lim      G (p ■т f, т f; p ■тг, тг) , т f ^+^,т г ^—ю

^lim       G ^{( -} p ■т f , Т f ; p ■T г , Т г ) .

т f ^+Ю . Т г ^-ГО

Если же потенциал V ( С ) еще и мал, то в этом случае ФГ (44) может быть вычислена по теории возмущений следующим образом [20]:

G ( С f , Т f ; С г , Т г ) —

V ( С , т ) — V 1 ( t ) ■С ² + V 2 ( t ) ■С ,                      (49)

где V 12 ( t ) — произвольные функции, свойства радиона совпадают с свойствами оптического пучка в планарном световоде с показателем преломления среды (49), исследованными в [22; 23].

Если же диэлектрическая проницаемость изотропной среды является гауссовским случайным полем вида:

б ( x , z ) — £■ [1 + Б 1 ( x , z )], (50)

то при предположении о дельта-коррелирован-ности поля Б 1 ( x , z ) вдоль направления распространения волны:

< Б 1 ( x , z ) ■ Б 1 ( x' , z' ) > — 5 ( z - z' ) ■ a ( x - x' ) (51) средняя по статистическому ансамблю амплитуда <  A >  электромагнитной волны вида (21) удовлетворяет уравнению [1]:

8 <  A >

8т

1 8 ² <  A >  - г ■ k 2 ■ a (0)

2     8С ²           8

которое сводится к уравнению (22) для свободного радиона подстановкой:

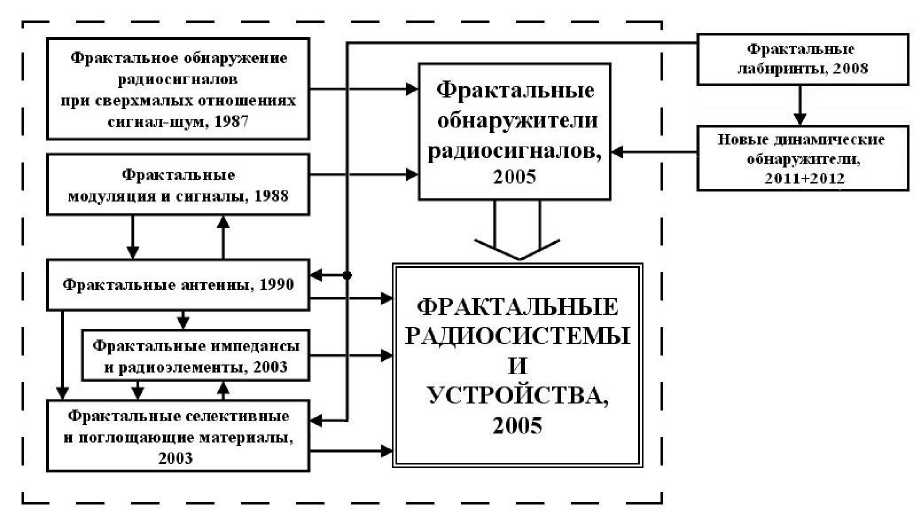
Рис. 3. Концепция А.А. Потапова фрактальных радиосистем и устройств

< A ( £ , т ) >= exp

k 0 ■ a (0) , _т

■ A & т).

Таким образом, случайный характер диэлектрической проницаемости даже упрощает картину по сравнению с детерминированным случаем (46)–(48), приводя только к затуханию свободного радиона. Впрочем, квантовую теорию затухающего радиона на основе подходов Калдиро-лы [24] и Канаи [25] тоже можно построить.

Заключение

• 1.    С помощью интегралов Фейнмана выявлена связь радиотехники, фрактальной парадигмы и квантовой механики. Это привело к введению квазичастицы радиосистем – радиона, свойства которого в одномерном случае выяснены. Перспективой данного исследования является описание свойств двумерных радионов, которые имеют свои характерные особенности по сравнению с одномерными.

• 2.    Подчеркнем качественное отличие нашего тезиса «все радиосистемы – фрактальны» от введенной ранее одним из авторов доклада (А.А. Потаповым) концепции фрактальных радиосистем и устройств – рис. 3 (см. [8–11] и ссылки в них). В рамках этой концепции фрактальные радиосистемы включают в себя фрактальные антенны и цифровые фрактальные обнаружители, основаны на фрактальных методах обработки информации, могут использовать фрактальные методы модуляции и демодуляции радиосигна-

• лов. Другими словами, это – «искусственная», а не «естественная» фрактальность радиосистем. Но, в отличие от «естественно фрактальных» радиосистем фрактальные по Потапову радиосистемы дают весьма существенные преимущества при работе в условиях негауссовых и немарковских шумов и помех при сверхнизких отношениях сигнал/шум [8–11].

• 3.    Математическая подготовка радиоинженеров и радиофизиков отстает от требований времени [26; 27]. Поэтому необходимо вводить в преподавание профильных вузов дополнительные главы функционального анализа, отражающие его современное состояние, в том числе его связи c теорией представлений групп и топологией.