Интегрирование модифицированного уравнения Кортевега - де Фриза с зависящими от времени коэффициентами и с самосогласованным источником

В 1965 г. Н. Забуски и М. Крускал [1], экспериментируя с численным решением уравнения Кортевега — де Фриза (КдФ), открыли солитон и дали ему название. Но действительный «прорыв» произошел в 1967 году, когда американские ученые К. Гарднер, И. Грин, М. Крускал и Р. Миура [2] предложили метод спектрального преобразования, как метод решения задачи Коши для уравнения КдФ. Вскоре после этого П. Лакс [3] показал общий характер этого метода, что очень повлияло на будущие исследования.

Несколько лет спустя В. Е. Захаров и А. Б. Шабат [4] путем нетривиального распространения методов ГГКМ и Лакса смогли решить задачу Коши для другого важного нелинейного эволюционного уравнения, так называемого нелинейного уравнения Шредингера. Тем самым был открыт путь для поиска и открытия некоторых других нелинейных эволюционных уравнений, разрешаемых этим методом.

Вскоре М. Вадати [5] представил метод решения модифицированного уравнения Кор-тевега — де Фриза ut ± 6u2ux + uxxx = 0, встречающегося при решении некоторых задач физики плазмы.

Уравнение мКдФ используется во многих областях, включая альфвеновские волны в бесстолкновительной плазме [6], тонкие упругие стержни [7] и т. д. Существует также много результатов об уравнении мКдФ [8–15] благодаря его простому выражению и богатым физическим приложениям. При поиске точных решений уравнения мКдФ ученые наряду с методом обратной задачи рассеяния использовали также такие методы, как двухлинейный подход Хироты [16], метод коммутации (связи) [17] и др.

Важно также изучение нелинейных волновых уравнений с переменными коэффициентами. Недавно К. Прадхан и П. К. Паниграхи [18] изучили модифицированное уравнение КдФ с переменными коэффициентами u, + a(t)ux - e(t)u2Ux + Y(t)uxxx = 0.

В работе [19] модифицированное уравнение Кортевега — де Фриза (мКдФ) с переменными коэффициентами исследуется с помощью двух подходов и символьных вычислений, а также получены множество типов точных решений с двумя разными бегущими волнообразными переменными.

В данной работе рассматривается следующая система уравнений:

u, + p(t)(6u2Ux + .    + q(t)Ux =2 V V 1 cmk-1 (gk ..■-1-j - gk2gm-1-j) , k=1 j=0

^L(t)g ⁰ = € k g k , ^L(tW _k = ^ k g k ⁺ jg k ^-1 , ^Im ^ k > 0

gk E L2(-ro, to), k = 1,..., N, j = 0,...,mk - 1, где

( dx      ^-u(x,t⁾ A j ( j / .4 j / ,Л ₌      n!

L(t)    iv -u(x,t)     -dx ; ,   gk    Vki(xctt), gk2xEtt)) ,   cn    (n - 1)U!, gk0 = gk01(x,t), gk2(x,t))T — собственная вектор-функция оператора L(t), соответствующая собственному значению ^k (Im^k > 0) кратности mk, k = 1,... ,N, а p(t) и q(t) — заданные непрерывно дифференцируемые функции.

Предполагается, что

∞

7—^—m [ (gmlk-1gk'2k-1-i + gk2k-1gm1k-1-i) dx = Am.-i-i(t).

(mk - 1 - l)! J x7

-∞ где Amk-i-i(t) — изначально заданные непрерывные функции, l = 0,..., mk - 1. Уравнение (1) рассматривается при начальном условии

u(x, 0) = uo(x), x E R.

В рассматриваемой задаче начальная функция u o (x) , —то < x < то , обладает следующими свойствами:

∞ j (1 + |x|) |uo(x)|dx < то.

2) Оператор L(0) = i

-∞ d dx —uo(x)

^U 0 d ^X) | имеет ровно 2N собственных значений dx

£ 1 (0), £ 2 (0),... , £ 2 N (0) с кратностями m i (0),m 2 (0),... , m 2 N (0) и не имеет спектральных особенностей.

Предположим, что функция u(x, t) обладает требуемой гладкостью и достаточно быстро стремится к своим пределам при x → ±∞ , т. е.

+ ∞

-∞

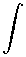
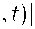
d ^k u(x,t) \ , dx <  dxk    /

Основная цель данной работы — получить представления для решения u(x, t), g j (x, t) , k = 1,..., N, j = 0,..., m k — 1, задачи (1)-(5) в рамках метода обратной задачи рассеяния для оператора L(t) .

2. Необходимые сведения

Рассмотрим систему уравнений Дирака на всей оси ( -∞ < x < ∞ )

J v i x + i£v i = u(x)v 2 , (V 2 x — i£v 2 = —u(x)v i

с потенциалом u(x) , удовлетворяющим условию (4). Видно, что с помощью оператора

d

L = i dx .

—u(x)

—u(x)

- ^d dx

^ и вектор-функций v = (v i ,V 2 ) систему (6) можно переписать в

виде Lv = £v. Система уравнений (6) имеет решений Йоста со следующими асимптоти-

*,£) - ( 0 "; ^(x.«) - ( Д ^0£x > Im £ = 0, x ^—то;

^{0(x,£) -} ( 1 )e^{< x} ; ^0(x,£) ^- ( 0 )^е -^{<0 Im£} = ^0, x ^^то-

Отметим, что ⁰ (0) не является комплексным сопряжением к у (0) .

При действительных ξ пары вектор-функций {ϕ, ϕ} и {ψ, ψ} являются парами линейно независимых решений для системы уравнений (6). Поэтому имеют место следующие соотношения:

У = a(£ )0 + Ь(£)0^ )     0 = — a(£)0 + b(£ >,

0 = -a(£)0 + b(£)0, /,    0 = a(£> + b(£)0,

,                        (8)

где a(£) = W {^,0} , b(£) = W {0, ^} . Верны следующие равенства

^{|a(£ )| 2 + |b(£)|} 2 = ⁰   a^(£ )= a^(—£),   b^(£) = ^b(—£).

Коэффициенты a(£) и b(£) непрерывны при Im £ = 0 и удовлетворяют асимптотическим равенствам

a(£) = 1 + O (|£| ^{- 1}),   b(£) = O (|£| ^{- 1}),   |£|^то.

Невещественные нули {t k } N =i функции a(f) являются собственными значениями оператора L(t) в верхней полуплоскости Im f > 0 . Собственные значения оператора L(t) в нижней полуплоскости Im f <  0 совпадают с нулями функции a(f) . Итак, множество {f k , —f k } N =i является собственными значениями оператора L(t) , и других собственных значений этот оператор не имеет. Требование отсутствия спектральных особенностей несамосопряженного оператора L(0) означает отсутствие действительных нулей у функции a(f ) , т. е. a(f) = 0 , f Е R .

Определение 1. Функции

( s )                d s

^{V (x,f} k ) = dt s V^(x,f)

, s = 1, • • • ,m k — 1, 5 = 5 k

называются присоединенными функциями к собственной функции v(x,f k ) .

Аналогично определяются присоединенные функции к собственной функции ^(x, f k ) .

Собственные и присоединенные функции удовлетворяют уравнениям

( s )                   ( s )                 ( s - i)                (0)

L^V (x,f k )= f k ^V (x,f k )+ s ^V (x,f k ); ^V (x,f k ) = V(x,f k ), k = 1, • • •, N,    s = 0, • • •, m k — 1-

Существует такая цепочка чисел {у ° , X ^k , • • • ,Xm._k - i }, что имеют место соотношения [20]

( l )                                 , l! ( v )

^{V (x,f} k ) = ^2x°-v ^y ^ ^(x,f k ), ^k = ^1,••• ^,N, ¹ = ^0,••• ,m k ^— 1" v =0      V

Последовательность чисел {х о , X k ,•••, Х°п._к - 1} будем называть нормировочной цепочкой оператора L .

Для функции ^(x,f) справедливо (см. [21, с. 33]) следующее интегральное представ ление:

∞

Wx,f) = ( J ) e i ⁵ x + У K (x,s) e i ^€ s ds,

x где K (x,s) = (Ki(x,s),K2(x,s))T. В представлении (9) ядро K (x,y) не зависит от f и имеет место равенство u (x) = —2Ki (x, x) •

Компоненты ядра K (x, у) представлении (9) при y > x являются решениями системы интегральных уравнений Гельфанда — Левитана — Марченко

∞

K 2 (x,y) + У K i (x,s)F(s + y) ds = 0, x

∞

—Ki(x, y) + F(x + у) + У K2(x, s)F(s + y) ds = 0, x где

-.   ^                    N m k - i

F(x) = 2 _n   г ^{+ ( 4}^x df " i^ E X km k - v - i

-ro                   ^k = ^{i v} = ⁰

1 d ^v

V! dz ^v

I' •

f k ) m k e izx' a(z)

]

^, z = ^ k

a(z) — аналитическое продолжение функции a(f) ( Im f = 0 ) в верхнюю полуплоскость Im z > 0 , которое определяется по формуле

a(z) = exp <

∞

— I'

2ni J

-∞

in(i + |r+«)|)

f - z

N

d€}n (H)

m j

.

Теперь потенциал u(x) определяется из равенства (10).

Определение 2. Набор величин

|r+(f), f G R; fk, Imfk > 0; xk, k = 1,---,N, j = 0,...,mk — 1} называется данными рассеяния для системы (6).

Справедлива следующая теорема (см. [22, § 6.2]).

Теорема 1. Данные рассеяния оператора L однозначно определяют L .

Лемма 1. Пусть вектор-функции n(x, f), g k (x, t), s = 0,..., m k — 1, являютсяреше-ниями следующих уравнений:

L^(t)n = ^  ^L(t)g s = ^f k g s ⁺ sg s      s = ^0,...,m k ^{— 1}

тогда справедливы равенства dx (gsin2 — gs2ni) = i(f — fk) (gsin2 + gs2ni) — is (gsi in2 + gs2 ^i) , dX (gsi^i + gS2^2) = —i(f + fk )(gsiVi — gS2^2)

is (gs i ⁱ ^ i ^— g^M,

s = 0, . . . , m k — 1.

Эта лемма доказывается непосредственной проверкой.

Следствие 1. При выполнении условий леммы 1 справедливы следующие равенства:

s gkiVi

s gs2n2 = i ^2

l =0

1 s ^!     d тл Г s-z 1

( f +^ k j +r ( s—1П dXVXg k

а при f = f k

s gsin + gs2^i = 2L

1 =0

i

(f - f k ) l ^{+1 (s}

“TTi dTW Wk¹ ’^} ’ s = ^0,---^,m k ^{— 1},     ⁽¹³⁾

— l) ! dx     Ik J

где V {f, g} = f i g i + / 2 5 2 .

Следствие 2. Справедливы следующие равенства:

(n)/             s-i(n)/            n        (n-1)/                (n-1)/ gki V2(x,fk) + gk2 vi(x,fk) = s I gki ^2 (x,fk) + gk2 n (x,fk))

[4pt] + IdxW{g k , ( ^{n )} (x, f k )}, s = 1, 2,...,m k — 1.

3. Эволюция данных рассеяния

Пусть потенциал u(x, t) в системе уравнений LY = £Y является решением уравнения

Ut + P(t)(Uxxx +6u2Ux) = G(x,t), где

N m _k - 1

^G(x,t) = ^—q^(t)u x ^(x,t)+2 ^ ^ C m к - 1 (g jj i g m ^-1-j k =1 j =0

j  m k - 1 - j

^{- g} k 2 ^g k 2         ^.

Оператор

A = P(t) (

—4iV 3 + 2iu ² ^

—4u£² + 2iU x ^ + 2u³ + U xx

4uV 2 + 2iu _x ^

4iV 3 —

- 2 u ³ 2iu ² ^

-

u xx

удовлетворяет соотношению Лакса

[L, A] = LA — AL = ip(t)   ^

6u ² u _x

-

u _xxx

-6 u ² u _x -0

u xxx

.

Поэтому уравнение (14) можно переписать в виде

L t + [L, A] = iR,

где R = (

- G

— G  0

). Дифференцируя равенство Lp = ^p относительно

t ,

учиты-

вая (16), имеем (L — ^)(pt — Ap) = —iRp. Используя метод вариации постоянных, можно записать pt — Ap = B (x)V + D(x)p.

Тогда для определения B(x) и D(x) получаем

MB x V + MD x p = -Rp,

где M =

-

1 ) . Для решения уравнения (18) вводим следующие обозначения:

p = ( ^ 2 p i ) T , V = ( ^ 2 V 1 ) ^T . Согласно (15) и определению вронскиана справедливы следующие равенства:

V ^T Mp = ~ ^т MV = a, V T MV = p ^T Mp = 0.

Умножая (18) на p^T и V ^T , получаем

B x

⁽’^{T R}p   _п

, D _x a

-

V ^T Rp

a

.

Согласно (15), при x → -∞ имеем

.      / 4iV 3 p(t) \

- iξ x

pt - Ap ^ (    0    ) e поэтому, на основании (17), имеем D (x) ^ 4i^3p(t), B(x) ^ 0 при x ^ —то. Следова- тельно, из (19) можно определить

D(x)

x

= — -J ф^тRydx + 4i^ 3 p(t),

-∞

x

B (x) = 1 / ^a

-∞

yTRy dx.

Таким образом, равенство (17) имеет следующий вид:

xx yt — Ay = — J yTRy dx^ + I — j pRy dx + 4i^3p(t) j y.

-∞             -∞

Предположим, что справедливо равенство

N

M (yi^i + y2^2) = ^(Mk1 + Mk2), k=1

где

N m _k - 1

M = 2 E E cmk-1 (gk 1 ■■-1-j—gk   2-1-j) • k=1 j=0

Сделаем следующие вычисления:

² (g k i g m ^{-1-j —} g k 2 g m ^{k -1-j} ) (M⁺ y 2 ^ 2 )

= 2g j i g m k ^{- i - j} y* — 2g k 2 g m k ^{- i - j} y 2 < 2 — 2g k 2 g m ^{- i - j} y i ^ i + 2g k 1 g m k ^{- i - j} y 2 < 2

= (g k i y i + g k 2 y 2 ) (g m k ^{- i - j} ^ i — g m 2 ^{k - i - j} < 2 ) + (g k i y i — g k 2 y 2 ) (g m ^{k - i - j} ^ i + g m ^{k - i - j} ^ 2 )

⁺ (g k i y 2 ⁺ g k 2 y i ) (gg m k ^{- i - j} ^ 2 ^— g m ^{k -i-j} ^ i ) ⁺ (g k i y 2 ^— g k 2 y i ) (g m ^{k -i-j} ^ 2 ⁺ g m ^{k -i-j} ^ i ) •

Откуда имеем mk-1

^M k i = ^ C m k - i (g j i y i ⁺ g k 2 y2) (g m ^-i-j ^ i ^— g m ^{k -i-j} ^2) j =0

m k - 1

⁺ ^ C m k - i (g k i y i ^— g j 2 y2) (g m ^-i-j ^ i ⁺ g m ^{- i - j} ^2) • j =0

Это равенство, исходя из равенства (13), можно записать в следующем виде:

mk -1                   mk -1-js

C j          j 1            ^{( —}1) i     ^(mk ^{— 1 —j)!} d Г m _k - i - j - s ,1

ki =Ю  mk-i[ {gk,y}  S=0  (e + ^k )s+i (mk — 1 — j — s)! dx VVgk,^l_ mk -1                                j

+ E C m k - i [V{gm k       V (ё^(-^dxV{gk^-.y}].

Легко показать, что в правой части последнего равенства коэффициенты при

V{gk,y}dxV{gk,^} и V{gr,^}dx V{gk,y}, 0 < r + q < mk — 1, одинаковые, поэтому Mki есть линейная комбинация выражений вида -dx (V {f^., ^} V f^, ф}), 0 C r + q ^ mk - 1, т. е. справедливо следующее:

m k - 1 m k - 1 - j     s j

M k 1 = ^{£ £} (-^C m

1 (m k - 1 — j)! d

j =0 s =0

(^ + ^ k ) s ⁺1 (m k —¹ -j — s)! dx

V g k^{m k}

^{1- j - s} ,ψ V g _k ^j ,ϕ   . (22)

Аналогичном образом можно показать справедливость следующего тождества для M _{k 2} :

mk — 1 mk-1—j (-1)siCj mk

M k 2 = E E

1 ( m k - 1 - j )! d

j =0 s =0

(C k — €) ^s+1 (m k — 1 —j — s)! dx

W g k^{m k}

^{1- j - s} ,ψ W g k^j ,ϕ . (23)

Точно так же, если

снова воспользуемся вышеуказанным методом, получим равенство

N

M (ф1 + ф2) = ^£(Hk1 + Ha), k=1

где mk-1 mk -1-j

H k 1 = E E C m.

j =0 s =0

(-1) ^s i     (m k - 1 - j)! d

¹ (€ + ^ k ) ^s+1 (m k - 1 - j - s)! dx

V g k^{m k -1- j - s} ,ϕ V g k^j ,ϕ ,

m _k - 1 m k - 1 - j

H k 2 = E E C m . - 1

j =0 s =0

(-1) ^s i     (m k - 1 - j)!    d

(^ k - €) ^s+1 (m k - 1 - j - s)! dx

W  gkmk-1-j-s, ϕ W  gkj,ϕ   .

n _r           , j              f Ф 1 (x,^) A /     ^1 (x,€) A

Лемма 2. Если вектор-функции ф =      ; Л и 'ф =        J являются

V ф2 (x,0 )         V ^2

решениями уравнения (6) , то для их компонент выполняются равенства

∞

J G (ф г ^ 1 + ф 2 ^ 2 ) dx = 0,

-∞

+∞ j G (ф1 + Ф2) dx = 2i£q(t)a(£)b(£).

-∞

<1 Для доказательства справедливости тождество (24) нам требуется вычислить следующий интеграл:

+∞ j G (ф1^1 + ф2^2) dx =

-∞

+ ∞

+ ∞

-q(t) j U x (y r ^ i + ^ 2 ^ 2 ) dx + j M (y r ^ i + ^ 2 ^ 2 ) dx.

-∞

-∞

Сначала вычислим первый интеграл в правой части последнего равенства. Действительно, используя формулы (5), (6), (7) и (8), можем выполнить следующие вычисления:

+ ∞

-q(t) У и х (ф 1 ^ 1 + Ф 2 ^ 2 ) dx = - _R lim^q(t) [u(x,t)(ф г 0 1 + ф 2 ^ 2 ) ] | R _R

-∞

+ q(t) У U (ф ‘ 1 ^ 1 + ф 1 ^ 1 + Ф 2 Ф 2 + ф 2 ^ 2 ) dx = - R lin ^ q(t) [u(x,t)(ф 1 ^ 1 + ф 2 ^ 2 )]^|£

-

∞

⁺ q(t) j И^(-0 2 ⁺ i00 2 ) + ⁰ 1 (-^ 2 ⁺ i^ ) ⁺ ^ 2 ⁽⁰ 1 ⁺ i€0 1 ) ^{+ 0} 2 (^ 1 ⁺ i€^ 1 )] ^dx

-∞

+ ∞

= - R lim q(t) [u(x, t) (^ 1 0 1 + / 2 0 2 ) ] I RR + i^q(t) j (^ 1 0 2 + ^ 2 0 1 ) ’ dx = 0.

-∞

Теперь нам нужно вычислить интеграл

+∞ j M (^101 + ^202) dx.

-∞

Используя равенства (21), (22) и (23), получим

+∞ j M (^101 + ^202) dx = 0.

-∞

Согласно последним тождествам, мы можем получить следующее равенство:

+∞ j G (^101 + ^202) dx = 0.

-∞

Для доказательства справедливости тождества (25) требуется вычислить интеграл

+ ∞

j G(Vi + ^ 2 ) dx =

-

+ ∞

j q(t)ux{^ 1 + ^ 2 ) dx +

+ ∞

У M (^ 2 + ^ 2 ) dx-

-

CO

-

co

-

co

Сначала вычислим первый интеграл в правой части последнего равенства

-

oo

oo

j q(t)ux (^ 2 + ^ 2 ) dx =

oo

oo

⁺ q^(t) j u (y^:

OO

oo

^-q^(t) У (^ 1 ⁺ ^ 2 ) ^du =

-

q^(t)u (^ 2 ⁺ ^ 2) ¹

OO

oo

oo

oo

+ ^ 2 ) dx = 2q(t) У (u^ ₁ ^ ^/ ₁ + u^ ₂ ^ 2 ) dx

-

oo

= 2q^(t)У [(-^ 2 ⁺ i€^ 2 ) ^ 1 ⁺(^ 1 ⁺ i€^ 1 ) ^ 2 ] ^dx =²i^q^(t) R ^lim⁽^ 1 ^ 2 ^{) |}

R

R

= 2i^q(t)a(C)b(^ ).

-

OO

Справедливость равенства

У M (^ 1 + ^ 2 ) dx

=0

-

OO

показывается так же, как и выше. Таким образом, получим равенство

У G (^ 1 + ^ 2 ) dx

= ²ⁱ£,q⁽t^)a(O^b(O- ▻

-∞

Перейдем к нахождению эволюции нормировочной цепочки {х П ,Х п • • •, X^Tm._k -1} , соответствующей собственному значению £ n , n = 1,...,N. Для этого перепишем равенство (20) в виде

2 . - Аф = -a

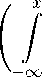
G (ф 1 С 1 + 2 2 ^ 2 ) dx^

x

— / G ( ф !

-∞

⁺ 2 2 ) dx^

+ 4i ^ ³ p(t)y.

Учитывая вид a(^) и равенство (12), получаем

x

x

/                           m k - 1

M k i dxy - / H k i dxC = a(^ ) ">   C m k

-c         -c               i =o

x i / (gm-1-j21

-∞

mk — I - j

^- 9 k 2     2 2 J

^dxg k ,

где g k = j 2 ,

g j 1)

T

. Точно так же, применяя равенство (13), получим равенство

x

x

/                           m k - 1

M k 2 dxy - / H k 2 dx^ = a(^ ) ^ C m _k

-c         -C               j = ^o

x

1 У (g m i k ^{- 1 - j} 2 2 ⁺ g m ^-1-i 2 1 ) dxg k •

-∞

На основании вышеизложенного, равенство (26) можно переписать в следующем виде:

N m k - 1         x

2 . - Аф = E E C m -1 / (g m ^{- 1 -} ‘ 2 i ^k -i i - ⁰        -C

-

mk-1-jm A gk2      22

dx g k

+

a

xx

-q(t) У U x (2 1 C i + 2 2 C 2 ) dxy - q(t) У U x (2 1 + 2 2 ) dx^j

-∞-∞

+ ]ZmE1 Cmk-i / (gmik-i-j22 + gm-1-i2i) dxgk + 4i£3p(i)2. k-1 i-°

Дифференцируя это равенство m n - 1 раз по ^ и полагая ^ = ^ n , получим

( m n ^-1)

∂ ϕ n ∂t

^(m n ^{-1)               (} m n ^{-2)   (m} n ^{- 1)(m} n ^- 2)    ⁽ m n ^-3)

- A o   2 n   -(m n - 1)A i   2 n--

(mn - 1)(mn - 2)(mn - 3) a (mn-4) 6

= R i (x) + R 2 (x)

mn-1

_{i            m - 1 - i} ( m n - 1) _{m - 1 - i} ( m n - 1)                      ( m n - 1)

^C m n - 1 / (5 n 1        2 n 2 +g » 2       2 n 1 )^{d g}g n ⁺⁴ⁱ^ n P^(t) 2 n

3-0       -C V                                ;(27)

+ 12i^ n (m n - 1)p(t) ⁽ 2 n ) +12i^ n (m n - 1)(m » - 2)p(t) ⁽ 2 n 3)

( m n - 4)

+ 4i(m n - 1)(m n - 2)(m n - 3)p(t) 2 n

+ q(t)

( ⁽mn^-1) \            / 0      \

( m„ - i) n     I - ²ⁱ^ ⁿ q^(t) I  ⁽ m n ^-1) )

2 ⁿ 1 n                       ^{2 2} n

-

2i(m _n

-

1)q(t)

( m n - 2)     ^,

2 2 n

где A l =

;fa| ,

^ ^— ^ n

l = 0,1, 2, 3,

N m k - ^{1       X}

R 1 (x) = EE C m . - 1 / (g' k^ - ^1— j Й^{4 k} =1 j = ⁰        —L ^v

-

m_k — 1 — j ^(m n g k 2        S n 2

; 1)) dxg k ,

N mk-1         X /\

R = (x) = E E C m -1 / g ms ^{— 1 — j} ■ ■ + ^—1— j ‘ m-0 dxg k .

k=1, j=0        —L V7

k =1

Заметим, что согласно (12) и (13)

lim R 1 (x) = lim R ₂ (x) = 0.

X^L

Используя следствие 1 леммы 1, можно показать, что mn—1

E c m n —1 / С

7=0

j U

m — 1—j (mn 1)   mk — 1—j ‘mn gn1k       Sn2  +gn2k       Sn1

¹⁾ dx g _n ^j

mn—1

E Cmn—1 /n

7=0

j v

₁ ( m n - 1 - j )    _{m n}

V n 2    ^+g n 2

₁ ( m n - 1 - j ) S n 1 ) dx

mn

- 1

g n + 52 E j ^(x)g n , j =1

где E j (x) есть линейная комбинация выражений вида W^g n_t ,S n } ( r - q = j) , и поэтому ( s )

lim E j (x) = 0. Согласно определению функций д П и s n , s = 0,..., m n — 1 , существуют

X ^L ^J

числа d g , d 1 ,..., d m n

1 такие, что

j j                s          (s)

^g n — / _v ^cj d j — s T n s =0

j = 0,...,m n — 1.

Поэтому мы можем выполнить следующие вычисления:

m n

j =0

x

C ^j m _n

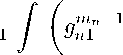
( m n — 1 — j ) T n 2

-L

+g n ^m 2 ⁿ

( m n — 1 — j ) T n 1

)

dx g _n ^j

x

m n - 1

E C m n —1 / С

7=0         J j=      -L

g n ^m 1 ⁿ

^(m n ^—1—j )     m n — 1 ⁽ m n ^—1—j )\    V^          ^(s)

Tn2   +gn2      Tn1    dx C dj-s Tn s=0

m n - 1 m n - 1

=

C ^{j m}

s =0 j = s

x

_jC‘ d j—.j (g m ^{n —1}

-L

( m n - 1 - j ) T n 2

+g n ^m 2 ⁿ

-1

( m n - 1 - j ) T n 1

)

( s ) dx ϕ n

m n - 1         m n - 1 -

= ECm n—1  E s=0            k=0

s

k ^C m n

1 — s

x dmn -1-k-s

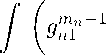
( k )                  ( k )

S n 2 +g _{n 2} n S n 1 I dx

-L

( s ϕ n

m n - 1

=    Cs mn -1

s =0

j (g m

- 1 m n - 1 - s g n 2

m n

+ g _{n 2}

^{— 1 m} n ^—1— s A j (?) g _{n 1}         dx T _n .

Таким образом, согласно (27) равенство (28) можно переписать в виде

⁽ m n ^-1)

∂ ϕ n ∂t

⁽ m n ^{-1)                (} m n ^{- 2)}  (m n ^- l)(m n ^- 2)    ( m n ^{- 3})

- A o V n -(m n - 1)A 1   V n---------- A 2   V n

^(m n ^{- 1)(m} n ^{- 2)(m} n ^{- 3)} A ^(m v ^-4)

m n - 1

= E c s=0

x

/ ( „mn - l „mn - 1 -

Ig n 1     g n 2

-∞

+ - П? g m     '^ dx К + 4i 5 n p(t) "' V„ ‘'

+ 12iC n (m n - l)p(t) ⁽ V n ) +12i^ n (m n - 1)(m n - 2)p(t) ⁽ V n ³ )

_x _ (mn -4)     „     „               •

+ 4i(m n - 1)(m n - 2)(m n - 3)p(t) V n +R 1 (x) + R2M + E Q j ^(xW n j =1

+ q(t)

((mn-1) \             / 0\

(m„ -1)     I - 2i^nq(t) I  (mn-1))

p1n    )           V V2n)

-

2i(m _n

-

1)q(t)

I ( m n - 2) I • 2 n

Используя (5), (2), (27), (28), перейдем в последнем равенстве к переделу при x → ∞ .

Приравнивая коэффициенты при

( 1 } (ix) l • e i^ n x

l = m _n - 1, m _n - 2, • • •, 0 , получаем

следующие обыкновенные дифференциальные уравнения:

n

J⁰ = Si; ³ p(t) - 2 q(t) + A n (t)) x n ,

n

-dt ¹ = (Si^ n p(t) - 2i^ n q(t) + A n (t)) х П + (24i^ n p(t) - 2iq(t) + A n (t)) х П ,

n

X2                           Дп vn 9zU?2T)(tA            An(t^ vn dt  = ysiSnp(t)   2iSnq(t) + A0 (t)) x2 + ^24iSnp(t)   2iq(t) + A1 (t)) x‘

+ (24i^np(t) + An(t)) хП, dll = (Si^np(t) - 2i^nq(t) + An(t)) хП + (24i^np(t) - 2iq(t) + An(t)) хП + (24i^nP(t) + An(t)) ХП + (Sip(t) + An(t)) ХП,

-I n = (Si^ n p(t) - 2i^ n q(t) + A n (t)) x n + (24i^ n p(t) - 2i^ n q(t) + A n (t)) Х П - 1

+ (24i^ n p(t) + A n (t)) Х П - 2 + (Sip(t) + A n (t)) х П - 3 + ;E A n - s (t)x n , s =0

n = 1, 2, • • •, N,    l = 4, 5, • • •, m _n - 1.

Теперь приступим к вычислению эволюций r+(^) и ^j, j = 1,...,N. Согласно (8), равенство (20) можно переписать виде xx at^ + bt^ - A (a^ + b^) = - ^ фтRv dx ^ + ( — У тфтRv -x + 4i ^3p(t) j (a^ + b^) •

-∞             -∞

Переходя в последнем равенстве к пределу при x ^ +^ и учитывая (15), можем вывести следующие равенства:

∞ a t = — У T T R^dx, -∞

∞∞ b t = - [ ipT R^dx — - [ фт R^dx + 8i£ 3 p(t)b.      (30) aa -∞         -∞

Следовательно, при Im £ = 0 можем вывести выражение

∞ dr- =8i^3p(t)r+ - Д2 [ G (^1 + <^) dx.

dta

-∞

Лемма 3. Собственные значения и функция рассеяния оператора L меняются по t следующим образом:

mk(t) = mk(0), :.(t) = :.(0), k = 1,...,N, dr+

"dt- = (8i£3p(t) - 2i£q(t)) r+, Im£ = 0.

• < 1 Согласно равенствам (30) и (24) имеем a t = 0 . Поэтому справедливы следующие выражения: m k (t) = m k (0) , ^ k (t) = ^ k (0) , k = 1,...,N. Учитывая (25), из (31) легко получаем тождество (33). ⊲

Таким образом, доказана следующая теорема.

Теорема 2. Если система функций u(x, t), g jj (x, t), k = 1,..., N, j = 0,..., m k — 1, является решением задачи (1) – (5) , то данные рассеяния несамосопряженного операто ра L(t) с потенциалом u(x,t) удовлетворяют дифференциальным уравнениям (29) , (32) и (33) .

Замечание 1. Полученные равенства полностью определяют эволюцию данных рассеяния, что позволяет применить метод обратной задачи рассеяния для решения задачи (1)–(5).

Пусть задана функция u o (x) , удовлетворяющая условию (4). Тогда решение задачи (1)–(5) находится по следующему алгоритму.

• •    Решаем прямую задачу рассеяния с начальной функцией u o (x) и получаем данные рассеяния

V+ (£, 0) , £ € R; ^k (0), Im ^k > 0; xj (0), k = 1,...,N, j = 0,...,mk — 1 } для оператора L(0).

• •    Используя результаты теоремы 2, находим данные рассеяния при t >  0 :

{r ⁺ (£,t) , £ € R ; ^ (t), Im ^ k > 0; x j (t), k = 1,...,N,j = 0,...,m k — 1}.

• •    Методом, основанным на интегральном уравнении Гельфанда — Левитана — Марченко, решается обратная задача рассеяния, т. е. находим единственную (согласно теореме 1) u(x, t) по данным рассеяния при t > 0 , полученным на предыдущем шаге.

• •    После этого решаем прямую задачу для оператора L(t) с потенциалом u(x, t) и находим функции g _k ^j (x, t) , k = 1, . . . , N , j = 0, 1, . . . , m j — 1.

Приведем пример, иллюстрирующий применение этого алгоритма.

Пример 1. Рассмотрим задачу Коши

U t + p(t)(6u ² U x + u xxx ) + q(t)u x = 2 (g 2i - g^ , <             л                   x            2

Lgi = ^ш; u(x,0) = -ch"2x’ где

p(t) = 1 -

_e - 2 t ( t +4)

q ( t ) = 2 t -

_e - 2 t ( t +4)

+ ∞

У g ii g i2 dx = A 0 (t)

-∞

_e - 8 t - 2 t ²

Нетрудно найти данные рассеяния оператора L(0) : {r ⁺ (0) = 0, € 1 (0) = i, X o (0) = 2i}. Согласно теореме 2, эволюция данных теории рассеяния выглядит следующим образом:

€ 1 (t) = € 1 (0) = i, r + (t) = 0, X 0 (t) = 2ie ^{- 8 t -} 2 t ² .

Следовательно, F (x) = 2e ^-x-8t-2t 2 . Решая систему интегральных уравнений (11), получим

2e — x — y +8 t +2 t ² K ^{1 (x,y)} = i + e — 4 x +16 t +4 t 2 •

Откуда находим решение задачи Коши (34):

2                             e-3x+8t+2t2                           e-x u (x,t) = - ch(2x - 8t - 2t2) ’   g11 (x, t) = 1 + e—4x+16t+4t2 ’   g12(x’ t) = 1 + e—4x+16t+4t2 •

• 4.    Нагруженное уравнение мКФ с источником

В работах А. М. Нахушева [23] дается наиболее общее определение нагруженных уравнений и проводится подробная классификация различных нагруженных уравнений. Среди работ, посвященных нагруженным уравнениям, следует особо отметить работы [24–31].

Перейдем теперь к рассмотрению особого случая уравнения (1), а именно, рассмотрим нагруженное модифицированное уравнение Кортевега — де Фриза с источником:

U t + P(U(X 0 ,t)) (6u 2 U x + U xxx) + Q(u(X 1 ,t))U x

N m k - 1

• -' ЕЕ с ?.» — 1 (g k 1 g m k ^—1— j - g k 2® ^—1— j) • ⁽ ) k =1 j =0

где P (y) и Q(z) полиномы от y и z соответственно. Уравнение (35) не является частным случаем уравнения (1), так как в уравнении (35) коэффициенты зависят от значения решения на многообразии меньшей размерности. Если в задаче (1)–(5) вместо уравнении (1) рассмотрим уравнение (35), то справедлива следующая теорема.

Теорема 3. Если система функций u(x, t) , g k (x, t), k = 1,..., N, j = 0,.. •, m ^ - 1, является решением задачи (35) + (2) - (5) , то данные рассеяния оператора L(t) с потенциалом u(X’t) удовлетворяют следующим дифференциальным уравнениям:

m k (t) = m k (0), € k (t) = € k (0), k = 1,...,N,

— = [8i£ ³ P (u(x o ,t)) - 2i^Q(u(x i ,t))]r + , Im£ = 0, dX n = \< P (u(x o ,t)) - 2< Q u x,t)) + A(t)]x T dX n = '8< P (u(x o ,t)) - 2i,t)) + An(t)]хП + №P(u(xo,t)) - 2iQ(u(xi,t)) + An(t)]xn, dXn = [8i^nP(u(xo,t)) - 2i,t)) + An(t)]хП

+ [2< П P (u(x o ,t)) - 2iQ(u(x i ,t)) + А П ( - ) ] х П + [2< _n P (u(x o ,t)) + A n (t)]х П , dX n = [8i^ n P (u(x o ,t)) - 2i,t)) + АП(-)]хП

+ [24i^ n P (u(x o ,t)) - 2iQ(u(x i ,t)) + A n (t)]x n ■ ^A-< P (u(x o ,t)) + А П (t)]xi + [8iP (u(x o ,t))+ А П ( - ) ] х П , dX n = \,3 P (u(x o ,t)) - 2i,t)) + АП(-)]хП + №P(u(xo,t)) - 2i,t)) + A^xT-i + [24^P(u(xo,t)) + АП(-)]хП-2

+ [8iP(u(x o ,t)) + A T (t)] х П - з + '£ A r — s (t)x T , n = 1,...,N, l = 4,...,m _n - 1. s =0

Рассмотрим два примера, иллюстрирующих справедливость полученных результатов для нагруженного модифицированного уравнения Кортевега — де Фриза с источником.

Пример 2. Рассмотрим задачу Коши

U t + 6u ² U x + U xxx + Y(t)u(0, t)u x = 2 (g 2i - g^) , 2

Lgi = €igi; u(x,0) = —^-, где

+ ∞

, _x    (e^-91 - 2X , Г          ₃           x 1

- 9 t _.

Y^(t) = (— 8—)^ch9t,       gii g i2 ^dx = A 0 ^(t) = 4 e

-∞

Как и в примере 1, данные рассеяния оператора L(0) имеют вид: {r ⁺ (0) = 0, ^ i (0) = i, Х о (О) = 2i}. Согласно теореме 3, имеем ^ 1 (t) = ^ 1 (0) = i , r ⁺ (t) = 0 , x 0 (t) = 2ie^A t ) , где

^(t) = 8t + 2

t j Y(t)u(0,T)

dT + 2

t j a0(t ) dT-

Следовательно, F(x) = 2e ^x+ ^ ^(t) . Решая систему интегральных уравнений (11), можно получить

2_e ^-x- y + ^ ^(t)

K ^{1 (x,y)} = i + e - 4 x +2 ^ ( t ) •

Используя последнее равенство и формулу (10), получаем

u(x,t)      ch (2x - ^(t))"

Если в последнем равенстве подставим x = 0 , то, учитывая (37), имеем следующую задачу:

L ‘_т _ ⁸Y^(t)e^At)         _ч .

^ ^(t) = - 1 ₊ e 2 ^ ( t ) ^{+ 8 + 2A} 0 ^(t), ^(0) = 0.

Учитывая (36), находим решение этой задачи ^(t) = 9t . В результате решение рассматриваемой задачи выражается следующим образом:

2                        e—3x+9t                       e—x u (x,t) = - ch(2x - 9t),   g11 (x,t) = 1 + e—4x+18t’ g12(x,t) = i + e-4x+18t •

Пример 3. Рассмотрим задачу Коши

U t + e(t)u(1, t)(6u ² U x + U xxx ) + Y(t)u(0, t)u x = 2 (g 2i - g^ , 2

Lgi = €igi; u(x,0) = —^y, где

1         1 3t                ch ( ⁷ t ⁺⁸ )

A'№ = 4 e²⁵⁺⁴ , ^e4)2,

Y(t) =

(⁴ + (t + 2) 2 e 2 ³⁺ 4) ch ( 2+ )

8(t + 2) ²

.

Решение данной задачи имеет вид

U (X, t) —--7--------- q7 —1~,

' ’’ ch(2x + 2+) '

g 11 (x, t) =

-3x- e

3 t 2 t +4

- 4 x -

1+e ^x

3 t t +2

g i2 (x,t) =

-

x

- 4 x -

1+e ^x

3 t t +2