Интегрирование по положительной мере со значениями в квазибанаховой решетке

Переса [43], недавние работы Калабуга, Дельгадо, Хуана, Санчеса Переса [12, 20-23, 27], а также указанные в них источники.

Так как многие функциональные пространства являются квазибанаховыми, естественно желание распространить векторное интегрирование на случай меры со значениями в квазибанаховой решетке. Принципиальная трудность состоит в невозможности применить соображения, основанные на двойственности, как это делается в подходах Гельфанда, Петтиса и Льюиса [37, 38]. Санчес Перес и Традасете [45] предложили вариант интеграла типа Бартла — Данфорда — Шварца, не используя двойственный подход. Существенный недостаток этого подхода в том, что в нем отсутствует аналог слабой интегрируемости, он сильно зависит от порядковой непрерывности квазинормы и предполагает, что постоянные функции интегрируемы.

В цикле работ авторов [33-35] намечены три новых подхода: во-первых, развитие «чисто порядкового» интегрирования типа Канторовича — Райта как естественного и полезного двойника «топологического» интегрирования Бартла — Данфорда — Шварца; во-вторых, построение пространства слабо интегрируемых функций с помощью порядковой конструкции, используя, например, область определения наименьшего расширения оператора интегрирования (см. Алипрантис и Бёркиншо [10, теорема 1.30]) или же максимальное квазибанахово расширение (в смысле Абрамовича [1]) пространства интегрируемых функций; в третьих, привлечение к исследованию соответствующих пространств интегрируемых и слабо интегрируемых функций идей и методов теории квазибанаховых пространств (см., Кэлтон [29, 31]).

Цель настоящей статьи — дать краткий обзор упомянутых подходов, а также некоторых недавних результатов об интегрировании по векторной мере и общих теорем о представлении порядково ст-полных векторных решеток и квазибаиаховых решеток.1 Статья организована следующим образом. В § 2 приводится необходимый минимум сведений о квазибанаховых решетках. § 3 содержит набросок теории интегрирования Канторовича — Райта скалярных функций относительно положительной меры со значениями в порядково ст-полной векторной решетке, определенной на 5-кольце множеств. Параллельная теория векторного интегрирования Бартла — Данфорда — Шварца представлена в §4. В §5 вводятся слабо интегрируемые функции относительно положительной векторной меры на основе конструкции наименьшего расширения оператора интегрирования. В § 6 приводятся результаты о представлении порядково ст-полных векторных решеток и квазибанаховых решеток в виде векторной решетки классов эквивалентности интегрируемых или слабо интегрируемых функций по векторной мере.

Используются стандартные обозначения и терминология из теории векторных и банаховых решеток, принятые в книгах Алипрантиса и Бёркиншо [10] и Мейе-Ниберга [42]. Все векторные решетки предполагаются действительными. Знак := обозначает «равняется по определению», a N и R — множества натуральных и действительных чисел соответственно.

• 2.    Квазибанаховы решетки

В этом параграфе представлены краткие сведения о квазибанаховых решетках, в частности, конструкция максимального квазинормированного расширения.

ОПРЕДЕЛЕНИЕ 1. Квазинормированным пространством принято называть пару (X, || • ||). г,тс X — вещественное пли комплекс нос векторное пространство н || • || — квазинорма, т. е. функция из X в R, для которой выполняются условия:

• (1)    ||x|| > 0 для веек x G X i1 ||x|| = 0 тогда ii только тогда, когда x = 0:

• (2)    ||Ax| = |A||x| для веек x G X и A G R:

• (3)    сутпествует 1 6 C G R такое. что ||x + у| 6 C (|x| + |y|) для веек x,y G X.

Если, сверх того, для некоторого 0 < р 6 1 выполняется неравенство

• (4)    ||x + y^p 6 ||x||p + |y|p Для всех x,y G X.

то || • || называют р-норм ой, а (X, || • ||) — р-нормированным пространством.

Наименьшая константа C в (3) называется квазитреуголиной константой, или ква-зитреуголъным мноэюителем, или модулем вогнутости квазинормы.

ОПРЕДЕЛЕНИЕ 2. Говорят, что две квазинормы || • |1 и || • ||₂ эквивалентны, если сутпествует константа A >  1 такая. что A^-1 |x|1 6 |х|₂ 6 A|x|1 для всех x G X.

Из фундаментальной теоремы Аоки — Ролевича следует, что всякая квазинорма || • || эквивалентна р-норме | • | для некоторого 0 < р 6 1 (см. Малигранда [39, теорема 1.2], Пич [8, 6.2.5]). Квазинорма | • | индуцирует метрическую топологию на X; метрику можно определить формулой d(x,y) = ||x — y^p. Именно эта топология имеется в виду, когда говорят о метрической сходимости или сходимости по квазинорме.

ОПРЕДЕЛЕНИЕ 3. Квазибанаховым пространством (р-нормированным пространством ) называют метрически полное квазшюрмнровегшюе (р-иормировашюе) пространство.

Основные результаты теории банаховых пространств такие, как теоремы об открытом отображении и замкнутом графике, справедливы в контексте квазибанаховых пространств, см. Кэлтон [31]. Имеется также вариант критерия полноты Рисса — Фишера, см. Малигранда [39, теорема 1.1].

Определение 4. Квазибанахово (квазинормированное, р-банахово) пространство (X, || • ||) называется квазибанаховой решеткой (соответственно, квазинормированной решеткой, р-банаховой решеткой), если X одновременно является векторной решеткой и квазинорма монотонна в том смысле, что для любых x,y G X неравенство |x| 6 |y| влечет |x| 6 ||y|-

Предложение 1. В любой квазинормированной решетке решеточные операции непрерывны по квазинорме и конус положительных элементов замкнут. Более того, если возрастающая (убывающая) сеть (x_a )_aGA сходится по квазинорме к элементу x G X. то x = sup_aGA x_a (соответствеиио. x = inf _aEA x_a).

Из предложения 1 следует, что пополнение квазинормированной решетки X является квазибанаховой решеткой, содержащей X в качестве векторной подрешетки. Кроме того, имеет место порядковый аналог критерия полноты Рисса — Фишера.

Теорема 1. Пусть X := (X, фЦ) — квазинормированная решетка с квазитреугольной константой C >  1. Равносильны следующие утверждения:

• (1)    X — квазибанахова решетка;

• (2)    для любой последовательности (xk )О=1 в X₊ такой, что 520=1 C^k \\xk | < то, существует P^L 1 xk G X:

• (3)    для любой последоватолыюстп (xk )О= 1 в X₊. для которой РО= 1 C^k ||xk| < то. ОО                    n

существует элемент x G X такой, что x = о- 2=1 =1 xk := sup_nGN 2^_k=1 xk.

Напомним, что последовательность (xn)0= 1 в векторной решетке X называют равномерно сходящейся к элементу x G X, если супчествуют 0 < u G X и последовательность действительных чисел (en))^ такт\ что en ^ 0 11 |xn — х| 6 enu для всех n E N. Как и в банаховой решетке (см. [7, теорема VII.2.1]), метрическая сходимость в квазибанаховой решетке полностью определяется порядком.

Теорема 2. Последовательность (х_п)П=₁ в квазибанаховой решетке X сходится по квазинорме к элементу х E X тогда и только тогда, когда для всякой её подпоследовательности (xnk )))=₁ существует подлоследовательность (xnkl ^р сходящаяся равномерно к х.

Из теоремы 2 следует, что каждый положительный оператор из квазибанаховой решетки в квазинормированную решетку непрерывен, а любые две квазинормы, превращающие векторную решетку в квазибанахову решетку, эквивалентны.

В некоторых вопросах требуется более тесная связь между квазинормой и порядком, чем монотонность, см. ниже определения 5, б и 7.

ОПРЕДЕЛЕНИЕ 5. Квазибанахову решетку (X, Ц • ||) (как и квазинорму Ц • ||) называют порядково непрерывной, если соотношение х_а ^ 0 влечет Цх_аЦ ^ 0 для любой сети (х_а )_а£А в X. Если в этом определении сети заменяются последовательностями, то говорят о порядковой а-непрерывностн.

Теорема 3. Для квазибанаховой решетки X эквивалентны утверждения:

• (1)    X порядково непрерывна;

• (2)    каждая возрастающая порядково ограппчеппая последовательность в X₊ сходится;

• (3)    X порядково а-полпа и порядково а-пепрерывпа.

ОПРЕДЕЛЕНИЕ 6. Говорят, что квазибанахова решетка (X, ЦЛ) обладает слабым свойством Фату, если существует константа K >  0, называемая слабой константой Фату, такая, что для всякой возрастающей сети (х_а), имеющей супремум х E X, выполняется соотношение Цх|| 6 K sup_a ||x_aU• Если в этом определении заменить сети последовательностями, то говорят о слабом а-свойстве Фату. Если, же K = 1, то Цх|| = sup_a Цх_а U и в этом случае говорят, что X обладает свойством Фату или ст-свойством Фату.

ОПРЕДЕЛЕНИЕ 7. Квазинормированная решетка (X, U • U) обладает свойством Леви (а-своиством ЛевД. если существует sup_a х_а (соответственно supn xn) для каждой возрастающей сети (х_а) (соответствеппо. последовательности (xn)) в X₊ при условии, что sup_a Цх_аU < го (соответствеппо. supn |xnU < го).

Каждая квазинормированная решетка со свойством Леви является порядково полной квазибанаховой решеткой со слабым свойством Фату.

В следующем определении порядково полную квазинормированную решетку X отождествляем с порядково плотным идеалом в ее универсальном пополнении Xu.

ОПРЕДЕЛЕНИЕ 8. Максимальным квазинормированным расширением порядково полной квазинормированной решетки (X, U • U) называют пару (X^к, Ц • ||_к), где

\\х\\_к ^:= sup {UxU : х E X, 0 6 х 6 |х|} (х E X ^u);

X^к:= {х E X^u : Ик < го}.

Легко видеть, что U • U_K : X^к ^ R — квазинорма с той же квазитреугольной константой C. что л у U • U- Более того. Ц • U_K Лё й^ст p-нормой, ес-ли такова, Ц • ||.

Предложение 2. Если X — порядково полная квазинормированная решетка, то имеют место утверждения: (а) X^к обладает свойством Леви в том и только в том случае, когда X обладает слабым свойством Фату; (б) если X обладает слабым свойством Фату то X^к обладает свойствами Леви и Фату.

ОПРЕДЕЛЕНИЕ 9. Квазинормированную решетку X называют интервалвно полной, если каждый порядковый интервал в X полон, т. е. каждая порядково ограниченная последовательность Коши в X сходится к элементу X.

Теорема 4. Максимальное квазинормированное расширение ( X^к, || • ^_к ) порядково полной квазинормированной решетки ( X, || • ||х) со слабым п-свойством Фату есть квазибанахова решетка тогда и только тогда, когда X интервально полна.

Замечание 1. Выдающийся вклад в геометрическую теорию квазибанаховых пространств внес Кэлтон, см. обзоры [28, 29, 31]. В частности, систематическое изучение квазибанаховых решеток начинается с работы Кэлтона [29], см. также Куартеро и Триана [13], Шульга [51]. Максимальное нормированное расширение нормированной решетки, а также соответствующий вариант теоремы 4 принадлежат Абрамовичу [1, определение на с. 8 и теорема 3]. В этом случае теорема 4 верна без предположения о слабом ст-свойстве Фату. Нам неизвестно можно ли опустить это условие в общем случае. Максимальное квазинормированное расширение X ^к можно определить и в той ситуации, когда X не обязательно порядково полна. Полное изложение материала данного параграфа см. в [35].

• 3.    Интеграл Канторовича — Райта

Интегрирование относительно меры со значениями в векторной решетке имеет свои корни в спектральной теории, в представлении линейных операторов с помощью интеграла по спектральной мере. Теория порядкового интеграла действительных функций относительно счетно аддитивных векторных мер со значениями в порядково полной векторной решетке была развита Канторовичем [3, 4]. Решающий вклад в эту теорию внес Райт [49, 50]. Существующая литература не очень обширна; некоторые аспекты теории отражены в книге [5, гл. 6]. В этом параграфе мы коротко приведем конструкцию и некоторые свойства интеграла Канторовича — Райта для положительных векторных мер. Подробности можно найти в [33].

Пусть X — порядково ст-полпая векто}:шая решетка. П — непустое множество II P (П) — семейство всех подмножеств П. Колвдом (подмножеств П) называется подсемейство R С P (П) такое. что A\ B Е R i1 A U B Е R для всех A, B Е R. ;г б-колвир — это кольцо, замкнутое относительно счетных пересечений. Пусть R^loc обозначает семейство подмножеств A С П такое. что A П B Е R для всех B Е R:

R^с := {A Е P (П) : A П B Е R для всех B Е R }.            (3.1)

Если R — 5-ко.тьпо. то семейство R^luC яв.тястся ст-а.тгеброй ii R С R^luC.

ОПРЕДЕЛЕНИЕ 10. Функция д : R ^ X₊ называется мерой, если д ( 0 ) = 0 и для каждой последовательности (A_n)n=₁ попарно непересекающихся множеств An Е R такой. что U~₌₁ An Е R. ря,т ^=2=1 ^ ( An ) порядково схощстоя к элементу д (и 2=1 An): символически, ∞       ∞        ∞ n

U A n) = o-£^( An ):=V (E^( Ak ) n=1   '      n=1          n=1 k=1

Тройку (П , R , д ) называют пространством с векторной мерой, если П — непустое множество. R — 5-ко.тьпо по,тмножеств П ii д : R ^ X₊ мера.

Определение 11. Говорят, что множество A Е R^loc пренебрелсимо (или, более точно. д-прснеб^ m-oichmo). ее ли д ( B П A ) = 0 для всех B Е R.

Скажем. что свойство P (•) выполняется я.тя почти всех ш Е И пли почти всюду (коротко д-п.в.) па И. если миожество {ш Е И : P (ш) не выпе>лиястся} д-преиебрежимо. Мы можем предполагать, не ограничивая общность, что 5-кольцо R содержит все пре-небрежимые множества и д(A) = 0 для любого пренебрежимого множества A Е R^loc. Подмножество A С И копреиебрео1симо. если И \ A пренебрежимо.

ОПРЕДЕЛЕНИЕ 12. Функция f : И ^ R называется R-простой, если она допускает представление f = ^2П₌₁ akXA_k, ^гД^{е мн}ожества Ai,..., An Е R попарно не пересекаются л ai,..., an Е R (полагаем по (определению Хи = 0).

Множество S(R ) вс ок R-простых функций является векторной решеткой. Для R- простой функции f = n=1a_k a_kXAk определим интеграл J fdд по формуле

n

i;o (f ):= у

f dд := ^ak д(Ak).

k =i

Определение 13. Будем говорить, что R^loc-H3MepHMaH действительная функция f, определенная на копренебрежимом подмножестве И, интегрируема, если существует последовательность (f_n)n=₁ R-простых функций такая, что 0 6 f_n f f д-п.в. и \/^=1 / f_ndд существует в Х₊. В этом случае положим по определению

∞

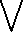
f n dµ.

n =i

Io ^(f) ^:= у f ^dд ^:= o-J ^{f d}Д ^:=

Произвольная R^’-iiBMepiiMtin функция f интегрируема, если таковы f⁺ 11 f^-. Интеграл функции f определяется формулой I°(f) = I°(f ⁺ ) — I° (f^-). Легко показать, что интеграл Io корректно определен, см. [33, лемма 2.10].

Обозначим через L ⁰(д) := L ⁰(И, R Дд) множество всех действительных R^luC-n3-меримых функций, определенных на копренебрежимых подмножествах И. Скажем, что две функции f, g Е L ⁰(д) эквивалентны ii будем писать f ~ g. если f(ш) = д(ш) для д-почти всех ш Е И. Пусть L⁰(д): = L⁰(И,R^10с,д) обозначает множество классов эквива-лептиостп в L ⁰(д) по опк)шешпо ~. Для функщш f Е L ⁰(д) символом f обозначается соответствующий класс эквивалентности в L⁰(д). Линейная структура и упорядочение в L⁰(д) определяются обычным образом, используя поточечные операции и отношение порядка, см. Фремлин [25, §241].

Пусть L1-(p):= L (И, R ^,с, д) — часть L ⁰(д). состояшая из д-иитсгрируемых <]>уик-ций. Символом L0(д):= L¹(И,R^10с,д) обозначим множество всех классов эквивалентности <]>yiiKiiini из Lq(p). Определилi оператор Io : L0(д) ^ X по <]>ормуле Io(f) := Io(f) для всех f Е LO (д).

Определение 14. Говорят, что мера д : R ^ Х₊ локализуема, если для любого семейства A С R^loc существует B Е R^loc такой, что (i) A \ B д-пренебрежимо для всех A Е A ii (ii) если C Е R^luC ii A \ C д-преиебрежимо для всех A Е A. то B \ C также д-преиебрежимо.

Предложение 3. Справедливы следующие утверждения:

• (1)    L⁰(д) поря/ уково a-полная векторная решетка;

• (2)    L¹(д) порядково плотный идеал в L⁰(д);

• (3)    L⁰(д) по])ядково полна топа и только тогда, когда мера д локализуема.

• 4.    Интеграл Бартла — Данфорда — Шварца

Теоремы о сходимости из теории интеграла Лебега также верны для интеграла Канторовича — Райта. Доказательство следующей теоремы может быть проведено рассуждениями, приведенными в [49, предложение 3.3] и [5, теорма 6.1.4].

Теорема 5. Пусть X — порядково a-полная векторная решетка пр : R ^ X₊ — мера. Тогда L0(p) поря,тково a-полная векторная решетка , а 1° строго положите'явный порядково a-непрерывный линейный оператор из L°(p) в X.

Замечание 2. Райт изучал в [49] интегрирование относительно ст-аддитивной меры р со значениями в X U {то}. определешюй на ст-алгеире. Бел и положить R := {A G Б : р(А) G X}, то R будет 5-кольцом, а ограничение р нa R — мерой в смысле определения 10. Интегрируемая по Райту функция будет интегрируемой в смысле определения 13, но обратное, вообще говоря, неверно.

Замечание 3. Райт в [49, теорема 4.1] установил следующий вариант теоремы Рисса о представлении: для линейного положительного оператора T из пространства непрерывных функций C(K ) па колшакте K в порядково полную векторную решетку X существует единственная порядково ограниченная счетно аддитивная квазирегулярная мера р : Boi(K ) ^ X+ такалI. что T(f ) = o-J_K f dp для всех f G C(K ). Квазирсм(лярностъ р означает, что условие регулярности p(F ) = inf {р(и ) : U открыто, F С U } выполняется лишь для зггмкпутых F С K.

Замечание 4. Свойства пространства L0(p) изучены недостаточно. В [5, теорема 6.1.10] показано, что L¹(p) будет порядково полной векторной решеткой, а 1° : L1 (р) ^ X оператором Магарам, тогда и только тогда, когда мера р : R ^ X является наполненной (определение см. в [5, 6.1.9] и [50, определение 3.1]). Отсюда следует, что для наполненной меры имеет место теорема Радона — Никодима [5, теорема 6.1.11 (2)], установленная Райтом в [50, теорема 4.1]; в частности, векторная решетка L°^) реше-топио изоморфна полосе р^^. см. [5. 6.1.11(3)].

ЗАМЕЧАНИЕ 5. Еще одно важное приложение обнаружил Хейдон [26, теорема 6Н]: любая инъективная банахова решетка X линейно изометрична и решеточно изоморфна Ьо(р) для наполненной положительной локализуемой меры р со значениями в порядково полном AM-пространстве с епшищей. если ощхяелптв норму kf k := ||Io(|f|)k^ (f G L0(p')Y Булевозначный подход см. в [6, теорема 4.4]

Бартл, Данфорд и Шварц [И] ввели интегрирование относительно ст-аддитивной векторной меры, определенной на ст-алгебре множеств со значениями в произвольном банаховом пространстве (см. монографию Данфорда и Шварца [2, гл. IV, § 10]). Позднее, Люис [37] предложил альтернативный подход, основанный на теории двойственности. В работах Люиса [38], Масани и Ниеми [40, 41] теория была распространена на векторные меры, определенные на 5-кольцах множеств. В книге Клюванека и Ноулза [32] изучалось пространство L¹(p) для меры р со значениями в локально выпуклом пространстве. Теория интегрирования скалярных измеримых функций относительно меры со значениями в произвольном F-пространстве была развита в работах Волевича [44, §111.6], Турпина [47] и [48, гл. 7], Томаса [46].

В этом параграфе рассмотрим интегрирование типа Бартла — Данфорда — Шварца относительно положительной меры со значениями в квазибанаховой решетке, определенной на 5-кольце множеств. Подробное изложение имеется в работе [34], расширяющей теорию интегрирования, которую предложили Санчес Перес и Традасете в [45]. Как и в § 3. П — непустое множество. R — 5-ко.тьпо по,тмиожеств П. R^loC — ст-алгебра. определенная формулой (3.1), и X := (X, || • |) — квазибанахова решетка.

Определение 15. Отображение д : R ^ X₊ называется мерой (или т-мерой), если д(0) = 0 и для любой последовательности (А_п)П=1 попарно непересекающихся множеств An G R такой, что U^i An G R, Р^яД 52^=1 д (An) топологически сходится и выполняется

∞∞

U An = £д(Ап).

(4.1)

n=1       n=1

Будем говорить, что (Q, R , д) — т-измеримое прослпранство. если Q — непустое множество. R — 5-ко.тыю по,дмиожеств Q. ii д : R ^ X₊ — т-мера. Будем опускать т. если из контекста ясно о какой мере идет речь (ср. определение 10).

Замечание 6. Таким образом, если X — порядково ст-полная квазибанахова решетка, то ст-аддитивность меры со значениями в X имеет двоякий смысл: ряд в (4.1) либо порядково сходится в соответствии с определением 10, либо сходится топологически в соответствии с определением 15, причем сходимость безусловная ввиду положи-телыюстп д. Из предложеиня 1 следует, что т<отологическая ст-аддитивность влечет порядковую ст-аддитивность. Разумеется, если квазинорма в X порядково непрерывна, то эти два разных понятия ст-аддитивности совпадают. В этом параграфе мера понимается в соответствии с определением 15.

Определение 16. Для данной меры д : R ^ X₊ д-пренебрежимые множества, векторная решетка простых функций S(R) и интегральный оператор I^ : S(R) ^ X определяются в точности так же, как и в определениях 11 и 12.

Определение 17. Скажем, что R^loc-H3MepnMaH действительная функция f, определенная на копренебрежимом подмножестве Q, интегрируема, если существует последовательность (fn)n=₁ R-простых фупкпий такая, что 0 6 fn f f д-п.в. и существует limn f nd dд в (X, || • II). В этом случае обозначим

IT (f ):= т-j

f dд := lim n

fn dµ.

Определенная д-п. в. R'^’-iiSMepiiM;гя функция f интегрируема, если таковы f⁺ 11 f^-. При этом полагаем по определению I^T(f):= I^T(f⁺) — I^T(f^-).

Можно показать, что IT(f) корректно определен, т. е. не зависит от выбора возрастающей последовательности простых функций, сходящихся к f д-п.в.

В контексте определения 17 множество L ⁰(д), отношение эквивалентности ~ и порядково ст-полная векторная решетка L⁰(д) имеют тот же смысл, что и в параграфе 3. Пусть ^1(д) обозначает подмножество L ⁰ (д), состоящее из топологически интегрируемых функций. a L1 (д) — множество классов эквивалснтпостп функций из ^^(д). Метко видеть, что оператор топологического интегрирования I^T : f ^ J f dд, действующий из L1.(д) в X. линеен ii строго положителен. Последнее означает, что оператор I^T положителен и равенство I^T(|f |) = 0 влечет f = 0 д-п.в.

Замечание 7. Пусть X — порядково ст-полная квазибанахова решетка. Зафиксируем т-меру д : R ^ X₊. Если функция f интегрируема в смысле определения 17, то согласно предложению 1 f также интегрируема в смысле определения 13 ii I^T (f) = Io(f). В то же время, для данной функции f G L-¹^) ее классы экви валентности в ^^(д) и ^1(д) совпадают. Следовательно, L1. (д) можно считать векторной подрешеткой ^1(д).

ОПРЕДЕЛЕНИЕ 18. Пространством топологически интегрируемых (или, к ороче, т-ин-тегрируемих ) функций называется векторная решетка L1.(д), наделенная квазинормой

If It := Ii; (|f|)|x =

|f | dµ

X

(f G LT (д)).

Из линейности и строгой положительности Г^ следует, что || • ||т есть квазинорма с квазитреугольной константой, не превосходящей такой же константы для || • ||.

Теорема 6. Квазинормиров анное пространство (Ь^(р), || • |_т) является супер порядково полной порядково непрерывной квазибанаховой решеткой и порядково плотным идеалом в Ь°(р). Интегральный оператор Г^ из L1 (р) в X порядково непрерывен и строго положителен.

ОПРЕДЕЛЕНИЕ 19. Пространством порядково интегрируемых (или, к ороче, о-пптег-рируемых ) функций называется векторная решетка Ь1(р) с квазинормой

If Io := К (If|)|x "= ll J If I dp

X

(f 6 LO(P)).

Из линейности и строгой положительности Io следует, что ф |_о есть квазинорма с квазитреугольной константой, не превосходящей такой же константы для | • |. В следующей теореме собраны некоторые важные свойства пространств Ь1(р) и L1 (р)

Теорема 7. Пусть X — порядково a-полная квазибанахова решетка с квазитреугольной константой C. Тогда справедливы следующие утверждения:

• (1)    LO(р) порядково пд<атпый идеал в L°(Q, R ^,с,р):

• (2)    (LO(р), || • ||_о) поря/ уково a-полная квазибанахова решетка с квазитреугольной константой, не превосходящей C;

• (3)    если X р-нормируема для некоторого 0 < р 6 1, то и LO (р) р-нормируема;

• (4)    (L1 (р), ||-||_т) порядково супер порядково полная непрерывная квазибанахова подрешетка и порядково плотный идеал в (Ь0(р), || • |_о);

• (5)    ее.тп X порядково непрерывна. то L(р) = L1. (р) ii Io = Г^.

• 5.    Слабо интегрируемые функции

ЗАМЕЧАНИЕ 8. Бартл, Данфорд и Шварц [11] установили вариант теоремы Рисса о представлении для линейных ограниченных операторов из C(K ) в банахово пространство X: для любого слабо компактного линейного оператор T : C(K ) ^ X существует единственная счетно аддитивная мера р : Bor(K ) ^ X такая, что Tf = I^T(f) для всех f 6 C(K ). Более общие результаты получены Томасом и Кэльтоном, см. [30, введение и теорема 4.3].

ЗАМЕЧАНИЕ 9. Важное и интересное направление приложений векторного интегрирования связано с существованием оптимальной области оператора. Для оператора из некоторого класса, действующего между функциональными пространствами, максимальное пространство (оптимальная область), на которую может быть распространен оператор при сохранении класса и образа, часто представляется в виде L1 (р), г де р — векторная мера, связанная с этим оператором, см. Окада, Риккер и Санчес Перес [43]. Здесь наряду с L1 (р) полезно использовать Ь1(р).

В контексте банаховых решеток ключевую роль играют пространства Ь1(р) и LW (р) соответственно интегрируемых и слабо интегрируемых функций относительно векторной меры р, см. Курбера [15], Курбера и Риккер [16], Дельгадо и Хуан [21], Калабуг, Дельгадо, Хуан и Санчес Перес [12]. Пространства Ь1(р) и LW(р) служат порядково плотными идеалами в Ь0(р); более того, они банаховы, причем L1 (р) — замкнутое подпространство LW(p) (см- Масани и Ниеми [41, теоремы 4.5, 4.7, 4.10]).

Работая с векторными решетками или квазибанаховыми решетками, определение LW(д), основанное на двойственности, более не применимо, но естественной кандидатурой на ролв пространства слабо интегрируемых функций служит область определения наименьшего расширения оператора интегрирования.

Пусть E. F — векторные решетки. F порядково полна ii G — порядковый идеал в E. Рассмотрим положительный оператор S : G ^ F и обозначим через G совокупность всех x Е E таких, что множество {S(g) : g Е G, 0 6 g 6 |x|} порядково ограиинено в F. Тогда G порядково плотный идеал в E и можем положить по определению

Six := sup {Sg : g Е G, 0 6 g 6 x} := sup {S(g Л x) : g Е G} (x Е G+).

Оператор S : G + ^ F аддитивный и положительно однородный, следовательно, он может быть продолжен разностями на все G. Полученный оператор, который обозначим снова через S, продолжает S и не превосходит любого другого положительного продолжения S на. G.

ОПРЕДЕЛЕНИЕ 20. Оператор S называется наймемъшим 2асширением² S относительно E, см. [10, теорема 1.30] и [5, 3.1.3].

Введем теперь две новые квазинормированные решетки слабо интегрируемых функций. Для данной векторной меры д : R ^ X₊, г де X — порядково полная квазибанахова решетка, применим определение 20 для E := L0(д), F := X, G := L0(д) и S := 1°. Обозначим теперь I° := S и L1w (д) := Low (Q, R ^с,д) := G и заметим, что L¹(д) С L°w (д) С L⁰(д). Аналогично, обозначим через Г^ наименьшее расширение оператора топологического интегрирования 1^, и пусть L1w (д):= L1w (Q, R ^с,д) — область определения Г^.

ОПРЕДЕЛЕНИЕ 21. Векторную решетку LOw(д) назовем пространством слабо а-ин-тегрируемих функций относительно д. Снабдим L1w(д) квазинормой kfkow := ^I°o(IfI)^X (f Е L°w(д)) . (5.1)

Определение 22. Пространство слабо т-интегрируемых функций определим как векторную решетку LTw(д), наделенную квазинормой kf IU :=K(IfI)^X (f Е LTwM) .                      (5.2)

В следующей теореме приведены некоторые важные свойства L1_w (д) и L1_w (д).

Теорема 8. Пусть X := (X, || • ||х) — порядково полная квазибанахова решетка с квазитреутольной константой C. Тогда справедливы следующие утверждения:

• (1)    L1_w (д) 11 Low (д) порядково плотпыс идеалы в L⁰(д):

• (2)    LTw (д) и L1_w(д) квазибанаховы решетки с квазитреутольной константой, не превосходящей C:

• (3)    ес ли X p-нормируема для некоторого 0 < p 6 1, то та ковы LT_w(д) и L1w (д);

• (4)    L1_w(д) порядково плотный идеал в L1_w (д) и 1^ 6 Io;

• (5)    интегральньш оператор 1° : L0(д) ^ X порядково непрерывен тогда и только тогда, когда L°w ⁽д) = LTw ⁽д) 11 Io = IT-

• ЗАМЕЧАНИЕ 10. Другая возможность введения слабо интегрируемых функций связана с понятием максимального квазинормированного расширения. Пусть X — порядково полная квазинормированная решетка и (Q,R10с,р) — пространство с векторной мерой р : R ^ X+, локализуемой в смысле [25]. В зависимости от контекста будем считать, что р счетно аддитивна в смысле порядковой или метрической сходимости. Из теоремы 8(1, 4) и предложения 3(3) следует, что L0(р) служит универсальным пополнением каждой из квазибанаховых решеток L°(р) и L1 (р) В соответствии с определением 8 можно построить максимальное квазинормированные расширения (L1K(р), || • ||oк) ii (L1K(р), || • |тк) квазшюрмировапных решеток L0(р) 11 LT(р) соответствешю. В силу теорем 4 и 6 LTK(р) — квазибанахова решетка, в то время как L1K(р) — квазинормированная решетка, которая метрически полна при том дополнительном предположении, что L1(р) обладает слабым ст-свойством Фату. Более того, L1K(р) обладает свойствами Фату и Леви ввиду предложения 2, так как L1 (р) порядково непрерывна. Некоторые свойства квазинормированных решеток L°K(р) и L^(р) рассмотрены в [35]. Детальное исследование этих функциональных решеток представляется весьма перспективным.

• 6.    Представление квазибанаховых решеток

Важно знать при каких условиях произвольная квазибанахова решетка порядково изометрично квазибанаховому функциональному пространству. Различные аспекты данной проблемы изучались многими авторами. Последние достижения связаны с интегрированием по векторной мере.

В этом параграфе покажем, что порядковый интеграл позволяет установить общий результат о представлении произвольных порядково полных квазибанаховых решеток. Ниже X := (X, || • |) — nopiтдково ст-по.тиая квазпиаиахова, решетка и (Q, R, р) — пространство с векторной мерой р : R ^ X₊.

Определение 23. Говорят, что дизъюнктное множество Г с X₊ полно, если X = Г^. Для данного полного дизъюнктного семейства ненулевых положительных элементов из X. определим Xr по формуле

Xr := {x € X : (3 v : N ^ Г) |x| = \/ nv(n) |x1} , где nY — порядковый проектор в X на полосу XY := {y}±±-

Ясно, что Xr — порядково п.тотиыи идеал в X ввиду вклточеыия Г с Xr- Сформулируем теперь два, результата, о представлении.

Теорема 9. Пусть X — порядково ст-полная векторная решетка и Г — полное дизъюнктное подмножество X. Тогда существует прострапство с векторной мерой (Q, R, р) такое, что интегральный оператор 1° является решеточным изоморфизмом из Е°(р') па Xr- Есмп X порядково полна, то мерса р локализуема и наименьшее расширение 1° оператора 1° относительно L⁰(р) есть решеточны й изоморфизм из L°w (р) на X.

Теорема 10. Пусть X — порядково полная квазибанахова решетка. Тогда существует пространство (Q, R, р) с .токалиш'мой мерой р : R ^ X₊ такое, что наименьшее расширение 1° интегрально го оператора 1° устанавливает изометричный решеточный изоморфизм из L^ (Q, R^10срд) на X. Более того, для каждого полного дизъюнктного множества Г С X₊ меру р можно выбрать так, что 1° отображает L1(Q, R^10срд) нa Xr.

Согласно замечаниям б и 7, теории порядкового и топологического интегралов относительно векторной меры совпадают, когда, мера, принимает свои значения в порядково непрерывной квазибанаховой решетке. Ниже рассмотрим частный случай меры со значениями в порядково непрерывной части квазибанаховой решетки.

ОПРЕДЕЛЕНИЕ 24. Порядково непрерывной частью Xan квазибанаховой решетки X называется наибольший порядково непрерывный идеал в X или, более точно, совокупность всех x G X таких, что д.тя данной сети (х_а) в X из cooti юшения |x| >  x_a ^ 0 следует kx_a || ^ 0. Порядково а-пепрерывпая часть Xa квазибанаховой решетки X определяется аналогично, как наибольший порядково а-непрерывный идеал в X, т. е. используя последовательности вместо сетей.

В следующем предложении собраны свойства порядково непрерывной части.

Предложение 4. Для квазибанаховой решетки X верны утверждения:

• (1)    Xa замкнутая подрешетка X и, в частности, Xa — квазибанахова решетка;

• (2)    Xan С Xa. а еели X порядково а-полпа. то Xa = Xan:

• (3)    ее.тп X порядково а-полпа. то для т-измеримого пространства (Q, R, р") с X+-значнoй мерой справедливы равенства

[L1(Q, R¹⁰^a = [L1(Q, R¹⁰",^_an = LT (Q, R¹⁰ Y)Y

Теорема 11. Пусть X — порядково полная квазибанахова решетка, порядково непрерывная часть которой Xa порядково плотна в X. Тогда существует т-нзмернмое пространство (Q, R , р) с локализуемой мерой р : R ^ Xa такое, что интегральный оператор Г^ является изометрическим реснеточным изоморфизмом из LI (р) иа Xa. а его наименьшее расширение Г^ — изометрическим решет очным изоморфизмом из LT_w(р) па X. Более того. L1 (р) = L1(p) iс L1 (р) = L1 (р). а тсжже ГT = Г0 iс ГT = Г0. τ        o       τw        ow

ЗАМЕЧАНИЕ 11. История теоремы 11 начинается с результата, полученного в работе Курбера [15, теорема 8]: всякая порядково непрерывная банахова решетка, со слабой порядковой единицей изометрично и решеточно изоморфна L¹ (р) для некоторой векторной меры р, определенной на а-алгебре. Этот же автор в своей диссертации [14, с. 22-23] сформулировал утверждение о том, что упомянутый результат верен и для банаховой решетки без слабой порядковой единицы, но для этого необходимо распространить теорию интегрирования на векторные меры, определенных на 5-кольцах. В [14] доказательство лишь намечено; детальное обоснование приведено в работе Дельгадо и Хуана [21, теорема 5]. Обобщение в другом направлении получили Курбера и Риккер [16, теорема 2.5]: банахова решетка с а-свойством Фату и со слабой порядковой единицей, принадлежащей ее порядково а-пепрерывпой части, представима в виде банаховой решетки LW(р) слабо интегрируемых функций по векторной мере р, определенной на а-алгебре. Как установлено в работе Дельгадо и Хуана [21, теорема 10], этот результат также остается в силе, если опустить предположение о наличии слабой порядковой единицы, причем вновь приходится привлекать векторные меры определенные на 5-кольцах, см. также Дельгадо [19] и Калабуг, Дельгадо, Хуан и Санчес Перес [12]. Следующий принципиальных шаг сделали Санечес Перес и Традасете [45, теорема 4.3], распространив результат Курбера [15, теорема 8] на квазибанаховы решетки со слабой порядковой единицей. Теорема 11 завершает эту цепочку обобщений, см. [34, теорема 6.7].

Замечание 12. Теорема 11 является новым результатом даже в контексте банаховых решеток. Можно показать, что LT(р) совпадает с пространством L1 (р) всех интегрируемых функций, в то время как L1w(р) содержится в пространстве LW(р) всех слабо интегрируемых функций. Если банахова решетка обладает свойствами Фату и Леви3, то L1w(p) = LW(р) и из теоремы 11 получаем результат Калабуга, Дельгадо, Хуан и Санчеса Переса [12, §6], а также Дельгадо и Хуана [21, теоремы 5 и 9].