Интегрируемость предельной модели плоского вакуумного диода и решение сингулярной краевой задачи

Для модели вакуумного диода изучается сингулярная краевая задача. Обоснована интегрируемость рассматриваемой системы нелинейных дифференциальных уравнений и построена полная система первых интегралов. Разработан метод решения сингулярной краевой задачи, предложены формулы для приближенного решения в окрестности сингулярной точки.

1. Описание модели и постановка задачи. Предельная модель плоского вакуумного диода была получена в [2] группой математиков Тулузского университета. Эта модель представляет собой систему двух нелинейных обыкновенных дифференциальных уравнений второго порядка следующего вида:

^ ² ф    .        (1 + ф )

—2 = 1 I              , dx     V(i+ф)2 - а2 -1

л 2„ u ^            Q dx2      (1 + ф)2 - й2 - 1

ласти

Здесь независимая переменная х е [0,1] означает относительное расстояние от катода, д = 1 соответствует аноду. Функция ф(х) описывает изменение потенциала элек трического поля при перемещении от катода к аноду, соответственно функция а(х) —потенциал магнитного поля; / — плотность тока через диод (единственный конструктивный параметр модели). Система (1)

описывает электрическое и магнитное поля внутри диода и ее решение должно удовлет ворять краевым условиям

Заметим, что краевая задача (1) — (3) является сингулярной, так как условия (2) при их подстановке в (1) приводят к нулевому знаменателю. Поэтому классическое определение решения как удовлетворяющей (2) и (3) пары функций (ф(д), а(х)), обращающих (1) в тождество на отрезке х е [0,1] (с пониманием производных как односторонних на концах отрезка), неприменимо к данной задаче и требуется определить, что понимать под решением (1) —(3).

Мы будем рассматривать систему (1) в об

О — ^(ф, я) : (1 + ф) — я — 1 > о|, на

каждом компактном подмножестве которого правые части (1) имеют ограниченные частные производные и, следовательно, выполнены условия теоремы существования и единственности решения задачи Коши для (1). Кроме того, в силу очевидной симметрии можно ограничиться изучением только решений с положительными 1 + ф (д) и а(д), т. е. вести все рассмотрения в области О₊ = О П {( ф , а) : 1 + ф >  0, а >  0}.

Пусть на правом конце выполняются условия теоремы существования и единственности решения задачи Коши (т. е.

ф (0) — 0, я(0) — 0, ф '

^ = о

0 1 = (1 + ф 1 ) — 1 — Я 1 >0).

Определение. Решением задачи (1) —(3)

ф (1) = ф ,, я(1) = a_v          (3)

будем называть такую определенную на промежутке х е [0,1] и принимающую значения в множестве О₊ дважды дифференцируемую функцию ( ф (х),я(х)) , которая:

• 1)    удовлетворяет краевым условиям на правом конце ( ф (1) = ф ] , а(1) = « 1 );

• 2)    на каждом отрезке х е [ s ,1], 0 < s <  1 обращает исходные уравнения (1) в тождества при подстановке (при этом на концах отрезка производные считаются односторонними);

• 3)    существуют пределы 11m ф ( s ) = 0, s^+ 0

11m a( s ) = 0, 11m ф '( s ) = 0. В точке д = 0 s^+ 0         s^+ 0

эту функцию доопределяем по непрерывности с учетом первых двух равенств из ее третьего свойства.

Особенности данного определения:

• а)    оно не требует подстановки краевых условий с левого конца отрезка в систему, что позволяет уйти от необходимости делить на нуль;

• б)    оно не накладывает никаких ограничений на поведение на левом конце отрезка первой производной а 'Ст) и вторых производных;

• в)    оно может быть очевидным образом модернизировано и на случай 01 = (1 + Ф1)²- 1 - я²= 0, когда сингулярность имеется и на правом конце отрезка.

2. Представление в гамильтоновой форме и интегрируемость. Введем новые обозначения для независимой и зависимых переменных: t = т, qt = ф(х), q2 = а(х), pt =-ф '(х),     р2 = а '(х),

При этом в рамках данного определения допустима и такая ситуация, когда предел производной 11m а '( е ) не существует х ^+ 0

либо является бесконечностью.

Основная цель данной работы — разработать способ построения решения сингулярной краевой задачи (1) —(3) в смысле приведенного выше определения. Для этого мы покажем, что система (1) интегрируется в квадратурах, и построим полную систему первых интегралов. Кроме того, будут получены явные формулы, аппроксимирующие решение краевой задачи вблизи левого конца отрезка.

q = col ( q ^ , q₂ ) е Р² , р = соКр ^ р₂ ) е Р ² и функцию Гамильтона

H ( q , р ⁾ - 2 ( “ Р \ ⁺ Р₂ ) ^{+ j} \С1 + ^q i^{) 2 — q} 2 ^{— 1}-

Тогда систему (1) можно записать в кано

ническом виде:

бН

^q = бр

бН

р - o q

.

Соответственно краевые условия в новых переменных перепишутся так:

q_t(0) = 0, q₂(0) = 0, p_t(0) = 0,     (5)

q i (i) — Q i = Ф 1, ^ ? (1) — Q 2 — ^a i.        ⁽⁶⁾

Новая краевая задача (4) — (6) полностью эквивалентна исходной (1) — (3) и отличается от нее только гамильтоновой формой записи системы дифференциальных уравнений, что позволяет воспользоваться методами интегрирования, разработанными для задач аналитической механики [1].

Гамильтонова система (4) имеет интег

рал энергии

1/2   2\

Л ^{- H (} q , р ^{) —} 2 ( ^- Р 2 ⁺ Р 2 ) ⁺

+ ] (1 + q i ) — q 2 — 1 — C i — const-            (7)

Легко убедиться, что другой первый интеграл системы (4) имеет вид:

/₂ = (1 + q_t)p₂ + q₂p_t = с₂ = const.      (8)

Первые интегралы / 1 и /₂ не зависят явно от времени, являются независимыми (за исключением некоторого двумерного подмножества рассматриваемой области) и находятся в инволюции. Поэтому в соответствии с теоремой Лиувилля [1, § 121, с. 367, § 148, с. 417] модель диода (4) является интегрируемой. Чтобы построить два недостающих первых интеграла, выразим из равенств (7) и (8) импульсы через координаты

ржх12

^р1 “      ₂ +              2

г               г

X (1 + q i ),

X

с ) JС2 - 22 L - ] ^2 -11 с2(1 + 41) \           1)

= x 42-

3. Решение сингулярной краевой задачи. Полагая в (12) t = 1 и используя условия (6) для правого конца отрезка, получаем С 4 = - 1. Аналогичным образом из (11) на

ходим

^с з = 2^ln

где использовано обозначение z ² = (1 + ⁺ 4 i ) ² - ^{4 2}

1 + 0 1 + 0 2

1 + 0 1 - 0 2

. Из условий (2)

или (5) на левом конце отрезка и интегралов (7) и (8) следует, что Р 1 (О) = О, р₂(0) = с₂, с 2> = 2с₁ . Введем в рассмотрение функции

Эти формулы можно представить в ви-

5ф      5Ф де Pi =---, Р2 =---, где функция

5 4 1          5 ^ 2

Ф(41-42- срс2) задается формулой:

Ф(41,42,с1, с2) = ^ In

1 ⁺ 4 1 ⁺ 4 2

^{1 +} 4 1 ^- 4 2

±

V⁽i + ^Q 1 )^{2 - Q} i

P(u,v, Q1, Q2) =      j X zAz

X                                         , m2 (1 - z2 j + 2vz2 Vz2 - 1

(1 + 0 1 )² - о ₂ ²

± ,              -

J ^{(1 +} 4 1 ^{)2 -} 4²

Jс2 - 2 z ²( c ₁ - У Vz² -D

Az .

V (1 + Q 1 )² -Q

G ( u , v ,Q 1 ,Q>) = j x

Интеграл в (11) сводится к элементарным и эллиптическим функциям. В соответствии с теоремой Лиувилля недостающие два первых интеграла выражаются через функцию Ф<41-42-с1-с2):

uA2

2^U² ( 1 - 2 ² j + 2 v2² 2² - 1

5Ф = 1 _ln 1 + 4 1 + 4 2

5 с₂   2    1 + 4 1 - 4 2

(1 + Q 1 )² - Q 2

± j

V ф^)² -^у

C 2 AZ

Z C 2 - 2 z ² (с - yVZ ² - 1 j

Эти функции представимы в виде комбинаций элементарных и эллиптических функций своих аргументов. Из равенств (12) и (13) с учетом полученных из краевых условий соотношений между произвольными постоянными следует, что если с₂ = и* и У = v * являются решением системы двух нелинейных уравнений

F ( u , v , 0 1 ,0 2 ) = 1,

= C g = Const,

т 5Ф _

^ 4 “ Д +

^5c 1

X

J (1 + Q 1 )² -Q2

J X

V ⁽ i ^{+ 4} 1 ^{) 2 - 4} i zAz

1 .

G ( u , v ,0 1 , О 2 ) = 4 In

^{1 + 0} 1 ^{+ 0} 2

^{1 + О} |    ⁰ 2

= t + C 4 ,

то решение краевой задачи (4) —(6) существует и является решением задачи Коши для (4) с начальными условиями на правом конце отрезка, задаваемыми вытекающими из (9) и (10) равенствами: 4 1 (1) = 0 1 ,

c₄ = const.

Полученная полная система четырех первых интегралов (7), (8), (12) и (13) может использоваться в области И , для решения начальных и краевых задач, в том числе задачи (4) —(6).

Р 1 (1) =

u ^ Q ^ Z²

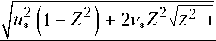
Z2

X

X (1 + Q₁),                  (15)

%<1> = О 2, ^ 2 =

М , (1 + 0 1 ) z ²

дествам (17) и (18). Здесь 8 >  0 — некоторое положительное число. Из (17) имеем

м ,² ( 1 - Z ² ) + 2 v , Z ² 4z ²-1" z ²

,

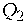
ставляя

- 2с 2 + 2л V2 s + -7= I

У      V2s J это в      (19),

и, под- находим

где Z² = (1 + 0 i ) ² - 0 2

Отметим, что если система (14) несовместна, то это еще не означает, что у краевой задачи (4) —(6) нет решения. Встречаются такие ситуации, в которых в выражениях (9), (10) импульсов через координаты на решении краевой задачи происходит смена знаков и тогда равенства (14) нарушаются.

4. Асимптотика на левом конце.

Будем рассматривать функцию © (х) = (1 + ф (х))² - а(х)² - 1. Продифференцируем эту функцию несколько раз полным образом, используя исходное уравнение (1), тогда получим следующие тождества:

с = 2с₂ - 2 s ² + 4у72 Ё . Важно, что в представлении постоянной с присутствуют только положительные степени малого параметра.

Переходя теперь к пределу при s ^ +0, получаем, что на решении краевой задачи (1) —(3) функция ©(х) удовлетворяет уравнению (19) при с = 2с2 и нулевому начальному условию ©(0) = 0.

Поэтому будем искать приближенное решение (19) в виде © (х) = кх^а , где положительные параметры, т. е. степень а и коэффициент к подлежат определению. Выделяя и приравнивая после подстановки в (19) главные члены в левой и правой частях,

найдем

4 а = —

и

к =

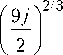
Таким обра

+ 2 у ( © ^{1 / 2} (х) + © ^{1 / 2} (х) ) ,

зом, на левом конце отрезка при малых значениях х >  0 функция © (х) вдоль решения краевой задачи аппроксимируется формулой

Интегрируя дифференциальное уравнение (18), понизим его порядок на единицу: © '' (х) + с = 2у ( 3 ©^{- 1 / 2} ( х ) - © ^{- 1 / 2} (х) ) . (19)

Произвольная постоянная в левой части (19) должна быть взята в соответствии с краевыми условиями (2) и (3). Для этого возьмем произвольное малое положительное число s >  0 и рассмотрим для (1) задачу Коши с условиями ф ( s ) = s , ф '( s ) = s , a (s) = s , a'( s ) = с₂, где, как установлено выше, число С 2 = ^ 2 (0) есть значение постоянной первого интеграла / 2 на решении краевой задачи (1) —(3). Решение этой задачи Коши обозначим через ( ф (х), а (х) ) , а функцию © вдоль этого решения — через © (х). Заметим, что при всех достаточно малых s >  0 начальная точка будет лежать в области О₊, поэтому функция © (х) определена по крайней мере на некотором промежутке [ s , s + 8 ) и удовлетворяет на нем тож

Л2/3

0 (х) = I "1 ]    х ^{4 / 3} .

Подставляя (20) в (1), мы разделяем эту систему на два независимых скалярных уравнения, для которых совершенно аналогичным образом с учетом условий на левом конце отрезка получим приближенные решения

Ф^{( х )} =

1 f 9У У^{2 7 3}

2 I 2 J

' ^4/ 3 ,

а(х) = С 2 Х

f

1 +

У

X f 9/ У ^{2 7 3}

14 У 2 J

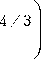
Из (21) и (22) следует, что на плоскости ( ф , а) кривая, дающая решение краевой задачи, аппроксимируется вблизи начала координат следующей функцией:

а = с₂2 ^{3 7 4}

f 9^ Т^ ²

I 2 J

Ф ^3/4

. 1 )

^{1 +} 7 Ф ) '

Задаваемая уравнением (23) кривая выходит изнутри области О , на ее границу в начале координат и имеет в этой точке вертикальную касательную, которая касается и границы области Q₊ . Отметим, что рассматривать задачу Коши для (1) с условиями (2) и а '(0) = С 2 некорректно, так как при этих начальных условиях нарушены условия теоремы существования и подстановка начальных условий в уравнение приводит к делению на нуль. Однако, используя (21) и (22), можно корректно ставить задачу Коши для сколь угодно малого положительного значения независимой переменной д = Д0 = ⁸ >  0.

5. Примеры. Рассмотрим задачу (1) — (3) с единичными условиями на правом конце, т. е. при ^(1) = д2(1) = Q1 = Q2 = 1. Решая соответствующую систему уравнений (14) итерационным методом, найдем ее приближенное решение С2 = и* = 0,8798287042 и j = у* = 0,5337203307. Ему соответствуют вычисленные по формулам (15) и (16) следующие значения импульсов на правом конце отрезка Р1(1) =-1,444231410, Р2^) = = 1,1б2030057. Ниже на рис. 1—7 представлены найденные численным интегрированием справа налево от t = 1 до t = 0 графики компонент решения краевой задачи (толстая линия) и вычисляемые в соответствии с формулами (20) —(23) асимптотики решения вблизи левого конца отрезка (тонкая линия).

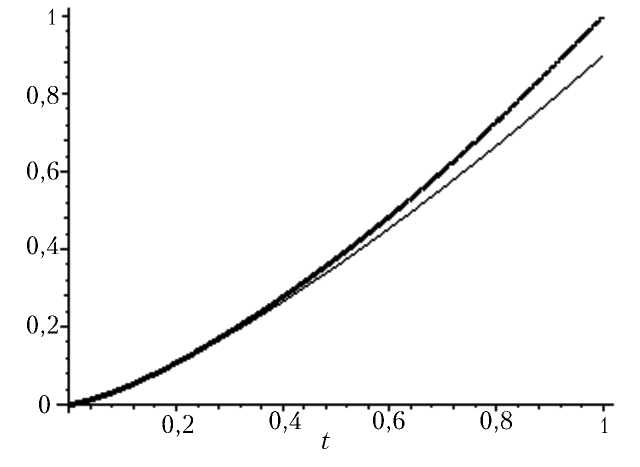
Рис. 1. Решение краевой задачи по первой координате q^ (толстая линия) и его асимптотика по формуле (21) (тонкая линия)

Асимптотика практически совпала с решением, кривые на рис. 2 сливаются.

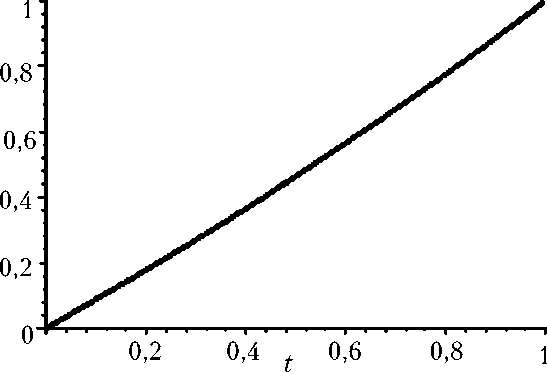
Рис.2. Решение краевой задачи по второй координате q ₂( _t ) (толстая линия) и его асимптотика по формуле (22) (тонкая линия)

Рассмотрим теперь краевую задачу (1) — (3) с существенно различающимися по величине значениями на правом конце, а именно при ^1(1) = Q1 = 10, 72(1) = Q2 = 1- Решая соответствующую систему уравнений (14) итерационным методом, найдем ее приближенное решение: С2 = м* = 0,5404932672 и j = у* = 12,14221503. Ему соответствуют вычисленные по формулам (15) и (16) следующие значения импульсов на пра- вом конце отрезка р1(1) = -16,33935466, ^2(1) = 1,534531629. Приведем только два графика изменения координат для данного варианта исходных данных.

В этом варианте кривые не сливаются полностью, как это было на рис. 2, но, как и на всех других графиках, наглядно проявляется высокая точность представления решения краевой задачи вблизи левого конца отрезка формулами (20) —(23).

0,5

Рис.3. Функция 0 ( t ) вдоль решения краевой задачи (толстая линия) о и ее асимптотика по формуле (20) (тонкая линия)

1,5

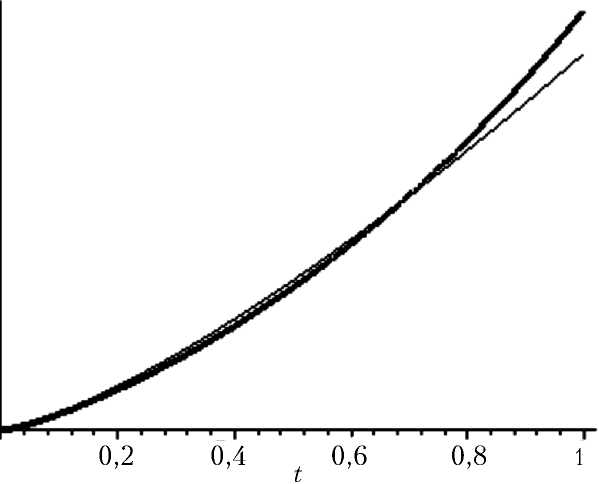
Рис.4. Решение краевой задачи по первому импульсу р₁ (t) (толстая линия) и его асимптотика по формуле (21) (тонкая линия)

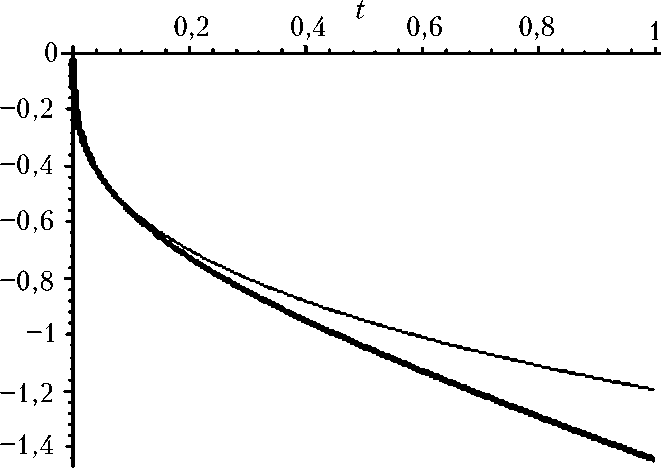
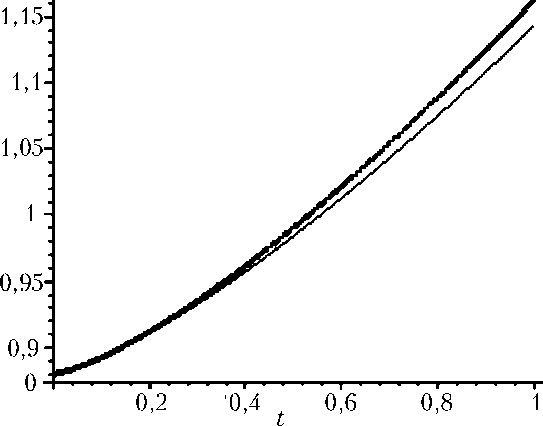
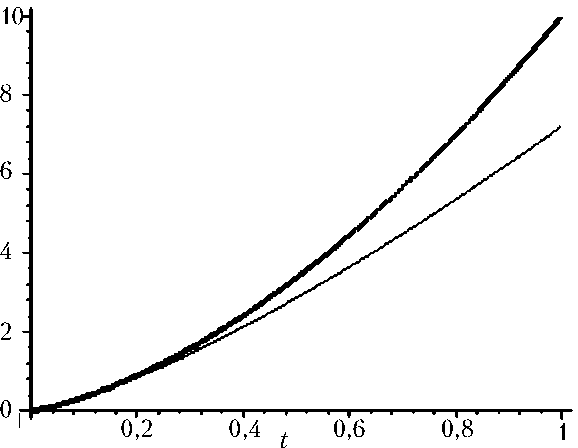
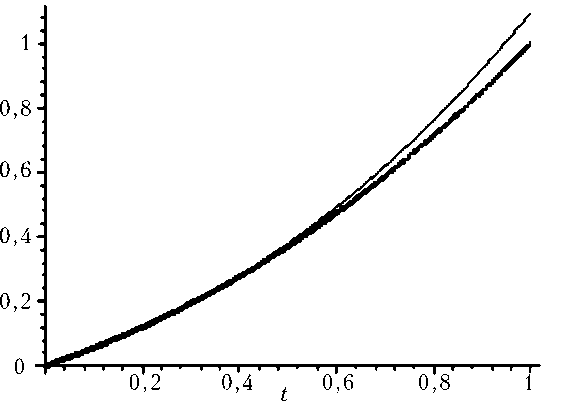
Рис. 5. Решение краевой задачи по второму импульсу Р2^) (толстая линия) и его асимптотика по формуле (22) (тонкая линия)

Рис. 6. Решение краевой задачи по первой координате гр (t) (толстая линия) и его асимптотика по формуле (21) (тонкая линия) для q i (1) = 10, q ₂ (!) = 1

Рис. 7. Решение краевой задачи по второй координате q ₂ ( t ) (толстая линия) и его асимптотика по формуле (22) (тонкая линия) для q i (1) = 10, q 2 (1) = 1