Интегро-дифференциальные уравнения для квазистационарного электромагнитного поля в немагнитном проводящем теле с дефектом

Краевые и начально-краевые задачи электродинамики применительно к проводящим средам имеют существенную прикладную значимость для электротехники, радиотехники и неразрушающего контроля. Уравнения электродинамики в интегро-дифференциальной форме более удобны, чем дифференциальные уравнения Максвелла (как для исследований общего характера, так и для конкретных численных расчетов). Поэтому не теряет актуальность вывод, исследование и решение интегро-дифференциальных уравнений для различных пространственных комбинаций материальных сред (в том числе для задач вихретоковой дефектоскопии).

Ранее были выведены и исследованы интегро-дифференциальные уравнения для неферромагнитного проводника с объемным дефектом [1-3]. Но в этих уравнениях не была использована квазистационарность, типичная для вихретоковых методов неразрушающего контроля. Для ква-зистационарного электромагнитного поля в неферромагнитных проводящих телах тоже были получены интегро-дифференциальные уравнения, но применительно к случаям бездефектных проводников [4, 5]. Однако в контексте вихретоковой дефектоскопии немалый интерес представляет случай неоднородного проводника с объемным дефектом-полостью - в представленной работе получена соответствующая система интегро-дифференциальных уравнений.

Вывод интегро-дифференциальных уравнений

Предположим, что проводящее тело с полостью занимает ограниченную область Q в трехмерном пространстве R³; введем обозначение Q _e = R³ \ Q . Полость занимает область Q 1 , замы-

Марвин С.В. Интегро-дифференциальные уравнения для квазистационарного электромагнитного поля в немагнитном проводящем теле с дефектом кание которой включается в Ω : Ω1 ⊂ Ω . Сторонний ток протекает только в ограниченной области T ; замыкания Ω и T не пересекаются: Ω ∩ T = ∅ . Будем считать, что ∂Ω , ∂Ω1 и ∂T являются поверхностями Ляпунова (символ ∂ для множества обозначает его границу). Кроме того, предположим, что ∂Ω и ∂Ω1 гомеоморфны сфере; из этого, в частности, следует, что Ω и Ω1 объемно и поверхностно односвязны. ∂T гомеоморфна тору; из этого вытекает, что T объемна, но не поверхностно однозвязна (см. рисунок).

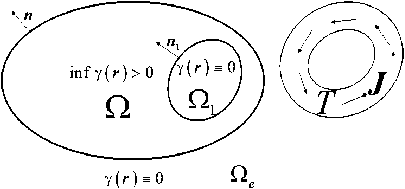
Проводящее тело с объемным дефектом и сторонний ток

Удельная электропроводность γ проводящей подобласти Ω \ Ω ₁ не зависит от времени t . Как функция пространственных координат r = ( x ₁, x ₂, x ₃ ) , γ ( r ) равномерно непрерывна в Ω \ Ω ₁

вместе со своими первыми производными. Кроме того, inf γ ( r ) >  0 . В точках, внешних по от- r ∈ Ω / Ω ₁

ношению к проводящей подобласти Ω \ Ω ₁ , то есть в Ω ₁ ∪ Ω _e , γ ( r ) ≡ 0 и диэлектрическая проницаемость равна 1. Рассматриваются исключительно немагнитные среды, поэтому магнитная проницаемость равна 1 во всем пространстве. Относительно плотности стороннего тока J ( r, t ) будем предполагать, что это непрерывно дифференцируемая векторная функция t ∈ [ 0; +∞ ) и r ∈ T . Кроме того, divJ ≡ 0 и J_{n ∂ T} = 0 , где индекс n обозначает нормальную компоненту.

Заметим, что при отсутствии проводника в области Ω квазистационарное электромагнитное поле определялось бы по известным формулам через объемный векторный потенциал от заданного источника J ( r, t ) ; такое поле называется первичным [5]. Напряженность первичного электрического поля E₀ непрерывно дифференцируема по пространственным координатам при r ∈ ℝ³ . Напряженность первичного магнитного поля H₀ непрерывна при r ∈ ℝ³ , но ее производные терпят разрыв н а ∂ T . Появление проводника в области Ω равносильно появлению вторичных источников в Ω , что не должно сказаться на непрерывности и гладкости итоговых напряженностей в Ω _e . Поэтому при постановке задачи от напряженности электрического поля E и напряженности магнитного поля H при r ∈ Ω _e мы будем требовать наличие тех же свойств непрерывности и дифференцируемости.

Кроме того, E и H должны быть непрерывно дифференцируемыми векторными функциями пространственных координат при r ∈ Ω ₁ и r ∈ Ω \ Ω ₁ , а также должны быть непрерывным образом продолжаемыми на ∂Ω и ∂Ω ₁ с каждой стороны поверхности (хотя при переходе через поверхности раздела сред могут быть разрывы). Кроме того, E и H непрерывно дифференцируемы по времени. То есть речь идет о классическом решении.

В квазистационарном случае, за пределами проводящей подобласти [4]:

f divE = 0

rotE = -^ H

^                                   ,                                              (1)

rotH = J (r, t), r G T rotH = 0, rgQj uQe \T где µ0 – магнитная постоянная; точка над функцией обозначает ее дифференцирование по вре- мени.

В проводящей подобласти (r eQ \ Q1) нет необходимости в уравнении с дивергенцией, по- тому что выводы для divE непосредственно вытекают из уравнений с роторами [4]:

jotE = - ^ ) H rotH = ү ( r ) E

E и H на 3Q и 3Q 1 должны удовлетворять следующим условиям сопряжения [4]:

Xmt = E T e ext

>r,int = Ht,ext ’ где индекс t обозначает касательную компоненту вектора; индексы «int» и « ext» обозначают предельное значение соответственно изнутри и снаружи области.

Также E должна удовлетворять следующему интегральному условию на dQ [4]:

J E n,ext dS = 0,                                          (4)

dQ где dS – элемент площади поверхности.

Кроме того, E и H должны удовлетворять следующим предельным условиям на бесконечности:

E = O (1/r 2), r ^+“

H = O ( 1/r ² ) , r -+» , где r = |r|.

Также в постановке задачи должны фигурировать начальные условия для H : H ( r,0 ) = h ( r ) .

Вектор начальной напряженности электромагнитного поля h ( r ) из физических соображений должен удовлетворять условию соленоидальности: divh ( r ) = 0; тогда из уравнений (1) и (2) вытекает, что при всех t e [ 0; +~ ) divH ( r, t ) = 0 [4].

Решение начально-краевой задачи (1)–(6) – единственное, что доказывается теми же методами, которые были использованы ранее для случая однородного бездефектного проводника [4] (здесь следует обратить внимание на важную роль степеней r в условиях (5)). Кроме того, из (1)–(6) вытекают следующие равенства для H в й³ и E в Q \ Q 1 [6]:

^{H ( r}' t ^{) =}1

Q \Qi

ҮІіЖ dv ■+( J(l4 dv -! 1 Ir — rl T Ir — rl

_w Л     A o f ү ( ^r ' ) ^E ( ^r ' ^e t ' A P ( ^r ' ^e t 1 J f ^E ( ^r ' ^e t ) grad Y ( ^r ' )^

E(r, t ) = —-          —'-VV --- у— dVV +—grad   — _f ? dV -

4n_a\a    r - r          4 n ^J r - r       4 n      < r - r / ( r )

Q\Q1                         T il                Q\Q1    I I' \ /

1 f ^ ( r' ) ,      1 _f c ( r' )    ,

-----grad Ф I----VdS -“---grad Ф -j----/VS ,                       (8) 4n0     dQ lr - rl      4n0     - r - rl где dV – элемент объема; штрих указывает на переменную, по которой производится интегри- рование; E0 - диэлектрическая постоянная; c и c1 - поверхностная плотность вторичных источников, соответственно, на dQ и 3Q1. Заметим, что слагаемые в (7) и (8), содержащие интегралы от J , определяют напряженности первичного поля H0 и E0 соответственно. Также заметим, что в силу (7) H , по существу, является исключенной неизвестной: H выражается через E . А систему уравнений следует решать для E, c и c1.

Уравнения для c и c1 можно вывести, исходя из граничных условий [4], которые, как следствие, вытекают из (1)-(3): nEint = 0 и n1E ext = 0, где n и n1 - внешние единичные нормали со- ответственно для ∂Ω и ∂Ω1 (см. рисунок). В силу формул для предельных значений нормальной производной потенциала простого слоя [6]:

µ 0 ε 0 γ ( r ′ ) n ( r ) E ( r ′ , t ) dV _′+ µ 0 ε 0 n ( r ) J ( r ′ , t ) dV _′+ ε 0

2π Ω∫      r-r′             2π T∫ r-r′         2πΩ\∫Ω1

E ( r ′ , t ) grad γ ( r ′ )

r - r′ 3 γ( r′)

(r -r′)n(r)dV′-

-

1 f г^р (r - r‘) n (r)dS'- 1~ § r1(ri3 (r - r‘) n (r)dS'+a(r )=0, r edQ;

^{2 π} ∂Ω r - r ′                    ^{2 π} ∂Ω ₁ r - r ′

µ 0 ε 0 γ ( r ′ ) n 1 ( r ) E ( r ′ , t ) dV _′+ µ 0 ε 0 n 1 ( r ) J ( r ′ , t ) dV _′+ ε 0       E ( r ′ , t ) grad γ ( r ′ ) ₍ r _- r _{′ )} n_{1 (} r ₎ dV _′-

2π Ω∫       r-r′              2π T∫    r-r′          2πΩ\∫Ω1 r-r′3γ(r′)

-

1Г f r ( rl ( ^r - ^r ‘ ) n¹ ( ^r ) ^dS'- f r 1^ri 3 ( ^r - ^r ‘ ) n¹ ( ^r ) ^dS '- г ( ^r ) = 0 , ^{r edQp      (10)}

^{2 π} ∂Ω r - r ′                    ^{2 π} ∂Ω ₁ r - r ′

В знаках (9) и (10) учтено, что для ∂Ω речь идет о пределе изнутри, а для ∂Ω ₁ – снаружи. В отличие от ранее полученных уравнений для немагнитных бездефектных проводников [4, 5], в (8)–(10) совокупно учтены неоднородность и дефектность (присутствуют соответствующие объемные и поверхностные вторичные источники), и одновременно с этим исключена H , что, очевидно, упрощает решение. Непосредственным дифференцированием, с использованием свойств объемных и поверхностных потенциалов, доказывается, что решение (7)–(10) удовлетворяет не только уравнениям (2) при r ∈ Ω \ Ω ₁ , но также уравнениям (1) при r ∉ Ω \ Ω ₁ и граничным условиям (3).

Условие (4) для nE _ext равносильно следующему:

∫ σ dS = 0 .                                      (11)

∂Ω

У σ и σ1 есть конкретный физический смысл: это поверхностные плотности зарядов, индуцируемых на ∂Ω и ∂Ω1 соответственно (делитель 4πε0 в (8) делает это соответствие не пропорциональным, а буквальным). Таким образом, условие (4) – это условие электронейтральности внешней поверхности проводника ∂Ω (заметим, что для Ω \ Ω1 и для ∂Ω1 электронейтральность следует из самих уравнений и граничных условий, так что ее не нужно отдельно требовать). Уравнения (8) и (9) сами по себе содержат неоднозначность, связанную с σ [7]: к σ можно прибавить любое равновесное распределение зарядов на ∂Ω – условие (11) эту неоднозначность устраняет.

Из (2) и (6) следуют начальные условия для E в Ω \ Ω ₁ :

E(r,0) =

1 γ(r)

roth ( r )

Уравнения (8)–(10) удобны тем, что их достаточно решить для Ω \ Ω ₁ , ∂Ω и ∂Ω ₁ при условиях (11) и (12): тогда E в Ω ₁ и Ω _e определяется из (8) прямым интегрированием (можно найти E , например, на каком-либо измерительном контуре в Ω _e ). Так как ∂Ω и ∂Ω ₁ являются поверхностями Ляпунова, на (8)–(10) распространяются все основные теоремы, касающиеся интегральных уравнений со слабой особенностью [7]. H можно найти прямым интегрированием в (7).

Заметим, что выражение (8) для E содержит не только производные от объемных потенциалов и потенциалов простого слоя, но и непродифференцированные объемные потенциалы (первая пара слагаемых в правой части). В общем случае при r → +∞ для объемного потенциала гарантирована асимптотика O ( 1 r ) , но не O (1 r ²) . Покажем, что тем не менее условие (5) для (8) выполняется (в ранее рассмотренных случаях бездефектных проводников [4, 5] этому внимание не уделялось).

По условию J как функция пространственных координат имеет нулевую дивергенцию в T и нулевую нормальную составляющую на границе T ; очевидно, такими же свойствами обладает

J. үЕ и үЕ обладают аналогичными свойствами в Q \ Q1. Для неодносвязных областей с глад- кими границами, гомеоморфными сфере или тору, доказано, что любое такое поле представимо в виде rot w, где divw = 0 и на границе области wT = 0 [8]. Преобразуем интеграл из второго сла- гаемого в правой части (8) (для первого слагаемого преобразования выполняются аналогично):

f j(r', t)     . rrot'w(r', t)          c f       dV' = J r dV = J rotr’

T l^r-rl T     l^r-rl              T

^ w ( r ¹ , t )

v r r' >

dV '- J grad r ’

T _

( 1 л           1

I    x ^w ( r^, t ) ^dV =

V l^{r - r}I J            J

Г [ n T ( ^r )^{x w} T ( r^Z, t ) J d r         l^{r - r}1

dS' + J grad r t _

( 1 л

I-----Л ^xw ( ^r , t )

V lr - r J

dV' = J rot r T

^ w ( r', t ) л

v ‘ >

w r,t dV' = rot [ . ( ,,) dv', T lr-rl

где индекс у дифференциальной операции указывает на переменную, по которой происходит дифференцирование; n _T – внешняя единичная нормаль к T . Таким образом, рассматриваемый интеграл может быть представлен, как ротор от объемного потенциала, и тогда асимптотика O (1 r ²) гарантирована.

Заключение

Несомненную актуальность представляет обобщение полученных результатов, во-первых, на ферромагнитные проводники и, во-вторых, на проводящие тела с негладкими границами (с возможным переопределением функциональных классов, в которых ставится задача, с отказом от классического решения и переходом к решению обобщенному). Это станет предметом дальнейших исследований.