Интеллектуальная поддержка принятия решений при управлении ресурсами сложных систем на основе многоагентного подхода

Управление ресурсами сложной системы необходимо для обеспечения её эффективного функционирования. В условиях динамично изменяющихся внешних условий к модели сложной системы предъявляются требования адаптивности и возможности быстрого реагирования на изменения. При этом к системе поддержки принятия решений (СППР) необходимо предъявлять следующие требования:

• ■    при построении плана решения задачи необходимо учитывать индивидуальные свойства, присущие однородным ресурсам, которые используются для решения задач, поскольку это существенно влияет на эффективность принимаемых решений;

• ■    система должна быть готова к разным непредвиденным ситуациям, нарушающим построенный план, и при необходимости должна оперативно находить и предлагать лицу, принимающему решения, возможные варианты альтернативных решений, устраняющих эти последствия, с предварительной оценкой.

Задачи управления ресурсами как одного из разделов исследования операций исследованы в работах Р. Акоффа [1], Л. Берталанфи [2], С. Бира [3], Р. Беллмана [4] и др. [5, 6]. Проблемам оптимизации ресурсов в многоуровневых территориально-производственных системах посвящены работы А.Г. Гранберга [7].

Особый интерес представляют работы учёных самарской школы. Фундаментальные проблемы принятия решений в условиях агентного взаимодействия и распределения ресурсов на базе сетей потребностей и возможностей рассмотрены в цикле работ, выполненных под ру- ководством В.А. Виттиха (см., например [8]). Разработке интеллектуальных систем управления ресурсами с использованием мультиагентных технологий и сетецентрического подхода посвящены работы П.О. Скобелева [9].

Вопросы разработки моделей многоагентной самоорганизации при управлении сложными системами исследуются в работах В.И. Городецкого [10].

Анализ основных исследований [11] в области управления распределением ресурсов в сложных системах показал, что большинство разработанных методов работают только с числовыми данными и не учитывают слабо формализуемую информацию об особенностях предметной области (ПрО), а также индивидуальные особенности, присущие ресурсам одного вида.

В связи с этим данная статья посвящена разработке моделей и методов поддержки принятия решений при управлении сложными системами в условиях неопределённости и ресурсных ограничений. Первый раздел посвящён постановке задачи управления ресурсами с использованием семантических ограничений ПрО. Во втором разделе представлен обобщенный алгоритм распределения ресурсов. В третьем разделе определены принципы и требования разработки СППР при управлении ресурсами в сложных системах с использованием многоагентного подхода. В четвертом разделе приведён пример практического использования разработанных моделей и алгоритмов для решения задачи управления ресурсами в чрезвычайных ситуациях (ЧС). Пятый раздел посвящен описанию разработанного прототипа и оценке эффективности на примере задачи управления ресурсами в чрезвычайных ситуациях.

1    Постановка задачи управления ресурсамис использованием семантических ограничений предметной области

Задачи управления ресурсами могут иметь разные формулировки, суть которых сводится к тому, что требуется оптимальным образом распределить имеющиеся ресурсы для достижения определённых целей. Под оптимальностью в данном случае может пониматься качество распределения ресурсов. Критерием оптимальности может быть максимум прибыли, минимум затрат и т.п. Имеются определённые ограничения на сами ресурсы и их использование при достижении целей.

Для обобщения таких задач логично использовать единую терминологию. При формулировке задачи управления ресурсами будем использовать следующие понятия:

• ■    ресурсы - это всё то, что используется для решения каких-либо задач;

• ■    потребители ресурсов - это любые сущности, которые используют ресурсы для достижения своих целей и решения задач.

Рассмотрим формальную постановку классической задачи управления ресурсами 1 .

Дано:

N - количество видов ресурсов;

M - количество потребителей ресурсов;

R = { r 1 , „., r n } - множество ресурсов, n = 1,.., N ;

U = { u i , „., u m } - множество потребителей ресурсов, m = 1,.., M ;

Введём множество пар р={ r i /u j }, элементы которого p j = r i /u j характеризуют распределение (выделение, назначение) ресурса r i для потребителя u j .

Введём критерий f (ρ), позволяющий оценить качество распределения. Требуется найти такое распределение ресурсов, чтобы значение этого критерия было бы максимальным:

f p) ^ max.

¹ Далее авторы отождествляют управление ресурсами с распределением ресурсов. Ред .

Имеются три вида основных наиболее распространённых ограничений, которые могут быть представлены следующим образом:

• ■    O ( R ) - ограничения по ресурсам;

• ■    O ( U) - ограничения по потребителям ресурсов;

• ■    O ( R xU) - ограничения, связанные с конкретным распределением ресурсов.

Таким образом, классическая задача распределения ресурсами может быть сформулиро-

вана в следующем виде:
	f ( р ) ^ max
	при ограничениях
(1)	о ( R ),
	о (и ),
	о ( R X и ).

В то же время на практике очень часто возникают задачи, связанные с распределением ресурсов, которые не укладываются в классическую постановку. Это происходит из-за того, что при формулировке задачи распределения ресурсов приходится учитывать ряд ограничений, не представленных в (1). В основном это сложно формализуемые семантические ограничения нечисловой природы. При попытке формализации таких ограничений и сведении такой задачи к классической постановке вида (1) получается достаточно громоздкая и трудно воспринимаемая модель. При этом , чем более сложные ограничения рассматриваются, тем более трудоёмок процесс сведения задачи к классической.

Для иллюстрации таких ограничений рассмотрим пример задачи доставки заказов покупателям, когда необходимо распределить имеющиеся в наличии транспортные средства (ресурсы) для доставки заказов (потребители ресурсов) покупателям. Помимо стандартных ограничений на вместимость грузов и т.п. вводится ограничение на несовместимость определённых видов заказов, например, продукты питания и бытовая химия не могут перевозиться одновременно на одном автомобиле.

Эти ограничения гораздо сложнее, рассмотренных нами ранее. Формально записать такое семантическое ограничение для двух потребителей можно в виде O ( RxUxU ). Классический пример такого рода ограничений представлен в задаче о перевозке волка, козы и капусты на лодке с одного берега на другой. Однако, ограничение может связывать несколько потребителей ресурсов и тогда в общем виде оно запишется как O ( R xUxUx_xU) .

Другой вид ограничений присутствует в задачах, когда потребителю ресурсов для достижения своей цели требуется не один, а несколько ресурсов. При этом ограничения обычно накладываются на порядок или технологию использования этих ресурсов. Для простого случая с двумя ресурсами ограничения представимы в виде O ( RxRxU) .

В общем случае ограничение, накладываемое на использование нескольких видов ресурсов для конкретного потребителя ресурсов, запишется в виде O ( RxRx ... xRxU) .

В качестве примера задачи с такими ограничениями можно привести задачу с прохождением пациентами (потребители ресурсов) отдельных процедур (ресурсы) в медицинском учреждении [12]. При этом ограничения на несовместимость двух и более процедур или порядок прохождения этих процедур для конкретного пациента (например, по медицинским показаниям) как раз укладываются в такую схему.

Более сложные ограничения, охватывающие несколько ресурсов и несколько потребителей ресурсов, описываются ограничениями вида O ( RxRx_xRxUxUx_xU) .

Таким образом, существуют постановки задач распределения ресурсов с использованием семантических ограничений, которые не всегда возможно свести к задаче (1) или же такое сведение нецелесообразно ввиду усложнения модели задачи. Поэтому в общем виде задача распределения ресурсов с использованием семантических ограничений запишется в виде:

'f(p) ^ max при ограничениях :

■ O ⁽ R X о (U ), _ O ( R X ... R X U X ... X U ).

2    Обобщённый алгоритм распределения ресурсов

Предлагается использовать для решения задач управления ресурсами многоагентные технологии. При этом в качестве базовой используется модель агентов, предложенная Вулд-риджом и Дженнингсом [13]. Агентам многоагентной системы для решения задач распределения ресурсов соответствуют, во-первых, сущности, выступающие в реальном мире потребителями и/или поставщиками ресурсов, а во-вторых, сами ресурсы. Для решения задачи распределения ресурсов агенты вынуждены взаимодействовать и вступать друг с другом в переговоры, которые моделируются коммуникациями.

В большинстве случаев задача распределения ресурсов имеет глобальный критерий эффективности, который необходимо достичь путём соответствующего распределения ресурсов. Тогда поведение агентов можно считать кооперативным, поскольку только учёт взаимных интересов позволяет решить задачу. В то же время каждый агент может иметь свои локальные критерии, определяющие эффективность полученного решения для конкретного агента. Например, одно решение может быть более предпочтительным по сравнению с другим на основе использования локальных критериев эффективности, несмотря на то, что они могут быть абсолютно одинаковы с точки зрения общего критерия эффективности.

Многоагентные технологии позволяют успешно решать задачи управления ресурсами с учётом как глобальных, так и локальных критериев.

Общая схема решения задачи распределения ресурсов может быть представлена в виде обобщенного алгоритма, представленного на рисунке 1.

Любые сложно формализуемые семантические ограничения ПрО представляются в виде онтологической базы знаний, доступной агентам. Кроме этого, база знаний агента используется для описания критериев, отражающих приемлемость распределения ресурсов, и учитывает индивидуальные особенности моделируемых объектов реального мира.

При ведении переговоров агенты определяют допустимость и приемлемость для них решения на основе индивидуальной базы знаний. Таким образом, если меняются критерии и предпочтения у какого-то агента, достаточно внести изменения в его локальную базу знаний. При этом сама процедура ведения переговоров остается без изменений.

3    Основные принципы разработки системы поддержки принятия решений при управлении ресурсами

С учётом предъявляемых требований предлагается использовать следующие основные принципы системного подхода [14], заложенные в основу разрабатываемой СППР.

• ■    Принцип конечной цели . В процессе формулировки задачи управления ресурсами постулируется цель, которая является общей для всех агентов, функционирующих в рамках многоагентной системы. Приоритет глобальной цели над локальными целями агентов оз-

• начает, что, несмотря на наличие у каждого агента собственной локальной цели, достижение глобальной цели является более приоритетным.

• ■    Принцип измерения. Глобальная и локальные цели формализуются в виде некоторых математических оценочных функций, поддающихся вычислению. Это необходимо для того, чтобы агенты демонстрировали целенаправленное поведение, то есть любые действия, принимаемые агентами, должны оцениваться с помощью введённых оценочных функций.

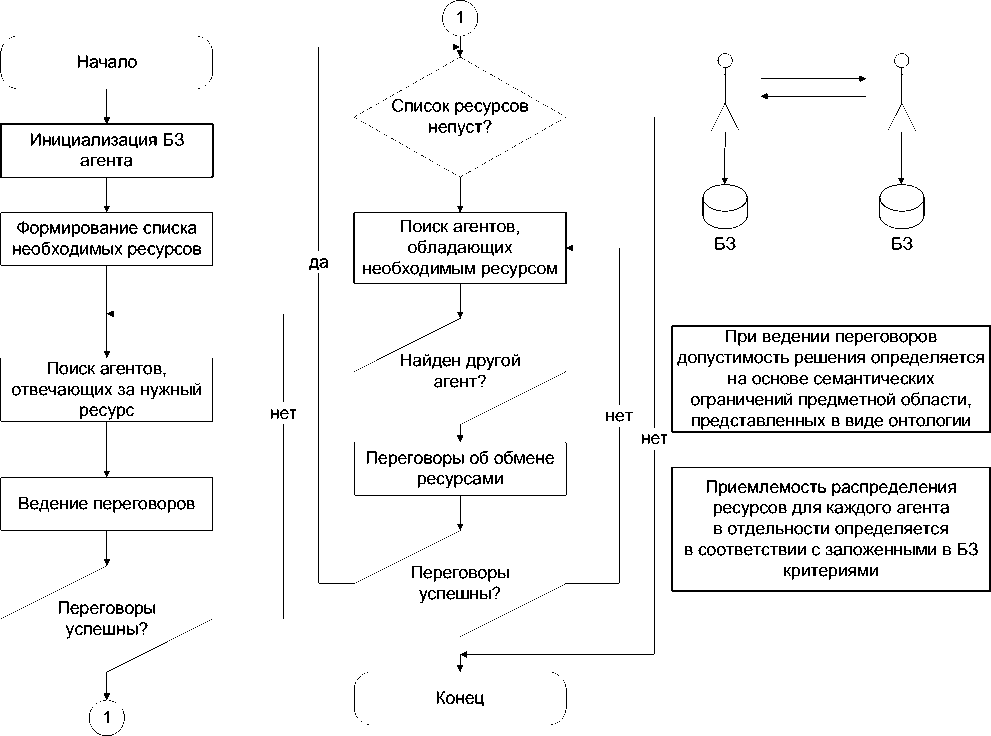
Рисунок 1 - Блок-схема обобщённого алгоритма (слева) и семантические ограничения ПрО (справа) распределения ресурсов с использованием многоагентных технологий

• ■    Принцип эквифинальности . Желаемое или целевое состояние системы в виде некоторого допустимого и приемлемого плана распределения ресурсов может быть получено практически из любых начальных условий, из которых в принципе существует возможность получения допустимых решений. При этом траекторий достижения целевого состояния мо жет быть неско лько, и они мо гут о тличаться, в том числе, и планами р аспределения ресурсов.

• ■    Принцип единства . СППР при управлении распределением ресурсов в сложных системах базируется на многоагентной системе, которая представляет собой совокупность взаимодействующих агентов. Каждый из них является либо потребителем, либо поставщиком ресурсов. При этом, несмотря на то, что агенты представляют собой автономные сущности, семантический и прагматический смысл их проявляется только тогда, когда они существует в виде некой единой многоагентной системы.

• ■    Принцип модульного построения . Система рассматривается как совокупность взаимодействующих агентов (модулей) многоагентной системы.

• ■    Принцип развития . Принципы, заложенные в СППР, базирующуюся на применении многоагентных технологий, позволяют системе развиваться и адаптироваться, учитывая при этом любые возможные изменения внешней среды и самой системы.

• ■    Принцип децентрализации . При построении СППР при управлении ресурсами в сложных системах с использованием многоагентного подхода закладываются принципы самоорганизации, что означает отсутствие какого бы то ни было центра управления, решающего, что, кому и как делать. Решение каждый агент принимает самостоятельно в соответствии с заложенными в него критериями и правилами поведения.

• ■    Принцип неопределённости . Применение многоагентных технологий и модели окружающей внешней среды позволяет учитывать фактор неопределённости, когда внешние воздействия не всегда полностью определены.

В структуре СППР можно выделить следующие виды обеспечений: математическое, алгоритмическое, информационное, методическое и программное. Рассмотрим содержание каждого из них при проектировании СППР при управлении ресурсами в сложных системах в условиях динамично изменяющейся внешней среды и семантических ограничений.

В состав математического обеспечения разрабатываемой СППР необходимо включить математические модели агентов, участвующих в решении задачи распределения ресурсов. Кроме этого должны быть сформулированы основные цели и критерии, позволяющие оценить эффективность распределения ресурсов.

Алгоритмическое обеспечение должно включать набор алгоритмов, обеспечивающих решение основной задачи распределения ресурсов, а также вспомогательных задач – рационального размещения агентов по узлам вычислительной сети и восстановления работоспособности агентов в случае сбоя.

При разработке информационного обеспечения необходимо предусмотреть возможность хранения слабоструктурированной информации в базе данных и сложно формализуемых знаний в базе знаний СППР. Если СППР разрабатывается для предприятия, то она должна интегрироваться с существующими информационными системами для получения доступа к имеющейся актуальной информации.

В состав методического обеспечения должны входить методики, позволяющие подготовить и сформировать весь набор необходимых исходных данных для решения задачи управления ресурсами.

Программное обеспечение должно обеспечивать решение задач поддержки принятия решений по управлению ресурсами в режиме реального времени. Кроме этого, должна быть предусмотрена возможность отслеживания реализации разработанного и принятого плана распределения ресурсов и, в случае необходимости, оперативного внесения корректировок в случае непредвиденных обстоятельств или сбоев.

Рассмотрим далее применение предлагаемого алгоритма и принципов разработки СППР для решения задачи управления ресурсами в условиях ЧС.

4 Пример применения многоагентных технологий при управлении ресурсами в условиях чрезвычайных ситуаций

ЧС характеризуются высокой степенью неопределённости и динамичностью. Это означает, что мы обладаем лишь частичной информацией о ситуации в определённый момент времени и практически ничего не можем сказать о будущем ситуации. Мы не можем, например, точно сказать, сколько пострадавших, какой характер их поражений. Доступные ресур- сы также меняются динамически, например, спасатели и транспорт могут прибывать в течение всего периода ликвидации последствий ЧС. Также в условиях ЧС важно быстро и рационально распределить имеющиеся в наличии ограниченные ресурсы с целью минимизировать возможные потери, связанные, в первую очередь, с человеческими жизнями. Кроме того, необходимо соизмерять затраты с решаемыми задачами (например, чтобы доставить пострадавшего, жизни которого ничто не угрожает, достаточно использовать автомобиль, а не вертолёт). Все подобные факторы делают задачу управления ресурсами очень сложной.

Задача решается в рамках проекта SpeedUp [15, 16], целью которого является разработка средств, обеспечивающих информационную поддержку для взаимодействия и коммуникации специальных спасательных служб в ЧС.

Рассмотрим задачу рационального распределения ресурсов в условиях ЧС на примере транспортировки пострадавших в больницы. Во время ЧС представляет интерес следующая информация о пострадавшем:

• ■    общие сведения о пострадавшем (ФИО, пол, возраст);

• ■    характер и степень повреждений;

• ■    местоположение пострадавшего;

• ■    вид транспорта, необходимый для эвакуации пострадавшего в больницу.

В зависимости от тяжести полученных повреждений, возраста пострадавший должен быть доставлен в ту или иную больницу (обычную или специализированную, например, ожоговую). Для его транспортировки также требуется выбрать транспортное средство (например, автомобиль или вертолёт). При этом больницы имеют ограниченное число свободных мест для приёма пострадавших.

Проект SpeedUp строится на базе сервис-ориентированной архитектуры, которая хорошо подходит для управления и распределения ресурсов в целом, а также на использовании семантических услуг, что позволяет осуществлять динамическое распределение ресурсов во время выполнения.

На основе проведённого анализа возможных представлений ресурсов в виде сервисов [16] была предложена схема, по которой каждый вид ресурса (транспорт, больницы) описывается с помощью одного сервиса с соответствующей функциональностью. Однако имеющиеся недостатки такого представления, связанные со спецификой ПрО [16], не позволяют должным образом решать задачу рационального распределения ресурсов. Применение классических алгоритмов рационального распределения ресурсов в условиях динамично меняющейся внешней среды представляется весьма затруднительным, поскольку мы имеем дело с неполной и нечёткой информацией.

В многоагентном подходе каждый ресурс представляется с помощью агента. В данном случае можно выделить три основных класса агентов: пациенты, транспорт и больницы.

• ■    Больницы - это статичный класс агентов, который обладает информацией о своём местоположении, количестве свободных мест в данный момент, а также специфических характеристиках больницы (взрослая/детская, ожоговый центр и т.д.).

• ■    Пациенты - это активный класс агентов, в который заложена информация о местоположении, поле, возрасте, диагнозе, степени тяжести и т.д. Эти агенты обладают целью -«доставить себя» до больницы, соответствующей их диагнозу и степени тяжести, в установленное время (которое тоже может задаваться в характеристиках агента).

• ■    Транспорт - класс агентов, обладающий следующими характеристиками: вид, текущее местоположение, место постоянной дислокации (куда нужно вернуться после доставки пациента), скорость, специфические особенности транспорта (связанные с диагнозом и тяжестью).

В соответствии с анализом представления ресурсов, проведённым в [16], общую схему решения можно представить в виде, показанном на рисунке 2.

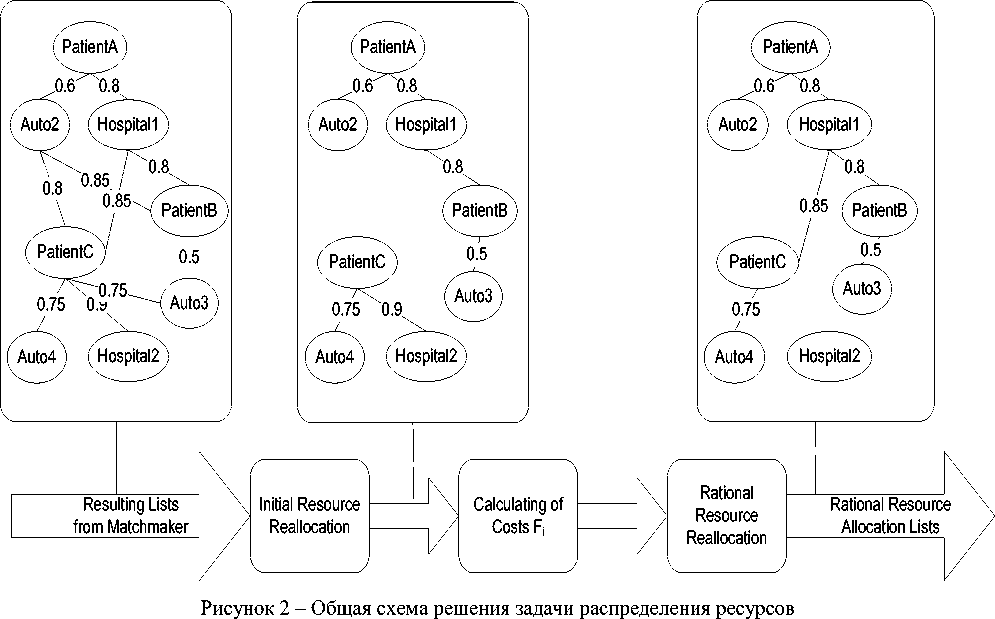
На входе имеются списки пациентов и выделенных им ресурсов, упорядоченных по степени соответствия параметрам запроса.

Каждый пациент имеет список ресурсов, которые могут быть ему выделены для транспортировки. Каждый элемент такого списка имеет числовую характеристику, отражающую предпочтительность (степень соответствия) выделенных ресурсов потребностям пациента (которые были заданы в параметрах запроса). Соответствующие списки с числовыми характеристиками получаются в результате обработки запросов (рисунок 3).

На первом этапе решается задача первоначального распределения ресурсов с учётом их ограниченности. Например, может оказаться, что в качестве лучших решений для нескольких пациентов будет выдан транспорт Auto1 , в то время как по условиям задачи транспортное средство используется для перевозки только одного пациента. Аналогичная ситуация и с больницами, которые имеют ограниченное количество свободных мест (в данном случае ситуация сложнее). Задача решается путем взаимных уступок, при этом в качестве критерия может быть выбран минимум потерь пациентом в соответствующей характеристике предпочтительности (степени соответствия) выбранных ресурсов.

То есть в данном случае при уступке ресурса пациент А теряет (0.8 - 0.7) = 0.1, а пациент В (0.9 - 0.7) = 0.2. Следовательно, уступить должен пациент А . В то же время, если для пациента А 2-е значение для транспорта было бы, допустим 0.4, а не 0.7, то тогда уступить должен был бы пациент А .

Рассмотрена ситуация для двух пациентов, аналогично осуществляется распределение ресурсов для большего числа пациентов.

	0.8	0.7	0.5	0.1
PatientA	Auto1	Auto2	Auto8	Auto6
	Hospital	Hospital	Hospital	Hospital
	1	4	3	2
	0.9	0.8	0.8	0.4
	0.9	0.7	0.6	0.3
PatientB	Auto1	Auto3	Auto2	Auto4
	Hospital	Hospital	Hospital	Hospital
	2	4	3	1
	0.8	0.7	0.6	0.2

Рисунок 3 - Фрагмент упорядоченных списков выделенных ресурсов

Таким образом, происходит первоначальное распределение ресурсов на основе информации, полученной в результате обработки запросов.

На следующем этапе производится попытка улучшить полученное решение путём обме- на между пациентами ресурсами, имеющимися в списках.

Для описания поведения агентов при распределении ресурсов в ЧС разработана математическая модель, включающая критерии их рационального поведения [16]. В нашем случае у агентов, которые решают задачу, есть цель, которая достигается рациональным поведением. Введём следующие обозначения:

P ={ P 1 ,..., P N } - множество пациентов;

A ={ A 1 ,..., A M } - множество транспортных средств;

H = { H 1 ,.., H R } - множество больниц;

I - индекс пациента;

• j - индекс транспортного средства;

• к - индекс больницы;

Ху_к - факт доставки пациента i на транспортном средстве j в больницу к ( X_i j _k = 1, если пациент i перевозится на транспортном средстве j в больницу к, или X ijk = 0, если иначе);

Z ( P i , A j ) - затраты на перевозку пациента P i в транспортном средстве A j ;

D ( P i , H_k ) - расстояние от местоположения пациента P i до больницы H_k ;

Free ( H k ) - количество свободных мест в больнице H k ;

S ij - коэффициент, отражающий предпочтительность транспортного средства j для транспортировки пациента i ;

S_ik - коэффициент, отражающий предпочтительность транспортировки пациента i в больницу к : 0 <  S ij < 1, 0 <  S_ik < 1. Чем ближе S ij (или S_ik ) к 1, тем более предпочтительны выделенные ресурсы, и наоборот.

Требуется найти такое распределение ресурсов (матрицу X ijk ), при котором целевая функция, отражающая затраты на транспортировку пострадавших в больницы с учётом степени соответствия выбранных для этой цели ресурсов, была бы минимальна:

F = £ £ £ X j [ Z ( P , A j ) D ( P , H k )]

i = 1 j = 1 к = 1

s j * 5 ,к

> min.

При этом должны быть учтены следующие ограничения:

• 1)    Одно транспортное средство может использоваться для транспортировки только одного пациента:

NR

ЕЕ X jk = 1. ^v j ■ i =1 k =1

• 2)    Для транспортировки одного пострадавшего используется только одно транспортное средство:

MR

ЕЕ X» = 1.v 1 ■ j =1 k=1

• 3)    Количество пострадавших, транспортируемых в конкретную больницу, не должно превышать количества свободных мест в ней:

NR

ЕЕX,k ^ Free(Hk).vk ■ i=1 k =1

• 4)    Для транспортировки пострадавших используется только такой вид транспорта, который соответствует характеру и тяжести повреждений (семантическое ограничение задачи).

• 5)    Пострадавший может быть доставлен только в определённый тип больницы в соответствии с характером и тяжестью повреждений (семантическое ограничение задачи).

• 6)    Время транспортировки пострадавшего в больницу (если оно является критическим для пациента и определено) не должно превышать установленной величины.

Представленная математическая модель, подробно описанная в [16], позволяет найти рациональное распределение ресурсов для транспортировки потерпевших в больницу. Но иногда на практике бывают ситуации, когда транспортировка пострадавшего в наиболее подходящую для него больницу не является хорошим решением. Это может быть связано с тем, что в это же время некоторые пострадавшие транспортируются в ту же больницу. Тогда эта больница будет испытывать трудности с приёмом и обслуживанием пострадавших из-за ограниченности собственных ресурсов (операционных, врачей и т.д.). В то же время есть другие больницы, которые не перегружены приёмом пострадавших. В этой ситуации лучшим решением было бы транспортировать пострадавшего в одну из таких больниц.

Рассмотрим пример. Пусть имеется 6 больниц и 10 пострадавших. И предположим, что только 2 больницы являются наиболее подходящими для 10 пострадавших. Тогда 10 человек должны перевозиться только в эти две больницы. В этом случае эти больницы будут испытывать трудности с приёмом пострадавших, поскольку они не могут иметь достаточного количества операционных и медицинского персонала для обслуживания пострадавших в один момент времени. В то же время остальные 4 больницы не задействованы. Это решение не является эффективным. Хорошим решением будет распределить пострадавших в больницы равномерно, чтобы не перегружать медицинский персонал.

Отличительной особенностью данной модификации постановки задачи является то, что рациональное поведение агентов должно учитывать равномерное (без перегрузок обслуживающего персонала) распределение пострадавших в больницы. Это означает, что пострадавшие, поступающие в больницу, не должны создавать заторов при приёме.

Введенное нами ограничение может быть представлено функцией, учитывающей возможности приёма потока пострадавших больницами. Таким образом, целевая функция с учётом введённых условий примет следующий вид:

F = _{Е ЕЕ} X jk [ Z ( P i , A j ) D ( P , H k )]

* № ( N M X jk ) ^ ^min . k = 1        i = 1 j = 1

j k

г = 1 j = 1 k = 1

R   NM где: П Uk (^^ Хук ) - множитель, учитывающий условие равномерности поступления по-к=1       i=1 j=1

страдавших в больницы с учётом их возможностей;

NM

^^ X_ijk - общее количество пострадавших, транспортируемых в больницу к;

i = 1 j = 1

U_k ( q ) > 1 — величина, отражающая увеличение расходов, связанных с приёмом большего количества пострадавших, чем больница может принять в обычных условиях.

В качестве базовой принята модель рефлексивных агентов, предложенная Вулдриджом и Дженнингсом [13].

Каждый агент-пациент имеет цель, которая представлена в виде функции полезности. Особенность решаемой задачи определяет характер взаимодействия и поведения агентов-пациентов при достижении поставленных целей. В нашем случае поведение агентов-пациентов не является антагонистическим, так как они должны работать вместе, чтобы решить общую задачу - все они должны быть доставлены в больницы при помощи соответствующих транспортных средств при минимальных затратах. С учётом указанных обстоятельств функция полезности, которая определяет поведение агентов-пациентов, не принимает во внимание их собственную выгоду, а учитывает в целом затраты на транспортировку всех пострадавших. С другой стороны, агент-пациент имеет информацию о стоимости только своей транспортировки (эта величина может быть рассчитана). Для достижения своих целей агенты-пациенты ведут переговоры друг с другом. Суть этих переговоров состоит в том, чтобы при совместном использовании ресурсов (транспортных средств, больниц) для достижения собственных целей получить лучшее решение. Таким образом, общая целевая функция и, следовательно, функция полезности для каждого агента-пациента улучшится.

Рассмотрим более подробно, как происходит процесс переговоров.

Пусть каждый агент-пациент умеет вычислять (и хранит вычисленное значение) функцию затрат на собственную транспортировку F i :

Fi =

z ( Pi , Aj) d ( Pi , H )

S *S, ij ik

.

Далее предположим, что у нас есть пациенты A и B , которые имеют соответствующие стоимости затрат на их транспортировку F A и F B соответственно. Допустим, в процессе коммуникации два агента-пациента решили обменяться какими-либо ресурсами (транспортными средствами или больницами), при этом подразумевается, что в результате обмена семантические ограничения задачи будут соблюдены. После обмена эти два агента-пациента будут иметь новые стоимости затрат на их транспортировку - F'_A и F' B соответственно. При этом, если новые суммарные затраты на транспортировку окажутся меньше предыдущих затрат, то есть F A + F' B < F A + F B , то целесообразно провести такой обмен ресурсами, поскольку общие затраты на транспортировку пострадавших снизятся.

На базе агентной платформы JADE2 разработан прототип многоагентной системы, в которой реализованы три типа агентов (пациенты, больницы и транспорт) [16]. Фрагмент исходной информации о пострадавших и выделенных им ресурсах приведён ниже.

Этот XML-код хранит информацию о пациентах, транспортных средствах и больницах, необходимую для функционирования многоагентной системы. Для каждого агента-пациента присутствует информация о степени соответствия выделяемых ему ресурсов.

В результате работы прототипа создаётся схожий по структуре xml-файл, содержащий информацию о пациентах и выделенных им ресурсах.

5 Прототип системы поддержки принятия решений для распределения ресурсов в чрезвычайных ситуациях

На рисунке 4 представлен интерфейс разработанного прототипа СППР для распределения ресурсов в ЧС.

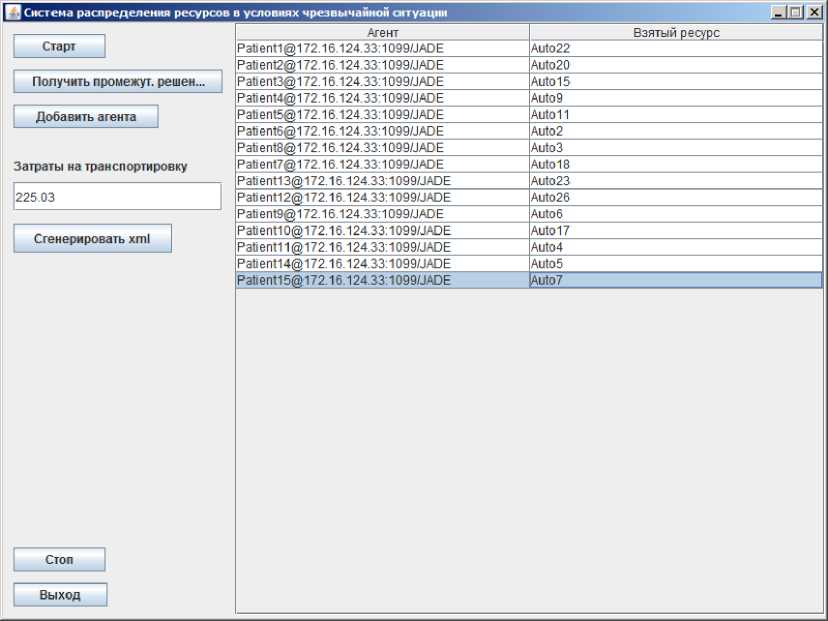
Рисунок 4 – Интерфейс разработанного прототипа СППР

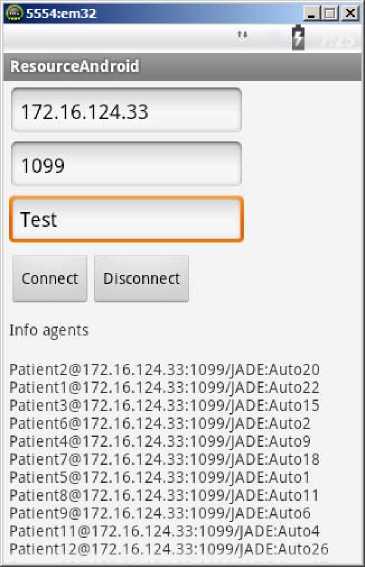
Рисунок 5 - Интерфейс мобильного приложения СППР

Интерфейс создан с целью демонстрации возможности программы. Чтобы приступить к работе, достаточно нажать кнопку «Старт». После этого произойдет загрузка данных и генерация агентов. Система запустится, и начнется распределение ресурсов между агентами. Результаты распределения можно наблюдать в режиме реального времени в правой части графического интерфейса прототипа.

Для увеличения мобильности приложения разработана клиентская версия для мобильной платформы, управляемой операционной системой Android. Мобильное приложение даёт следующие преимущества:

• ■    предоставление актуальной информации о пострадавших, а также информации о транспорте, который для них необходим;

• ■    организация обмена информацией между основным управляющим центром и всеми клиентами, что в свою очередь позволяет поддерживать актуальность данных.

Интерфейс разработанной версии приложения для мобильных платформ представлен на рисунке 5. При подключении к серверу на нём создается новый агент, отвечающий за связь устройства с многоагентной системой. После этого появляется возможность свободно обмениваться сообщениями с другими агентами. Далее созданный агент отправляет запрос на получение данных и в качестве ответа получает информацию о текущем состоянии агентов и выводит данные на форму. Актуальность информации поддерживается путём периодических запросов на её получение.

Для оценки эффективности алгоритма перераспределения ресурсов была проведена серия экспериментов. Полученные решения сравнивались с исходными значениями затрат, полученными в результате работы программы, используемой для решения этой задачи, подробное описание которой можно найти в [17].

Были проведены эксперименты с различным количеством пострадавших и ресурсов.

Первоначальная информация была сгенерирована на основе данных о количестве пациентов и имеющихся ресурсах. Информация о степени соответствия назначенного ресурса генерировалась случайным образом. В результате были созданы наборы тестовых данных.

Анализ результатов показал, что суммарные затраты на транспортировку пострадавших уменьшаются в среднем на 15-55% по сравнению с первоначальным распределением.

Заключение

Предложена модель задачи управления ресурсами сложных систем с учётом семантических ограничений ПрО, которая положена в основу разработки математического обеспечения СППР. Определены принципы разработки и структура СППР. Результаты апробации разработанных моделей позволяют судить о работоспособности и эффективности предлагаемых алгоритмов в плане повышения оперативности управления ресурсами за счёт возможности учёта индивидуальных особенностей моделируемых сущностей реального мира и слабо формализуемых семантических ограничений ПрО.

Исследование частично поддержано грантами РФФИ 14-07-00811-а, 15-07-01565-а.