Интеллектуальное робастное управление динамически неустойчивым объектом. Ч 1: удаленная настройка баз знаний на технологии мягких вычислений

Рассмотренные ранее решения задачи стабилизации [2, 3], представляли собой на нижнем уровне управления классический ПИД-регулятор, используемый в 80% производственных и автоматизированных системах. Макет системы, используемый в физическом эксперименте, имел датчик угла отклонения и ПИД регулятор в качестве регулятора на нижнем уровне. Развитием решения данной задачи является настройка системы управления с несколькими контурами обратной связи и соответствующими ПИД регуляторами. Применительно к макету, таким расширением является добавление дополнительной обратной связи в контур управления в виде сигналов с энкодеров двигателей. Такая обратная связь позволяет установить положения макета относительно горизонтальной оси. Примеры решение такого рода задачи рассматриваются в [4].

Проектирование интеллектуальной системы управления (ИСУ) обычно используется для платформы нечетких систем на основе мягких вычислений. Существенным недостатком таких систем является отсутствие стандартной методики конструирования баз знаний (БЗ) нечетких систем управления.

Одной из основных проблем эффективного применения технологии мягких вычислений в задачах управления являлось решение следующих задач:

объективное определение вида функции принадлежности (ФП)  и ее параметров  в продукционных правилах в БЗ;

определение оптимальной структуры нечетких нейронных сетей (ННС) в задачах обучения (аппроксимация обучающего сигнала с требуемой (заданной) ошибкой и с минимальным количеством продукционных правил в БЗ – определение универсального аппроксиматора);

применение генетического алгоритма (ГА) в задачах многокритериального управления при наличии дискретных ограничений на параметры объекта управления (ОУ) с целью согласования причинно-следственных связей в продукционных правилах.

Перечисленные проблемы были решены и апробированы на основе Оптимизатора Баз Знаний (ОБЗ) с применением технологии мягких вычислений. Разработанный интеллектуальный инструментарий позволил проектировать робастные БЗ на основе решения одной из алгоритмически трудно решаемых задач теории искусственного интеллекта – извлечения, обработки и формирования объективных знаний без использования экспертных оценок. В данном оптимизаторе используются три ГА, которые позволяют спроектировать оптимальную структуру нечеткого регулятора (вид и число ФП, их параметры, а также число самих правил нечеткого вывода), аппроксимирующей обучающий сигнал с требуемой ошибкой.

При этом автоматически проектируется оптимальная структура нечеткой нейронной сети и формируется модель универсального аппроксиматора в виде нечеткого регулятора с конечным числом продукционных правил в БЗ.

В данной работе рассматривается возможность использовать удаленное соединение с ОУ для настройки БЗ нечеткого регулятора (НР) на основе ОБЗ с применением технологии мягких вычислений. Такая возможность позволяет проектировать ИСУ без использования системы стохастического моделирования, что дает преимущество при проектировании нечетких систем управления для сложных и плохо формализованных ОУ.

Дистанционная настройка БЗ дает возможность максимально адаптировать нечеткую систему управления для конкретной (непредвиденной) ситуации управления не зависимо от времени и места нахождения ОУ. Такого рода самоорганизующиеся ИСУ с дистанционным проектированием БЗ важны, например, для ликвидации последствий аварий на АЭС, при разборе завалов при землетрясениях, крушении поездов, для работы в загрязненной и радиоактивной окружающей среде и т.д.

Структура и основные функции ОБЗ

Применительно к проектированию ИСУ, мягкие вычисления представляют собой комбинацию из следующих подходов: теория нечетких системы, генетические алгоритмы (ГА) и нечеткие нейронные сети (ННС).

НР является центральным элементом ИСУ и вырабатывает управляющие сигналы изменения во времени (законы управления) коэффициентами усиления k , k , k ПИД-регулятора. Ядро НР основано на процессе проектирования БЗ, которая интегрирована в интеллектуальный контроллер. Структурно БЗ состоит из продукционных логических правил, которые включают нечеткие входные и выходные значения функции принадлежности лингвистических переменных.

Функциональная структура ИСУ с блоками НР и ОБЗ на мягких вычислениях представлена на рис. 1.

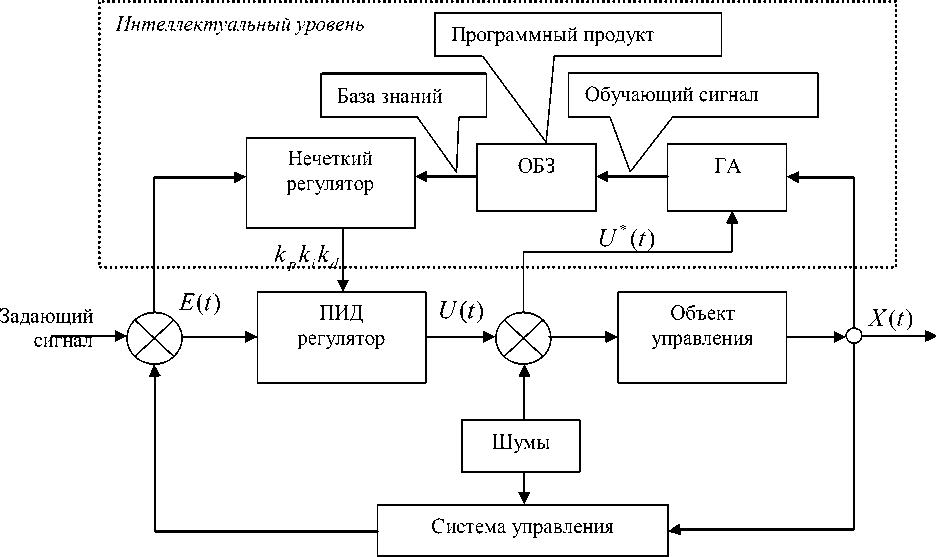
Рис. 1. Структура ИСУ с нечетким регулятором и оптимизатором баз знаний

Такая структура включает одновременно следующие качества управления: управляемость, точность и устойчивость (нижний уровень управления – САУ) и обучение и адаптация (верхний интеллектуальный уровень управления – НР с БЗ).

Наиболее актуальной проблемой при создании ИСУ является получение оптимальной и робастной БЗ, которая гарантирует достижение требуемого уровня качества управления. При

Электронный журнал «Системный анализ в науке и образовании» Выпуск №4, 2013 год проектировании БЗ возникают трудности, связанные со сложностью динамической системы и наличием шумов в системе измерения и управления.

Входом ОБЗ является обучающий сигнал (ОС), который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из результатов измерений динамических параметров физической модели ОУ. ОС является источником знаний и представляет собой массив данных, разделенный на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В общем виде, каждый из составляющих сигналов является выборочной (репрезентативной) траекторией некоторого случайного процесса. При этом подразумевается, что в каждый момент времени существует некоторая корреляция между входными и выходными сигналами. Например, в случае аппроксимации некоторого управляющего сигнала, входными компонентами могут являться ошибка управления, интеграл ошибки и ее производная, а выходным компонентом -требуемое значение управляющего воздействия, либо некоторые настраиваемые параметры системы управления, например коэффициенты усиления ПИД-регулятора.

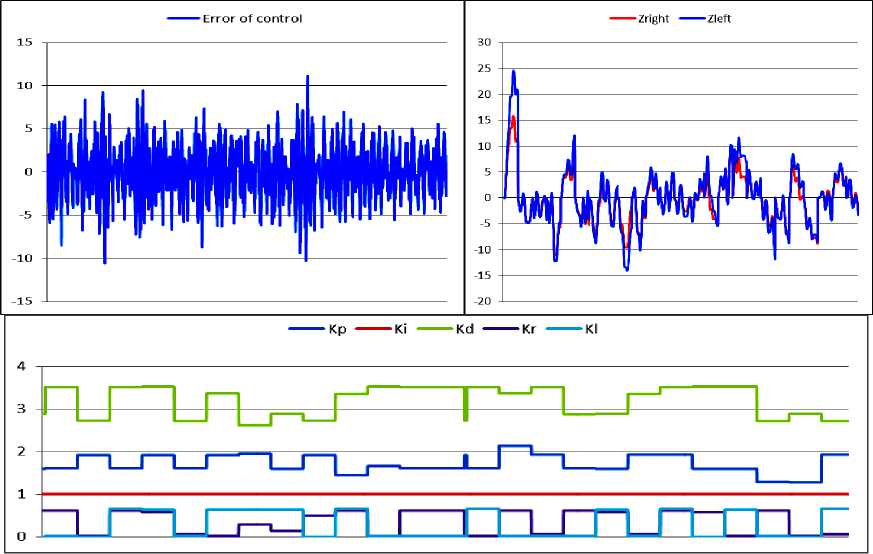
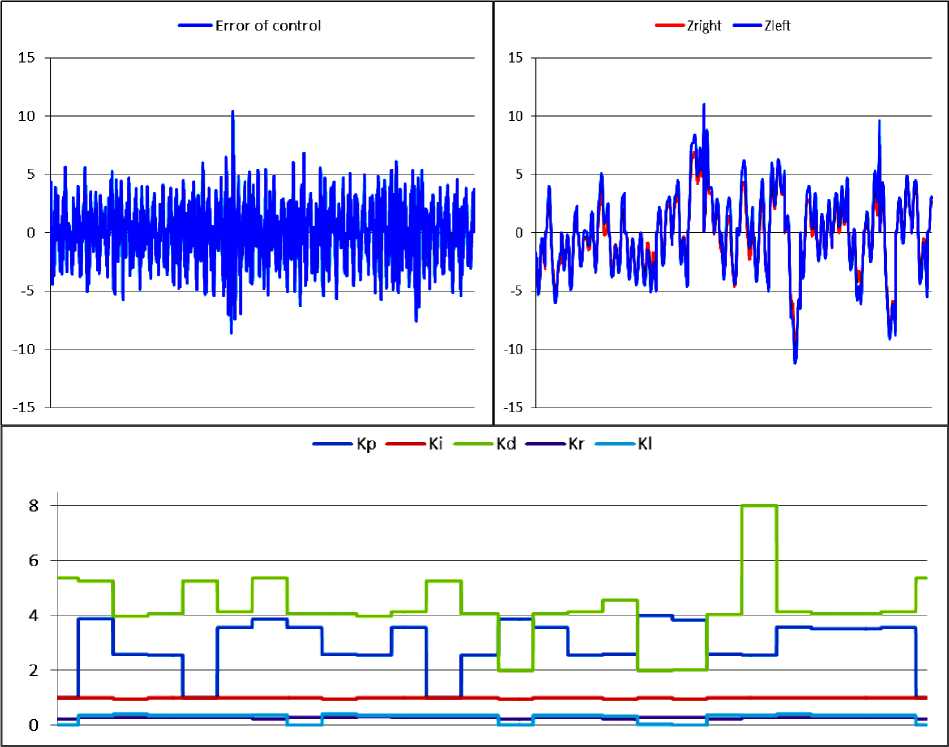
На рис. 2, входными данными для НР является вектор ошибки, который состоит из ошибки управления e ( t ), интеграла ошибки управления ie = eedt и скорости изменения ошибки управления ^{e (} t ).

		1 ^i/f 0			kd-
-0. 01	-0. 01	-0. 01	13. 38	0.48	20.13
-0. 02	-0. 01	-0. 04	13. 38	0.48	20. 13
-0. 04	-0. 01	-0. 07	13. 38	0.48	20.13
-0. 05	-0. 01	-0.12	13. 38	0.48	20.13

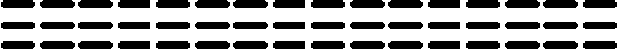
0.2 5    -0.02   7.67    14.20   0.30    16.26

0.18    -0.07   7.84    14.20   0.30    16.26

Рис. 2. Обучающий сигнал

Выходными данными НР является вектор, состоящий из значений коэффициентов усиления к , k_d , k_t ПИД-регулятора, значения которых применяются в формировании управляющего воздействия в виде:

u ( t ) = k_p ( t ) e ( t ) + k ( t ) je (r) d-c + k_d ( t ) e ( t ).                            (1)

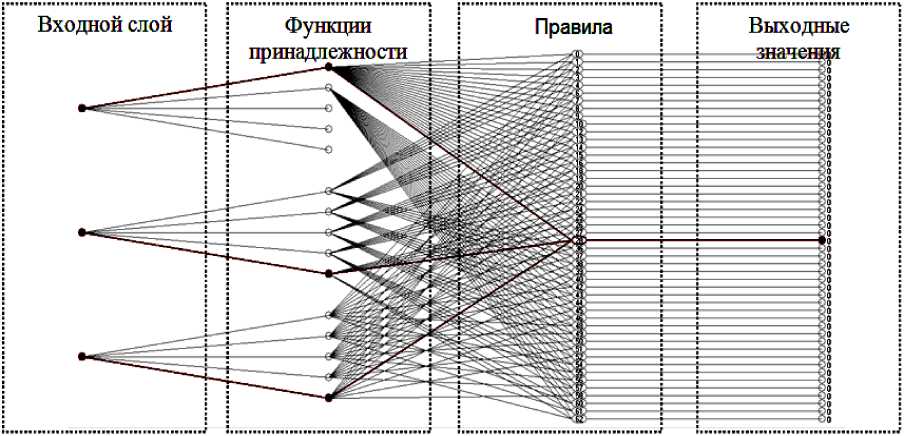
Структурно ОБЗ состоит из взаимосвязанных генетических алгоритмов (ГА1, ГА2, ГА3), оптимизирующих отдельные компоненты БЗ [1]. Базовые шаги оптимизации и структура ОБЗ представлены на рис. 3.

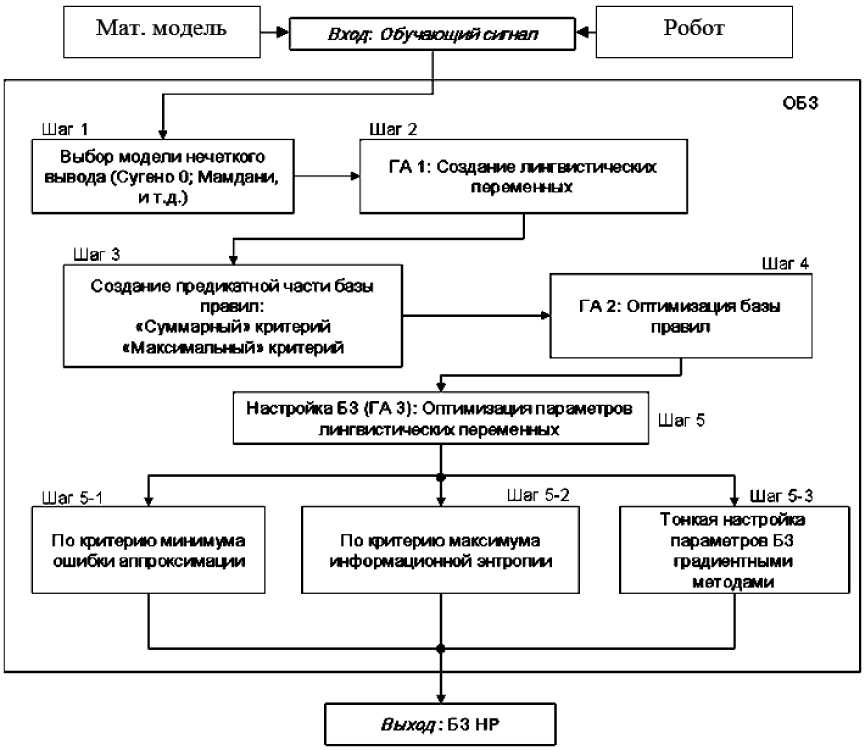
Рис. 3. Структура ОБЗ и шаги оптимизации

Рассмотрим шаги алгоритма оптимизации [1]:

Шаг 1 : Выбор модели нечёткого вывода . Пользователь определяет тип нечёткой модели вывода (Сугено, Мамдани, и т.д.), и число входных и выходных переменных.

Шаг 2 : Создание лингвистических переменных . С помощью ГА1 определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее функций принадлежности (треугольная, Гауссовская и т.д.).

Шаг 3 : Создание базы правил . На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии со следующими двумя критериями:

«суммарный» критерий: выбрать только те правила, которые удовлетворяют следующему условию:

R total _ fr ^ TL ,                                                 (2)

где TL (threshold level) – заданный (вручную или выбранный автоматически) уровень активации правила, и

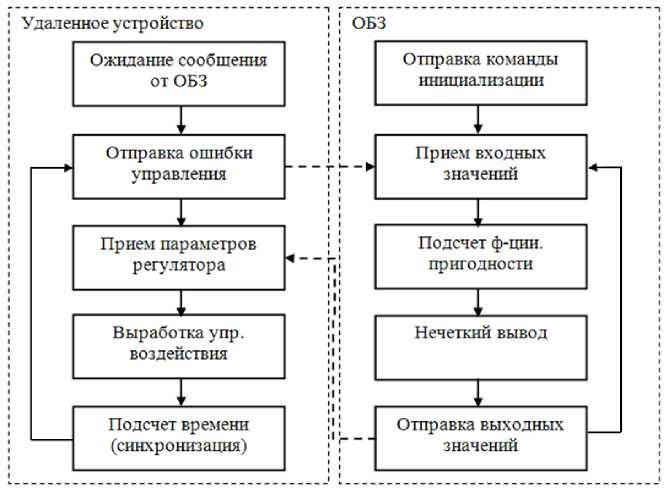
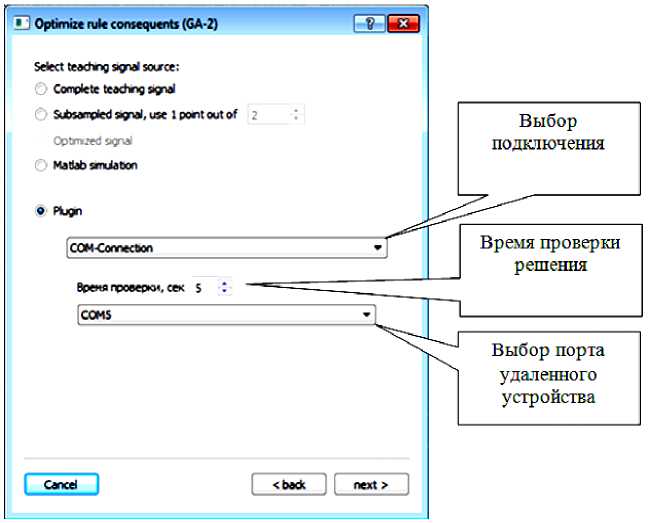
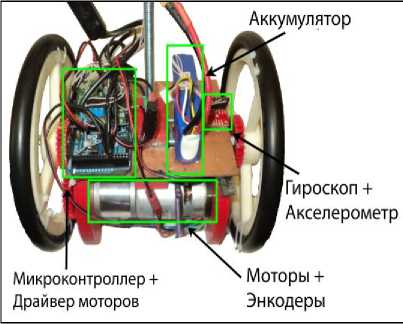
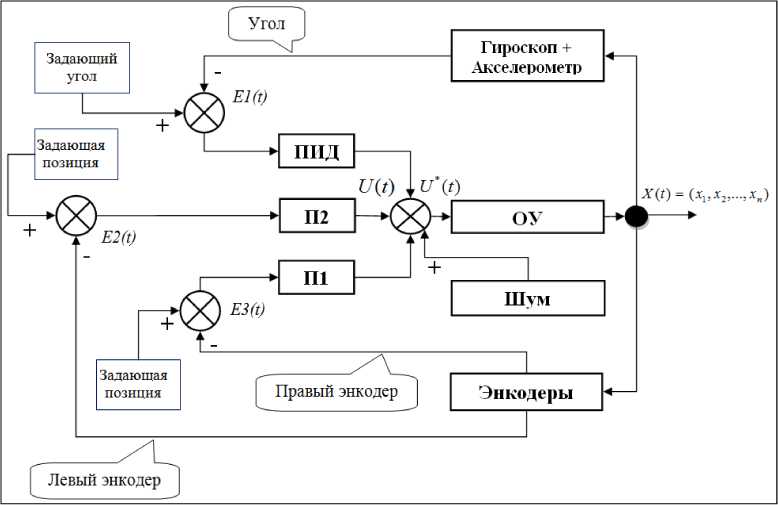
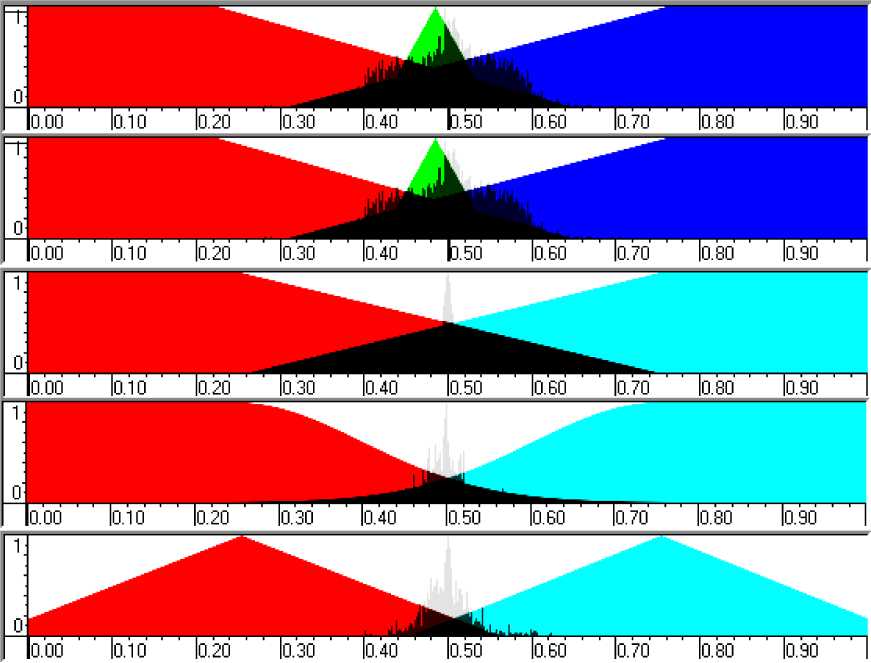
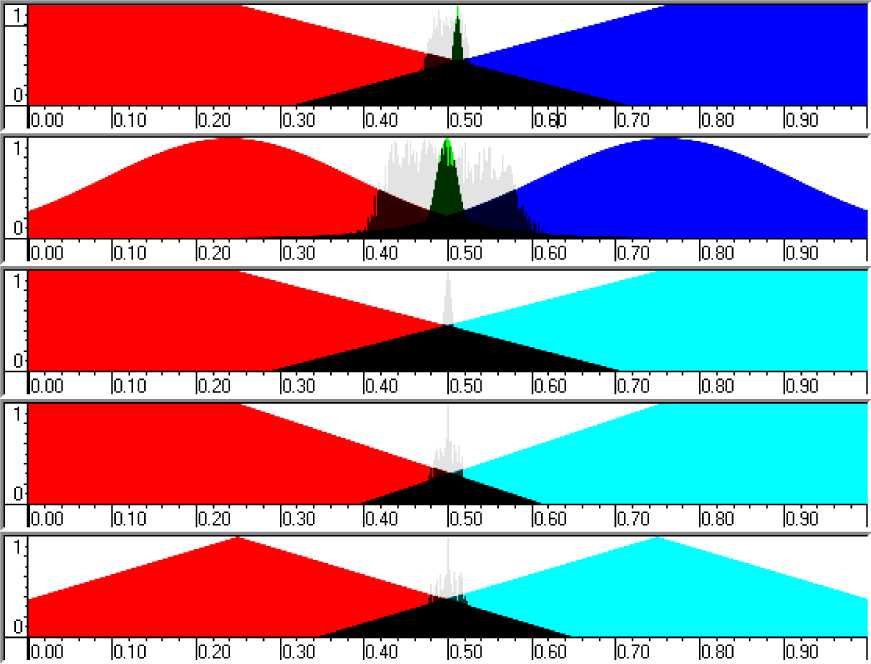
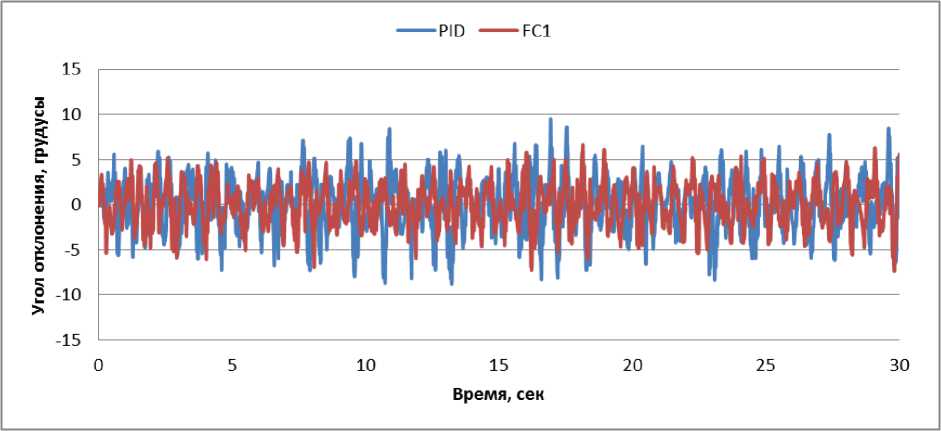
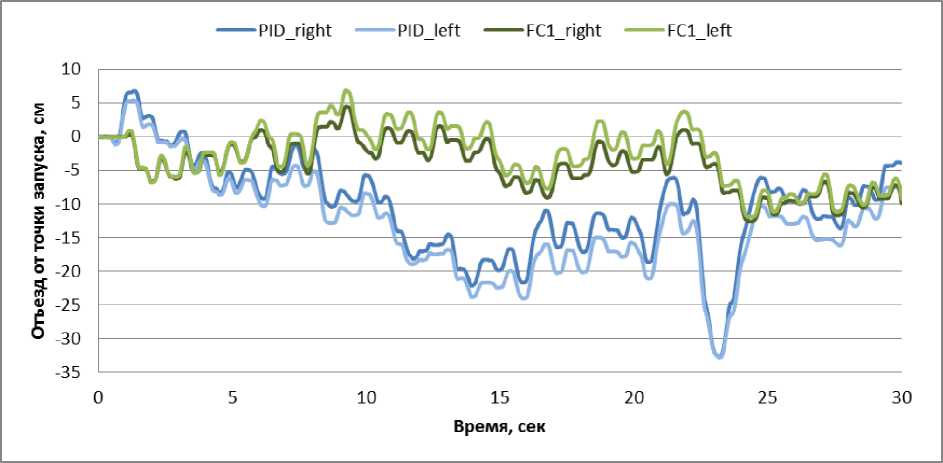
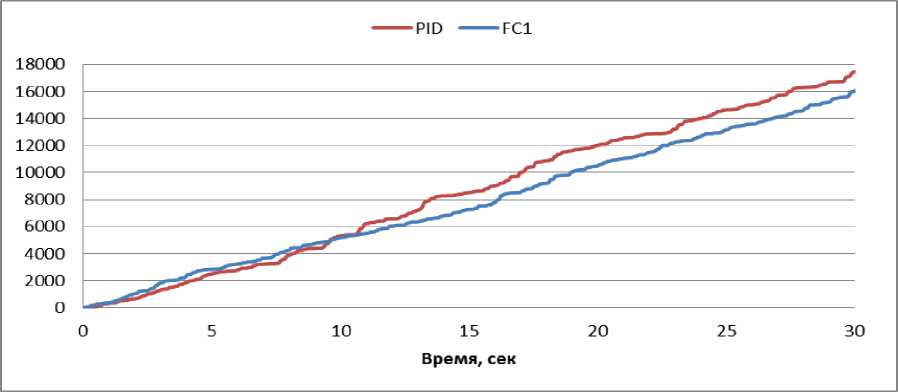
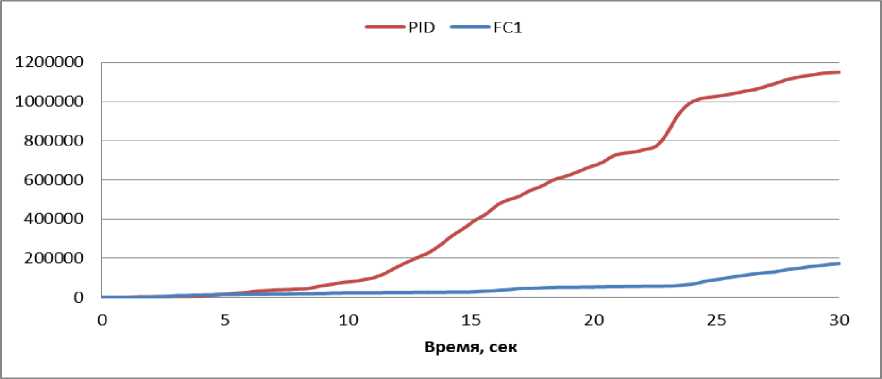
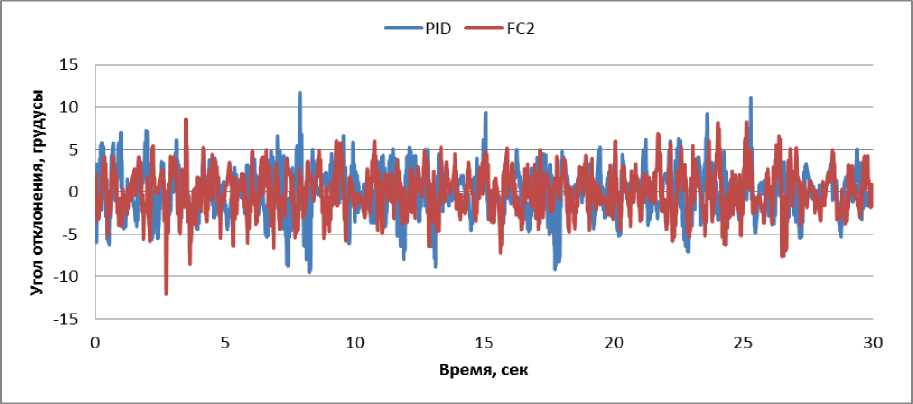
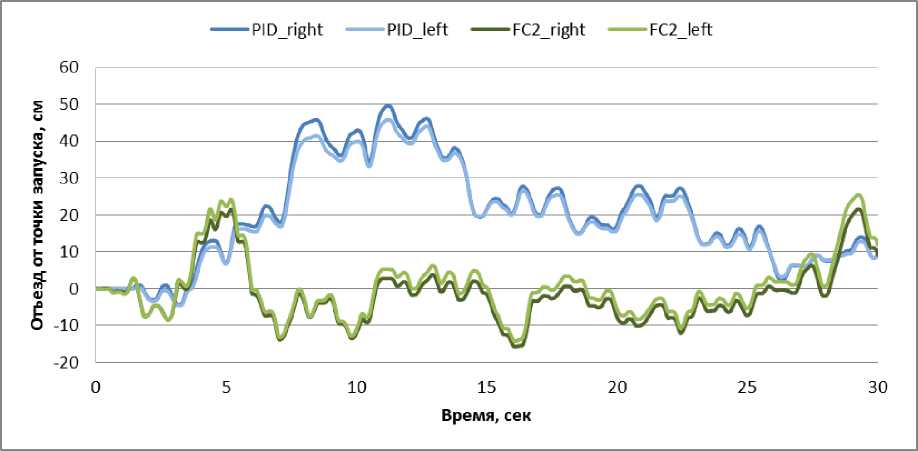
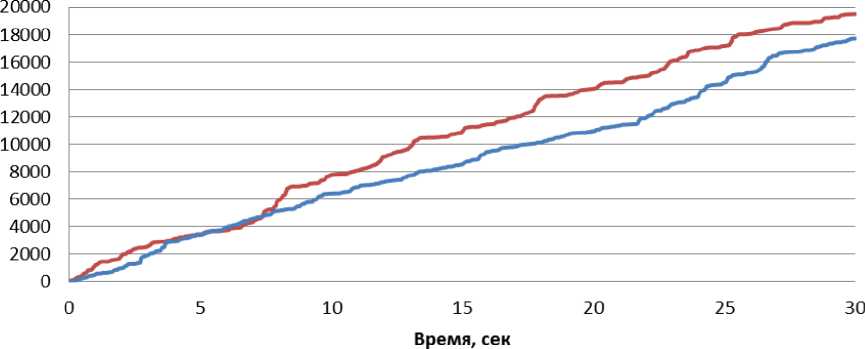
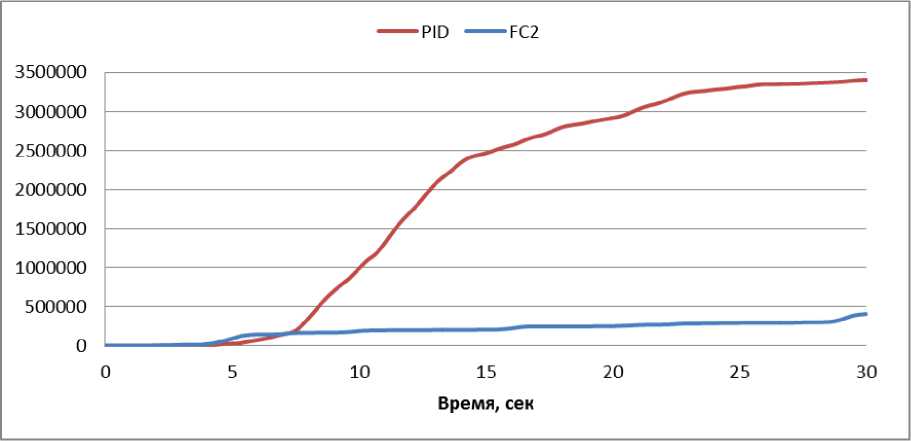
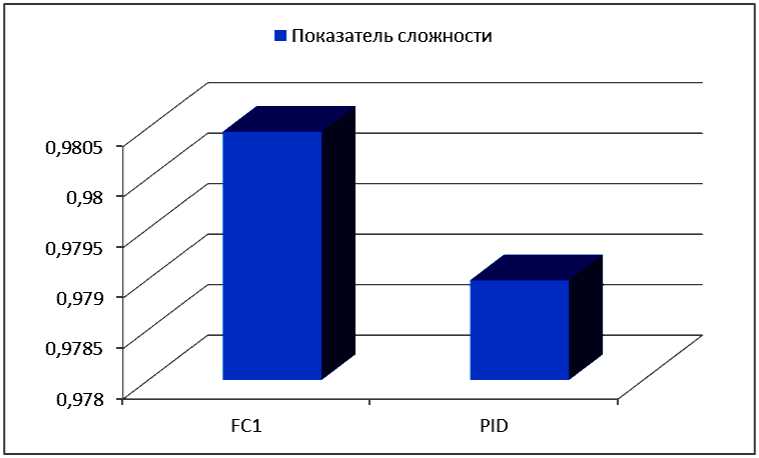
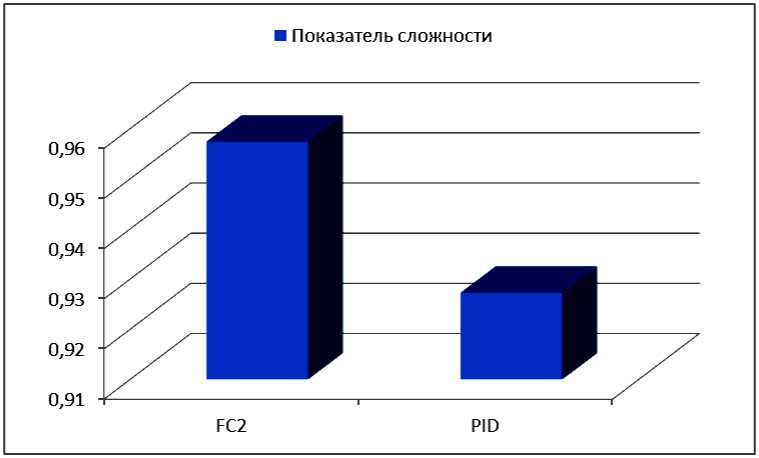
N rL, fXERfc.), и Rf(а)=ПH

k=1

где t^k - моменты времени, k = 1,..., N. N - равно числу точек в управляющем сигнале;

ИIjk(x.), k = 1,..., N - функции принадлежности входных переменных, l - индекс правила в БЗ; символ «П» обозначает операцию нечеткой конъюнкции (в частности, может интерпретироваться как произведение).

«максимальный» критерий: выбрать только те правила, которые удовлетворяют условию: max R^I_fr(t)   TL.                                       (4)

t

Шаг 4: Оптимизация базы правил. С помощью ГА2 оптимизируются правые части правил БЗ. На данном этапе находится решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС). С помощью следующего шага 5 это решение может быть локально улучшено. В данной работе рассматривается возможность подключения реального удаленного ОУ для оптимизации БЗ в режиме реального времени.

Шаг 5: Настройка базы правил. С помощью ГА3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры функций принадлежности входных/выходных переменных (с точки зрения заданной функции пригодности ГА). В данном процессе оптимизации используются различные функции пригодности, выбранные пользователем (шаги 5-1 и 5-2 на рис. 3). На данном этапе имеется возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки (см. шаг 5-3 на рис.3).

Таким образом, результатом проектирования является требуемый тип универсального аппроксиматора в виде НР с оптимальной структурой БЗ.

Рассмотрим модуль удаленного соединения ОБЗ и реального ОУ для оптимизации БЗ.

Удаленное соединение с ОБЗ

Удаленная оптимизация БЗ осуществляется на четвертом этапе проектирования НР (рис. 3). Реализация физической среды соединения предполагает использовать дополнительное оборудование для приема – передачи данных, например радио канал Bluetooth, WiFi или подключение по кабелю, например USB. Предполагается обмен информацией между системой управления и ОБЗ для формирования БЗ (рис. 4).

Рис. 4. Схема соединения настраиваемого устройства и ОБЗ

Рассмотрим подробнее процесс настройки функционирования подобной системы (рис. 5).

Рис. 5 Алгоритм работы удаленной настройки

Система управления считывает показания датчиков и отправляет их на компьютер для последующей обработки. Приняв входные значения, ОБЗ оценивает предыдущее решение (БЗ НР) и осуществляет нечеткий вывод для проверки следующего решения (БЗ НР). Результат нечеткого вывода отправляется на удаленное устройство. После этого, система управления, обработав входные значения, вырабатывает управляющее воздействие. Синхронизация ОБЗ и системы управления осуществляется на основе удаленного устройства (робота).

С этой целью разработана специальная программа (прошивка), реализующая алгоритм, представленный на рис. 5.

Профиль соединения использует последовательный порт. Скорость передачи в нашем случае составляет 115200 бит/с. В процессе функционирования, по COM-порту передаются числа в символьном виде.

Подключение к ОБЗ осуществляется через разработанный плагин. Перед установкой соединения в окне ОБЗ следует выбрать номер СОМ-порта и время проверки одного решения (рис. 6).

Рис. 6. Модуль удаленной настройки для ОБЗ

Проектирование БЗ для НР

Для проведения экспериментов и получения ОС с макета использовался робот, устройство которого представлено на рис. 7:

Рис. 7. Внешний вид и устройство робота

В данной работе используются три датчика для управления:

• 1.    Датчик угла отклонения робота (гироскоп и акселерометр).

• 2.    Датчик положения вала правого колеса робота (энкодер).

• 3.    Датчик положения вала левого колеса робота (энкодер).

На каждое колесо робота установлен энкодер, который используется для подсчета оборотов вращения вала мотора. Это дает возможность стабилизировать положение робота по горизонтальной оси в определенной точке, например в точке включения, не давая роботу отъезжать от этой точки и разворачиваться.

Структура системы управления для данного робота в таком случае выглядит следующим образом:

Рис. 8. Структура системы управления с тремя контурами обратной связи

В качестве управляющего воздействия решено было использовать сумму ПИД-регулятора угла отклонения и П-регулятора на ошибку отъезда каждого колеса. Для проектирования силы управления на каждый мотор используются следующие выражения:

t

• u Right = kpe + ki ^tt + kde + ^kR • zR

t,

• uLeft = kpe ⁺ ki e^tt ^{+ k}de ^{+ k}L • zL

где k – пропорциональный коэффициент на отъезд правого колеса, k – пропорциональный коэффициент на отъезд левого колеса, z – отъезд от точки запуска правого колеса, z – отъезд от точки запуска левого колеса.

Использование удаленной оптимизаций для настройки базы знаний и ГА-ПИД-регулятора для получения ОС позволяет отказаться от математического моделирования объекта управления при проектировании системы управления для конкретной (типовой) ситуации управления. Однако, как было показано в, такие базы знаний не обладают достаточной робастностью.

Для получения ОС с макета используется ГА-ПИД регулятор в режиме реального времени. Отметим, что в [4] коэффициенты ПИД-регуляторов настраивались последовательно, сначала для одного, а потом для второго регулятора. В данной работе все коэффициенты настраивались одновременно.

На рис. 9 и 10 представлен ОС для FC1 и FC2 соответственно.

Спроектируем две базы НР:

• 1.    Получение ОС и удаленная оптимизация в первой ситуации управления (С1) (используется стандартное ковровое покрытие) (FC1).

• 2.    Получение ОС и удаленная оптимизация во второй ситуации управления (С2) (используется резиновый настил) (FC2).

Рис. 9. Обучающий сигнал в ситуации С1. Сверху слева угол отклонения, сверху справа отъезд правого и левого колеса, снизу коэффициенты усиления ГА-ПИД-регулятора

Рис. 10. Обучающий сигнал в ситуации С2. Сверху слева угол отклонения, сверху справа отъезд правого и левого колеса, снизу коэффициенты усиления ГА-ПИД-регулятора

На этапе создания БЗ (рис. 3, шаг 2) полученные ОС используются для формирования лингвистических переменных для входных значений. Результаты первого этапа проектирования представлены на рис. 11 и 12.

В данной работе, в целях создать полную базу знаний не превышающую 100 правил (из-за аппаратных ограничений), было выбрано 3 нечетких множества для пропорциональной и интегральной составляющей, а по 2 для остальных лингвистических переменных. Соответственно полные БЗ состоят из 72 правил.

e

e

e

Zright

Zleft

Рис. 11. Функции принадлежности входных переменных для FC1

e

e

e

Zright

Zleft

Рис. 12. Функции принадлежности входных переменных для FC2

На следующем этапе проектирования БЗ для НР осуществляется формирование и оптимизация количества правил НР (рис. 3, шаг 3). Результат данного этапа представлен на рис. 13.

Рис. 13. Нейронная сеть нечеткого регулятора

Выходные значения на данном этапе равны 0, т.к. их настройка производится на следующем этапе проектирования НР.

Эксперимент

Эксперимент проводился в ситуации управления, соответствующей условиям получения ОС и оптимизации БЗ каждого нечеткого регулятора. Для сравнения результатов был также разработан ПИД-регулятор для каждой из двух ситуаций управления.

Рассмотрим результаты работы FC1 и ПИД-регулятора в ситуации С1 (рис. 14-17):

Рис. 14. Угол отклонения. Ситуация С1

Рис. 15. Отъезд правого и левого колеса от точки запуска. Ситуация С1

Рис. 16. Интеграл квадратичной ошибки угла отклонения. Ситуация С1

Рис. 17. Сумма интегралов квадратичных ошибок отъезда колеса. Ситуация С1

Как видно из графиков, НР не только лучше держит маятник в равновесии, но и не позволяет ему далеко отъезжать от точки запуска.

Рассмотрим результаты работы FC2 и ПИД-регулятора в ситуации С2 (рис. 18-21):

Рис. 18. Угол отклонения. Ситуация С2

Рис. 19. Поведение правого и левого колеса от точки запуска. Ситуация С2

PID ----FC2

Рис. 20. Интеграл квадратичной ошибки угла отклонения. Ситуация С2

Рис. 21. Сумма интегралов квадратичных ошибок отъезда колеса. Ситуация С2

Эксперимент в ситуации С2 также показывает, что нечеткий регулятор, настроенный с помощью удаленного соединения, способен держать низким уровень ошибок со всех трех датчиков.

Анализ качества управления

Для оценки качества процесса управления используем сложность управления. Сложность управления (P) характеризует способность системы управления эффективно расходовать энергетический и технический ресурс (A) системы. В случае реализации сложного управления, износ оборудования и затраты энергии будут велики. Сложность управления (рис. 22 и 23) рассчитывается в виде:

P = 1-

V T„01

A

dt

; A = (const).

Рис. 22. Сложность управления для регуляторов ситуации С1

Рис. 23. Сложность управления для регуляторов ситуации С2

Как видно нечеткие регуляторы FC1 и FC2 обладают высоким уровнем показателем сложности, что характеризует их работу как более эффективную.

Выводы

Результаты проделанных исследований показывают, что:

удаленная оптимизация БЗ вместе с ГА-ПИД регулятором позволяют строить ИСУ без использования математического моделирования;

ОБЗ позволяет настраивать сложные системы управления с большим количеством контуров управления. Количество входных переменных и размер получаемой БЗ ограничивается лишь аппаратными характеристиками компьютера и ОУ;

дистанционное соединение позволяет оптимизировать БЗ в определенных (типовых) условиях функционирования, тем самым создавать множество БЗ с высоким качеством управления для различных ситуаций управления.