Интеллектуальные образовательные технологии в учебном процессе

Компетентностный подход как основа, заложенная в федеральных

государственных и международных образовательных стандартах [1]-[3], а также стандартах, самостоятельно устанавливаемых вузами [4],[5], направлен на формирование у обучаемых универсальных, общепрофессиональных и профессиональных компетенций, необходимых для их успешной профессиональной деятельности.

Достижение целей обучения требует постоянной модернизации рабочих программ изучаемых дисциплин с использованием методологических подходов, развиваемых в рамках отечественных и международных проектов типа [6]-[10], а также разработки и внедрения в учебный процесс электронных образовательных ресурсов. К последним можно отнести разработки ННГУ [11]-[16].

Обучение - это интеллектуальный процесс, конкретный сценарий развития которого (рабочий сценарий) априори не известен. Он рождается непосредственно в процессе обучения и зависит от интеллектуальных способностей обучаемого (способностей воспринимать окружающий мир, осознавать воспринятое, делать обобщения, проводить аналогии и т.п.), уровня его предварительной подготовки, заложенной в нем психологической основы, условий обучения и многого другого.

Интерактивная форма обучения [17], в отличие от формата обычной лекции

(по типовому сценарию, спланированному преподавателем, с несущественными отклонениями на возникающие вопросы по текущему материалу), предполагает активное участие обучающихся в образовательном процессе не только в плане усвоения изучаемого материала, но и в направлении формирования рабочего сценария обучения, максимально адаптированного к их индивидуальным особенностям .

Активность в этом плане может обеспечиваться выполнением следующих действий:

• •    самостоятельное предварительное ознакомление с материалом, планируемым преподавателем для изучения на очередном занятии (источником может быть учебное пособие с материалом лекций или оболочка интеллектуальной

обучающей среды [18],[19], настроенная через формализм базы знаний на данную дисциплину);

• •    подготовка вопросов (по теме предстоящего занятия и, возможно, уже пройденным темам), направленных на углубление понимания материала, перспектив его использования в дальнейшем образовательном процессе и практического применения в конкретных предметных (проблемных) областях;

• •    участие в обсуждении на занятии поднятых вопросов, в том числе и вопросов преподавателя, направленных на внесение в процесс обучения необходимых корректив и формирование у него представления о степени и глубине усвоения материала обучающимися.

Выполнение указанных действий способствует формированию рабочего сценария, наилучшим образом адаптированного к наиболее активным участникам процесса обучения.

Такая форма обучения способствует рациональному использованию времени аудиторных занятий на усвоение материала лекций и попытки применения его для решения конкретных проблем. Рабочие сценарии таких занятий могут приводить к возникновению дискуссий, разработке методом мозгового штурма конкретных проектов, способствующих привитию навыков работы в коллективе.

Особую роль в организации интерактивных форм обучения приобретают современные компьютерные технологии, базирующиеся на моделях и методах искусственного интеллекта [20]. В разряд наиболее актуальных выходят проблемы создания оболочек интеллектуальных обучающих сред, способных настраиваться на различные предметные области и генерировать индивидуальные сценарии обучения, адаптированные к уровню подготовки, интеллектуальным способностям и психологическим особенностям обучаемых.

Предпринятые в работах [18],[21] попытки адаптации к условиям применения в учебном процессе оболочки универсальной гибридной системы интеллектуально й поддержки процессов принятия решений [22],[23] выявили ряд специфических особенностей интеллектуальной поддержки процесса обучения, базирующейся на нечеткой логике принятия решений:

• -    невозможность формирования графа решений с указанием коэффициентов уверенности для вершин выводов, значения которых определяются не только опытом и интуицией эксперта (преподавателя), но и индивидуальными особенностями обучаемого;

• -    как следствие, трансформация графа решений в набор нечетких продукционных правил без указания значений коэффициентов уверенности правил;

• -    возможность формирование продукционных правил в законченном виде (с указанием их коэффициентов уверенности) только непосредственно в процессе обучения после выдачи связанных с ними фрагментов изучаемого материала и тестирования уровня их усвоения обучаемым;

• -    как следствие, нереальность анализа альтернатив в развитии сценария обучения с использованием стратегии поиска в ширину.

Отмеченные особенности интеллектуальной поддержки процесса обучения потребовали от авторов более глубокого анализа и пересмотра базовых принципов реализации концепции гибридной интеллектуальной обучающей среды, изложению результатов которых посвящена данная статья.

Теоретическая часть

Согласно отправной концепции процесс обучения представлен в пространстве состояний S и формируется в виде последовательности событий e1, e2, ..., ek, каждое из которых (например, событие ei) связано с выводом на терминал неделимого логически законченного фрагмента изучаемого материала и возможным тестированием уровня его усвоения li обучаемым. Уровень усвоения оценивается по непрерывной шкале [0,1] как усредненный результат тестирования (при отсутствии фазы тестирования значение li по умолчанию принимается равным 1).

Событию e i в базе знаний аналитической составляющей интеллектуальной обучающей среды поставлено в соответствие нечеткое продукционное правило, антецедент которого определяет условия его активации в виде перечня имен событий (с их исходами ), без активизации которых событие e i невозможно. Консеквент правила фиксирует имя события e i , оставляя незаполненным поле значения его исхода . С продукционным правилом связан фрагмент изучаемого материала, представленный при наличии фазы тестирования на двух уровнях детализации ( компактном и детальном ), а также тесты, определяющие уровень усвоения материала l i . Под исходом r i события e i понимается результат нечеткой операции логического следования (нечеткой импликации) уровня его усвоения l_i из исходов событий, указанных в антецеденте правила. Исход события r i интерпретируется как коэффициент уверенности усвоения материала события e i . Имя каждого активизированного события и значение его исхода (коэффициента уверенности) фиксируются в рабочей памяти системы, меняя ее состояние .

Для описания знаний эксперта на инфологическом уровне использован формализм графа решений [20], позволяющий компактно и наглядно представить нечеткую логику рассуждений эксперта до уровня нечеткости, обусловленной индивидуальными особенностями обучаемых.

Граф решений - это ориентированный помеченный граф с вершинами двух типов:

• •    вершины условий ( типа «овал» ), из которых могут исходить несколько ребер, соответствующих различным исходам указанных в них событий;

• •    вершины выводов ( типа «прямоугольник» ), разрывающие или завершающие непрерывные цепочки вершин-овалов, определяющих необходимые условия активизации событий, указанных в вершинах вывода (промежуточного или окончательного, соответственно).

Таким образом, вершина вывода содержит имя события, востребованного ситуацией, определяемой предшествующей непрерывной цепочкой вершин условий, возможно начинающейся с вершины промежуточного вывода. Следует заметить, что на этапе формирования графа решений возникают проблемы с заданием коэффициентов уверенности для вершин выводов, значения которых зависят не только от опыта и интуиции эксперта (преподавателя), но и от индивидуальных особенностей обучаем ых, вносящих свой весом ый вклад в нечеткость рассуждений. Поэтому вычисление этих значений, трансформируемых в коэффициенты уверенности продукционных правил, может быть осуществлено только в ходе обучения после выдачи связанных с ними фрагментов изучаемого материала и тестирования уровня их усвоения. Фактически для каждого обучаемого непосредственно в процессе обучения формируется индивидуальный набор нечетких продукционных правил со всеми коэффициентами уверенности, выстраиваемый в логическую цепочку рассуждений - рабочий сценарий обучения.

Для описания структурированных с целью сужения пространства поиска знаний может использоваться не один, а несколько графов решений.

На рисунке 1 приведен пример фрагмента графа решений, представляющего нечеткую логику формирования сценария обучения на инфологическом уровне для дисциплины «Схемотехника и организация вычислительных систем» с использованием (для компактности) следующих имен событий:

• е 1 - введение понятия вычислений;

е₂ - введение понятия вычислительной системы (ВС);

е₃ - введение понятия архитектуры ВС;

е₄ - многоуровневое представление архитектуры ВС;

е₅ - базовый естественно-математический уровень.

Правила, сгенерированные по фрагменту графа решений, представленному на рисунке 1, выглядят следующим образом:

ЕСЛИ Событие е 1 не активизировано

ТО Активизировать компактное представление	события е1
ЕСЛИ Событие е1 активизировано И Событие е2 не активизировано ТО Активизировать компактное представление	события е2
ЕСЛИ Событие е 1 активизировано И Событие е2 активизировано И Событие е3 не активизировано ТО Активизировать компактное представление	события е 3
ЕСЛИ Событие е 1 активизировано И Событие е2 активизировано И Событие е3 активизировано ТО Активизировать компактное представление	события е 4

ЕСЛИ Событие е 4 активизировано

И Исход события е₄ в интервале [0, r i )

ТО Активизировать детальное представление события е 4

ЕСЛИ Событие е 4 активизировано

И Исход события е₄ в интервале [ r i , п )

ТО Активизировать компактное представление события е 4

ЕСЛИ Событие е 4 активизировано

И Исход события е₄ в интервале [ п ,1]

И Событие е₅ не активизировано

ТО Активизировать компактное представление события е₅

ЕСЛИ Событие е₄ активизировано

И Исход события е₄ в интервале [ Г 2 ,1]

И Событие е₅ активизировано

И Исход события е₅ в интервале [0, r i )

ТО Активизировать детальное представление события е 5

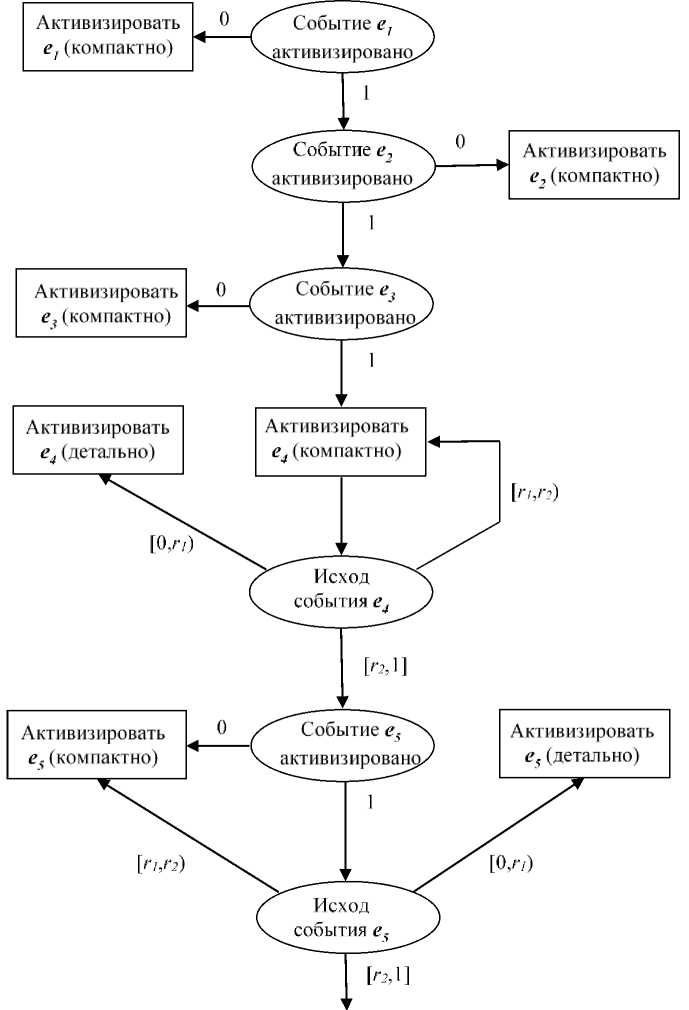
Рис. 1. Фрагмент графа решений, отражающего нечеткую логику формирования сценария обучения на инфологическом уровне

ЕСЛИ Событие е₄ активизировано

И Исход события е₄ в интервале [ п ,1]

И Событие е₅ активизировано

И Исход события е₅ в интервале [ r i , Г 2 )

ТО Активизировать компактное представление события е₅

Помимо набора продукционных правил (для аналитической составляющей обучающей среды) подсистема приобретения знаний формирует как основу синтетической составляющей нейронную сеть прямого распространения (многослойный персептрон), эквивалентную по логике «рассуждений» исходному графу решений.

Алгоритм трансформации графа решений в эквивалентную нейронную сеть функционирует по следующим правилам:

• •    каждой вершине вывода ставится в соответствие свой нейрон, на выходе которого формируется исход связанного с ним события после его активизации (в качестве активационной функции нейрона выступает нечеткая операция логического следования уровня усвоения материала события из исходов событий, поступивших на его входы);

• •    каждой вершине условия сходящейся к вершине вывода непрерывной цепочки вершин-овалов, а также вершине промежуточного вывода, с которой может начинаться цепочка, ставится в соответствие входная ветвь нейрона;

• •    нейроны располагаются по слоям согласно правилу: каждый нейрон последующего слоя должен иметь входные связи только с нейронами предшествующих слоев и хотя бы одну входную связь с каким -нибудь нейроном предыдущего, смежного с ним слоя;

• •    каждому выходу из вершины условия графа решений ставится в соответствие нейрон сенсорного слоя, ретранслирующий входной сигнал на нейроны последующих слоев в соответствии со структурой сгенерированной нейронной сети ;

• •    сигналы выходов всех нейронов промежуточных слоев выводятся на нейроны моторного слоя, использующие максимум в качестве активационной функции.

Нейронная сеть, построенная для приведенного выше графа решений, изображена на рисунке 2, где использованы следующие обозначения сигналов:

• r pi, i - сигнал не активизированного события e i в такт p ;

r pi, 2 - сигнал активизированного события e i в такт p ;

r pi, з - значение исхода события e i в интервале [0, r i ) в такт p ;

r pi, 4 - значение исхода события e i в интервале [ r i , Г 2 ) в такт p ;

r pi, 5 - значение исхода события e i в интервале [ Г 2 ,1] в такт p ;

rpi,6 - принимаемое по умолчанию единичное значение исхода события ei, не предусматривающего фазу тестирования, в такт p;

a^p i, c - сигнал активизации компактного представления события e i в такт p+1 ;

a^p i, d - сигнал активизации детального представления события e i в такт p + 1 ;

r i , r 2 - настроечные параметры оболочки.

В рассматриваемой версии оболочки гибридной интеллектуальной обучающей среды схема трансформации графа решений в эквивалентную по логике «рассуждений» нейронную сеть прямого распространения доведена до конструктивного вида. Определены активационные функции нечетких нейронов, обеспечивающие потактовое управление процессом обучения и фиксацию его текущего состояния в рабочей памяти обучающей среды. Предусмотрено запоминание последовательности меняющихся в процессе обучения состояний для обеспечения возможности возврата к ним с целью повторения пройденного материала.

r^p 1, 1

r^p 1, 2

r^p 2, 1

r^p 2, 2

r^p 3, 1

r^p 3, 2

r^p 4, 3

r^p 4, 4

r^p 4, 5

r^p 5, 1

r^p 5, 2

r^p 5, 3

r^p 5, 4

_а p+1_{1, c}

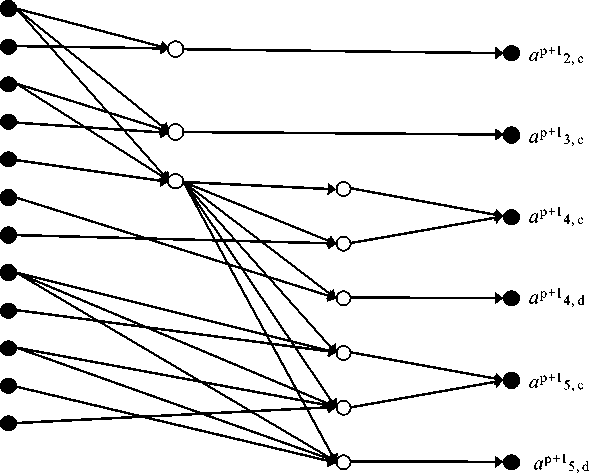
Рис. 2. Нейронная сеть, сформированная по графу решений

Следует заметить, что все функции потактового формирования рабочего сценария обучения полностью обеспечиваются структурой нейронной сети, не требуя управления какими-либо ее параметрами.

Реализация

Модифицированная версия оболочки гибридной интеллектуальной обучающей среды имеет в своем составе:

• •    исходно пустую базу знаний;

• •    подсистему приобретения знаний;

• •    механизм нечеткого логического вывода;

• •    интеллектуальный интерфейс.

База знаний объединяет в себе долговременные знания о предметной области в виде набора нечетких продукционных правил ( базу правил ), оперативные данные рабочей памяти , фиксирующей состояние обучающей среды, а также информационный материал событий и завершающих их тестов, привязанный к продукционным правилам.

База правил представлена четырьмя массивами:

• •    массив имен событий антецедентов правил ;

• •    массив значений исходов событий антецедентов правил ;

• •    массив имен событий консеквентов правил;

• •    массив значений исходов событий консеквентов правил.

В массиве имен событий антецедентов правил под каждое правило отведено по n элементов в предположении, что антецедент любого правила может включать не более n имен событий ( n – настроечный параметр оболочки). Аналогичную структуру имеет массив значений исходов событий антецедентов правил .

В массиве имен событий консеквентов правил , как и в массиве значений исходов событий консеквентов правил , под каждое правило отведено по одному элементу.

Массивы имен событий антецедентов и консеквентов правил строятся априори на основании графа решений, массивы значений исходов событий формируются в процессе обучения с использованием результатов тестирования. Таким образом, по окончании сеанса обучения база правил представляет собой набор четких продукционных правил, который можно использовать для повторной прокрутки сгенерированного рабочего сценария, исключив из него процедуры тестирования.

Рабочая память оболочки представлена таблицей событий , каждая строка которой имеет два поля. Первое определяет имя события, которое может входить в антецеденты правил. Второе фиксирует значение исхода события, вычисленное при его активизации.

Перед началом логического вывода, заполнены только первые поля всех строк таблицы, т.е. дан перечень имен всех событий, характеризующих состояние процесса обучения. Заполнение первого поля таблицы осуществляется на этапе инициализации обучающей среды путем просмотра массивов имен событий антецедентов и консеквентов правил. Затем в процессе идентификации и срабатывания правил заполняются вторые поля таблицы значениями исходов событий, получаемыми после тестирования усвоения материала или принимаемыми по умолчанию за 1 в несложных ситуациях.

Подсистема приобретения знаний , принимая на вход описание графа решений, формирует набор нечетких продукционных правил для аналитической составляющей обучающей среды. Для синтетической (нейросетевой) составляющей она трансформирует граф решений в эквивалентную (по логике «рассуждений») нейронную сеть прямого распространения.

Механизм вывода выполняет функции аналитического ядра интеллектуальной обучающей среды, осуществляющего построение прямой (управляемой антецедентами) логической цепочки рассуждений. Реализуемая при этом стратегия поиска во многом зависит от индивидуальных особенностей обучаемого.

Подсистема объяснения обеспечивает пользователя возможностью отслеживать динамику развития сценария обучения, оценивая текущий уровень своей компетентности и при необходимости внося в процесс обучения определенные коррективы (например, пройти повторно на компактном или детальном уровне с последующим тестированием некоторую цепочку событий).

Интеллектуальный интерфейс объединяет в себе лингвистические, информационные и программные средства взаимодействия пользователя (обучаемого), инженера по знаниям (аналитика) и эксперта с соответствующими компонентами обучающей среды (пользователя с механизмом логического вывода, подсистемой объяснения, и нейронной сетью, аналитика и эксперта с подсистемой приобретения знаний). Они ориентированы на неподготовленного пользователя, обладают способностью настраиваться на его терминологию и создавать по возможности комфортные условия для работы в системе.

Анализ и оценка разработки

Разработанная оболочка гибридной интеллектуальной обучающей среды способна через формализм графа решений, как средство описания знаний на инфологическом уровне, настраиваться на различные предметные (проблемные) области. Генерируя индивидуальный (адаптированный к уровню подготовки, интеллектуальным способностям и психологическим особенностям пользователя)

сценарий освоения материала, она может эффективно выполнять функцию компьютерной поддержки интерактивной формы учебного процесса на этапах самостоятельной работы обучаемых.

Заключение

Данная статья представляет модифицированную версию оболочки гибридной интеллектуальной обучающей среды, отличающуюся более глубоким анализом и пересмотром базовых принципов реализации с ориентацией на использование нечеткой продукционной логики представления знаний экспертов, позволяющей повысить гибкость функционирования системы в целом и максимально адаптировать процесс обучения к индивидуальным особенностям обучаемого.

В настоящее время модифицированная версия оболочки проходит тестовую эксплуатацию на примере дисциплины «Интеллектуальные информационные системы» на кафедре Информатики и автоматизации научных исследований ННГУ.