Intelligent training algorithm for artificial neural network EEG classifications

The electroencephalogram (EEG) is a low amplitude signal generated in the brain, as a result of information flow during the communication of several neurons. Hence, careful analysis of these signals could be useful in understanding many human brain disorder diseases. One such disease topic is epileptic seizure identification, which can be identified via a classification process of the EEG signal after preprocessing [1].

Epilepsy is a major neurological diesis occurring in the brain characterized by recurrent seizures [1]. The abnormal electrical activity of brain cells caused temporary variation in brain functions which is known as epileptic seizures. Routinely EEG signal is used to diagnose epilepsy clinically [2]. EEG is an important tool used to identify and analyze human epileptic seizures activity. Traditional epileptic seizure diagnosis relies on verbose visual screening by neurologists from EEG recording. Recently, there are many automatic systems helping the neurologists to quickly find interesting segments of seizure detection [3].

Over many years for various biomedical signal analyses neural networks NN have been very widely used since they split the signals efficiently for decisionmaking. Over the years there are several other architectures of NN model that have been used such as Multilayer Perceptron Neural Network (MLPNN), Radial Basis Function (RBF), Recurrent Neural Network (RNN), etc. [4]. In addition to these methods, heuristic optimization algorithms are used to increase the speed of these methods. Particle swarm optimization (PSO) as a heuristic optimization method has been successfully applied to train ANNs. It has been proposed to update network weights because of its easy implementation and realization [5].

II.    Related Works

Up to now, several techniques have been proposed on the classification of EEG signals in different literature and diverse classification accuracies have been reported in the last decade for the EEG epileptic data. Brief descriptions of the previous research are provided below.

Guler et al. [8] assessed the diagnostic accuracy of recurrent neural networks (RNNs) using Lapunov exponents trained with the Levenberg-Marquardt algorithm on the EEG epileptic database. Jahankhanni et al. [9] used a wavelet transform for feature extraction and neural networks for EEG signal classification on the EEG epileptic database. Polat et al.[10] used an approach for the classification of epileptiform EEG using a hybrid system based on a decision tree classifier and the fast Fourier Transform. Guo et al. [11] introduced relative wavelet energy and artificial neural networks for the classification of EEG signals. Chandaka et al. [12] also utilized a cross-correlation aided SVM classifier for classifying EEG signals of the healthy subjects and epileptic patients. Vahid Fathi et al.[13] have proposed a novel PSO-OSD algorithm to improve the RBF learning algorithm in real time applications for EEG classification.

III.    Methods

This section explains extensively on the overall processes that were implemented for this work. It consists of EEG data collection, pre-processing and filtering, feature extraction and normalization, and finally the development of brain dieses classification model using ANN as illustrated in Figure 1.

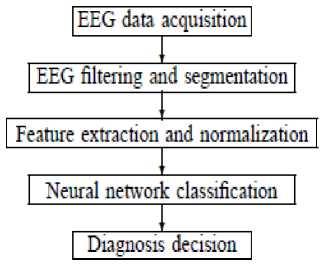
Fig.1. Proposed system block diagram

• A.    Data acquisition

• 23.6 second and 4096 sampling points. The eye movement artifacts have been manually removed by visual inspection. Set A and B are carried out from healthy subjects with open eyes and closed eyes respectively. Set C and D segments recorded within an epileptogenic zone which contains only activities measured during free interval seizure (interictal period). Set E contains only seizure activity segments (ictal period). All EEG signals were sampled at a sampling frequency of 173.6 Hz.

In our experiment, we foster the data set, which is widely adopted by previous researchers [8-10], from the University of Bonn, German [14]. It includes five sets (A – E). Each set has 100 single channel EEG segments over

In our study, EEG signals from sets A, C, and E have been used to classify the healthy, interictal seizures, and ictal seizures.

• B.    Filtering

EEG signal is usually contaminated by different noise sources. This noise needs to be removed before analyzing the signal. plenty of noise removal techniques are implemented. Brain waves are classified according to frequency as Delta (0.1 – 4 Hz), Theta (4 – 8 Hz), Alpha (8 – 12 Hz), Beta (12 – 30 HZ), and Gamma (> 30 Hz) [15]. In our study, we propose FIR bank filter to denoise the signals as shown in figure 2. Also, the FIR bank filter used to split the raw EEG data signals into the brainwaves frequency bands. The frequency bands extracted and carried out in our study are delta, theta, alpha, and beta (0.1 – 30Hz) only since EEG signals do not have any useful frequency components above 30Hz [16].

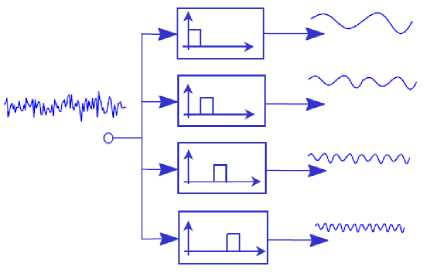
Fig.2. FIR bank filter

• C.    Feature extraction

Feature extraction is the process of transforming the input data into a set of features. In order to perform the desired task optimally, the feature set must extract the relevant information from the input data. In our study, the energy distribution for each frequency bands is used for feature extraction. According to Parseval's theorem, the energy of original signal can be partitioned at different bands or levels and mathematically can be represented as [16].

ED ij = Z 7=i lOi;l 2                   (1)

Where N is the number of samples or number of volunteers, i= (1  – 5) which represent the signal frequency bands. Figures 3 illustrate the energy band of set A, set C, and set E. These signals are plotted according to feed the input sets to FIR bank filter and then calculate the energy for each frequency bands using equation (1). The filter and the energy distribution calculation is simulated and implemented using MATLAB 2013 software environment.

• D.    Classification

Multi-layer Perceptron (MLP) neural network has been implemented to classify EEG signal by many researchers [17-19]. MLP networks are the most popular feed forward supervised artificial neural networks that map set of input data to a set of appropriate output. MLP taking advantage of supervised learning technique called back propagation trains the network. Any MLP has an input layer, output layer, one or more hidden layers. Each layer or neuron inputs are connected to an output of previous layer or neurons whereas output layer neurons determine input class. Using more than one hidden layer

(processing layer) may improve the network performance but may lead to converging to local minima. Usually, one processing layer is sufficient to classify the input data [20]. Each layer consists of one or multiple neurons depending on the solving problems. Each neuron realizes a function of weighted summation and special linear or nonlinear activation function. The connection between neurons called weight. Adjusting these weights is the way to solve the problem which is identified as training or learning process. When the number of neurons in the hidden layer has been selected, the network weights must be optimized to minimize the mean square error made by the network. The fully connected MLP neural network with the input layer, output layer, and one hidden layer is illustrated in figure 4. As shown in the figure each connection line represents a weight that must be adjusted to a suitable value in order to minimize the mean square error [21].

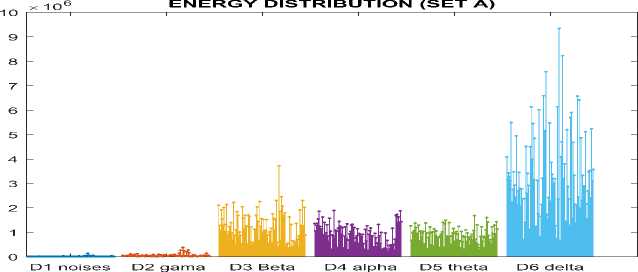
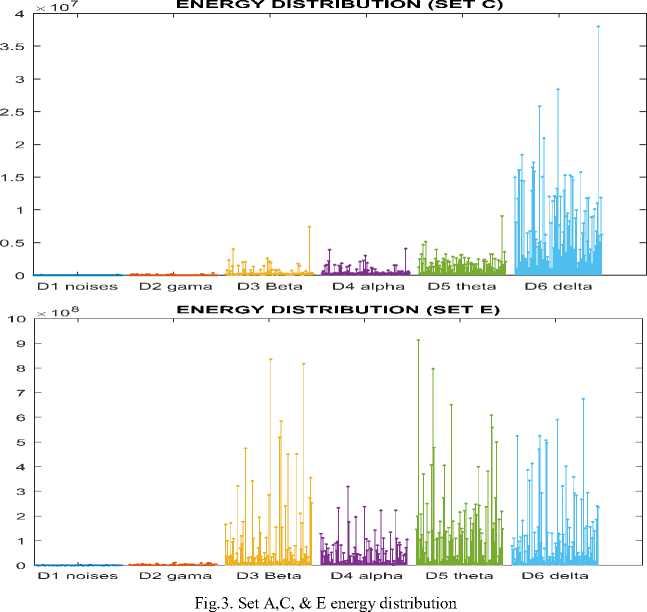
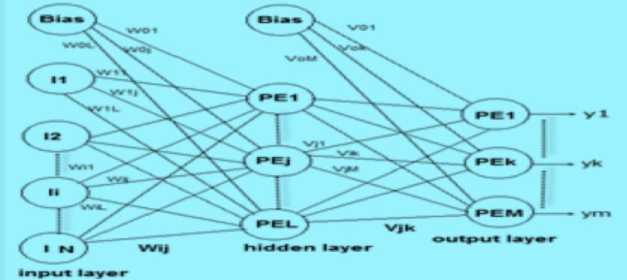
Fig.4. Fully connected single hidden layer ANN

IV.    Ann Weights Optimization Algorithms

The most important issue related to neural networks is how to learn the network to give the right solution with the most optimized weights. Training of neural network is the process of adjusting the weights of the network. One of the most popular training algorithms is the Back Propagation Algorithm (BPA), this algorithm has been extensively used for the network training purpose. BPA seems to be suffering from multiple problems, such as easily fall into local minima and its low convergence speed. Many attempts have been made to improve the performance of BPA, while other just used Evolutionary Algorithms (EAs) to replace BPA in the training phase [22].

EAs are generic population-based meta-heuristic optimization algorithms. Most of the EAs were inspired by natural phenomena or living creatures. EAs use mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Each individual in the population is a candidate solution. Fitness function determines the quality of the candidate solutions. Each EA has its global and local search mechanism to guide population towards an optimum or near optimum solution by iterations. The general rules used to optimize neural network weights using EAs can be summarized as [23]:

• •    Consider the weights vector of the neural network as a single population particle in the swarm.

• •    Each swarm is a matrix consists of population size (popsize) rows and a number of weights (ndim) columns.

• •    Initialize the swarm matrix randomly according to the limits of the search space.

• •    Evaluate the Mean Square Error (MSE) for each particle, and evaluate the best particle and its location in the swarm matrix.

• •    Consider the particle with the minimum MSE is the global best (gbest) solution and each other is a local solution ( lbest ).

• •    Run the optimization algorithm to modify each particle lbest and the global gbest .

• •    Check if the iteration reached its maximum value

or the MSE is at its minimum value.

• •    Repeat till one of the above conditions achieved.

This research implements and compares the performance of four evolutionary population-based algorithms using MATLAB 2013 for training neural networks. Some of these algorithms are very well known and have been previously used for training neural network such as Practical Swarm Optimization (PSO). Other algorithms are recently used such as Artificial Bee Colony (ABC), Cuckoo Search Optimization (CSA), and Grass Root Optimization (GRO). Sandeep et al. [24] have proposed a modified PSO algorithm to train the Radial Basis Function Neural Network (RBFNN) more efficiently to classify the epileptic brain seizures. Akkar et al. [25, 26] have proposed a GRO algorithm to control mobile robot path tracking; also they conclude that GRO has faster convergence with a minimum number of iterations than other ten compared algorithms.

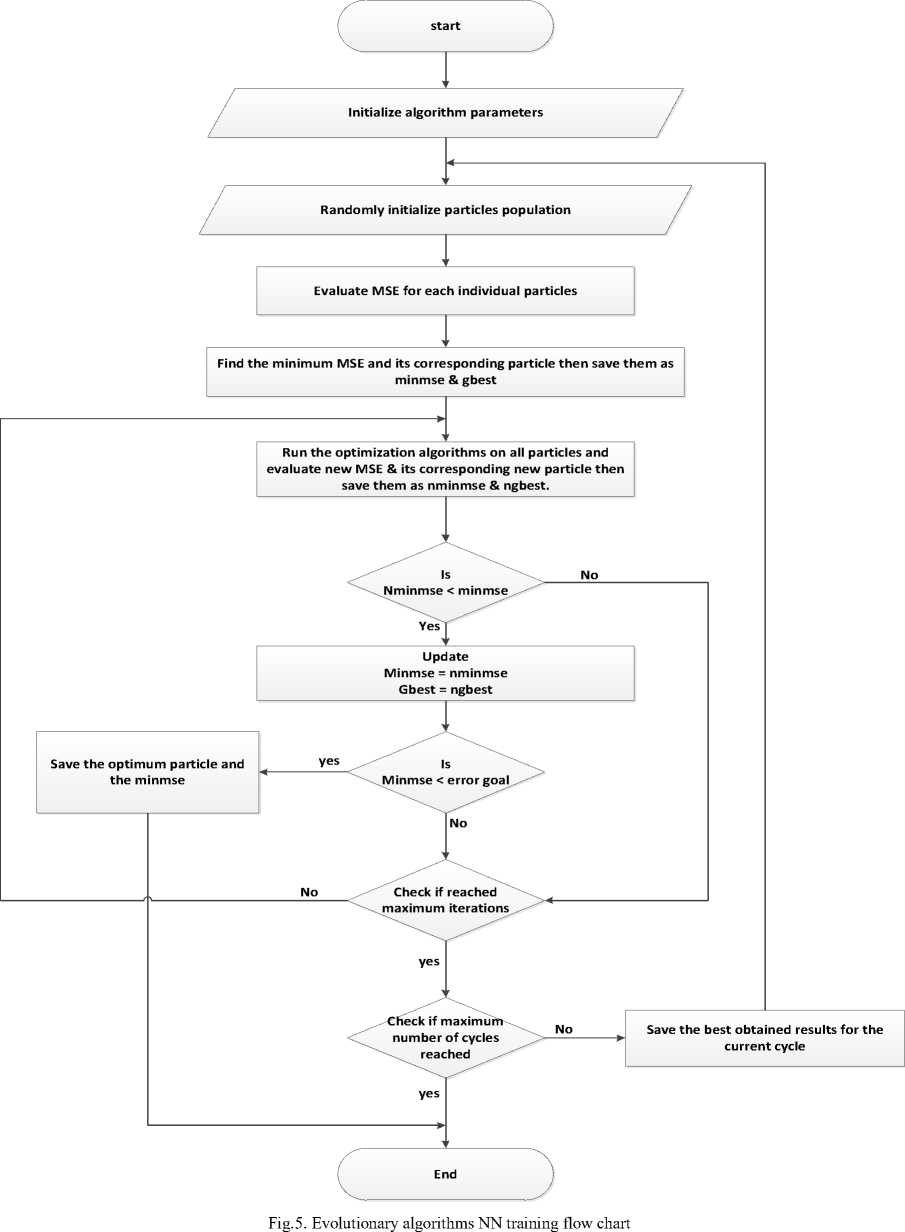
The NNs general training flow chart with populationbased evolutionary algorithms is shown in figure 5.

V. Experiments and Results

There are three sets of data (A, C, and E). Each set contains 100 signals over 23.6 second and 4096 sampling points sampled at 173.6 Hz. Each set has been filtered and distributed to five bands delta, theta, alpha, beta, and gamma. The energy distribution of these bands has been extracted, and then these extracted data have been fed into the neural network. The network has 5 input neurons, 3 hidden neurons, and 2 output neurons.

We have used pure linear activation function for hidden and output layer neurons. Each 100 data sample has been divided into 75 training samples and 25 testing samples. This paper has considered four experiments for ANN training using mentioned algorithms to classify the EEG signal.

Recording the classification rate (CR), average training mean square error (MSE- TR), average testing mean square error (MSE- TS), average error between MSE of training and testing datasets (MSE- ERR), the processing time (T) in seconds, and maximum iteration (Max-it) for the four experiments.

The network has been tested with the following parameters: no. of hidden neurons(L)=3, neuron bias(B)=1, no. of population search(POP)=10, space search limits(LIM)=2, and maximum iteration=100). This network performance with these parameters is used as a reference to compare it with the following experiments as illustrated in table 1.

It is clear from table 1 that GRO has gotten the highest 100% CR with relatively low MSE-TR, MSE-TS, MSE-ERR, low processing time, and requires minimum iteration to reach to an optimum solution. While PSO has gotten the smallest CR (83.56%) with lower processing time and lower MSE-ERR but requires maximum iteration to optimum the solution.

• ❖ Experiment 1:

In this experiment, we study the effect of changing the hidden layer neurons on the network performance for the four algorithms. Table 2 illustrates the ANN performance results for 3 states (L=2, L=8, L=16).

Comparing these results with the reference table we can conclude that:

• 1.    For GRO algorithm the CR still the highest 100%, and enhanced MSE for all changes. While the time was increased when L decreased. Increasing L produce decreasing in processing time except for increasing L to 16 neurons make the time increased. Decreasing L needs more iteration to reach the optimum solution.

• 2.    For ABC algorithm, decreasing L enhanced MSE, CR, processing time, and need the lowest iteration.

• 3.    For CSA algorithm, there was not any improvement in network performance with changing L.

• 4.    For PSO algorithm, MSE, CR, processing time was enhanced when L=2 & 8, while these

parameters were decreased when L=16.

• ❖ Experiment 2:

Comparing these results with the reference (B=1) we can conclude:

• 1.    GRO algorithm still has got highest CR 100%. For B=0.8, MSE & processing time was improved with minimum iteration. For B=0.5, MSE was improved while processing time was retarded with more iterations.

• 2.    There were small improvements in ABC algorithm performance with changing neuron bias to 0.5. While the performance parameters were decreased with B=0.8. But it requires less processing time in both cases.

• 3.    For CSA algorithm, CR relatively still the same, there was a small improvement in MSE & required time for both cases.

• 4.    For POS algorithm, MSE & time relatively still the same, there was an improvement in CR.

• ❖ Experiment 3:

Comparing these results with the reference results (table 1) we can conclude:

• 1.    For GRO, increasing number of population search will improve MSE but with more iteration and more processing time. There was no relatively

• 2.    For ABC, decreasing POP will improve MSE, CR & processing time. There was small performance improvement increasing POP.

• 3.    For CSA, there was no relative improvement in NN performance with changing a number of population search.

• 4.    For PSO, increasing pop will improve CR, MSE & less processing time with less iteration. There was no relative improvement decreasing it.

performance improvement when decreasing it.

• ❖ Experiment 4:

In this experiment, we study the effect of space limits for algorithms search on the network performance. Table 5 shows the ANN performance for (LIM=10, LIM=20).

Comparing these results with the reference one shown in table 1 we conclude:

• 1.    For GRO, increasing LIM to10 will produce little performance improvement. Increasing more requires more processing time and more iteration to optimum the solution.

• 2.    For ABC, increasing LIM will retard the performance and reduces the classification rate to 0%.

• 3.    For CSA, increasing LIM will retard the ANN performance parameters.

• 4.    For PSO, increasing LIM also will retard the ANN performance and reduces the classification rate to 0%.

VI. Conclusion

The results have shown that the GRO performance has gotten highest classification rates 100% with a minimum number of iterations over the four experiments than other compared algorithms.

From the experiments we can conclude:

• 1.    Using too many neurons in the hidden layer could result in an over fitting problem. Therefore some compromise must be reached between too many and few neurons in the hidden layer.

• 2.    Decreasing neuron bias little bit will produce minimum improvement in performance parameters except ABC algorithm needs to more bias reduction.

• 3.    Increasing number of population search will improve the classification rate but with more processing time.

• 4.    The ANN performance parameters will be retarded when increasing the space limits of algorithm search.

Table 1. Network algorithms performance (reference)

network performance at (L=3, B=1, POP=10, LIM=2)

ALG.	MSE-TR	MSE-TS	MSE-ERR	CR%	T(SEC.)	MAX-it
GRO	0.014752602	0.009834469	0.004918133	100%	0.1705709	10
ABC	0.080803	0.076898	0.003905	90.67%	0.237751	100
CSA	0.049238	0.04147	0.007498	98.22%	0.204564	100
PSO	0.107543	0.105559	0.001984	83.56%	0.165719	100

Table 2. Network algorithms performance (experiment 1)

	ALG.	MSE-TR	MSE-TS	MSE-ERR	CR%	T(sec.)	MAX-it
L=2	GRO	0.01195	0.01504	-0.00309	100%	0.34883	41
	ABC	0.03509	0.03985	-0.0047	100%	0.1311	64
	CSA	0.08127	0.08538	-0.0041	89.33%	0.14918	100
	PSO	0.07593	0.08499	-0.00906	89.78%	0.1215	100
L=8	GRO	0.007945	0.008485	-0.0005	100%	0.051874	2
	ABC	0.86583	1.004548	-0.1387	34.22%	0.185191	100
	CSA	0.073595	0.09282	-0.0192	97.33%	0.168304	100
	PSO	0.023531	0.032184	-0.0087	100%	0.10766	81
L=16	GRO	0.020849	0.019343	0.00151	100%	0.68148	32
	ABC	1.497217	1.235105	0.26211	31.11%	0.19751	100
	CSA	0.185517	0.174933	0.01058	69.33%	0.19098	100
	PSO	0.254977	0.254267	0.00071	70.67%	0.1515	100

Table 3. Network algorithms performance (experiment 2)

	ALG.	MSE-TR	MSE-TS	MSE-ERR	CR%	T(sec.)	MAX-it
B=0.8	GRO	0.02959	0.027971	0.00162	100%	0.054813	3
	ABC	0.360529	0.207229	0.1533	68%	0.177287	100
	CSA	0.032043	0.022409	0.009634	98.67%	0.152466	100
	PSO	0.098595	0.096442	0.002152	90.67%	0.159342	100
B=0.5	GRO	0.005437	0.007173	-0.007173	100%	0.396994	31
	ABC	0.061153	0.070631	-0.00948	92.89%	0.179606	100
	CSA	0.037943	0.043997	-0.00605	96.44%	0.156822	100
	PSO	0.093813	0.121625	-0.02781	86.67%	0.122585	100

Table 4. Network algorithms performance (experiment 3)

	ALG.	MSE-TR	MSE-TS	MSE-ERR	CR%	T(sec.)	MAX-it
POP=8	GRO	0.027372	0.030459	-0.00309	100%	0.107105	7
	ABC	0.015478	0.039269	-0.02379	100%	0.167347	100
	CSA	0.039957	0.042912	-0.00296	97.78%	0.156383	100
	PSO	0.154228	0.177085	-0.02286	84.44%	0.145807	100
POP=20	GRO	0.005354	0.01705	-0.0117	100%	1.093379	95
	ABC	0.047642	0.07349	-0.02585	95.56%	0.2549	100
	CSA	0.041691	0.109692	-0.068	96.44%	0.233736	100
	PSO	0.023798	0.021396	0.002402	100%	0.146368	76

Table 5. Network algorithms performance (experiment 4)

	ALG.	MSE-TR	MSE-TS	MSE-ERR	CR%	T(sec.)	MAX-it
LIM=10	GRO	0.019679	0.037678	-0.018	100%	0.18416	14
	ABC	0.704651	0.715262	-0.01061	33.78%	0.193584	100
	CSA	0.362427	0.350213	0.012214	61.33%	0.151075	100
	PSO	0.607278	0.667325	-0.06005	60.44%	0.122344	100
LIM=20	GRO	0.014666	0.0154	-0.00073	100%	0.788708	57
	ABC	3.071112	3.144232	-0.07312	0%	0.223524	100
	CSA	1.881178	1.326047	0.555131	42.22%	0.195444	100
	PSO	4.64444	4.73333	-0.08889	0%	0.15077	100