Интенсивность конвекции жидкостей с разным числом Прандтля в вертикальном цилиндре большого удлинения

DOI:

На практике наиболее часто встречаются конвективные течения в цилиндрах небольшого удлинения (отношение высоты цилиндра к диаметру основания – l/d до 10) с различными граничными условиями [2; 3; 8; 12]. В предыдущих публикациях авторов [4; 5] содержатся результаты численного решения задачи о свободно-конвективном движении жидкости в цилиндре, в которых выполнено сопоставление полученных результатов с результатами опубликованных теоретических и экспериментальных исследований, проанализировано влияние удлинения (от 2 до 60) и градиента температуры на стенке цилиндра на интенсивность конвективного течения. Это модели- рование показало заметное конвективное движение в вертикальном цилиндре [4], которое не обладает осевой симметрией и качественно сходно с данными экспериментов [2; 3].

1. Постановка задачи

Исследуется свободно-конвективное движение жидкости в длинном вертикальном цилиндре (удлинения 60, 80, 100, 200). Движение смоделировано средствами CFD (вычислительная гидродинамика) в пакете Ansys CFX [6]. Предполагается:

– течение ламинарное;

– жидкость ньютоновская;

– изменение плотности от температуры использовано в приближении Буссинеска;

– задача стационарная.

Для рассматриваемой задачи уравнения неразрывности, количества движения и энергии имеют вид [1]:

div (б') = 0 ,

( U V ) U -^{X , >} + ^ At? + g e T ', ρ ₀    ρ ₀

UV T ' = xA T, где Т – температура; T0 – максимальное значение температуры; T´ = Т0 – T – отклонение температуры от T0; p0 = –ρ0gz + pref – гидростатическое давление (соответствующее механическому равновесию при постоянных температуре T0 и плотности ρ0); pref – минимальное давление в верхней точке цилиндра; p´ = p – p0 – отклонение от гидростатического давления; ρ0 – плотность d(ln p)

при Т _о; p = p₀ (1 - P Т ), в =      — коэффициент термического расширения; x — коэффициент

0       0                 at температуропроводности; и - скорость; V - оператор набла; ig - ускорение свободного падения; μ – коэффициент динамической вязкости.

Приняты следующие граничные условия (рис. 1):

– скорость на стенке равна нулю (условие прилипания на стенках);

– основания цилиндра теплоизолированы;

– на стенках поддерживается температура T_w ( z ) = T ₀ – γ z / l , γ = const; T ₀ = T_w (0) = T_h – температура стенки у нижнего основания цилиндра, а T_u = T_w ( l ) – температура стенки у верхнего основания;

– температура стенки не меняет своего значения в окружном направлении.

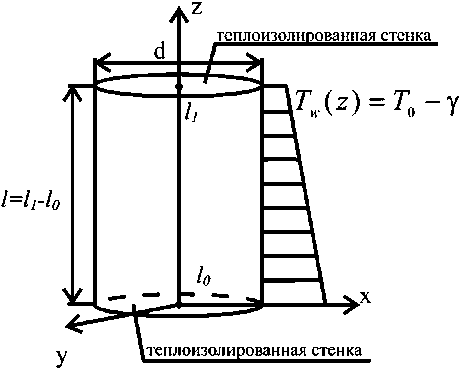
Рис. 1. Координаты и граничные условия

Цели и задачи заключаются в исследовании свойств свободно-конвективных течений в длинных вертикальных цилиндрах, выявлении характерных типов конвективного движения в зависимости от числа Рэлея.

2.    Верификация модели

Для проверки математической модели и подтверждения правильности получаемых результатов смоделирована конвекция воды в вертикальном цилиндре единичного удлинения ( h = 1). Граничные условия и геометрия заданы в соответствии с [1]. Ось симметрии цилиндра расположена вертикально. Температуры основания цилиндра Т_h и вершины цилиндра Т_u постоянны. Боковая поверхность теплоизолированная. T u = 295,15 К ; х = 1,415 - 10 - ³ см²/с; р = 997,3 кг/м³; ц = 0,9604 ^ 10 -3 Па ^ с, удельная теплоемкость при постоянном давлении с р = 4300,2 Дж/(клК); d = l.

Результаты расчетов, представленные в [1], имеют графический вид, поэтому приводится качественное сравнение. На рисунках 2–4 показаны сравнения распределения величин в различных сечениях, безразмерная температура вычисляется как T = ( T h - T )/( T h - T u ). Слева результаты, полученные Мюллером [1], справа – авторами статьи. Как видно, результаты очень схожи между собой. На рисунке 4 приводятся графики зависимости w = w /(// 1 ) от безразмерного радиуса в сечениях А и В. Видно хорошее согласование величин экстремумов скорости.

Проведенное сравнение дает основание полагать, что выбранный метод моделирования корректно отражает реальную картину процесса. Тем более что выбранные для сравнения результаты подтверждены экспериментально.

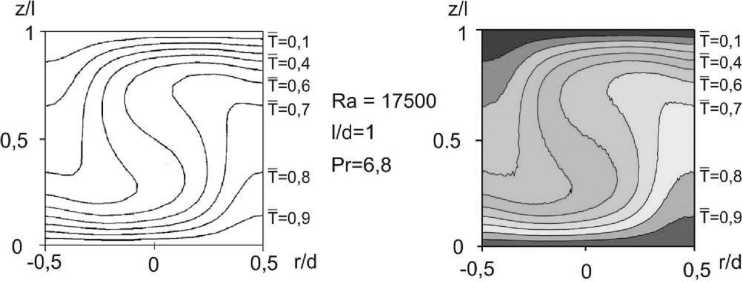
Рис. 2. Изотермы в вертикальной плоскости, проходящей через ось симметрии (температура относительная)

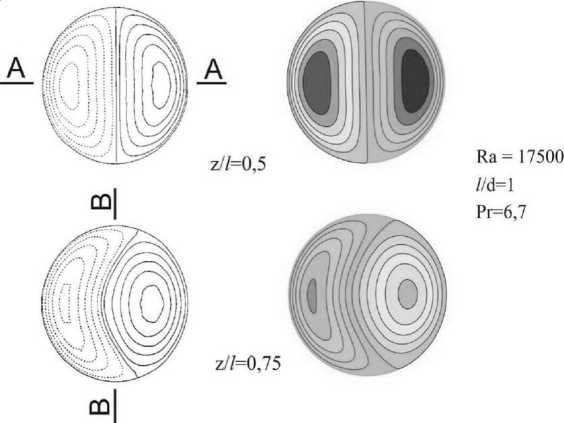
Рис. 3. Безразмерная вертикальная составляющая вектора скорости w = w /(// 1 ) в двух горизонтальных сечениях (на высоте z/l = 0,5 и z/l = 0,75)

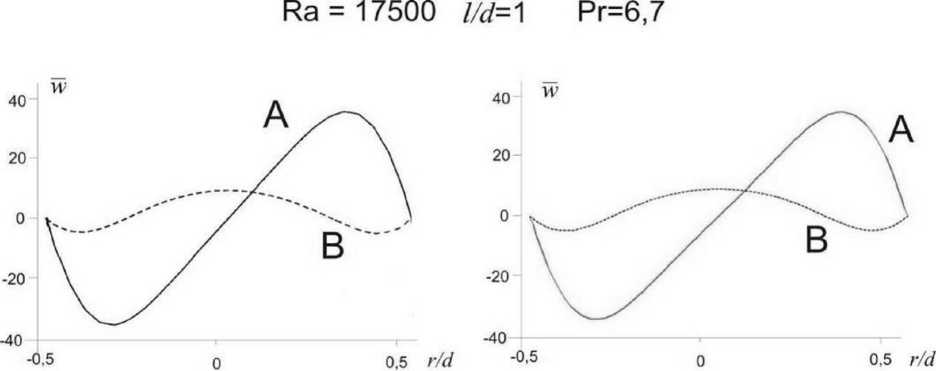
Рис. 4. Зависимость безразмерной вертикальной скорости w = w /(χ/ l ) от безразмерного радиуса в сечениях А и В (рис. 3) при z/l = 0,5 и z/l = 0,75 соответственно

3.    Численное моделирование конвективного течения в цилиндре

Основным безразмерным параметром конвективного движения является число Рэлея Ra = β gd ⁴ γ/ ν χ , здесь ν = µ / ρ – коэффициент кинематической вязкости; χ = λ / ρ c_p – коэффициент температуропроводности; λ – коэффициент теплопроводности. Число Прандтля вычисляется по формуле Pr = µ c_p / λ .

В работе [5] расчеты были выполнены для воды. В данной статье приводится сравнение результатов моделирования конвекции воды, пластовой нефти и дегазированной нефти. Свойства пластовых нефтей и условия моделирования представлены в таблице 1, свойства дегазированной нефти характеризуются усредненными параметрами: Pr = 4,5; с_р = 1 700 Дж/(кг ^• К); λ = 0,12 Вт/(м ^• К); µ = 0,32 мПа ^• с; ρ = 780 кг/м³; χ = 9,05 ^• 10^-8 м²/с; β = 8 ^• 10^-4 K^-1, числа Рэлея изменяется от 3 ^• 10³ до 7 ^• 10⁴.

На рисунке 5 представлены изовеллы вертикальной составляющей вектора скорости для разных жидкостей и градиентов температур. Видно, что для близких чисел Рэлея картины течения для различных жидкостей схожи.

Таблица 1

Основные параметры, определяющие свойства пластовых нефтей и конвективное движение

γ , K/м	0,013	0,011	0,012	0,01	0,021
ρ , кг/м3	640,1	679,8	680,3	700,8	773,3
с p , Дж/(кг • К)	1881	1855	1842	1851	1630
λ , Вт/(м • К)	0,096	0,101	0,102	0,102	0,133
µ , мПа • с	0,10	0,15	0,15	0,17	1,60
β , 1/К	0,00086	0,00101	0,00092	0,00111	0,00043
χ , м2/с	7,99 • 10-8	8,03 • 10-8	8,16 • 10-8	7,84 • 10-8	1,05 • 10-7
Ra	65707	56352	55487	51282	2940
Pr	1,955	2,749	2,703	3,094	19,626

Рис. 5. Поверхности равной вертикальной составляющей вектора скорости V _z цилиндра удлинением 100 (масштабы по вертикальной и горизонтальной оси не совпадают)

4.    Типы конвективного движения в цилиндре большого удлинения

На рисунках 6 и 7 представлены графики зависимости среднего по сечению значения моду ля вертикальной составляющей вектора скорости ^сред = —

- J Vdlxdy от безразмерной коорди-Sxy наты z/l для воды и дегазированной нефти при разных значениях чисел Рэлея. Отметим, во-первых, что отсутствуют принципиальные различия в зависимостях для воды и дегазированной нефти. Во-вторых, видно, что для чисел Рэлея от 4 039 до 12 116 при z/l от 0,2 до 0,8 скорость изменяется слабо. Средняя скорость Vz ссерчед не совсем постоянна, но амплитуда колебания А1/2 невелика по сравнению с максимальным значением. Для чисел Рэлея от 13 000 до 40 000 амплитуда А2/2 колебания значений Vz ссерчед намного выше. Это говорит о периодической смене интенсивности потока в вертикальном направлении.

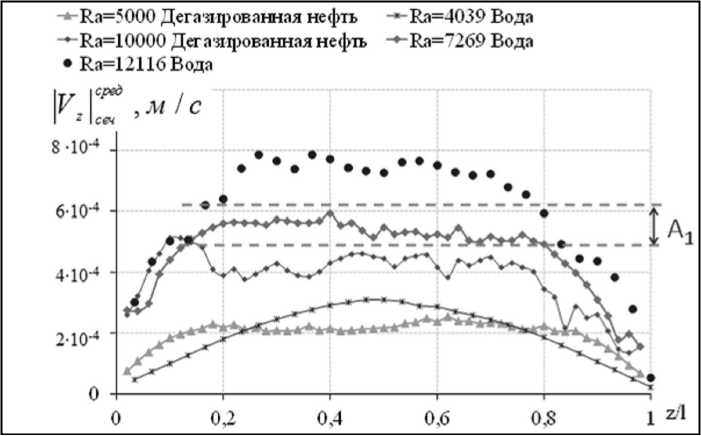
Рис. 6. Зависимость среднего по сечению значения модуля вертикальной составляющей вектора скорости

V _z ^с _се ^р _ч ^ед от относительной координаты цилиндра z / l «винтового» движения

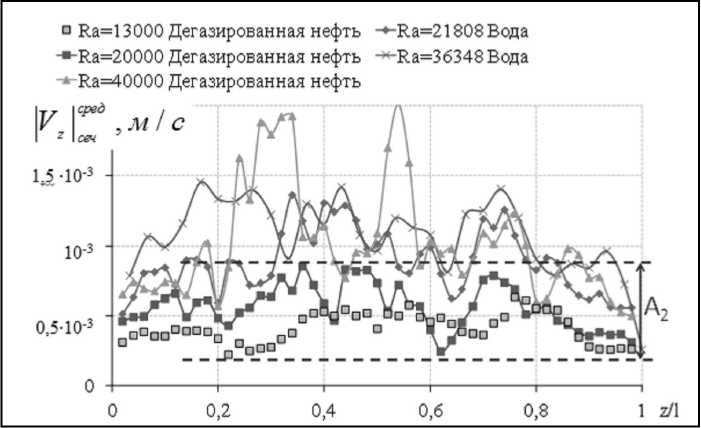
Рис. 7. Зависимость среднего по сечению значения модуля вертикальной составляющей вектора скорости

V _z ^с _се ^р _ч ^ед от относительной координаты цилиндра z / l «ячеистого» движения

Таким образом, для рассмотренных чисел Рэлея существует два типа конвективного движения – «винтовое» и «ячеистое», различие между которыми видно по амплитуде колебания средней по сечению вертикальной скорости (рис. 6–7) и по взаимному расположению восходящих и нисходящих потоков (рис. 8). Стрелками на рисунке 8 показано перемещение потока при увеличении высоты z / l .

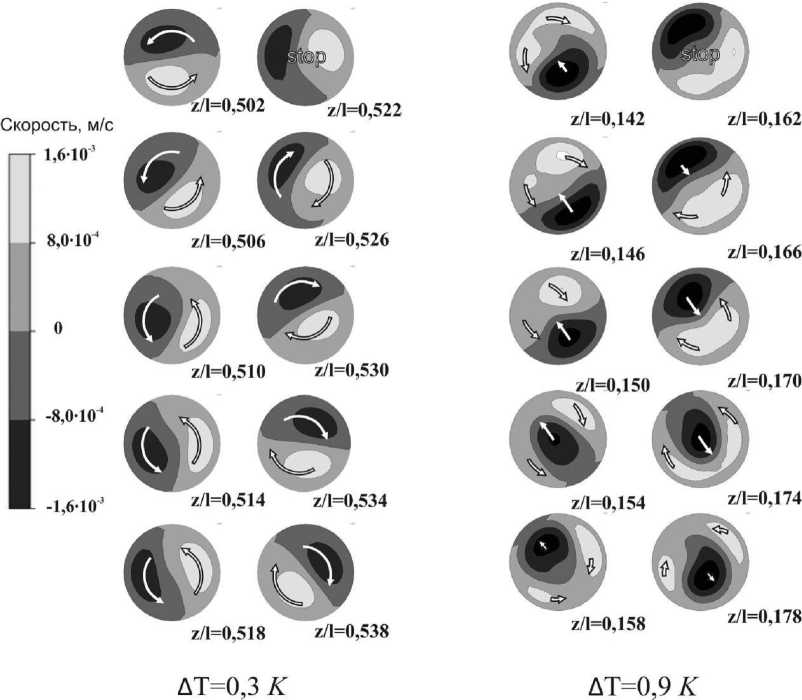
Рис. 8. Взаимное расположение восходящего и нисходящего потока в поперечном сечении цилиндра удлинением 100. Слева – «винтовое» движение, справа – «ячеистое»

Средняя вертикальная составляющая вектора скорости в срединной части цилиндра (от z/l = 0,2 до z/l = 0,8) вычисляется по формуле: Vz сорбед

5 0П_ТГ сред / Z ^ _

= - | V_z\_cm d I — I. Эта величина характеризу- ³ 0,2 сеч к ¹ )

ет интенсивность конвекции. При переходе к безразмерной скорости для получения универсаль- ной зависимости принят масштаб скорости [7]: ur =

f Q. к Pc p

■ g

Y J

где Q ₀ – среднее значение моду-

ля теплового потока через боковую стенку, которое вычислялось средствами постпроцессора

Ansys CFX. В этом случае V _z

сред об

сред z об ur

.

Как видно из рисунка 9, полученные в результате моделирования значения V _z ^сред хорошо

«ложатся» на одну кривую.

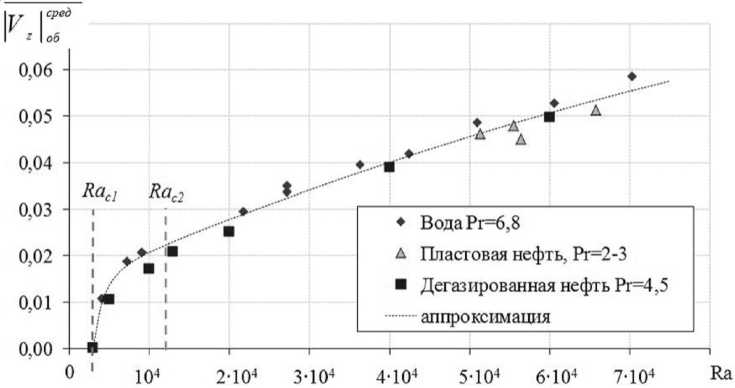
Рис. 9. Зависимость безразмерного среднего по о бъему значения модуля вертикальной составляющей вектора скорости V _z ^сред от числа Рэлея

Зависимость, представленная на рисунке 8, аппроксимирована формулой:

V сред = 0,012 + 7,73 • 10 - ⁷ Ra - 2,29 • 10 ^{- 12} Ra ² + ³⁴¹¹ - ^2,31 ' 10 . ^{z об}                                               Ra Ra ²

В расчетах при Ra_{с 1} = 3 100 фиксировалось начало «ячеистого» движения (что хорошо согласуется с результатами, полученными другими исследователями [1; 9; 11]). Переход от «винтового» движения к «ячеистому» проявляется при Ra_{с 2} = 12 000.

5.    Критерий бесконечности цилиндра

Для распространения полученных результатов расчетов на цилиндры бесконечного удлинения, необходимо определить такое удлинение, при котором дальнейшее его увеличение (при фиксированном Ra ) не ведет к изменению интенсивности конвекции и вида течения. Из таблицы 2 видно, что средняя по объему вертикальная скорость принимает одинаковое значение для удлинений, начиная с 60.

Таблица 2

Основные параметры конвективного течения воды в цилиндрах разного удлинения для двух чисел Рэлея

Ra	Удлинение
		30	60	80	100	200
9 087	V сред , м/с z об	3,9 • 10-4	5,9 • 10-4	5,9 • 10-4	5,9 • 10-4	5,9 • 10-4
27 261	сред V , м/с z об	0,7 • 10-3	1,1 • 10-3	1,1 • 10-3	1,1 • 10-3	1,1 • 10-3

Заключение

Изучено конвективное течение в цилиндре большого удлинения при постоянном градиенте температуры на боковой поверхности для чисел Рэлея от 3d03 до 7-104. Установлена зависимость интенсивности вертикального движения от числа Рэлея. Определено критическое число Рэлея начала конвективного движения. Найдена граница по числу Рэлея, при котором среднее значение по сечению модуля вертикальной составляющей скорости начинает испытывать значительные колебания с изменением высоты цилиндра, а также меняется форма течения. Предложена клас- сификация видов движений, а также масштаб скорости, позволяющий ввести единую для различных жидкостей зависимость безразмерной средней по объему вертикальной скорости движения от числа Рэлея. Установлен критерий «бесконечности» цилиндра.