Interacting spinor and electromagnetic fields in cosmology

In some earlier studies it was found that due to the presence of non-diagonal components of energymomentum tensor (EMT) the nonlinear spinor field in BI space-time automatically becomes massless and linear or leads to the isotropization of space-time [1], [2]. Whereas, in case pure electromagnetic field with induced nonlinearity there occurs severe restrictions on the components of vector potential. It was found that if the electromagnetic field is given by the 4-vector potential Дм = (0, 4, 4, 4), the corresponding non-diagonal components of EMT leads to 4 = 4 = 4 and space-time becomes isotropic [3]. The motivation for considering the interacting system was to see whether such generalization can remove the restrictions mentioned above.

• ¹    E-mail: bijan@jinr.ru

• 1.    Basic Equations and their solutions

The interacting system of material fields we choose in the form

L = 2 [們"▽力- ▽"們"封- …-人1"K)- 言耳"fТ"X(k),          ⑴ with X(К)三 1 + XzZ(К). Нere Ai is the self coupling constant, A2 is the coupling constant. In case of A2 = 0 we have spinor and electromagnetic fields those are minimally coupled to each other. Here У (К) and Z (К) are some arbitrary functions of invariant К generated from the real bilinear forms of the spinor field, such that К = {/, J, / + J, I - J}, / = S2 =(力3)2, J = P2 =(痴斤53)2• It can be shown that К = C2/V2 where C = const. This relation is liue for К = {I, J, I + J, I — J} for a. massless spinor field, whereas for К = I it is valid for massive spinor field as well.

The gravitational field is given by the metric ds2 = dt2 - 01而12 - 02面22 -嫉"办2,

⑵

where the metric functions 电 are the functions of t only. We also consider the case when the spinor and electromagnetic fields depend on time only, i.e., 3 = 3(t ), 3 = 3(t) and / 勿 = Ai (t), z = 1, 2, 3. On account of the non-diagonal components of the EMT in this case we find the following system of Einstein equations:

迈+逅+也州=/马 + q质a2-[2a2 - ^2a2]+虫吟q", @2   аз   а2 азX

⑶

⑷

⑸

⑹

⑺

⑻

⑼

逅 + 包 + ^ 包=/pi + Q [[2а2-[2a3 - [2a1] + 虫*"qQ ], аз   ai   аз aiX

包 + 必 + 包^ = jpi + q [[2a3-[2a1 -[2a2] + 4A『。(5 , ai    a?    ai a?          [X

包必 + «2 «3 + «3 包=呂[p2 + qQ], ai。2    。2。3

0 = 41 (> - ІІ 卜 3 + 2[i[2a2Q,

0 = 譽(a3 -巴)A2 + 2[3[iaiQ, 4a3 \@3ai /

0 = 产偿-^)工 +2[2[3a3Q.

4a2 \a2a3 /

As one sees, the foregoing system is overridden. But one can use a few of them as constraints to define, for example, initial values for metric functions ai and directional Hubble parameters 留. In the foregoing system we denote, Pi = Ai (У — 2КҮк ), P2 = ^spS + АіУ, Q = 1/(8 冗 V²X ), Q = [2ai + [2a2 + [2a3, Үк = df/dR and Z k = dZ/dК. Here A* = 3?57*3 is the pseudo-vector constructed from Dirac spinor and 仇 is integration constants: Ai = -a2[i/(VX) with V = ai@2@3 is the volume scale of BI- metric. Beside these, from the spinor field equations it is possible to show that

S² + p² + a ⁰²

c0

V2,

A1

ci V

A2

C2

V

A3

C3 V

where co, ci, C2, C3 are constants of integration. Introducing the directional Hubble parameters Hi we rewrite the Einstein equations (3) - (5) as follows:

a i	= H 1 a i.	(П)
a 2	= H2a2,	(12)
a 3	= H 3 a 3,	(13)
• Hi	—2 卜 i + Q 卜 a 3 + q2 a 2 3q1 a i +   X Q ]]
	- 2 [ 2H2 + HiH2 + H3Hi - H2H3 ] ,	(14)
' H2	=1 [「 i + Q [ q2a3 + q2a? - 3q2a2 ] + 込 g 迩 q ' 2 L                                  X
	- 2 [ 2H2 + HiH2 + H2H3 - H3Hi ] ,	(15)
' H3	=1 [「 i + Q [ q2a2 + q2a? - 3q2a2 ] + 込 g 迩 q ' 2 L                                  X
	- 2 [ 2H2 + H3Hi + H2H3 - HiH2 ] .	(16)

The remaining equations we exploit to find the initial values of metric functions and Hubble parameters. From the non-diagonal equations (7) - (9) we have cic2q1q2a1a2 + c2C3q2q3a2 @3 + сзс1дзд1аза1 = 0,

with the solution

C2 c3q2q3 a2 a3 ^a i —                    .                ,

CiC2qiq2a2 + C3Ciq3qia3 whereas from (6) we find

什 =K ( P2 + QQ ) - H2H3 ¹ -       H2 + H3      ■

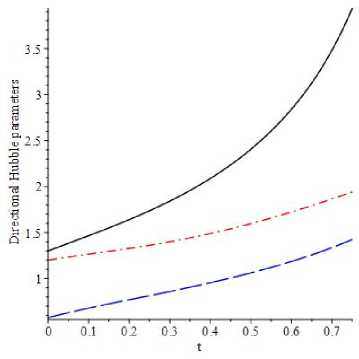
In what follows we solve the system (11) - (16) together with (18) and (19), numerically. The system, in question, is a multi-parametric one which can be exploited to find different types of solutions. For simplicity we choose c 勿 ： c i = C2 = C2 = 1 and qi = 0.2, q2 = 0.5, q3 = -0.03. Note that we should choose q 勿 and c 勿 as well as a2 ( 0) and 03(0) in such a way that (18) provides real value for ai(0). Further we choose the self-coupling constant Ai = 0.4 and the coup ling constant A2 = 0.5. We choose Z (К) = К ⁿ2 and set П2 = 2. Note that П2 can be chosen both positive and negative. The initial values for the metric functions and Hubble parameters we set a2 ( 0) = 1.2, a3 ( 0) = 1.3, 次( 0) = 1.2 and %(0) = 1.3. For these values of problem parameters from (18) and (19) we find ai(0) = 0.439 and %(0) = 0.574, respectively. The spinor field nonlinearity we choose in the form [4,5]

У (К) = (g + Ai К ^(1+tt) / ²)^{1/ ( 1+tt}) , В > 0,   0 < a < 1,                      (20)

that describes a Chapligin gas. Here we choose В = 1 and a = 0.5. The corresponding solutions are given in Fig. 1. In Fig. 1 we plot the metric functions and Hubble parameters, respectively. In the figures blue long dash line, red dash dot line and black solid line stand for t, g and г-component of metric function and Hubble parameter, respectively. Note that the spinor field nonlinearity can simulate different types of sources including perfect fluid, quintessence, cosmological constant, phantom matter, Chaplygin gas, modified quintessence, modified Chaplygin gas, quintom matter etc. So exploiting this property of spinor field nonlinearity one can find different types of solutions.

Conclusion

Within the scope of BI cosmological model we have studied the interacting system of spinor and electromagnetic fields. The corresponding field equations are derived and solved numerically. Some severe restrictions, occurred in case of pure spinor or electromagnetic fields, were removed.

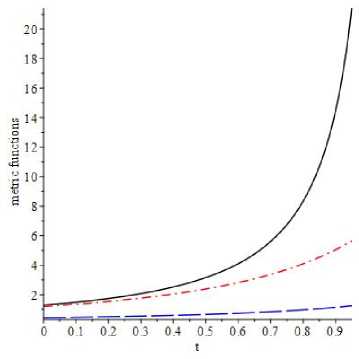
Fig. 1. a) Evolution of the metric functions ai (blue long dash line), 。 2 (red dash dot line) and 03 (black solid line), when the spinor field nonlinearity describes a Chaplygin gas. and b)Evolution of the directional Hubble parameters Hi (blue long dash line). H2 (red dash do 〔 line) and H3 black solid line.

b

Acknowledgment: This paper has been supported by the RUDN University Strategic Academic Leadership Program.

Dedication: I would like to dedicate this report to the blessed memory of one of the best cosmologists of our time, Professor A.A. Starobinsky. Since 2007, when I first attended a conference organized by the Russian Gravitational Society, we have met several times at conferences. Whenever I asked his opinion about my work, he gave valuable advice. Although in earlier years he was very skeptical about using the spinor field in a classical manner, he eventually said that such an approach has a right to exist. I will definitely miss him at upcoming conferences.