Интерфейс для моделирования эластик Эйлера в программной среде Mathematica

Задача Эйлера об эластиках имеет следующую геометрическую формулировку. Даны две точки й = (т ^ , у ^ ) Е R 2 , г Е { 0, 1 } , с закрепленными в них единичными векторами « ^ Е Т _а . R 2 , | « ^ | = 1,г Е { 0,1 } . Требуется найти гладкую кривую 7(t) фиксированной длины Z, выходящую из точки й о с вектором скорости « о и попадающую в точку й 1 с вектором скорости « 1 (см. рис. 1) . Кроме того, на кривую накладывается дополнительное условие — интеграл квадрата кривизны имеет наименьшее значение вдоль искомой кривой:

/ " 1 k ² (t) 0

dt ^ min.

Задача имеет простой физический смысл: дан упругий стержень фиксированной длины с закрепленными концами и направлениями стержня в концах. Требуется определить форму стержня. Возможные формы, которые может принимать упругий стержень, открыл Эйлер [1] , они называются эйлеровыми эластиками.

Работа поддержана Российским фондом функдаментальных исследований, проект 12-01-00913-а.

○ c А. А. Ардентов, 2012

○ c Программные системы: теория и приложения, 2012

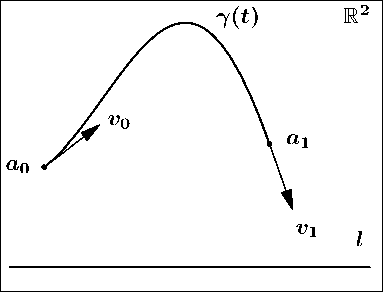
Рис. 1. Геометрическая постановка задачи

Первая параметризация эластик эллиптическими функциями была получена Л. Заалшютцем [2] . Вопрос об оптимальности эластик был поднят в диссертации Макса Борна [3] : будущий нобелевский лауреат доказал отсутствие сопряженных точек на эластиках без точек перегиба, т. е. что все неинфлексионные эластики являются локально оптимальными. Ю. Л. Сачков получил оценки точек разреза [4] , в которых эластики теряют глобальную оптимальность, и сопряженных точек [5] , в которых теряется локальная оптимальность. Различные вопросы, связанные с оптимальностью эластик, рассматривались в работах [6 –10] .

В данной работе представлены формулы для вычисления эластик, а также описание демонстрации в среде Mathematica [11] , с помощью которой можно через web-интерфейс построить эластику любого типа и формы, а также получить параметризацию эластики.

• 2.    Экстремальные траектории в задаче оптимального управления

Так как | v t | = 1, то далее рассматриваются вместо векторов соответствующие углы 9 _t такие, что v t = (cos 9 _t , sin 9 _t ) Без ограничения общности начальная точка может быть выбрана в начале координат ((х ₀ ,у ₀ ) = (0, 0)), а начальный угол 9 0 установлен равным 0 (т. е. касательная параллельна оси От). Этого можно достичь за счет выбора системы координат на плоскости R ² .

Описанная задача может быть также сформулирована как задача оптимального управления [12] в пространстве М = R ²^ х S g

следующим образом:

(х \    / cos 9 \ у = sin 9   + к 0   , к Е R,

9 /  \ 0 /

( 0 \                   / х₁ \

0 I ,       q ^(t 1 ) = q i = I y i I ,

0 /\ 9i

K 2 ^(t)

dt ^ min.

Заметим, что кривизна кривой k(t) = ^X ² (t) + y ² (t) = | 9(t) | = | u(t) | .

Напомним основные результаты работы [13] . К рассматриваемой задаче оптимального управления был применен принцип максимума Понтрягина [14] . Полученная гамильтонова система для нормальных экстремалей сведена к уравнению математического маятника:

3 = c, c = — Sin 3,

где 3 — угол отклонения от устойчивого положения равновесия маятника, а c — его линейная скорость.

Таким образом, экстремальные траектории задачи параметризуются точками фазового цилиндра маятника, задающего пространство сопряженных переменных С = R _c х S ^ . Уравнение маятника (1) имеет следующий интеграл энергии:

Е = —— cos 3 Е [ — 1, + то ).

Для различных уровней энергии маятника получены разные выражения для экстремальных траекторий q(t) (см. [13] ). Отсюда получена классификация эластик, см. рис. 2 .

Более подробное описание каждого типа приведено в дальнейших пунктах 2.1, 2.2 .

• 2.1.    Невырожденные эластики

На рис. 3 показаны два основных семейства невырожденных эластик, выходящих из начала координат с нулевым начальным углом. Каждая траектория задается тройкой Ь о , к, г — эллиптическими координатами в пространстве сопряженных переменных [15] . На рис. 3

Эластики Эйлера

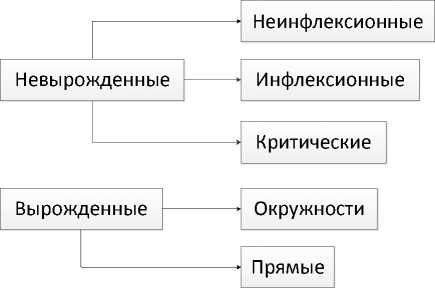
Рис. 2. Классификация эластик

траектории имеют конечную длину, которую задает параметр времени t.

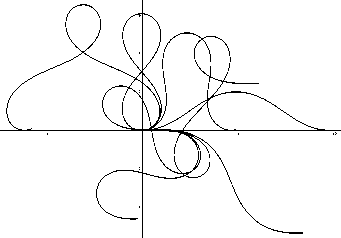
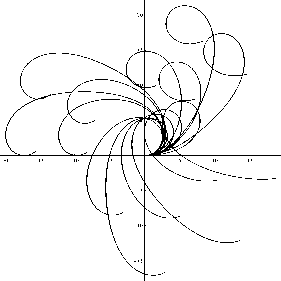
Рис. 3. Неинфлексионные и неинфлексионные эластики

Эллиптические функции Якоби, используемые в формулах, определяются следующим образом [16] :

ф = am u

⇔

*

u = F(-) = /

dt

V1 - к"² sin ² t ’

E(u) =

/* V"1 0

— к ² sin ² 1 dt,

sn u = sin am u, cn u = cos am u, dn u = V1 — к2 sn2 u, K(k) = F ( — ) .

Инфлексионными называют эластики, которые имеют на луче t e [0, + то ) бесконечное количество точек перегиба (см. слева рис. 3) . Уравнения этих кривых получены в работе [13] :

zMr, t) = t(2k ² sn ² b ₀ — 1) — 2 ((2к ² sn ² b ₀ — 1)( E(b _t ) — E(b ₀ )) +

+ 2к ² dn b ₀ sn b ₀ (cn b _t — cn b ₀)) ,

y(b ₀ , к, r, t) = 2кt dn b ₀ sn b ₀-- ^2k dn b ₀ sn b ₀ (E(b _t ) — E(b ₀ )) —

• —    к(2к ² sn ² b ₀ — 1)(cn b _t — cn b ₀)^ ,

где b _t = b ₀ + rt, b ₀ e R , к e (0,1), r e R ⁺ .

Рис. 4. Пример критической эластики

Неинфлексионными называются невырожденные эластики, которые на луче t e [0, +то) не имеют точек перегиба (см. справа рис. 3). Уравнения для этих кривых, как и для инфлексионных, зависят от времени t и параметров o,, к, г — эллиптических координат в пространстве сопряженных переменных [15]:

x(b o .к.г.t)

• -    Г^ Т sn T ( dn T - dn T ) + ( E ⁽ T ⁾ - кг l к к\ к к) у \ к /

  - E(к))Нк - 1))+( 1 - #s-- 2 к - i)t, ^{y(6 o} .^,•■.’'.ⁱ⁾ = - кг (^2cn к^sn к (^E (к) - ^E (к)) - (^dn к -

• -    dn bo Visn к - 1)) +2t( 1 - 1) cn bo sn bo.

к у у к у / у к2 / к к где bt = bo + rt, bo G R, к G (0. 1), г G R+.

Критические эластики представляют собой предельный случай инфлексионных и неинфлексионных эластик при к ^ 1 (см. рис. 4) . Их уравнения зависят от параметров b o , г, t:

x(b _o . г. t) = sh ² b _o (sh ² b _o - 1)t-- ^o (1(sh b _t - sh b _o ) th b _o +

+ sh b _o (sh ² b _o - 1)(th b _t - th b _o)^ .

y(b _o . г. t) = 2t sh b _o sh b _o ^o (1th b o (th b _t - th b _o ) - г

• -    sh b _o (sh b _t - sh b _o )(sh ² b _o - 1)) .

• 2.2.    Вырожденые эластики

где b _t = b _o + гt, b _o G R , г G R ⁺ .

К вырожденным эластикам относят окружности:

x(R. t) = R sin -I". R

y(R.t) = R (1

cos — ) , R .

где R — радиус окружности.

И наконец, прямые соответствуют самому простому и оптимальному случаю — стержень не деформирован, интеграл энергии равен 0, траектории глобально оптимальны до бесконечности:

x(t) = t.      y(t) = 0.

• 3.    Интерфейс в среде Mathematica

Для более наглядного представления траекторий введем для каждого типа эластики более естественные параметры, которые используются в интерфейсе для эластик (см. рис. 5) .

parameters of elastica angle0

k0.799

r 1

phase1

periods1

Out[6]=

graphic options type of elastica:     Inflectional Non-inflectional Critical Circle Line

Рис. 5. Интерфейс в свернутом виде

• 3.1.    Естественные параметры для эластик

Инфлексионные и неинфлексионные эластики являются наиболее общими типами эластик, которые параметризуются одинаковым вектором параметров (b o ,r, k,t).

Введем новый параметр Phase, который задает фазу эластики. Этот параметр соответствует параметру b o , отсюда формулы перехода: Phase = am ^ 0 ,b o = г F(Phase) .

Окружности, инфлексионные и неинфлексионные эластики являются периодическими. Введем параметр Periods = ^ , где Т — период эластики. Выражение периода эластики зависит от типа эластики:

∙

для инфлексионной эластики Т =

∙

∙

для неинфлексионной Т = для окружности Т = 2~R.

2 к K(k) .

Г ;

4K(fc) .

г ;

Для критических и прямолинейных эластик далее вместо параметра времени t будем использовать параметр длины Length = t.

• 3.2.    Функции интерфейса

В среде Mathematica запрограммированы 5 модульных функций вычисления эластик по параметрам, которые описаны в подразделе 3.1. Для вычисления различных типов эластик использовались соответствующие формулы, описанные в подразделах 2.1 , 2.2. На рис. 6 приведена одна из новых схем быстрого вычисления формул, задающих невырожденные эластики, разработанная при создании интерфейса.

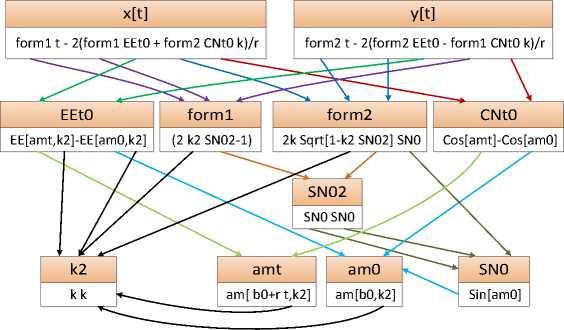
Рис. 6. Схема вычисления функций, задающих инфлек-сионную эластику

Головной модуль выполняет функции интерфейса. Основными элементами управления в интерфейсе являются ползунки (см. рис. 7) . Например, с помощью ползунка Angle задается начальный угол поворота эластики 9 о е [0, 2тт] (определенный в начале раздела 2) . Если нажать справа от ползунка на кнопку + , то появится меню для управления ползунком:

Ф Wolfram Demonstrations Project

TOPICS LATEST ABOUT

Paxametrization

x[t_] := 0.39714789063478056.(0.4130687614720834.t - 0.56981

y[t_] := 0.9177546256839811.(0.4130687614720834.1 - 0.569801

Рис. 7. Интерфейс на сайте

∙ В первом поле можно задать произвольное значение параметра в числовом (например, 124.7883 ), а также в символьном виде с помощью кода Mathematica (например, (Pi + Sin[1])/5!, для более подробной информации см. [11] ).

∙ Step Backward смещает ползунок на некоторую величину влево и соответственно увеличивает значение выбранного параметра, если оно не является максимальным.

∙ Play запускает анимацию с изменением текущего параметра.

∙ Step Forward смещает ползунок на некоторую величину вправо и соответственно уменьшает значение выбранного параметра, если оно не является минимальным.

∙ Faster увеличивает скорость выполнения анимации.

∙ Slower замедляет скорость выполнения анимации.

∙ Forward or Backward меняет закон, задающий направление движения ползунка: Forward — ползунок двигается только вперед, в конце переходя на начало; Backward — ползунок двигается только назад, переходя из начала в конец; Forward and Backward — ползунок двигается вперед-назад, меняя направление в конце и в начале.

Описанным меню обладают все ползунки интерфейса.

Поле Type of elastica может принимать 5 значений:

• (1)    Inflectional задает инфлексионную эластику (см. подраздел 2.1) ;

• (2)    Non-inflectional вычисляет неинфлексионную эластику (см. подраздел 2.1) ;

• (3)    Critical соответствует критической эластике (см. подраздел 2.1) ;

• (4)    Circle отображает окружность (см. подраздел 2.2) ;

• (5)    Line отображает прямые (см. подраздел 2.2) .

Каждому типу эластик соответствуют свои параметры (см. рис. 7 , блок parameters of elastica ):

• (1)    Angle, к, г, Phase, Periods для инфлексионных эластик;

• (2)    Angle, к, г, Phase, Periods для неинфлексионных эластик;

• (3)    Angle, г, b ₀ , Length для критических;

• (4)    Angle, Radins, Periods для окружностей;

• (5)    Angle, Length для прямых.

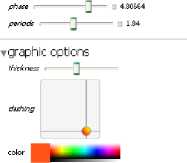
После основных параметров располагаются графические опции (блок graphic options на рис. 7) , общий для каждого типа эластики:

• ∙    thickness — параметр, задающий толщину линии;

• ∙    dashing задает пунктирный стиль кривой;

• ∙    color отвечает за цвет.

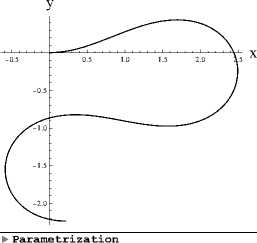
• 4.    Заключение

По заданным параметрам интерфейс выдает изображение дуги эластики длиной t и запись на языке Mathematica функций, задающих параметризацию (блок Parametrization на рис. 7). У пользователя интерфейса есть возможность скопировать построенные в векторном формате линии в буфер обмена. Для этого достаточно два раза нажать правой кнопкой мыши на кривую, после чего кривая и рамка вокруг нее выделится оранжевым цветом. Далее стандартным сочетанием клавиш скопировать выделенный объект в буфер, а затем вставить его в произвольный документ, поддерживающий взаимодействие с векторной графикой (например, в документ Microsoft Word).

Для автозапуска анимации текущего типа эластик следует нажать на внутреннюю кнопку Autorun в правом верхнем углу интерфейса. В результате возникнет дополнительное меню Autorun , имеющее те же кнопки, что и расширенное меню ползунка.

Описанный в статье интерфейс размещен на сайте Wolfram [17] .

Интерфейс имеет формат вычисляемого документа (CDF), который ставит в центр легкую в создании интерактивность, предоставляя пользователям возможность управлять содержимым и генерировать результаты в режиме реального времени.

Для работы интерфейса необходимо лишь скачать и установить бесплатный CDF-Player (свободен для скачивания в интернете по адресу . Этот плеер позволяет смотреть через интернет приложения Wolfram Demonstration Project, не устанавливая систему Wolfram Mathematica.

Представленный интерфейс является примером использования программных средств Wolfram Mathematica для решения актуальной задачи теории упругости, теории управления и компьютерной графики. Он может использоваться исследователями, а также преподавателями, аспирантами и студентами при изучении данных областей.