Интерференционное управление поглощательной способностью магнитной пленки

чения поля ферромагнитного резонанса (ФМР) на заранее установленной частоте. Существенно, что, изменяя начальную разность фаз падающих встречных волн при заданном значении внешнего поля, можно добиться существенной вариации величины поглощения в максимально возможных пределах – от бездиссипативного переноса энергии через слой до практически полного поглощения.

1.    Материальные соотношения

Рассмотрим плоскопараллельный слой (пленку), ограниченный плоскостями y = 0 и y = d и намагниченный в своей плоскости до насыщения постоянным внешним магнитным полем H , направленным вдоль оси OZ . При этом ориентации векторов намагниченности M и поля H совпадают. В случае нормального падения ли-нейнополяризованной электромагнитной волны на пленку внутри нее возможно распространение двух собственных волн с компонентами поля H_x , H_y , E_z (ТЕ-волна) и E_x , E_y , H_z (ТМ-волна). Далее будем рассматривать только одну из этих волн – ТЕ, так как она является управляемой внешним магнитным полем. Ее волновые характеристики определяются комплексным показателем преломления:

N (ω) = n - i κ = ε(ω)µ _⊥ (ω) ,                     (1)

где ε(ω) = ε - i 4πσ ω – комплексная диэлектрическая проницаемость, мнимая часть которой на частоте ω пропорциональна удельной проводи © А.С. Абрамов, С.А. Афанасьев, Д.И. Семенцов, 2013

мости ст. Эффективная магнитная проницаемость слоя для заданной ориентации подмагничивающего и волновых полей может быть представле- на в виде [9]:

- 1 (to) = --- a -

(to н + to м ^{)2 -} (ю - i £ю н ⁾²   (2)

^to н ^(to н ^{+ to} м ) -^{(to -} i ^^to н ) 2

где - и ± i - a — диагональные и недиагональные компоненты тензора магнитной проницаемости; toм = 4луM; toн = ун; у = 1.76 ■ 107 (Э ■ с)-1; ^ - параметр релаксации. При указанной геометрии задачи максимум эффективной проницаемости -^(to) определяет резонансную частоту tor = ^]toн (toн + toм) (при фиксированном значении подмагничивающего поля) или резонансное значение поля нг = 2пM(Д1 + (to/2луM)2 -1) (при фиксированном значении частоты). При этом па- раметр релаксации связан с шириной резонансной кривой соотношением ^ = Ан / нг.

• 2.    Энергетические соотношения для встречных волн

Рассмотрим теперь случай нормального падения из вакуума на слой магнетика двух встречных когерентных волн. Считая временную зависимость всех волновых полей пропорциональной фактору exp( i to t ), координатную зависимость для падающих на слой встречных волн запишем в виде:

нАх = A exP[i(фA - k0 У)] , EAz = нАх , нВх = B exp[i(ФB + k0 У)] , EBz = -нВх .

Здесь A и B — амплитуды встречных волн; ф A и ф в — начальные фазы; k o = to/ c , c — скорость света в вакууме. Решение граничной задачи с учетом необходимых граничных условий для волновых полей приводит к следующим выражениям для суперпозиции электрического и магнитного полей отраженных и прошедших волн: в области у < 0

н ^х = F exp[ i (ф A + k o у )],    Efz = - ^x      (4)

и в области у >  d

H Gx = G exp[ i (ф в - k o У )], Egz = H Gx .      (5)

Здесь введены комплексные амплитуды F = = Ar A + Bt B и G = At A + Вг в , а также амплитудные коэффициенты отражения и пропускания:

r A = iC( Z ² - 1)sin kd = | r A | exp( i x A ),

Г в = r A exp(2 ik o d ) = r A I exp( i X в ),              (6)

tA, в = 2 ZC exp( ikod) = |tA, b| exp( i V A, в), где

C = [2 Z cos kd + i ( Z ² +1) sin kd f¹;

Z = (-_±/s)¹² — волновое сопротивление и k = = k o N (to) — волновое число в магнетике. Коэффициенты (6) являются известными амплитудными коэффициентами отражения и пропускания тонкого слоя одиночной волны [10].

Потоки энергии падающих волн запишутся в виде ^ o1 = ( c / 8л) A ² и ^ o3 = ( c / 8л) B ². Потоки энергии, уходящие от поверхностей слоя в областях у < o и у >  d , могут быть представлены в виде суммы трех слагаемых:

5 1 = S 1 A + S B + S 1 ^nt = ( c / 8л)[ R A A ² + T B B ² +

+ IAB cos(5-y в +X A )],                      (7)

S 2 = S A + S 2 + S 2 ^nt = ( c / 8n)[ T A A ² + RbB ² + + IAB c^os(5 + v A ^- x в )].

Здесь введены энергетические коэффициенты отражения и прохождения для одиночных волн R A B =1 r A B 1 2 и Tab =| t A в |², а также параметр I = 2Д rA |² t B |² — коэффициент интерференционной прозрачности. Слагаемые, включающие этот коэффициент, обеспечивают интерференционное перераспределение энергии между отраженными от слоя и прошедшими через него потоками. Величины x A в и v A в — сдвиги фаз, приобретаемые волнами при отражении и прохождении через слой, 5 = ф в - ф A + k o d — разность фаз падающих волн, где ф в - ф A — разность фаз падающих на соответствующие границы волн, d – толщина слоя.

Поглощательную способность магнитного слоя определим отношением поглощаемой им мощности к суммарной мощности падающих волн. В режиме распространения встречных волн выражение для коэффициента поглощения принимает следующий вид:

D = D o ^- D int ^(A,⁵⁾,

D_o = 1 - R - T ,

2 IAB

D int (А, 5) = —----_ч cos(V A - X в ) cos 5.

A ² + B в^

• 3.    Численный анализ

Ниже приведены результаты численного анализа отражательной, пропускательной и поглощательной способности тонкой магнитной пленки (выращенной из монокристаллической феррошпинели MnFe₂O₄), полученные в широком диапазоне толщин d и начальных разностей фаз 5 для различных соотношений амплитуд прямой «сигнальной» волны и встречной волны «подсвет-

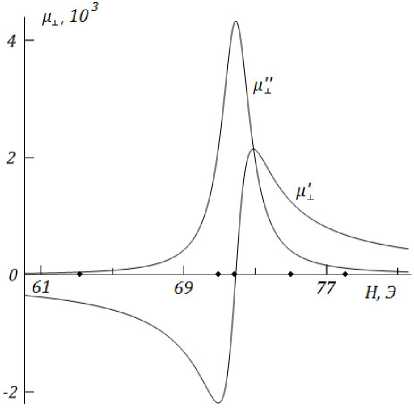
Рис. 1. Полевые зависимости действительной и мнимой частей магнитной проницаемости монокристаллической феррошпинели

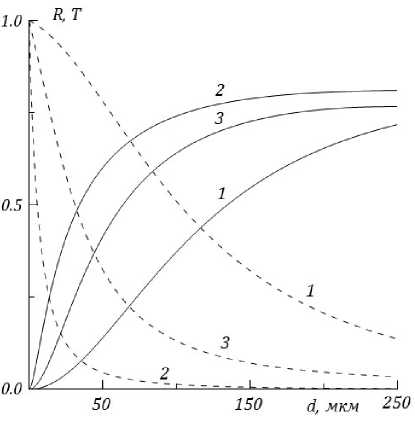
Рис. 2. Зависимости коэффициентов отражения и прохождения (сплошные и штриховые кривые) одиночной волны от толщины слоя, H = 63.3, 72, 75 Э (кривые 1-3)

ки». Для численного анализа использовались следующие параметры указанного магнетика: вещественная часть диэлектрической проницаемости б = 10, удельная статическая проводимость ст = 0.64 ■ 10¹⁰ c 1 , намагниченность насыщения 4п M о = 4400 Гс, значение резонансного поля H r = 72 Э, ширина линии ФМР A H = 4 Э. При заданных значениях ширины линии ФМР и резонансного поля значение параметра релаксации § = A H/H r = 0.055 [11; 12].

На рис. 1 приведены зависимости действительной ц' и мнимой ц" частей магнитной проницаемости от приложенного внешнего магнитного поля H , построенные на рабочей частоте f = _ю/2п = 10¹⁰ Гц. На оси абсцисс точками отмечены значения поля H = (63.3, 71, 72, 75, 78) Э, которые далее будут использоваться при численном анализе. Значениям поля H = 63.3 Э и H = 78 Э отвечают малые магнитные потери, значениям H = 71 Э и H = 72 Э — большие потери. При H = 72 Э выполняется условие n' — n ", т. е. приближение хорошо проводящей среды, поле H = 75 Э отвечает переходной ситуации между слабым и сильным поглощением. Величина ц" при резонансном значении поля H_r достигает значения ц" — 4333. Видно, что наиболее эффективное управление магнитной проницаемостью пленки и, следовательно, ее поглощательной способностью возможно в диапазоне подмагничивающих полей H — 68...76 Э .

Вначале рассмотрим ситуацию нормального падения на магнитный слой только одной «сигнальной» волны, падающей из области у < 0 (или из области у > 0). На рис. 2 проиллюстриро- ваны зависимости коэффициентов отражения R и T (сплошные и штриховые линии) от толщины слоя d, соответствующие значениям внешнего магнитного поля H = (63.3, 72, 75) Э, т. е. трем различным уровням поглощения. Кривые 2 отвечают резонансному полю Hr, при котором феррошпинель лучше отражает и хуже пропускает падающее излучение, т. е. ведет себя как типичный металл. При малом смещении поля от резонансного поведение коэффициентов изменяется – за счет уменьшения отражения несколько возрастают прохождение и поглощение. Наконец, при достаточно большом удалении от резонанса имеет место слабое поглощение (кривые 1). В этой области пленка феррошпинели подобна диэлектрику с потерями.

Перейдем теперь к рассмотрению случая нормального падения «сигнальной» волны с амплитудой A и встречной по отношению к ней волны «подсветки» c амплитудой B = 0.15 A . На рис. 3 приведены зависимости коэффициента интерференционной прозрачности слоя феррошпинели от его толщины, полученные для указанных на рис. 1 значений магнитного поля (кривые 1–5). Кривые 1 и 5 отвечают слабому поглощению, 2 и 3 сильному, кривая 4 соответствует переходной области между слабым и сильным поглощением. Видно, что наиболее эффективное управление прозрачностью слоя возможно вдали от области резонанса. Здесь достигается максимальное значение коэффициента интерференционной прозрачности I (кривая 1). Тем не менее прозрачностью слоя можно управлять, хотя и в меньшей степени, даже при резонансном значении поля.

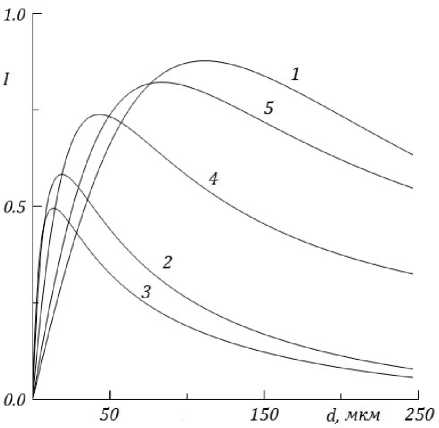
Рис. 3. Зависимость коэффициента интерференционной прозрачности от толщины слоя для двух встречных волн при 8 = 0, H = 63.3, 71, 72, 75, 78 Э (кривые 1—5)

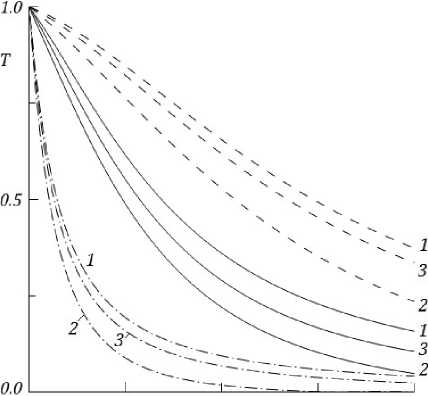
25        50        75 d, мкм

Рис. 4. Зависимость коэффициента усиления от толщины слоя, при 8 = 0, п/2, п (кривые 1—3) и H = 72,75,78 Э (штрих-пунктирые, сплошные, штриховые кривые)

Рассмотрим теперь эффект «просветления» магнитного слоя по отношению к «сигнальной» волне. Покажем, что встречная волна «подсветки» обеспечивает усиление «сигнальной» волны по сравнению со случаем ее прохождения через слой магнетика, когда она является одиночной. Усиление сигнала будем характеризовать коэффициентом преобразования [3]:

к = S 2 / S 01 = T + I ( B / A )cos(8 + V a -X в ), (9) который характеризует изменение интенсивности сигнала при его прохождении через слой магнетика. Управляя амплитудами и фазами встречных волн, можно добиться как усиления прошедшего сигнала, так и его ослабления. Отметим, что увеличение интенсивности проходящей волны достигается не за счет добавления к ней отраженной от второй границы волны «подсветки», а за счет интерференционной перекачки энергии между волнами внутри слоя. При определенном подборе амплитудно-фазовых характеристик возможен даже идеальный случай, когда вся падающая на слой энергия уходит от слоя в направлении прошедшей «сигнальной» волны.

На рис. 4 приведены зависимости коэффициента преобразования K «сигнальной» волны от толщины слоя d, полученные для трех значений внешнего поля H = (72, 75, 78) Э (штрих-пунктирые, сплошные, штриховые кривые) и разностей фаз 8 = 0, п/2, п (кривые 1—3). Видна возможность эффективного управления пропус-кательной способностью слоя за счет изменения подмагничивающего поля и разности фаз пада- ющих на слой волн. Так, при H = 75 Э значение коэффициента K в слое толщиной d = 100 мкм может варьироваться от 0.05 до 0.17 (тогда как в отсутствие волны «подсветки» K — 0.12). При поле H = 78 Э значение K находится в диапазоне (0.17…0.3). Для сравнения, диапазон значений K при резонансном значении поля составляет лишь (0.01…0.05).

Выражение (9) определяет коэффициент прохождения одиночной волны при условии 8 = п/2 - (у а - X в ), где разность фазовых сдвигов V а - X в зависит как от толщины слоя d , так и от величины приложенного поля H . Для приведенных выше трех значений поля H такие разности фаз должны быть равны 8 = п/28, 2п/5 и 9п/20 соответственно. Таким образом, за счет наличия ИВВ появляется возможность как уменьшать, так и увеличивать прошедшую интенсивность «сигнальной» волны, т. е. возможны два взаимно обратных эффекта – «затемнения» и «просветления». Чем ближе значение внешнего поля к его резонансному значению, т. е. к области сильного поглощения, тем в меньшей степени описанные эффекты будут проявляться.

На рис. 5 представлены зависимости коэффициента поглощения D от толщины слоя в режиме одиночных ( а ) и встречных волн ( б ), полученные для разности фаз 8 = 0 (что соответствует максимальному значению D ). При распространении одиночной волны через слой величина коэффициента поглощения в пике не превышает значения D = 0.5, которое соответствует резонансному значению поля H r = 72 Э и толщине слоя d — 15 мкм. С ростом толщины слоя наблюдается

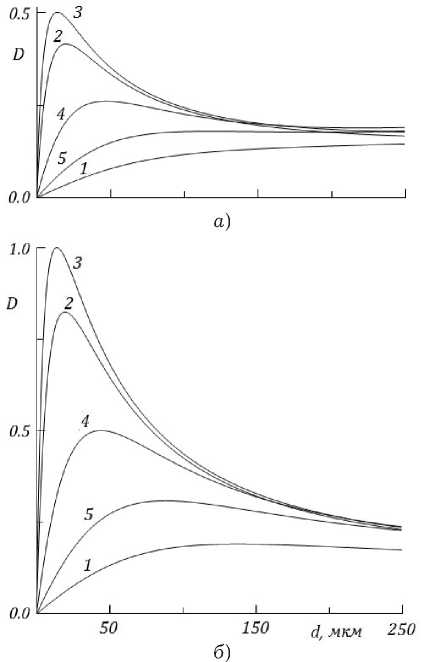
Рис. 5. Зависимость коэффициента поглощения от толщины слоя одиночной ( а ) и встречных ( б ) волн при 8 = 0 и H = 63.3, 71, 72, 75, 78 Э (кривые 1-5)

уменьшение коэффициента D , сопровождаемое либо слабо выраженными осцилляциями, либо выходом на насыщение. В режиме встречных волн величина коэффициента поглощения при резонансном значении поля может достигать значения D — 1, т. е. реализуется практически полное поглощение падающей мощности слоем магнетика (на толщине d — 15 мкм). При сильном поглощении величина D резко возрастает до максимального значения, после чего наблюдается менее резкий спад. Слабое поглощение, напротив, характеризуется плавным возрастанием величины коэффициента D до некоторого характерного значения насыщения.

На рис. 6 приведены зависимости коэффициента поглощения от внешнего магнитного поля, полученные для толщины слоя магнетика d = 15 мкм, отвечающей максимуму поглощения, при значениях разности фаз 8 = 0, л/4, л/3, л/2, 5л/4, л (кривые 1-6). Видно, что изменением разности фаз можно достичь как полного поглощения (кривая 1), так и практически полного его отсутствия (кривая 6), которое отвечает без-диссипативному переносу через слой падающей на него энергии.

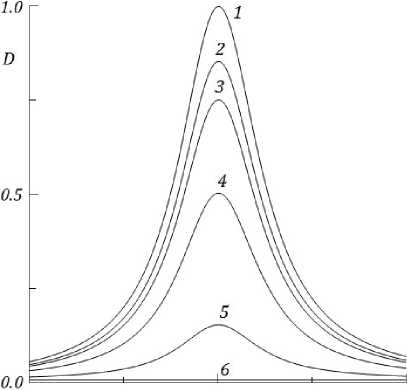
64                    72 Н, Э 80

Рис. 6. Полевая зависимость коэффициента поглощения при толщине слоя d = 15 мкм и 8 = 0, п/4, п/3, п/2, 5п/4, п (кривые 1–6)

Заключение

В работе исследованы интерференционные эффекты пропускания и поглощения при нормальном падении на противоположные границы слоя поперечно намагниченного слоя двух встречных когерентных линейнополяризованных волн. Установлено, что возможно управление как про-пускательной, так и поглощательной способностью слоя при изменении внешнего магнитного поля вблизи резонансного его значения. Для каждой величины приложенного поля из выбранного диапазона также возможна вариация указанных характеристик за счет изменения соотношения между амплитудами «сигнальной» волны и волны «подсветки», а также подбора определенной разности фаз этих волн. В исследуемых пленках максимум поглощения находится в интервале толщин 11…17 мкм. Таким образом, рассмотренные пленки микронных размеров на практике могут быть использованы как эффективные поглотители СВЧ-излучения.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 гг.