Интерполяция между инженерно-геологическими скважинами с учетом генетического типа элемента

• 1    Введение / Introduction

Для обеспечения качественного проектного и строительного процесса и представления разработанного проекта в трехмерном виде цифровое информационное моделирование (BIM) становится важным инструментом совместного проектирования и строительства [1]. Уровень развития BIM и регламентов его работы не включает моделирование инженерно-геологических условий строительной площадки, а оставляет его на уровне 2D-проектирования [2], [3]. Цифровая инженерно-геологическая модель местности является единственным нереализованным аспектом строительства, что не позволяет использовать информационное моделирование для полного цикла реализации проекта [4]. Проблемой применения в BIM геологических данных заключается в сложности извлечения информации из инженерно-геологических изысканий и инженерногеологических разрезов и последующего задания исходных данных в программных и расчетных комплексах [5].

Информационная инженерно-геологическая модель местности позволяет не допускать ошибки при проектировании, строительстве и эксплуатации за счет визуального контроля и

автоматизированных проверок в среде BIM [6], [7]. Трехмерные инженерно-геологические модели являются удобным, компактным и важным результатом представления инженерно-геологических изысканий, однако процесс построения трехмерных моделей на основе двухмерных данных остается достаточно проблематичным и не всегда надежным [8], [9]. В работах [2], [5], [10], [11] выявлено, что основной причиной отсутствия BIM для инженерной геологии является неимение программных комплексов с требующим функционалом и обеспечивающих гибкую интеграцию с расчетными комплексами. Инженерно-геологическая модель должна удовлетворять правильности сложения слоев, выдерживанию их литографии и генезиса, а геотехническая модель создана для расчетов, в связи с чем полная интеграция моделей невозможна [12]. Дополнительно отсутствуют достоверные способы проверки правильности построенных инженерно-геологических моделей, а возможное количество интерпретаций результатов геологических изысканий в формате цифровых моделей велико [13].

Трехмерное моделирование инженерно-геологических условий строительной площадки требует множество ручных операций, что связано с большим количеством неопределенности, возникающих в процессе генерации модели. В работе [14] обоснована необходимость большого количества сложных итераций задания исходных данных при построении цифровой инженерногеологической модели. Для достижения автоматизации предложен метод создания цифровой модели, основанный на построении геологических элементов в виде наборов прямоугольных треугольных призм. В результате получено, что для автоматизированного построения геологических структур с разломами или защемлением необходимо введение дополнительных скважин. Предложенный подход в исследовании [14] не учитывает горизонтальные геологические данные, литографию и генезис. В работе [15] предложен метод построения моделей, основанный на идее объединения вертикальных геологических данных (скважины или разрезы, построенные на основе скважин) и горизонтальных геологических данных (плоскостная геологическая карта). Получено, что при использовании только вертикальных данных не учитывается взаимосвязь структуры массива между разрезами, что приводит к отсутствию в модели структурного разрыва, складчатой структуры.

Инженерно-геологическая модель является описанием инженерно-геологических условий строительной площадки, однако способы верификации полученных моделей отсутствуют. В исследовании [16] выявлено, что к основным проблемам при построении трехмерных инженерногеологических моделей относят неточности исходных данных. На построение инженерногеологических разрезов влияют плотность исходных данных (количество измеряемых точек на единицу длины), результаты лабораторных испытаний и квалификация инженера. При построении трехмерных моделей существенное влияние оказывают выбранный метод моделирования, размер сетки, метод интерполяции. Неточности, полученные на этапе формирования исходных данных, напрямую влияют на корректность разрезов и моделей. С целью повышения точности исходных данных требуется проводить большее количество лабораторных экспериментов, уменьшать расстояния между инженерно-геологическими скважинами, что приведет к удорожанию строительных работ и увеличению сроков реализации проекта. С целью повышения точности построения инженерно-геологических моделей необходимо рациональное обоснование оптимального размера сетки и метода моделирования, а также применение метода интерполяции, обеспечивающего учет физических процессов образования инженерногеологических элементов (ИГЭ).

Для построения поверхности разделения ИГЭ используются методы обратно взвешенных расстояний, кригинга и радиальной базисной функции (РБФ) [17]. Перечисленные способы игнорируют неопределенности исходных данных, и полученная модель может не соответствовать действительным инженерно-геологическим условиям. В работе [18] предложен метод взвешенного кригинга для построения границ ИГЭ, использующий исходные данные, разделенные по степени достоверности на две группы – твердые (высокая степень достоверности) и мягкие (низкая степень достоверности). В результате получено, что метод взвешенного кригинга повышает точность построения моделей и позволяет интерполировать данные, собранные из нескольких источников с различными неопределенностями, однако метод взвешенного кригинга не позволяет учитывать литографию и генезис. В работах [19,20] предложен метод построения геологических слоев с применением метода РБФ. В результате доказана эффективность метода РБФ, что подтверждает возможность его применения для прогнозирования расположения ИГЭ и получения трехмерной геологической модели, однако в методе РБФ отсутствует возможность учета литографии и генезиса.

Стратиграфия для моделирования состояния недр интенсивно развивается в течение последних двух десятилетий [21]. В исследовании [22] предложен метод последовательного Гауссово моделирования грунтового массива с построением вариограмм по исходным данным и последующего прогнозирования свойств ИГЭ. В исследовании в качестве исходных данных задавались характеристики образцов, показатели пластичности и текучести грунта и происходила нормализация полученных данных. По результатам исследования [22] авторами получена трехмерная модель отложения города Керман, позволившая сделать выводы о составе почв, размерах и градации зерен в районе исследования (для точного прогнозирования потребовалось большое количество бурений на площадке – 700 скважин). Методами стратиграфии невозможно определить с высокой точностью инженерно-геологические условия строительной площадки ввиду ограничения бюджета строительства, не позволяющего выполнить достаточное количество бурений для применения стратиграфических методов построения моделей [23].

Передовой технологией в области генерации инженерно-геологических моделей является применение нейронных сетей, позволяющих с высокой точностью определять инженерногеологические условия [24]. В работе [25] представлен подход глубокого обучения графовых нейронных сетей, позволяющий выполнять построения ИГЭ. По результатам работы получено, что нейросеть способна генерировать трехмерные инженерно-геологические модели и подбирать внутренние границы ИГЭ. В работе [26] предложены сверточные нейронные сети для построения трехмерных инженерно-геологических моделей. Использование сверточных нейронных сетей позволяет предсказывать параметры геологической среды в трехмерной модели. Однако основной проблемой использования нейронных сетей при построении инженерно-геологических моделей является отсутствие исходных данных (моделей) для проведения анализа [27].

В связи с отсутствием точных и не требующих дополнительных итераций методов, которые могут учитывать литографию и генезис, разработка процедуры интерполяции результатов инженерно-геологических результатов с учетом литографию и генезис является перспективным направлением.

Целью работы является разработка процедуры интерполяции результатов инженерногеологических изысканий между скважинами.

Для достижения цели решены следующие задачи: разработан метод интерполяции результатов инженерно-геологических изысканий между скважинами, проанализировано влияние количества итераций, учета большего количества удаленных точек, весовых коэффициентов промежуточных точек на результат интерполяции, сделаны выводы о возможности задания параметров расчета для различных генетических типов отложения.

• 2    Материалы и методы / Materials and Methods

Внутренние границы ИГЭ зачастую являются плавно-изменяющимися линиями, которые описываются через единую формулу, при этом учет физических процессов образования пород, структуры и возраста невозможен. Для описания гладких и сглаженных поверхностей используется уравнение Лапласа (1).

д' ² u   d² u   _

—7 + — =0 °, d x ²   d y ²

где u - уравнение, описывающее гладкие и сглаженные поверхности; x , у - пространственные координаты.

Для каждой поверхности существуют собственные граничные условия, то есть точки, в которых известно значение функции u . При этом решение задачи в общем виде, а именно выражение функции и через координаты x , у с учетом граничных условий не представляется возможным. Для описания и нахождения значения функции и в заданных координатах x , у применяется метод нахождения приближенных решений с использованием дискретной задачи [28]. Зная значения в краевых точках, задача сводится к нахождению значений функции в других точках с заданным шагом. Тогда уравнение Лапласа записывается уравнением (2).

u ⁽ 4) = ¹ ■ ( u ( A i⁺ h ) + u ( A i + h ) + u ( ^Ajh ) ⁺ u ( A i - h ) ) ’

где i, у - координаты точек; A - точка с координатами i, j ; u (A) - значение функции в точке с координатами i, j ; h - шаг сетки.

Для нахождения решения применяется итеративный подход, на первом шаге которого для всех неизвестных точек задается любое значение, так как схема расчета является устойчивой (чаще всего используется среднее значение граничных условий или нулевое значение) [29].

Для итераций n + 1 значение функции и в точке с координатами i , j находится по формуле (3):

^ип +1 ( A /) = ¹ • ( ^un ( A i" ^h ) ^{+ u}n ( ^Ai+ h ) ^{+ u}n ( A i ^h ) ^{+ u}n ( Ai - h ) ) ,

где n - номер предыдущей итерации; u ₀ ( A j ) - первоначальное значение функции в точке с координатами i , j ; u_n ( A! ) - значение функции в точке с координатами i, j для итерации п .

Для итераций п + 1 значение функции u в точке с координатами i для плоской системы координат находится по формуле (4):

^un +1 ( A i ) = ¹ ■( ^un ( A i + h )^{+ u}n ( Ai - h ) ) •                                      (4)

• 3    Результаты и обсуждение / Results and Discussion

  3.1    Математическая зависимость процедуры интерполяции результатов инженерно-геологических изысканий

Для описания математической зависимости процедуры интерполяции результатов инженерно-геологических изысканий, позволяющей учитывать литографию и генезис ИГЭ, выражение (4), используемое в качестве приближенного решения уравнения Лапласа в плоской системе координат, преобразовано в уравнение (5):

• ^un +1 ( A i ) = ^un ( A i ) + ¹ ■ ( ( ^un ( A i + h ) — ^un ( A i ) ) ⁺ ( ^un ( A i - h ) - ^un ( A i ) ) ) ,                   (5)

где i - координата точек; u_n ( A ) - значение функции в точке с координатой i при итерации n ; h – шаг сетки.

Формула (5) идентична выражению (4) и имеет следующую трактовку – значение функции в заданной точке на текущей итерации определяется как сумма значения функции в данной точке на предыдущей итерации и среднее значение разниц между значениями функций в соседних точках на предыдущей итерации и значением функции в данной точке на предыдущей итерации.

Перейдя к данной концепции, вводится весовой коэффициент каждой соседней точки: чем больше весовой коэффициент у соседней точки, тем больше вес разницы значений функции между этой соседней точкой и заданной, и тем ближе значение в заданной точке будет к значению функции в соседней точке.

Для учета веса точек введен дополнительный весовой коэффициент, тем самым формула (5) преобразована в выражение (6):

• ^un +1 ( A i ) = ^un ( A i ) ^{+ 1} ■ ^ i + h ( ^un ( A i + h ) - ^un ( A i ) ) ^{+ 1} ■ C i - h ( ^un ( A i - h ) - ^un ( A i ) ) ,             (6)

где с - весовой коэффициент точки с координатой i .

Для учета нескольких соседних точек введен коэффициент влияния удаленности точек от рассчитываемой. Таким образом, формула (6) принимает вид (7):

• ^un+1 (Ai ) = ^un ( Ai ) ⁺      • Ё (^k^-1\^£ikkh (^un (Ai+kh ) - ^un (Ai )) ^{+ C}i-kh (^un (Ai-kh ) - ^un (Ai )))),     (7)

3.2    Влияние количества итераций и параметров расчета на профиль внутренней границы ИГЭ

2 m k =1

где ц - коэффициент, учитывающий влияние удаленности точек от рассчитываемой точки; m – количество соседних точек для учета в расчете; k – порядковый номер соседней точки, 1,2,... m .

В случае отсутствия необходимости учета коэффициента влияния удаленности точек от рассчитываемой точки (^), весового коэффициента точек (s) в формуле (7) упомянутые параметры задаются равными единице.

Для автоматизации процесса реализации данной процедуры разработан программный код на языке программирования C#, в который вошла математическая зависимость (7).

Расчет №1 выполнен с учетом влияния одной соседней точки ( m = 1 ), а также без учета коэффициента влияния удаленности точек от рассчитываемой точки ( ^ = 1 ) и весового коэффициента точек ( s = 1 ). Исходные данные (координаты точек и первоначальное значение функции), используемые для проведения расчета, приведены в таблице 1, параметры расчета представлены в таблице 2, результаты расчета приведены на рисунке 1.

Таблица 1. Исходные данные для расчета №1

Table 1. Input data for calculation №1

i , м	1	2-4	5	6-10	11	12-13	14	15	16-18	19
u 0 ( A i ) , м	3	0	7.1	0	5.2	0	3.5	3.5	0	1.3

Таблица. 2. Параметры расчета №1

Table 2. Parameters of calculation №1

Номер расчета \ Значение параметров	Обозначение на рисунке 1	h , м	n	^	m	S i
№1_1	—	1	1	1	1	1
№1_2	—	1	2	1	1	1
№1_3	—	1	5	1	1	1
№1_4	—	1	10	1	1	1
№1_5	—	1	100	1	1	1

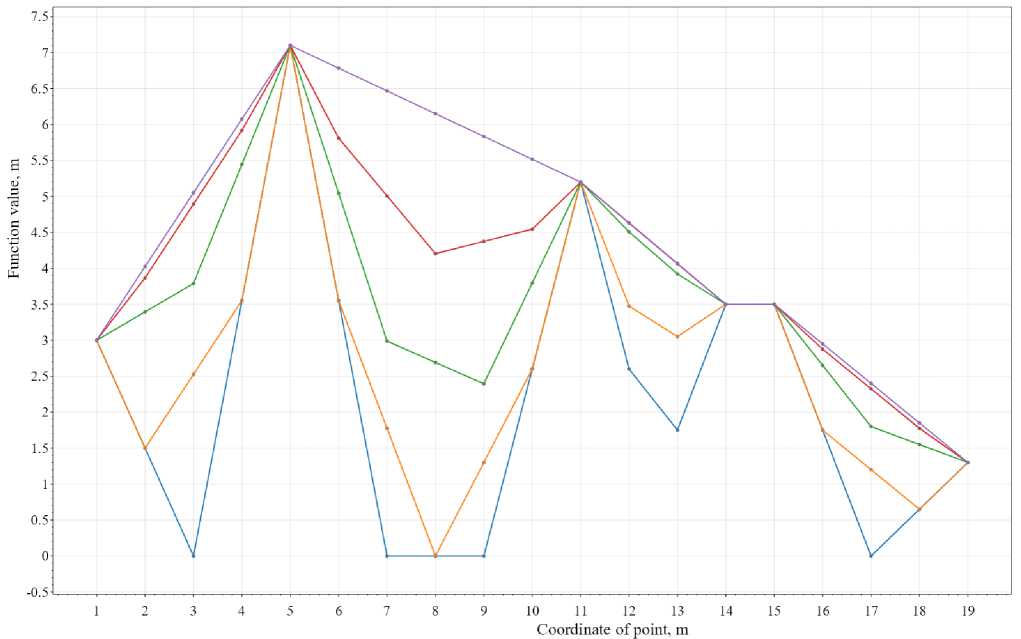
Рис. 1 – Результаты расчета №1

• Fig. 1    – Results of calculation №1

Как видно из рисунка 1, в случае учета влияния на рассчитываемую точку только одной соседней точки ( m = 1 ), а также отсутствия учета коэффициента влияния удаленности точек от рассчитываемой точки ( ^ = 1 ) и весового коэффициента точек ( ^ = 1 ) при увеличении количества итераций ( n ) график приобретает вид линии, изломанной в исходных точках (например, при n = 100 представлен окончательный вид профиля, который может быть получен при задании исходных данных, приведенных в таблице 1, и параметров расчета, приведенных в таблице 2).

Расчет №2 выполнен с учетом влияния одной соседней точки ( m = 1 ) и весовых коэффициентов точек, а также без учета коэффициента влияния удаленности точек от рассчитываемой точки ( ц = 1 ). Исходные данные (координаты точек, первоначальное значение функции и весовые коэффициенты), используемые для проведения расчета, приведены в таблице 3, параметры расчета представлены в таблице 4, результаты расчета приведены на рисунке 2.

Таблица. 3. Исходные данные для расчетов №2-№5

Table 3. Input data for calculation №2-№5

i , м	1	2-4	5	6-10	11	12-13	14	15	16-18	19
u 0 ( A i ) ■ м	3	0	7.1	0	5.2	0	3.5	3.5	0	1.3
S i	1.7	0,3	2	0.3	1.7	0.3	1.5	1	0,3	1.5

Таблица. 4. Параметры расчета №2

Table 4. Parameters of calculation №2

Номер расчета \ Значение параметров	Обозначение на рисунке. 2	h , м	n	V	m	S i
№2_1	—	1	1	1	1	0.3
№2_2	—	1	2	1	1	0.3
№2_3	—	1	5	1	1	0.3
№2_4	—	1	10	1	1	0.3
№2_5	—	1	100	1	1	0.3

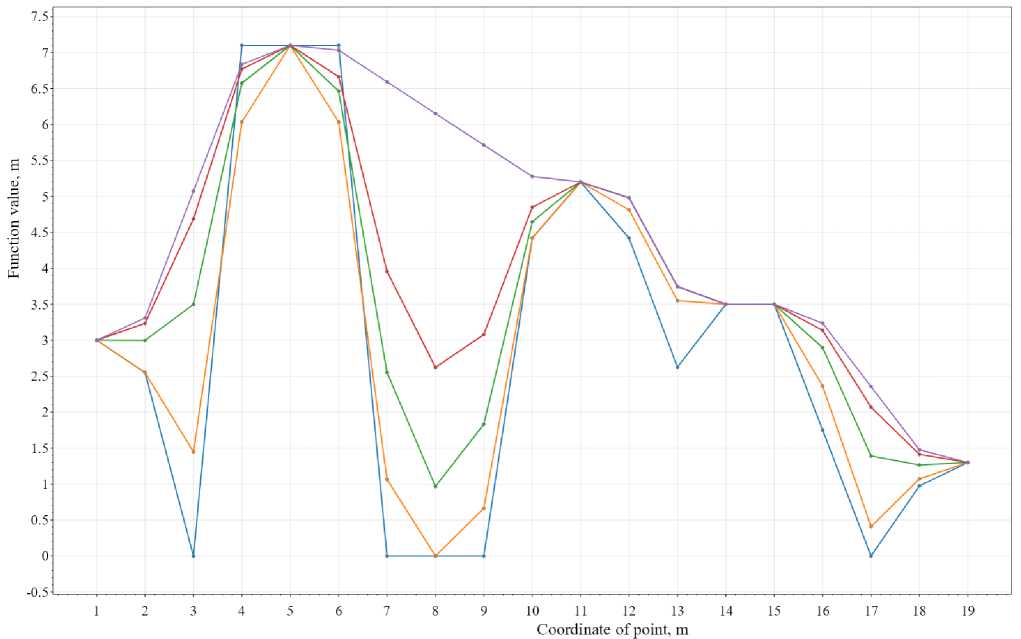
Рис. 2 – Результаты расчета №2

• Fig. 2    – Results of calculation №2

Как видно из рисунка 2, в случае учета влияния на рассчитываемую точку только одной соседней точки ( m = 1 ) и весовых коэффициентов точек, а также отсутствия учета коэффициента влияния удаленности точек от рассчитываемой точки ( ^ = 1 ) при увеличении количества итераций ( n ) график приобретает вид изломанной в исходных точках линии, сглаженной в окрестности исходных точек (например, при n = 100 представлен окончательный вид профиля, который может быть получен при задании исходных данных, приведенных в таблице 3, и параметров расчета, приведенных в таблице 4). Значение в ближайших точках к заданным вершинам стремится к значению в заданных вершинах.

Расчет №3 выполнен с учетом влияния двух соседних точек ( m = 2 ) и весовых коэффициентов точек, а также без учета коэффициента влияния удаленности точек от рассчитываемой точки ( ^ = 1 ). Исходные данные (координаты точек, первоначальное значение функции и весовые коэффициенты), используемые для проведения расчета, приведены в таблице 3, параметры расчета представлены в таблице 5, результаты расчета приведены на рисунке 3.

Таблица. 5. Параметры расчета №3

Table 5. Parameters of calculation №3

Номер расчета \ Значение параметров	Обозначение на рисунке 3	h , м	n	V	m	S i
№3_1	—	1	1	1	2	0.3
№3_2	—	1	2	1	2	0.3
№3_3	—	1	5	1	2	0.3
№3_4	—	1	10	1	2	0.3
№3_5	—	1	100	1	2	0.3

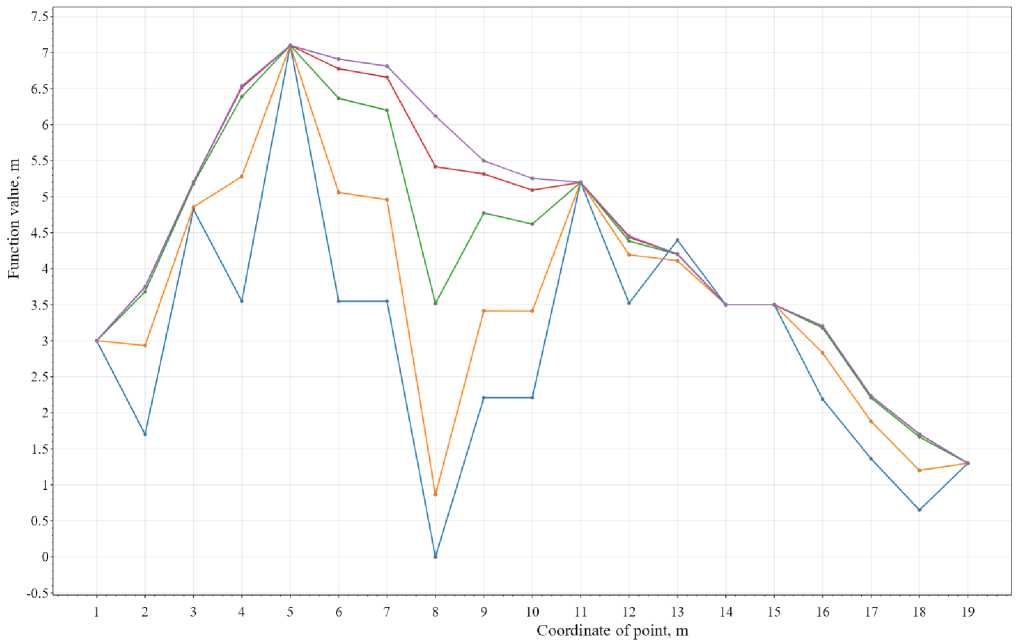
Рис. 3 – Результаты расчета №3

Fig. 3 – Results of calculation №3

Как видно из рисунка 3, в случае учета влияния на рассчитываемую точку двух соседних точек (m = 2) и весовых коэффициентов точек, а также отсутствия учета коэффициента влияния удаленности точек от рассчитываемой точки (р = 1) при увеличении количества итераций (n) график приобретает вид изломанной в исходных точках линии, сглаженной в окрестности исходных точек (например, при n = 100 представлен окончательный вид профиля, который может быть получен при задании исходных данных, приведенных в таблице 3, и параметров расчета, приведенных в таблице 5). Значение в ближайших точках к заданным вершинам стремится к значению в заданных вершинах, при этом на промежуточных и на конечной итерациях имеются изломы в линиях, связанные с учетом дальних точек, значения в которых не являются характерным для окрестности рассчитываемой точки. При этом величина окрестности сглаживания увеличилась по сравнению с результатами расчета №2_5, приведенными на рисунке 2.

Расчет №4 выполнен с учетом влияния двух соседних точек ( m = 2 ), весовых коэффициентов точек и коэффициента влияния удаленности точек от рассчитываемой точки ( р = 0,5 ). Исходные данные (координаты точек, первоначальное значение функции и весовые коэффициенты), используемые для проведения расчета, приведены в таблице 3, параметры расчета представлены в таблице 6, результаты расчета приведены на рисунке 4.

Таблица. 6. Параметры расчета №4

Table 6. Parameters of calculation №4

Номер расчета \ Значение параметров	Обозначение на рисунке 4	h , м	n	р	m	ь
№4_1	—	1	1	0.5	2	0.3
№4_2	—	1	2	0.5	2	0.3
№4_3	—	1	5	0.5	2	0.3
№4_4	—	1	10	0.5	2	0.3
№4_5	—	1	100	0.5	2	0.3

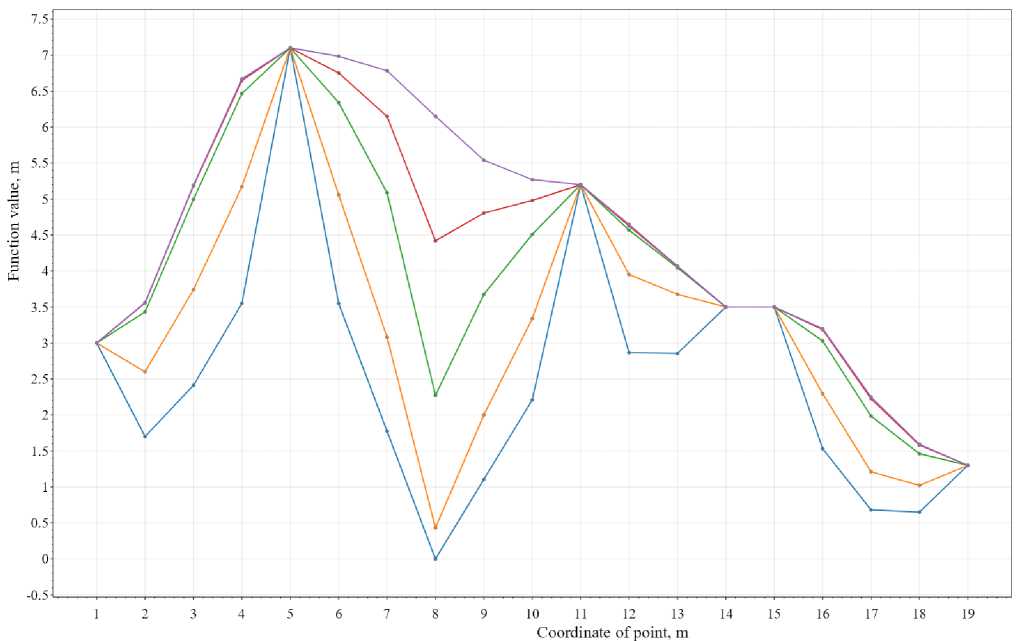
Рис. 4 – Результаты расчета №4

Fig. 4 – Results of calculation №4

Как видно из рисунка 4, при учете влияния на рассчитываемую точку двух соседних точек (m = 2), весовых коэффициентов точек и коэффициента влияния удаленности точек от рассчитываемой точки (р = 0,5) при увеличении количества итераций (n ) график приобретает вид изломанной в исходных точках линии, сглаженной в окрестности исходных точек (например, при n = 100 представлен окончательный вид профиля, который может быть получен при задании исходных данных, представленных в таблице 3, и параметров расчета, приведенных в таблица 6). Значение в ближайших точках к заданным вершинам стремится к значению в упомянутых вершинах, при этом на промежуточных и на конечной итерациях отсутствуют изломы в линиях, что связанно с понижающим коэффициентом учета дальних точек, значение в которых не является характерным для окрестности рассчитываемой точки (по сравнению с расчетом №3_5, представленным на рисунке 3). При этом величина окрестности сглаживания увеличилась по сравнению с результатами расчета №2_5, приведенными на рисунке 2, и осталась неизменной по сравнению с результатами расчета №3_5, приведенными на рисунке 3.

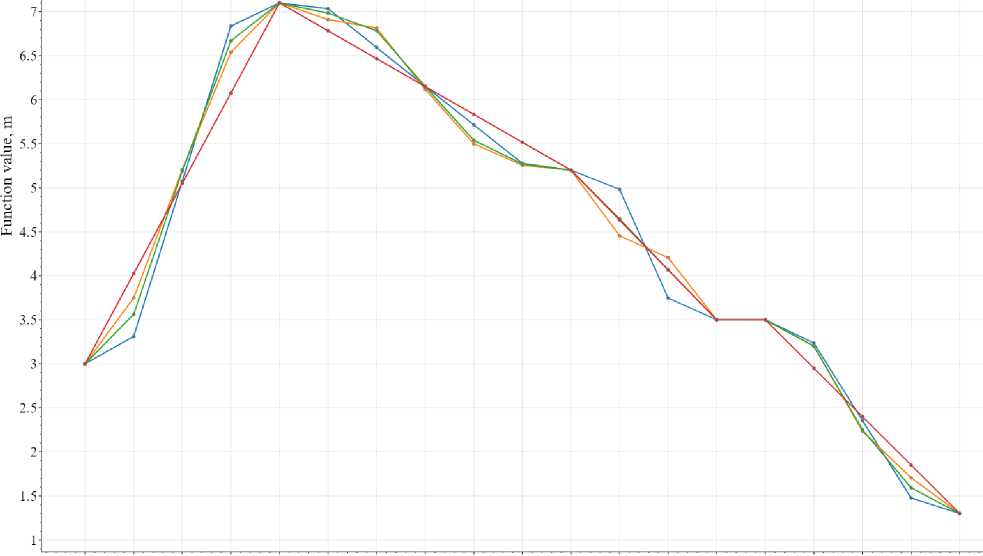
На рисунке 5 представлено сравнение конечных результатов при n = 100 для расчетов с различными параметрами. Исходные данные (координаты точек, первоначальное значение функции и весовые коэффициенты), используемые для проведения расчета, представлены в таблице 2 (для расчета №1_5) и таблице 3 (для расчетов №2_5 - №4_5), параметры расчета приведены в таблице 7.

Таблица. 7. Сравнение расчетов №1-№4 при итерации n = 100

Table 7. Comparison of calculations №1-№4 at iteration n = 100

Номер расчета \ Значение параметров	Обозначение на рисунке 5	h , м	n	V	m	^
№4_5	—	1	100	0.5	2	0.3
№3_5	—	1	100	1	2	0.3
№2_5	——	1	100	1	1	0.3
№1_5	—	1	100	1	1	1

7.5

1       2       3       4       5       6       7       8       9       10      11      12      13      14      15      16      17      18      19

Coordinate of point, m

Рис. 5 - Сравнение расчетов №1-№4 при итерации n = 100

Fig. 5 - Comparison of calculations №1-№4 at iteration n = 100

Как видно из рисунка 5, наилучший результат достигнут при выполнении расчетов №4_5 и №2_5 (таблица 7). Результат расчета №1_5 определяется линией, изломанной в исходных точках без окрестности сглаживания, а результат расчета №3_5 определяется линией с изломами, обуславливающими отсутствие плавности профиля. У линии, описывающей результаты расчета №2_5, соседние точки от заданных вершин имеют значение ближе к заданным в сравнении с Kudryavtsev, V..; Radaev, A..; Gravit, M.

Interpolation between engineering-geological wells with consideration of the genetic type of the element;

линией, соответствующей результатам расчета №4_5, что связано с учетом большого количества соседних точек в расчете №4_5. При этом линия, описывающая результаты расчета №2_5, содержит изломы только в соседних точках от заданных вершин, в других областях точки выстраиваются в прямую линию аналогично результатам расчета №1_5, что объясняется одинаковым значением весового коэффициента промежуточных точек для упомянутых расчетов.

3.3 Параметры расчета для различных генетических типов отложений

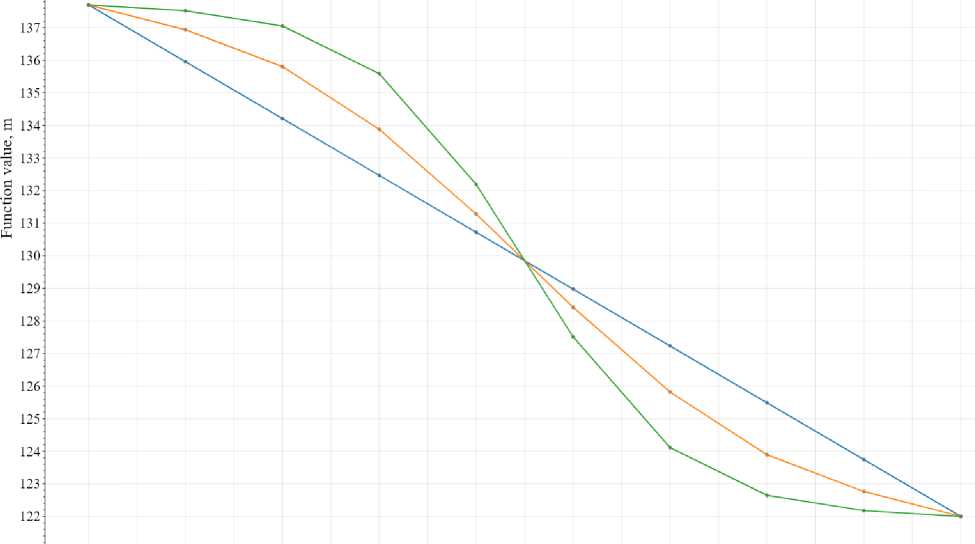
Расчет №5 выполнен с учетом влияния переменного количества соседних точек, весовых коэффициентов точек и коэффициента влияния удаленности точек от рассчитываемой точки с целью демонстрации возможности описания различных генетических типов отложений разработанной процедурой интерполяции. Исходные данные (координаты скважин, отметка залегания и весовой коэффициент ИГЭ), используемые для проведения расчета, приведены в таблице 8, параметры расчета представлены в таблице 9, результаты расчета приведены на рисунке 6.

Таблице. 8. Исходные данные для расчета №5

Table 8. Input data for calculation №5

№ Скважины	1	2
Отметка устья, м	137.7	122
Расстояние между скважинами, м	10

Таблице. 9. Параметры расчета №5

Table 9. Parameters of calculation №5

Номер расчета \ Значение параметров	Обозначение на рисунке 6	n	µ	m	ε i
1	—	15000	1	1	1
2	—	15000	0.5	10	0.1
3	—	15000	0.5	20	0.01

1       1.5       2       2.5       3       3.5       4       4.5       5       5.5       6       6.5       7       7.5       8       8.5       9       9.5       10

Coordinate of point, m

Рис. 6 – Результаты расчета №5

Fig. 6 – Results of calculation №5

Как видно из рисунка 6, для генетических типов, характеризующихся плавным изменением границ ИГЭ (озерные, морские и болотные отложения), необходимо задавать меньшее количество соседних точек при расчете и большие значения весового коэффициента Kudryavtsev, V..; Radaev, A..; Gravit, M.

Interpolation between engineering-geological wells with consideration of the genetic type of the element;

промежуточных точек, чем для генетических типов, характеризующихся резким изменением границ ИГЭ (гравитационные осыпные отложения, горные породы, преимущественно залегающие складчатой формой, и отложения, верхняя граница которых сформировалась благодаря движению ледника).

Таким образом, разработанная процедура позволяет получать внутренние границы для различных генетических типов ИГЭ с учетом литографии и генезиса. В исследовании [18] для получения внутренних границ ИГЭ используется метод взвешенного кригинга, в работе [19,20] предложен метод построения геологических слоев с применением метода РБФ, но при этом в рассмотренных методах отсутствует возможность задания литографии и генезиса, что не позволяет получить корректные инженерно-геологический разрезы и модели. В работах [25,26,30] представлен подход глубокого обучения нейронных сетей для построения инженерногеологических моделей. Основной сложностью использования нейронных сетей при построении инженерно-геологических моделей является отсутствие исходных данных (моделей) для проведения анализа. Таким образом, предложенная процедура интерполяции результатов инженерно-геологических изысканий между скважинами позволяет учитывать особенности происхождения, залегания и типа ИГЭ при построении инженерно-геологических разрезов и моделей.

• 4 Выводы / Conclusions

В связи с отсутствием точных и не требующих дополнительных итераций методов, которые могут учитывать литографию и генезис, разработка процедуры интерполяции результатов инженерно-геологических результатов с учетом литографии и генезиса характеризуется высокой теоретической и практической значимостью. По результатам исследования получены следующие результаты:

• 1.    разработана процедура интерполяции результатов инженерно-геологических изысканий между скважинами;

• 2.    произведена оценка влияния параметров расчета: количество итераций, коэффициента влияния удаленности точек от рассчитываемой и весовых коэффициентов промежуточных точек, количество учитываемых точек при расчете;

• 3.    проанализирована возможность задания различных форм залегания ИГЭ при помощи разработанной процедуры.

По результатам анализа разработанной процедуры интерполяции результатов инженерногеологических изысканий между скважинами получены следующие результаты:

• 1.    совокупность параметров: количество соседних точек, весовые коэффициенты промежуточных точек и коэффициент влияния удаленности точек от рассчитываемой позволяют получать достаточно большое количество вариантов видов внутренних границ ИГЭ разного генезиса (плавное и резкое изменение границ элементов);

• 2.    наилучший результат достигнут при применении коэффициента влияния удаленности точек от рассчитываемой точки, весовых коэффициентов промежуточных вершин и при задании количества удаленных точек для учета значения в текущей точке;

• 3.    при увеличении количества итераций внутренняя граница перестает изменяться и принимает окончательный вид.

Разработанная процедура интерполяции результатов инженерно-геологических изысканий между скважинами может быть использована при автоматизированном процессе построения инженерно-геологических разрезов и моделей.

• 5 Благодарности / Acknowledgements