Интерполяция расчётных полей на многоблочных структурированных сетках для численного моделирования трёхмерного обтекания стреловидного крыла
Автор: Горякин А. А.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Механика
Статья в выпуске: 2 (58) т.15, 2023 года.
Бесплатный доступ
Представлена программа для интерполяции трехмерных полей течения между многоблочными структурированными расчётными сетками. Используется метод трилинейной интерполяции, для поиска ячейки с исходными данными применяется R-дерево. Разработанная программа протестирована на примере задачи моделирования трехмерного обтекания стреловидного крыла с использованием двух видов расчётных сеток: «грубой» и подробной. Поле, интерполированное с «грубой» на подробную сетку, используется в качестве начального приближения для дальнейшего расчёта. Показана эффективность такого подхода для получения результирующего поля, за счёт сокращения машинного времени расчёта.
Интерполяция, вычислительная аэродинамика, расчетные сетки, начальное приближение
Короткий адрес: https://sciup.org/142238150
IDR: 142238150 | УДК: 519.652
Текст научной статьи Интерполяция расчётных полей на многоблочных структурированных сетках для численного моделирования трёхмерного обтекания стреловидного крыла
В последние годы решение задач аэродинамики основывается на. использовании прямого численного моделирования. Чаще всего оно осуществляется решением полных уравнений Навье-Стокса. с минимальным количеством упрощений. К таким задачам относятся также задачи, направленные на изучение механизмов ламинарно-турбулентного перехода.
Использование численного моделирования при исследовании течений в пограничном слое позволяет получать решения более детальные и повторяемые, а также более дешевые
«Московский физико-технический институт (национальный исследовательский университет)», 2023
нежели результаты, полученные при проведении экспериментов с использованием аэродинамических труб. Однако для численного моделирования течений в пограничном слое необходимо использовать подробные расчётные сетки, которые содержат сотни миллионов ячеек, из-за чего вычислительный процесс требует колоссального количества вычислительных ресурсов. При этом основную часть времени моделирования, в зависимости от необходимой точности, занимает расчёт базового поля стационарного ламинарного обтекания, на основании которого затем развиваются нестационарные возмущения. Исходя из этого, время и ресурсы, требуемые для генерации базового поля, необходимо сокращать.
Одним из способов решения данной задачи является подход последовательного измельчения расчётной сетки. Изначально вычисление проводится на грубой сетке с малым количеством ячеек, на ней строится поле обтекания. Затем проводится процесс интерполяции полученного решения на более подробную сетку с большим количеством ячеек. После этого продолжаются вычисления на подробной сетке вплоть до получения целевого подробного решения. В данном случае суммарное время решения оказывается меньше, чем в случае полного расчёта на подробной сетке. Однако для полной реализации данного рабочего процесса необходимо программное средство, позволяющее провести интерполяцию дискретных полей между грубой и подробной расчётными сетками. В статье [1] описан инструмент, позволяющий эффективно производить интерполяцию между двумерными расчётными сетками.
Настоящая статья посвящена разработке инструмента интерполяции полей между расчётными сетками разной степени грубости. Рассматривается проблема интерполяции трёхмерного поля с одной многоблочной структурированной сетки на другую, описываются основные шаги алгоритма интерполяции и особенности его реализации. Применимость разработанной программы интерполяции продемонстрирована на примере задачи моделирования стационарного сверхзвукового обтекания. Оценивается время расчёта поля обтекания с различными начальными приближениями и сравниваются поля обтекания и профили пристенного течения для основного и интерполированного полей.
2. Постановка задачи
Ставится задача интерполяции трехмерного дискретного поля течения, рассчитанного на исходной многоблочной сетке на целевую многоблочную сетку, с иным разбиением и количеством блоков и узлов. В качестве тестового примера рассматривается стреловидное крыло бесконечного размаха с нулевым углом атаки и углом скольжения х = 30° и хордой с = 0.3 м. Схема конфигурации и системы координат показана на рис. 1, а схема аэродинамического профиля крыла - на рис. 2.
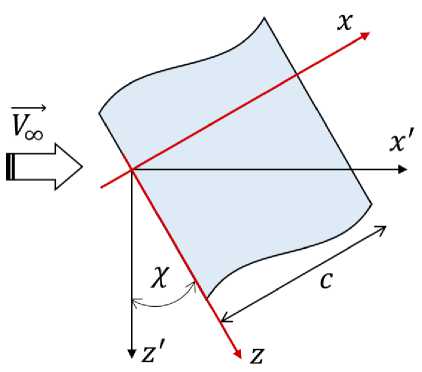
Рис. 1. Схема, скользящего крыла, бесконечного размаха, в плане и оси координат
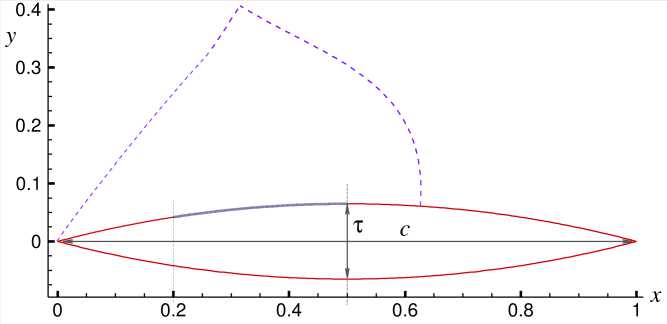
Рис. 2. Схема профиля крыла (сплошная линия) и граница расчётной области (пунктирная линия)
Задача решается на структурированных многоблочных криволинейных сетках, т.е. таких сетках, в которых множество узлов упорядочено таким образом, что в соответствие каждому узлу можно поставили индексы (i,j,k ), и соседние узлы по каждой оси имеют индексы, отличающиеся на единицу. Ячейки в данных сетках имеют форму параллелепипедов, вершины которых соответствуют узлам сетки. Так как сетки криволинейные, то у ячеек не предполагается параллельность и равенство сторон. Для трехмерного случая схематично такая сетка изображена на рис. 3, где сплошными линиями показаны блоки сетки, а пунктирными - ячейки, расположенные в этих блоках.
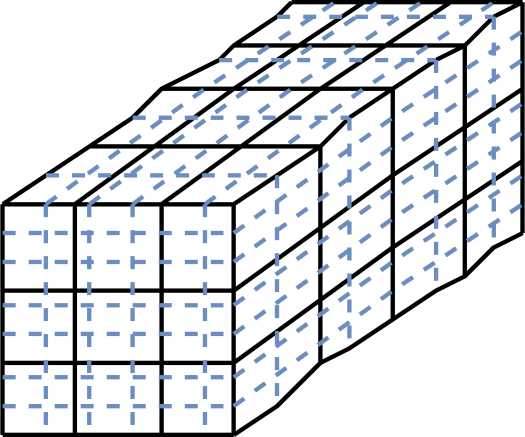
Рис. 3. Схематичное изображение многоблочной структурированной сетки
Для нахождения значений в каждом узле такой сетки необходимо интерполировать значения величин из ближайших узлов исходной сетки. В качестве этих узлов можно взять узлы ячейки исходной сетки, в которую попал указанный узел целевой сетки. Тем самым приходим к следующему общему алгоритму интерполяции:
1) Обходим все блоки целевой сетки.
2) В каждом блоке обходим все узлы и для каждого узла находим ячейки исходной сетки, в которую может попасть указанный узел.
3) Для каждой найденной ячейки проверяем попадание узла в неё. Если узел попадает, возвращаем эту ячейку.
4) В найденной ячейке интерполируем значения всех полей для заданного узла.
2.1. Поиск ячеек исходной сетки
2.2. Определение принадлежности узла ячейке
Данная методика уже использовалась в статье [1] для интерполяции двумерных полей. Отличие состоит только в способе проверки попадания узла в ячейки и способе интерполяции значения.
В текущей работе представлен трехмерный случай. Рассмотрим по порядку шаги алгоритма (2-4).
Поиск ячейки и блока исходной сетки является самым трудоемким шагом алгоритма. Существует несколько способов решения данной проблемы. Рассмотрим два из них.
Первый способ - решение задачи «в лоб». Он основан на полном переборе всех ячеек и проверки для каждой ячейки принадлежности узла целевой сетки. Этот способ является очень долгим, т.к. в худшем случае необходимо перебрать все ячейки исходной сетки, а суммарный объем необходимых операций равен произведению количества ячеек исходной (Ns) и целевой (Nt) сеток. Тем самым сложность алгоритма можно оценить как O(NS х Nt)
Однако существует еще один способ решения данной проблемы, который основан на использовании структуры хранения пространственных данных, а именно R-дерева (см. [8]). Оно основано на В-дереве поиска и хранит в себе декартово разбиение пространства на параллелепипеды, являющиеся описывающими параллелепипедами каждой из ячеек исходной сетки (см. п. 2.3). Сложность такого алгоритма можно оценить как O(logNs). Именно этот подход и используется в текущей работе.
Для того чтобы интерполировать значение внутри исходной ячейки, необходимо удостовериться, что узел попадает в границы ячейки. В трёхмерном случае воспользуемся способом определения, основанным на векторном произведении. Для этого надо провести процедуру, которая проверяет, что векторы от каждой грани ячейки до узла смотрят внутрь ячейки. Предположим, что у нас есть одна из граней ячейки, которая состоит из точек Р1, Р2, Р3, Р4 С координатами (жі , У1,21), (Х2,У2,22) (жз,Уз, 23), (і4,У4,24) соответственно. Также у нас есть точка в пространстве с координатами (x,y,z) и некоторая константа, которая показывает нам минимальную погрешность (10-15), при которой мы считаем, что точка не попадает в ячейку. Пример показан на рис. 4.
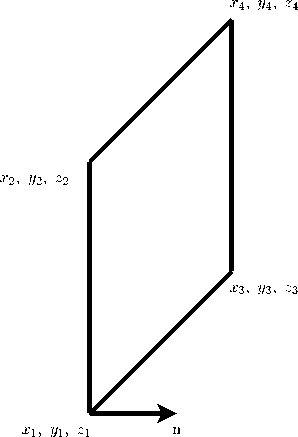
Рис. 4. Пример на основе одной из граней ячейки
Ж, У, 2
Тогда процедура реализуется с помощью проверки векторного произведения векторов по формулам:
е = 10-15,
Ф = (X1 - X,y1 - y, 21 - 2) = (Vx,Vy,Vz),
Ф = ус^Т+гІ+г2),
ф
41 = (X2 -X1,y2 - У1,22 - 21) = (xd1,yd1,Zd1), ф
42 = (X3 -Х1,уз - У1,23 - 21) = (Xd2,yd2,2d2),
П = (yd1 X 2d1 - yd2 X 2d2, 2d1 X Xd1 - 2d2 X Xd2,Xd1 X yd2 - Xd2 X yd1) = (пх,Пу ,nz ),
nl = (П^ + пУ + n2), n = (nx /пі ,ny /пі ,nz/пі),
4 = vx X nx + Vy X ny + vz X nz ,
4 = 4/lx,
4 < E.
Данная процедура повторяется для всех граней и на выходе дает информацию о положении точки относительно ячейки. Оценим сложность данного шага алгоритма, как 0(1).
Тем самым на предпоследнем шаге алгоритма мы проверяем нахождение узла внутри ячейки. Если узел находится внутри ячейки, то переходим к последнему шагу алгоритма - интерполяции значений.
2.3. Интерполяция значений
В трёхмерном случае ячейка представляет собой искажённый параллелепипед. В общем случае форма ячейки является неправильной, т.е. ребра могут быть не параллельны и отличаться по размеру. Однако вокруг каждой такой фигуры можно построить ограничивающий параллелепипед, также показанный пунктиром на рисунке. Именной такой параллелепипед и используется для быстрого предварительного поиска ячейки по заданным координатам в п 2.1. Пример показан на рис. 5.
С011
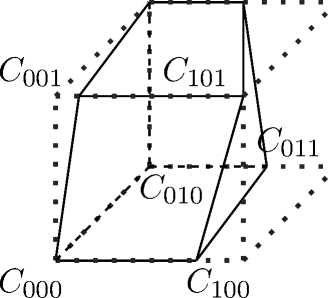
Рис. 5. Ячейка, сетки и ограничивающий прямоугольник
Ст
Для интерполяции полей внутри ячейки используется метод трилинейной интерполяции (см. [7]):
-
Ж 0 — Жтіп>
-
Ж1 — Жтах,
-
У 0 — Утіп,
-
У1 — Утах,
-
20 — ^min,
-
21 — 2тах,
Ж — Жо Xd —,
-
Ж1 — Жо
_ У — Уо yd — ,,
-
У1 — Уо(2)
-
2 — 2о
-
2d —,
21 — 20
-
С00 — С000 X (1 — Xd) + С100 X Xd,
С01 — С001 X (1 — Xd) + С101 X Xd,
-
С10 — С010 X (1 — Xd) + С110 X Xd,
С11 — С011 X (1 — Xd) + Сщ X Xd,
Со — Соо X (1 — Уd) + С10 X Уd,
С1 — С01 X (1 — Уd) + С11 X Уd,
С — Со X (1 — 2d) + С1 X 2d, где Сооо, С001, С010, Ош, Щоо, сШ1, ецо, С111 - значения в узлах ячейки, а
Жтіп, Утіп, 2min, Жтах, Утах, 2тах - минимальные и максимальные значения координат по каждой из осей.
Тем самым в рамках последнего шага алгоритма получаем в узле значения всех газодинамических функций J — {n, v,w,p, Т} через вершины найденной ячейки. Точность данного метода интерполяции составляет о(^1). Сложность этого шага алгоритма можно оценить как 0(1).
Таким образом, общая сложность алгоритма интерполяции составляет G(Nt X log Ws).
2.4. Программная реализация
Аналогично [1] для реализации инструмента интерполяции применен язык, Golang, поддерживающий кооперативную многозадачность, что позволяет очень эффективно распараллеливать вычисления с помощью горутин.
Входные и выходные данные интерполятора представляют собой дискретные поля и сетки, которые представлены бинарными файлами в формате CGNS, который является международным стандартом хранения данных в задачах вычислительной аэродинамики. В настоящей работе применяются файлы со структурированными многоблочными сетками, генерируемыми авторским пакетом расчётных программ.
Для поиска ячеек используется хранилище Tarantool, поддерживающее индексацию на основе деревьев: В+*-дерева и R-дерева (пространственная индексация). Все данные хранятся в оперативной памяти, поэтому доступ к ним происходит очень быстро и поиск проходит практически моментально. Для обеспечения быстрого поиска необходимой ячейки, данные обо всех ячейках исходной сетки помещаются в таблицу в Tarantool в формате
{ib,ic, [жтіп, Утіп, 2тіп, Жтах, Утах, 2тах]}, где ib - индекс блока сетки, ic - индекс ячеЙКИ В блоке, Жтіп, Утіп, 2тіп, Жтах, Утах, 2тах - минимальные и максимальные координаты прямоугольного параллелепипеда, ограничивающего ячейку. По полю в формате, содержащем координаты параллелепипеда, строится пространственный индекс, который используется для проверки, попадает точка в ячейку и на ее границу или нет. Для этого запускается хранимая процедура, которая ищет и отфильтровывает необходимые ячейки. На выходе возвращается список пар {гь,гс}, описывающих потенциальные ячейки, в которые может попасть точка, после чего происходит проверка попадания в каждую ячейку, которая выполняется параллельно.
После нахождения необходимой ячейки происходит интерполяция значений в целевом узле на основе значений в узлах исходной сетки.
3. Моделирование обтекания стреловидного крыла с применением программы интерполяции
В качестве примера применим разработанную программу интерполяции в задаче моделирования стационарного ламинарного обтекания стреловидного крыла трехмерным потоком газа. Выполним несколько расчетов поля обтекания: на грубой сетке, на подробной сетке и на подробной сетке, взяв за начальное приближение поле, интерполированное с грубой сетки на подробную. После этого измерим и сравним суммарное время вычислений и оценим качество интерполяции.
3.1. Постановка задачи моделирования
В задаче рассматривается трехмерное сверхзвуковое обтекание стреловидного крыла с углом скольжения 30° и характеристиками набегающего потока:
-
• Число Маха М ю = 2.0.
-
е Число Рейнольдса Reос = 9 х 106.
-
• Показатель адиабаты у = 1.4.
-
• Число Прандтля Рг = 0.72.
-
• Статическая температура набегающего потока Т^ = 161 К.
Обтекаемая поверхность является изотермической с температурой Т* = 290 К. Здесь и далее верхний индекс * означает размерные величины.
Численное моделирование обтекания проводилось путем численного решения полных уравнений Навье - Стокса в консервативном безразмерном виде для трехмерных сжимаемых течений вязкого совершенного газа. При этом в каждом узле расчетной сетки, построенной для заданной области, вычисляется пять безразмерных газодинамических величин:
-
• Декартовы компоненты вектора скорости u, v,w.
-
• Давление р.
-
• Статическая температура Т.
Декартовы компоненты скорости нормированы на скорость в набегающем потоке U *, давление обезразмерено на удвоенный скоростной напор p^U *2, а температура нормирована на Т^. Профиль крыла является симметричным в виде дуг окружностей с относительной толщиной т = 0.13 с и острой передней кромкой.
Расчет поля производится авторским пакетом программ [3], реализующим неявный метод конечного объема со сквозным счетом и аппроксимацией второго порядка по пространству и времени в рамках квазимонотонной ТVD-схемы. При приближенном решении задачи распада разрыва используется метод Роу. Для реконструкции зависимых значений на границах ячеек сетки используется подход WENO3, эффективно выполняющий аппроксимацию по пространству третьего порядка. Расчётная область, включающая в себя верхнюю левую четверть профиля крыла, показана на рис. 6.
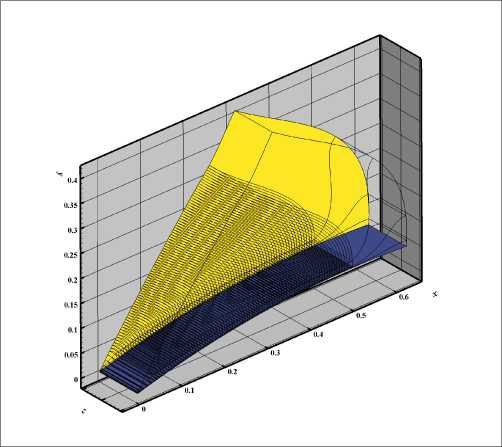
Рис. 6. Расчётная область. Черные линии показывают границы расчётных зон
Пример расчитанного поля скорости в плоскости (х,у ) и поля давления на поверхности приведены на рис. 7. Внутри области построена расчетная сетка, являющаяся ортогональной, структурированной и криволинейной. Сетка содержит 356 блоков. Рассматривается два варианта сетки - «грубая» из 631 х 201 х 5 узлов и «подробная» из 4451 х 201 х 5 узлов, что в 7.1 раза больше, в направлении вдоль крыла. Вблизи обтекаемой поверхности сетка сгущается так, чтобы примерно 100 эквидистантных сеточных линий приходится на толщину пограничного слоя. Фрагменты сеток приведены на рис. 8, жирными линиями показана грубая сетка, а тонкими - подробная.
На границах расчетной области поставлены следующие условия:
-
• На обтекаемой поверхности - изотермичность и прилипание.
-
• Набегающий поток на входной и верхней границах.
-
• Внутри расчетной области для зависимых переменных на выходной границе - линейная экстраполяция.
-
• Однородный поток или интерполированное поле в качестве начального приближения.
Инструмент интерполяции был протестирован с помощью нескольких расчётов:
1 ) Моделирование поля обтекания на грубой сетке (631 х 201 х 5), начальное приближение - однородный поток (Mc,u - modelling, coarse-uniform).
2 ) Моделирование поля обтекания на подробной сетке (4451 х 201 х 5), начальное приближение - однородный поток (Mf,u - modelling, fine-uniform).
3 ) Интерполирование поля полученного на грубой сетке в случае (Mc,u), на подробную (Ic,f - interpolating, coarse-fine).
4 ) Моделирование поля обтекания на подробной сетке (4451 х 201 х 5), начальное приближение - интерполированное поле (Мщ - modelling, fine-interpolated).
3.2. Результаты моделирования и оценка эффективности интерполяции
Для каждого случая вычисление поля обтекания проводилось по методу установления с помощью моделирования развития течения по времени с заданного начального приближения до достижения неизменяющегося стационарного поля с невязкой 10-3. Вычисления выполнялись на кластере на базе процессора Intel Xeon Е5-2670 под управлением операционной системы CentOS 7.
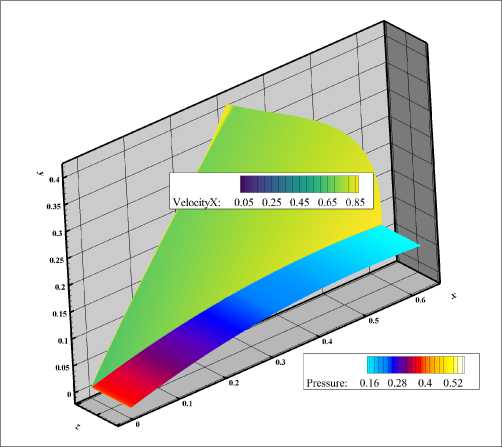
Рис. 7. Поле скорости в плоскости (ж, у ) и поле давления на поверхности
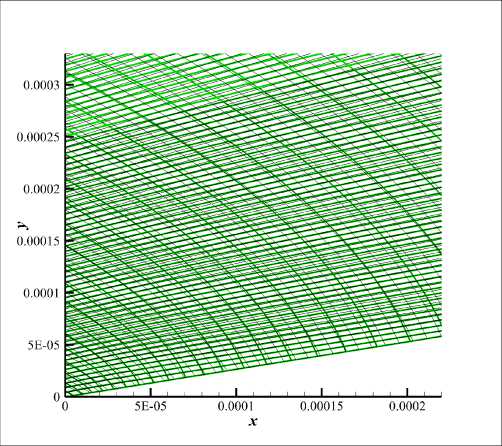
Рис. 8. Сопоставление грубой (толстые линии) и подробной (тонкие линии) расчётных сеток
Распределение давления на поверхности на стреловидном крыле представлено на рис. 9 на примере поля безразмерного давления.
Локальные особенности течения на крыле и сохранение их после интерполяции продемонстрированы на рис. 9 и 10. Приведены поля, полученные в результате расчёта Мс,и на «грубой» сетке и в результате интерполяции Icj этого поля с «грубой» сетки на подробную Mf,}. Можно отметить, что визуально картины полей выглядят идентично.
На рис. 11 и 12 показаны поля в плоскости (ж, у ) и на поверхности для температуры и давления.
Сравнение полей, полученное в результате различных расчётов, выполняется путём сопоставления распределений газодинамических величин вдоль поверхности и по нормали к поверхности в различных сечениях по продольной координате. В качестве примера на рис. 13 приводятся распределения безразмерного давления вдоль поверхности крыла, а на рис. 14 профили скорости для полей, которые были получены путём расчета на «грубой» сетке, путем интерполяции с «грубой» сетки на подробную и путем расчёта на подробной сетке. Видно, что интерполированные значения практически совпадают с теми, что были получены при расчёте на «грубой» и подробной сетках. На рис. 14 можно заметить дефекты интерполяции, которые, однако, не мешают получению корректного решения на подробной сетке.
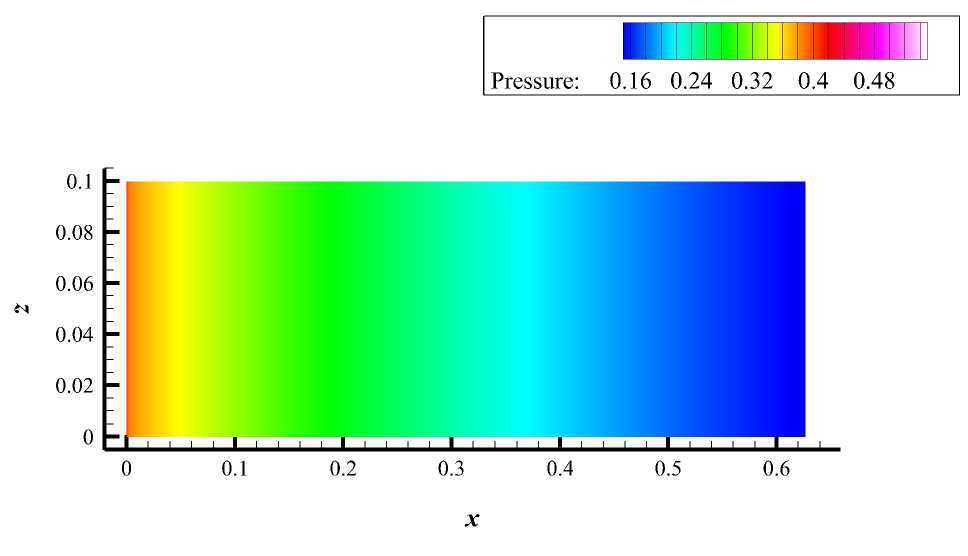
Рис. 9. Поле давления на стреловидном крыле
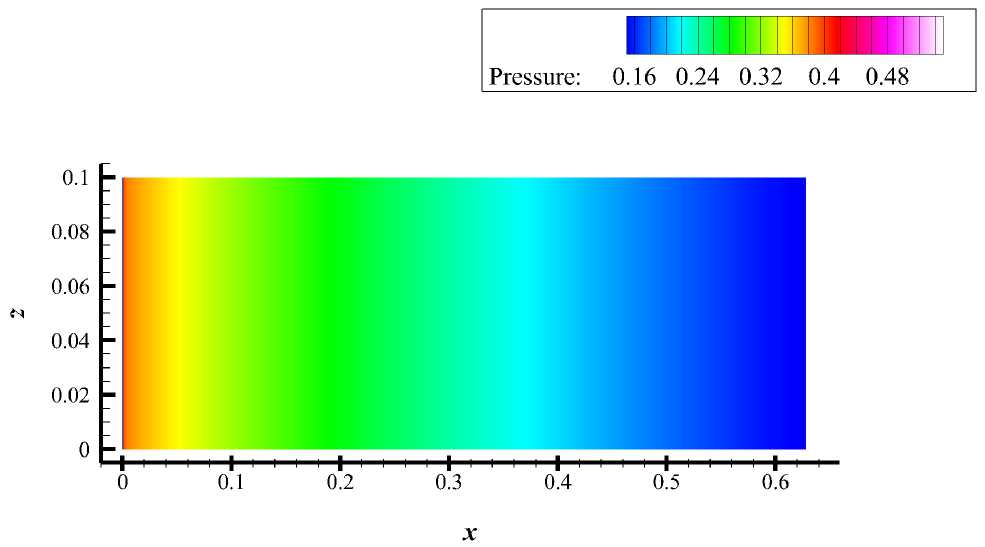
Рис. 10. Поле давления, интерполированное на подробную сетку
Практическая польза интерполяции заключается в значительном сокращении времени расчёта поля обтекания на подробной сетке. В таблице ниже представлены замеры машинного времени на кластере с процессором Intel Xeon Е5-2670, суммарно использовано 128 ядер.
Из табл. 1 видно, что применение последовательности:
-
• моделирование на «грубой» сетке,
-
• интерполяция на подробную сетку,
-
• моделирование на подробной сетке
позволяет сократить время расчёта более чем в полтора раза, что позволяет говорить о высокой эффективности такого подхода и полезности разработанного инструмента интерполяции.
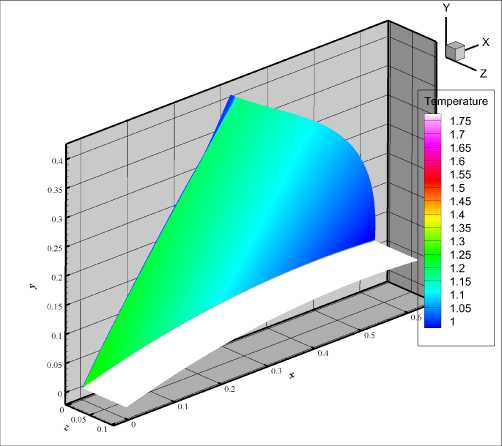
Рис. 11. Поле температуры в плоскости (х,у ) и на поверхности
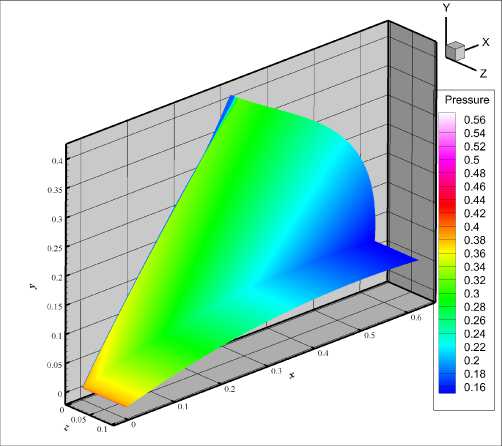
Рис. 12. Поле давления в плоскости (х, у) и распредление на поверхности
Таблица!
Длительность расчётов
|
Расчёт |
Время, с |
Относительное время |
|
М |
66269.1 |
0.419 |
|
Mf,u |
158348.4 |
1.0 |
|
Қи |
736.9 |
0.0047 |
|
Mf. |
35613.7 |
0.225 |
|
Мс,и + Қи + Mf^ |
102619.7 |
0.648 |
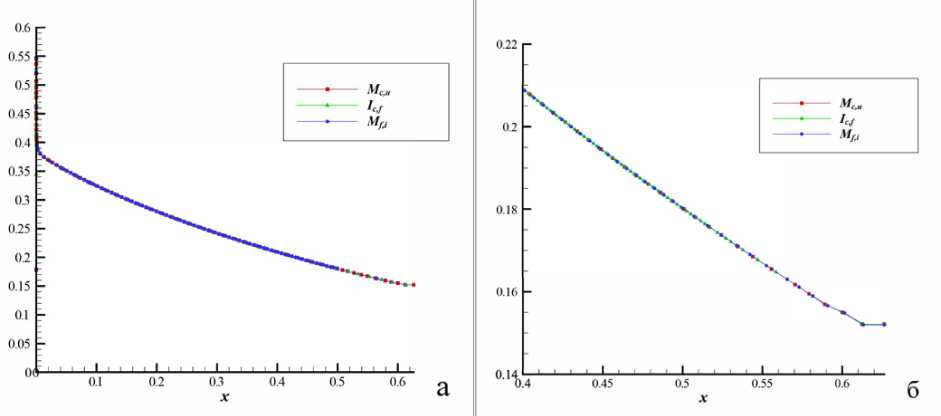
Рис. 13. Распределение давления вдоль поверхности крыла: а - полное, б - увеличенное
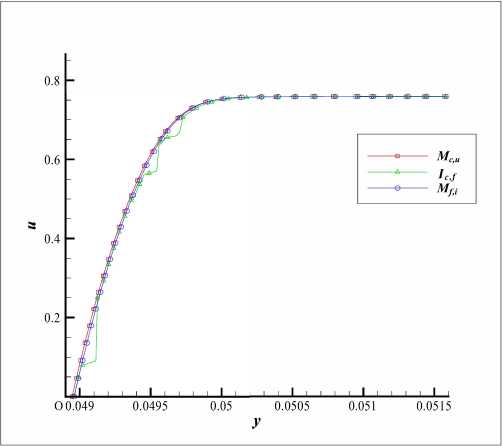
Рис. 14. Профили скорости (вдоль оси ОХ, х = 0.25)
4. Выводы
Разработан инструмент для интерполяции трехмерных расчётных полей на структурированных многоблочных расчётных сетках. В качестве метода интерполяции выбран алгоритм трилинейной интерполяции. Поиск ячеек на исходной сетке построен с использованием R-деревьев.
Инструмент интерполяции реализован на языке программирования Golang. Интерполяция производится параллельно и многопоточно. В качестве хранилища метаинформации о ячейках исходной сетки используется in-memory платформа Tarantool.
Произведено тестирование разработанного инструмента на примере задачи моделирования сверхзвукового трехмерного обтекания стреловидного крыла. Расчет проведен с применением двух расчётных сеток: грубой и подробной с большим (в 7.1 раза) числом узлов. Моделирование проведено с использованием авторского пакета программ на основе численного решения уравнений Навье - Стокса. Показано, что интерполяция полей с грубой сетки на подробную корректно сохраняет все особенности течения в области отрыва. Также применение многостадийного метода моделирования обтекания существенно сокращает время расчёта, что делает его использование практически оправданным. В рассмотренной задаче время, затраченное на последовательность расчёта: моделирование на «грубой» сетке, интерполяция на подробную сетку, моделирование на подробной сетке, более чем в полтора раза меньше времени моделирования непосредственно на подробной сетке с однородным потоком в качестве начального приближения, что оправдывает применение многостадийного процесса получения стационарного поля с использованием интерполяции.
Список литературы Интерполяция расчётных полей на многоблочных структурированных сетках для численного моделирования трёхмерного обтекания стреловидного крыла
- Горякин А.А., Новиков А.В. Интерполяция расчетных полей на многоблочных структурированных сетках для численного моделирования двухмерного обтекания угла сжатия // Ученые записки ЦАГИ. 2022. Т. 53, № 3. С. 29–38.
- Thompson J.F., Soni B.K., Weatherill N.P. Handbook of Grid Generation // CRC Press LLC. 1998. 1096 p.
- Jacquotte O.-P., Coussement G. Structured mesh adaptation: Space accuracy and interpolation methods // Computer methods in Applied Mathematics and Engineering. 1992. V. 101, N 1–3. P. 397–432.
- Tang T. Moving mesh methods for computational fluid dynamics // Contemp. Math. 2005. V. 383. P. 141–173.
- Егоров И.В., Новиков А.В., Федоров А.В. Прямое численное моделирование ламинарно-турбулентного перехода при гиперзвуковых скоростях потока на супер-ЭВМ // ЖВМиМФ. 2017. Т. 57, № 8. С. 1347–1373.
- Егоров И.В., Федоров А.В., Динь К.Х. Прямое численное моделирование ламинарнотурбулентного перехода при сверхзвуковом обтекании острой пластины // Ученые записки ЦАГИ. 2018. Т. 49, № 5. С. 17–25.
- Farin G. Curves and Surfaces for computer added geometric design: a practical guide, fifth edition // Morgan Kaufmann Publishers. 1999. P. 34—37, 245–247.
- Guttman A. R-trees: a dynamic index structure for spatial searching // ACM SIGMOD. 1984. V. 14, N 2. P. 47–57.
- Bayer R., McCreight E. Organization and Maintenance of Large Ordered Indexes // Acta Informatica. 1972. V. 1, N 3. P. 173–189.
- Cormen T., Leiserson C., Rivest R., Stein C. Introduction to Algorithms (Second ed.) // MIT Press and McGraw-Hill. 2001. P. 434–454.
- Knuth D. Sorting and Searching, The Art of Computer Programming, Volume 3 (Second ed.) // Addison-Wesley. 1998. V. 3. P. 481–491, 476–477.
- Go Programming Language [Электронный ресурс]. 2022. URL: https://go.dev/ (дата обр. 01.12.2022).
- CFD General Notation System [Электронный ресурс]. 2022. URL: http://cgns.org/ (дата обр. 01.12.2022).
- Tarantool platform [Электронный ресурс]. 2022. URL: https://www.tarantool.io/ (дата обр. 01.12.2022).


