Интерпретация математических моделей по данным микроволновой радиотермометрии

DOI:

В настоящее время в исследованиях искусственного интеллекта (ИИ) наблюдается значительный рост интереса к объяснимому искусственному интеллекту (eXplainable Artificial Intelligence, XAI) [27; 29]. Этот интерес обусловлен все более глубокой интеграцией ИИ-систем в различные сферы деятельности, где принимаемые решения оказывают критически важное влияние, например, в медицине, экономике, праве, а также в системах безопасности. В этих областях требуется не только высокая точность предсказаний, но и возможность объяснить, почему система приняла то или иное решение. Это необходимо для повышения доверия со стороны экспертов, принимающих решения, и пользователей, а также для обеспечения прозрачности работы алгоритмов и выявления потенциальных ошибок или предвзятости. Прозрачность работы моделей, в свою очередь, способствует их регулированию на соответствие нормам закона и этики, что позволяет внедрять системы ИИ в сферы деятельности с высоким уровнем контроля.

Сложность объяснимости моделей ИИ обусловлена тем, что современные алгоритмы машинного обучения, особенно нейронные сети, представляют собой комплексные нелинейные системы с большим числом параметров [10]. Такие модели зачастую функционируют как «черные ящики», в которых сложно понять внутреннюю логику принятия решений. Однако в области XAI принято выделять два уровня прозрачности моделей:

• •    Объяснимые модели [13] – представляют собой «черный ящик», где невозможно напрямую интерпретировать процесс принятия решений, однако существуют методы, позволяющие анализировать вклад признаков в итоговый результат. Примеры таких методов включают SHAP (SHapley Additive exPlanations [14]), Grad-CAM (Gradient-weighted Class Activation Mapping [33]) и LIME (Local Interpretable Model-agnostic Explanations [11]). Данные методы помогают выявлять, какие факторы наиболее сильно влияют на предсказания модели, что особенно полезно в медицинской диагностике и финансовом анализе.

• •    Интерпретируемые модели [30] – представляют собой «белый ящик», где процесс принятия решений полностью прозрачен и поддается анализу. К таким моделям относятся деревья решений, линейные модели, наивный байесовский классификатор и некоторые виды ансамблевых методов. Достоинство этих моделей заключается в простоте их интерпретации, что делает их востребованными в критически важных приложениях, таких как медицина, юридический анализ и оценка рисков.

Основным недостатком интерпретируемых моделей является их сравнительно более слабая предсказательная способность по сравнению с глубокими нейронными сетями. В свою очередь, последние демонстрируют высокую эффективность в широком спектре задач, таких как компьютерное зрение, обработка естественного языка и прогнозирование временных рядов [16; 17]. Таким образом, выбор между объяснимыми и интерпретируемыми моделями ИИ сводится к нахождению компромисса между точностью предсказаний и степенью прозрачности. В задачах, где ошибки не оказывают критического влияния, например, в рекомендательных системах, можно использовать нейронные сети без механизма объяснения решений. Однако во многих областях прозрачность играет ключевую роль, что делает оправданным применение менее точных, но более интерпретируемых моделей.

Основные направления исследований в области XAI на текущий день связаны с повышением прозрачности «черных ящиков», а именно нейронных сетей. Исследуются архитектуры, способствующие выделению интерпретируемых признаков и областей интереса, алгоритмы контекстного объяснения при работе с языковыми данными [20; 21; 26; 31]. Однако фундаментальная проблема нейронных сетей, заключенная в их непрозрачности, остается, из-за чего продолжают быть актуальными вопросы этики и безопасности в применении систем ИИ.

В данной работе предлагается модель, объединяющая преимущества обоих подходов, что позволяет одновременно достичь высокой точности и прозрачности системы ИИ. Известно, что объединение классических моделей машинного обучения (например, деревьев решений) в ансамбль может повысить общую точность предсказаний. Это достигается за счет того, что каждая модель ансамбля обучается на различных подмножествах признаков и данных, что обеспечивает их разнообразие. Высока вероятность, что среди ансамбля решений найдется модель, чьи предсказания будут схожи с результатами высокоточных нейронных сетей [9]. Включение интерпретируемых методов объяснения в такую систему позволяет не только повысить прозрачность работы алгоритма, но и обеспечить согласованность решений, что критически важно для практических приложений в ответственных сферах. Таким образом, рассматриваемый подход направлен на разработку гибридных решений, объединяющих возможности глубокого обучения и интерпретируемости традиционных методов.

Актуальной областью применения рекомендательных систем ИИ, особенно требующей прозрачности используемых моделей, является медицинская диагностика. Поскольку такие системы не несут ответственности за свои рекомендации, врачу необходимо не только получать предлагаемый вывод, но и понимать его предпосылки. В настоящее время системы ИИ активно разрабатываются совместно с методом микроволновой радиотермометрии [24]. Данный метод позволяет измерять глубинные температуры тела, на основе чего фиксируются температурные аномалии биологических тканей и органов, свидетельствующие о наличии различных заболеваний [6]. По измеренным температурам строятся модели машинного обучения, которые показывают свою точность при обследовании различных органов и заболеваний [4]. При этом для более эффективного применения систем были разработаны математические модели, формализующие знания врачей. Модели описывают характеристики температурных полей органов, на основе которых врачи определяют диагноз. Например, можно выделить характеристику, описывающую наличие области с повышенной температурой. Как правило, повышенная температура свидетельствует о воспалительных процессах, вызванных заболеванием.

Данные математические модели не только повышают точность машинного обучения, но и качество обоснования. Сложность обоснования напрямую зависит от информативности входных признаков: чем она меньше, тем в большей степени необходимо увеличение сложности моделей машинного обучения. Так, например, для сохранения точно- сти модели увеличивается глубина дерева решений при обработке большого количества малоинформативных признаков. И напротив, при использовании высокоинформативных признаков требуется меньшая глубина дерева решений. В данной работе рассматривается модель с использованием высокоинформативных признаков [5; 19] и их модификация для задач обоснования, а именно: модификация метода построения интервалов, а также дискретизация признаков на несколько категорий с учетом характерности для каждого из рассматриваемых классов.

Другим фактором, влияющим на качество систем ИИ, является качество обучающего набора данных [25]. А именно, его корректность и полнота, что зачастую слабо представлено в медицинских данных. Постановка корректного диагноза является нетривиальной задачей и медицинские наборы данных могут нести в себе нехарактерные метки, то есть такие, которые не свойственны измерениям. Полнота же может быть слабо представлена в силу малого объема данных, вследствие чего он является нерепрезентативным, что негативно влияет как на точность моделей машинного обучения, так и на адекватность обоснования, которое может делать акценты на второстепенных характеристиках. В работе рассматриваются подходы, корректирующие данные характеристики.

1.    Материалы и предшествующие результаты

В работе исследуется набор данных, полученных в результате обследований методом микроволновой радиотермометрии. В ходе обследований производилось измерение температур органа и тела по определенной схеме (см. рис. 1).

В каждой пронумерованной области измерялись глубинные и кожные температуры. Таким образом, набор данных по каждому пациенту содержит следующие температурные измерения:

• •    т r ^nw = (т' ш ^т^, ...,t ^m w ) — множество глубинных температур правой молочной железы;

• •    j m ^w _ (^ mw ,^ mw ,'"^ mw ) — множество глубинных температур левой молочной железы;

• •    Т" = (tQ _r ,t^ _r ,...,tg _r ) - множество кожных температур правой молочной железы;

• •    Т" = (t^^, t^,..., t^) — множество кожных температур левой молочной железы;

• •    J?™ = (t mW ,t ma ) - множество глубинных температур опорной области (точки Т 1 и Т 2 на схеме);

• •    Т" = (tl^t ^o ) - множество кожных температур опорной области.

По проведенным измерениям врачами осуществляется анализ температурных полей молочных желез (пример полей на рис. 2) на наличие и степень выраженности температурных отклонений от нормы. В результате анализа врач ставит в соответствие пациенту или молочным железам оценку – уровень выраженности температурных аномалий – по шкале от 0 до 5. Где 0 – температурные аномалии не выявлены; 5 – температурные аномалии характерны для рака молочной железы. Как правило, решается задача бинарной классификации, а именно определения группы риска, поэтому данные классы объединяются в два основных: метки 0, 1, 2 – в группу здоровых; 3, 4, 5 – в группу риска [1].

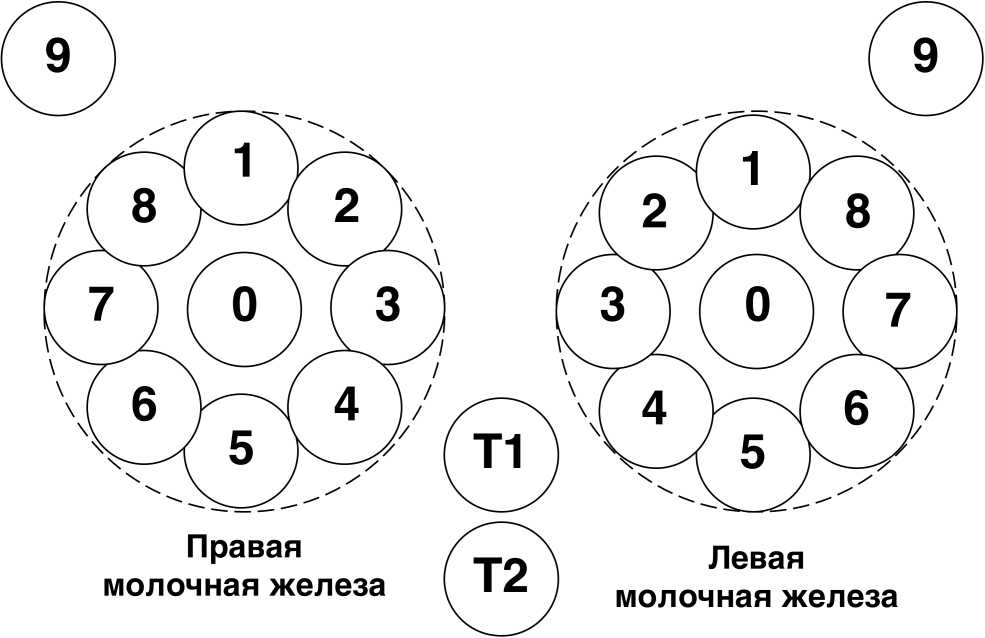
Рис. 1. Схема обследования. Здесь точки 0–8 – температуры молочной железы (правой или левой); 9 - аксиллярная область; Т 1 и Т 2 - опорные точки

В связи с тем, что в некоторых случаях врачи ставят метку пациентам, становится затруднительной задача определения состояния отдельной молочной железы, так как в таких случаях метка считается полуопределенной. Известно, что одна из молочных желез обладает характеристиками заданного класса, но неизвестно, какая из них. При этом исходя из предметной области полагается, что парная молочная железа не может принадлежать к более высокому классу, так как врачи ставят метку наивысшего класса уровня выраженности температурных аномалий. В таблице 1 представлен состав набора данных с известными и полуопределенными метками молочных желез.

Таблица 1

Состав набора данных

Класс	0	1	2	3	4	5
Количество объектов с известными метками	5 744	1 512	1 221	27	370	194
Количество объектов с полу-определенными метками	0	1 721	3 254	527	290	124

Ранее исследователями были построены математические модели диагностического состояния пациентов, количественно описывающие различные температурные аномалии органа. При этом было показано, что метод построения математической модели носит универсальный характер и применим к различным органам и заболеваниям (молочные железы и рак, нижние конечности и венозные заболевания, легкие и пневмония и т. д. [7; 18; 23]). В качестве примера элементов математических моделей выделим несколько:

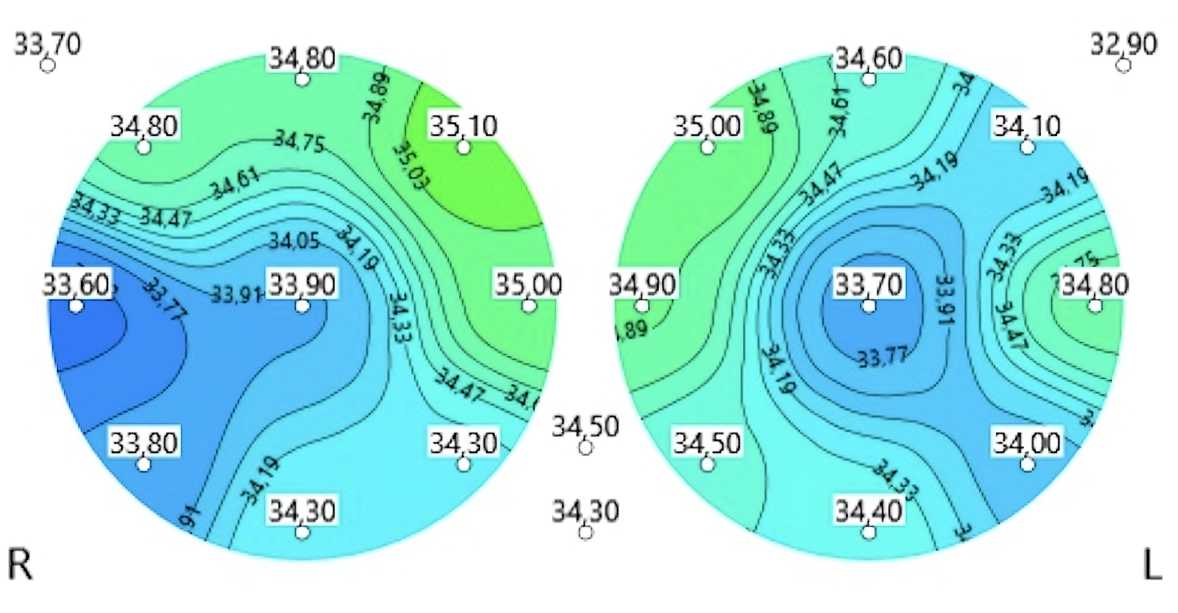
Рис. 2. Поле кожных температур молочных желез с отклонениями. Цвет соответствует значению температуры: синий – наиболее холодные области, зеленый – средние температуры молочной железы, красный – наиболее горячие области. Наличие синих областей и асимметрии полей правой и левой молочных желез может свидетельствовать о нарушении физиологических процессов

• •    Положение о симметрии температурных полей парных органов или систем. Наличие термоасимметрии свидетельствует о нарушении процессов в одном из органов. Симметрия может характеризоваться разностью средних значений глубинных тем-

• ператур

'T' mw г

-

m mw

1l

• •    Положение о наличии областей с повышенным уровнем температур, что, как правило, свидетельствует о воспалительных процессах в этой области. Наличие области может характеризоваться величиной разброса глубинных температур

  
  
2.    Интерпретация

V _m (t- Tmw 2 z_^ t e T^ \^b   r_r )

lT r ^nw | - 1

где | · | – мощность множества.

При этом элементами математической модели являются термометрические признаки: тройка значений ф = (f, I, Ж), где f - функция (например, разброс глубинных температур или разность средних значений, описанные ранее); I - интервал; Ж - информативность функции f на интервале I . Информативность характеризует то, насколько хорошо с помощью рассматриваемого интервала можно разделить объекты различных классов. На основе этого можно построить простой предикат, определяющий, входит ли значение функции f , полученное при данном обследовании, в интервал I . Если входит, значит значение характерно для мажоритарного класса в данном интервале. А на основе Ж возможно формирование математической модели, содержащей высокоинформативные термометрические признаки.

Использование термометрических признаков модели в задаче классификации позволяет повысить точность моделей машинного обучения, а также их интерпретируемость.

Основные критерии качества интерпретации математических моделей следующие.

• •    Понятность и простота интерпретации. Чем менее информативны признаки, используемые математической моделью, тем более объемной и сложной в понимании будет интерпретация. Несмотря на то что описанные математические модели повышают информативность входных признаков, актуальным остается разработка алгоритма нахождения интервалов, максимизирующих значение Ж, так как в работе [3] используется жадный алгоритм, который не всегда оптимален с точки зрения построения интервала для конкретного класса. Другим актуальным направлением является категоризация признака. Так как при бинаризации теряется большое количество информации, включающей в себя принадлежность к характерным значениям классов здоровых или группы риска.

• •    Интерпретируемость и точность. Модели машинного обучения, которые строятся по элементам математической модели, должны быть точными и в то же время интерпретируемыми.

• •    Адекватность. Адекватность характеризует, насколько решение и объяснение модели соответствует действительности. В первую очередь на адекватность влияет качество обучающего набора данных. А именно количество шумов (как в метках, так и в признаках), объем и репрезентативность данных. При слабой репрезентативности обучающего набора данных модели могут не учитывать некорректные закономерности или опираться на второстепенные факторы.

2.1.    Информативность термометрических признаков

Опишем алгоритм построения интервала I по признаку f для класса 0.

• 1)    На входе алгоритму поступают множества f ₀ и f 1 , содержащие значения функции f объектов класса 0 и 1 соответственно, а также указывается значение s - шаг расширения интервала.

• 2)    Левая (I i ) и правая (I _r ) границы интервала I определяются как медиана множества f o .

• 3)    Шаг расширения интервала вправо s _r принимается равным значению s.

• 4)    Пока s _r >  е, интервал I расширяется вправо на шаг s _r

  I r = I r + s

  
  

  r .

  
  

Если информативность W интервала (Il; Ir) меньше, чем информативность интервала (Il; Ir — sr), то возвращаются предыдущие границы интервала и шаг sr уменьшается вдвое

I r

I r

-

^s r

,

^S r

s _r

.

• 5)    Шаг расширения интервала влево s _l принимается равным значению s.

• 6)    Пока s _l >  е, интервал I расширяется влево на шаг s _l

^I i = ^I i ^{— s} i .

Если информативность Ж интервала (Ii; Ir) меньше, чем информативность интервала (Ii + sr, Ir), то возвращаются предыдущие границы интервала и шаг sl уменьшается вдвое si

J i — J i + ^s i , ^s i — 2 •

• 7)    В результате формируется интервал I — (Ir, I _r ).

Значение е является настраиваемым параметром, рекомендуемое значение - минимальное расстояние между элементами множества f ₀ U f 1

min | х — у | ,

^,y ^ f o ^ f i

Х=У так как при меньшем значении шага расширение интервала не всегда будет изменять соотношение количества элементов в нем.

В работе информативность W оценивается по формуле

^{W (} f^,I ) ^— фо • (1 ^— Ю, где

|{х С fn | Ii < х < Ir}| п —          Ifo Ufi| доля объектов класса п, попавших в интервал (Ii; Ir), характерный для данного класса.

Чтобы выявить эффективность данного метода, было проведено сравнение с методом жадного объединения [3]. В качестве признакового пространства были выбраны функции из работы [2, прил. A], интервалы строились для каждого класса (0, 1, ... 5) и проводилось сравнение средних информативностей по каждому из них. В таблице 2 представлены результаты. Как видно, в среднем описанный выше метод значительно повышает информативность признаков, хотя в частных случаях она может падать на 1–2 %.

Таблица 2

Информативность интервалов

Номер класса	IV по жадному алгоритму	IV по описанному алгоритму
0	0,56	0,60
1	0,38	0,51
2	0,41	0,48
3	0,49	0,64
4	0,36	0,59
5	0,41	0,61

3.    Интерпретируемость и точность

Сформулируем задачу гибридного обоснования следующим образом: имеются обученные на задачу классификации модели высокоточной нейронной сети и ансамбля интерпретируемых алгоритмов. Каждая из них определяется функцией классификации

С : R” Ч [0; 1], для объектов, описываемых п признаками. Пусть Спп - функция нейронной сети; Са - функция ансамбля алгоритмов. При этом последняя формируется на основе множества моделей ансамбля

Са = А(Са1,...,Сат}, где А - некоторая агрегирующая функция, принимающая итоговое решение о принадлежности объекта к какому-либо классу; Са1, ...,Сат - модели ансамбля. Так как нейронная сеть является более точной моделью, необходимо сформировать обоснование, наиболее согласованное с ней. Также для специалистов может иметь смысл формирование краевых обоснований, приводящих аргументы в пользу как предлагаемого класса, так и противоположных.

Для этого в данной работе предлагается следующий метод:

• 1)    Пусть для рассматриваемого объекта х определены С _а (х) и (С _{а 1} , ...,С _ат ).

• 2)    Определяется модель ансамбля со схожим решением

г = argmin(|Сnn(х) - Са^ |).(1)

j=1...m

И краевые случаи

«min = arg min Саj,(2)

j=1...m

«max = arg max Саj.(3)

j=1...m

• 3)    По определенным интерпретируемым моделям 1, 2, 3 формируется обоснование.

3.1.    Сравнение степеней уверенности

Опишем пункты 2 и 3 подробнее.

Ключевым элементом предлагаемого в работе подхода является сравнение выходных значений моделей классификации. В общем случае выходное значение С определяет степень уверенности классификатора в принадлежности объекта к заданному классу. Как правило, к классу с меткой 1. Зададим для этого степень уверенности следующим образом:

Y^{( x |} y) =

f С (х),

11 — С (х),

У = ¹

У = 0 ,

где х — признаковое описание объекта, у — класс. Здесь и далее рассматривается случай бинарной классифик;ции.

Если γ близка к 1, то это значение можно интерпретировать, как высокую уверенность модели в принадлежности объекта к классу у. Если же степень уверенности близка к 0,5, то объект является трудно определимым для модели и проявляет характеристики обоих классов.

Имея несколько моделей классификации, предполагается возможным сравнение их степеней уверенности в определении класса рассматриваемого объекта. Пусть Y nn -степень уверенности для модели нейронной сети, а

Y = {Y1, Y2,..., Ym}- степени уверенности для моделей ансамбля классификатора в принадлежности объекта к классу 1. Тогда наиболее согласованной моделью ансамбля будет та, степень уверенности которой ближе к Ynn i = arg min (|Ynn - ^|).

j = 1...m

На основе данного сравнения становится возможным выявление наиболее адекватного обоснования, если предполагать, что модель нейронной сети является наиболее точной.

Однако степени уверенности не всегда являются сопоставимыми из-за излишней уверенности ( overconfidence ) моделей [12]. Это явление, при котором значения Y почти всюду находятся в окрестностях чисел 0 или 1 (рис. 3).

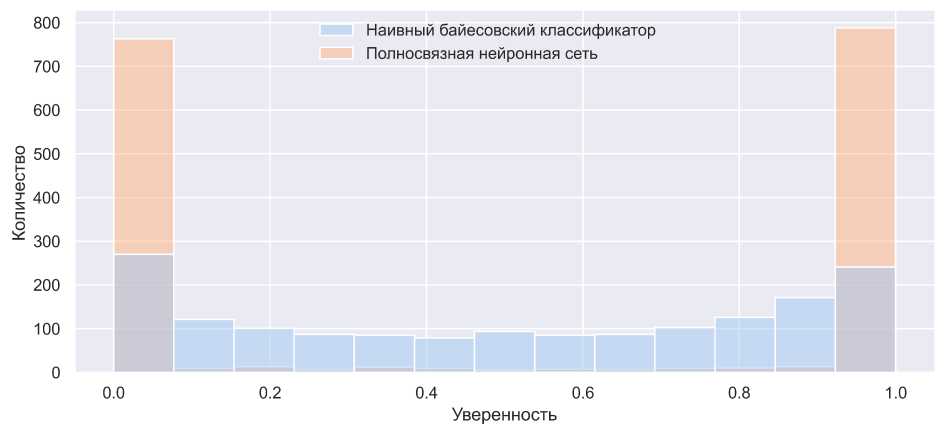
Рис. 3. Распределение параметра γ для наивного байесовского классификатора и полносвязной нейронной сети. Видно, что у байесовского классификатора более равномерное распределение по степени уверенности. Если применять формулу 4, то всегда будут выбираться такие же излишне уверенные модели. Модели обучались и тестировались на синтетическом наборе данных [32]

Чтобы модели были сравнимы, необходимо смягчить степень уверенности моделей, данный процесс называется калибровкой. Существует множество стратегий калибровки, приведем здесь лишь несколько [8; 22]:

• •    Логит-преобразование с уменьшением уверенности. Если функцией активации нейронной сети является сигмоида, можно применить логит-функцию для перевода вероятности в пространство логит-модели

^γ logit(Y) = ^log1 —_Y .

Затем применяется обратное преобразование, используя функцию сигмоиды с коэффициентом α, уменьшающим уверенность модели

Y ‘ = ^(a * logit(y)).

• •    Температурное сглаживание. Если функцией активации является функция softmax, аналогичным образом можно применить обратную функцию с коэффициентом α, сглаживающим распределение γ

‘ =      exp(Y(x, 1)/а)

E j е{ 0,1 } expM^j^{) /а )} ’

• •    Квантильное преобразование. Метод делит распределение величины γ на квантили и отображает их на интервал соответствующим заданному распределению образу. На рисунке 4(a) приведены сравнения данных методов, применяемых к распределению величины Y_nnиз рисунка 3. Подобные преобразования позволяют сделать результаты модели более адекватными. Так, ошибочные решения более близки к состоянию «неуверенности» (рис. 4(b)). Синим показаны значения уверенности модели нейронной сети на объектах, определяемых некорректно. Практически всегда модель присваивает им значение 0 или 1. После калибровки уверенность приближается к значению 0,5.

  

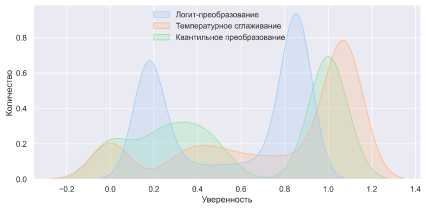
  (a) Распределения, полученные в результате калибровки описанными методами

  Рис. 4. Калибровка уверенности модели

  
  
  

  (b) Неуверенность модели

  
  
3.2.    Формирование обоснования на основе информативных областей

Формирование обоснования по выбранной интерпретируемой модели машинного обучения не представляет сложности из-за прозрачности механизмов принятия решений. Однако актуальным остается вопрос качества обоснования, а именно его простота и адекватность для конечного пользователя. В первую очередь обозначенные критерии зависят от формируемого признакового пространства. Чем полнее каждый из признаков описывает характеристические особенности классов, тем выше его информативность при обосновании.

Одним из подходов обоснования является сравнение значения признака объекта с нормой у объектов основного класса, то есть такого, от которого происходит отделение остальных [28]. В таком случае значения признака разбиваются на интервалы, определяющие степень отклонения признака от нормы (значение признака выше или ниже нормы, незначительно или значительно). В работах [5; 19] описан подход, который заключается в определении информативной области нормы. В данной работе предлагается подход, развивающий его за счет определения информативных областей обоих классов, в которых объекты в высокой степени отделимы от остальных.

Для этого определим высокоинформативный признак

F = (f,I,W), где f - функция; I = (11,12) - вектор информативных зон для каждого из классов; W -агрегированная информативность признака. В свою очередь, In - интервал, либо вектор интервалов, определяющих области характерных значений класса п (рис. 5). В рамках данной предметной области In - интервал.

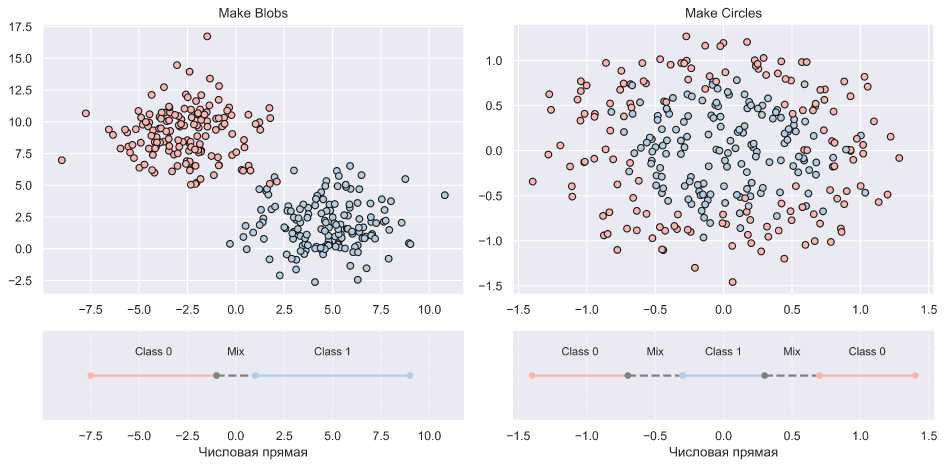
Рис. 5. Информативные зоны. Слева демонстируется пример, в котором по оси абсцисс каждый из классов характеризуется одним интервалом. Справа демонстируется пример, в котором объекты класса 0 характеризуются двумя интервалами. Наборы данных являются синтетическими [32]

На основе вектора I определим четыре области обоснования:

• 1)    I 12 - интервал, характерный для смешанных данных (пунктирная серая область на рисунке 5). Если в результате построения интервалы I 1 и I 2 пересекаются, то I 12 будет являться продуктом их пересечения

I12 = I1 И I2, а сами интервалы уменьшаются до границ пересечения

^I 1 = ^I 1 \ ^I 2 , ^I 2 = ^I 2 \ ^I 1 .

• 2)    I 1 - область, характерная для основного класса.

• 3)    I 2 - область, характерная для второго класса.

• 4)    Outlier = R\ [min(I ₁ , _l ,I ₂ ,_l ), max(I 1, _r ,I ₂ ,_r )] - области, определяющие нехарактерные данные, то есть выбросы. Здесь I _n,_l - левая граница интервала; I _n,_r - правая граница интервала.

Определим значения признака f *

• 0,f е к,

  f * = {

  
  
0.5, f е 1 12 , i,f е I 2 , 2, f е Outlier .

На основе данных категорий упрощается процесс обоснования. Так, зная, за какую из характеристик отвечает признак, возможно оценить степень характерности и его влияния на принимаемое решение. Если значение признака равно нулю или единице, признак влияет в высокой степени, если 0,5 или 2 – в меньшей из-за нехарактерности. Также такая категоризация признака повышает точность классификации относительно бинаризации. В таблице 3 представлены результаты бинарной классификации по бинарным термометрическим признакам и по категориальным. Результаты оценивались по трем метрикам:

• •    Специфичность – доля верноопределенных здоровых молочных желез.

• •    Чувствительность – доля верноопределенных молочных желез группы риска.

• •    Эффективность – среднегеометрическое из специфичности и чувствительности.

4.    Адекватность объяснения

Таблица 3

Результаты классификации

Признаки	Специфичность	Чувствительность	Эффективность
Бинарные	0,945	0,693	0,809
Категориальные	0,946	0,738	0,833

В настоящее время методы корректировки шумов в признаках широко исследованы, однако актуальной остается задача корректировки шумов в метках. При поиске ошибочных меток используются методы, определяющие степень характерности признакового описания объекта соответствующей метке [15]. Однако в них предлагается удаление объектов с нехарактерными метками, что негативно влияет на качество данных в условиях их малого объема. Поэтому для медицинских данных малого объема имеет смысл изменить метку на ту, чей класс наиболее характерен данному признаковому описанию. В качестве нахождения наиболее характерной метки можно использовать как многоклассовый классификатор, так и построенные интервалы. В интервалы какого класса объект чаще всего попадает, тому классу он и наиболее характерен. Такой подход позволяет не только исправлять нехарактерные метки, но и уточнять полуопределенные (см. табл. 1). Вычислительные эксперименты показали, что при уточнении полуопреде-ленных объектов с меткой 3 повышается точность его определения на тестовой выборке на 13 %.

Другой описанной проблемой данных малого объема является их слабая репрезентативность – степень, с которой обучающий набор данных отражает характеристики реального распределения объектов. Зная область характерных значений объектов по каждому признаку, возможно повышать репрезентативность данных, синтезируя объекты в них. Таким образом повышается качество обучающей выборки, что положительно влияет на адекватность математических моделей и их интерпретации.

Заключение

Рассмотренные в работе подходы демонстрируют повышение качества математических моделей и их интерпретации. Сравнение степеней уверенности позволяет выявлять наиболее согласованные с нейросетевыми предсказаниями решения деревьев решений, на основе которых осуществляется интерпретация результатов. При этом предложенный подход позволяет также регулировать степень и сложность интерпретации, привлекая большее количество моделей ансамбля, согласованных с нейронной сетью, или же, наоборот, наиболее несогласованные модели для приведения аргументов в пользу противоположного диагностического решения.

Категоризация термометрических признаков с выделением характерных зон для каждого класса позволила не только улучшить точность классификации, но и сделать интерпретацию более гибкой с определением пограничных случаев. Актуальным остается вопрос о категоризации признаков в многоклассовом случае, так как в таком случае возможно пересечение интервалов по нескольким классам, что приводит к снижению их информативности.

Предложенные методы построения информативных интервалов и корректировки обучающего набора на их основе позволяют повысить качество данных — как за счет устранения некорректных меток, так и за счет улучшения репрезентативности выборки. Это подтверждает значимость не только выбора модели, но и качества данных при построении систем объяснимого ИИ.