Интерпретация обратной задачи гравиметрии как задачи гравитационной томографии и внутривидения земли

На стыке геологии и математики получила большое развитие обратная задача гравиметрии [1, 2]. Ее суть заключается в следующем: используя измеренные на поверхности Земли аномалии потенциала или напряженности гравитационного поля (т. е. их отклонения от средних значений), нужно определить математическим путем аномалии плотности вещества под поверхностью Земли (в ее коре, мантии и т. д.) в некоторой пространственной области D .

Один из вариантов обратной задачи гравиметрии — задача интерпретации гравитационных данных [1–6]. Данная задача математически сводится к решению интегрального уравнения Фредгольма I-го рода или к минимизации функционала, равного сумме квадратов невязок между измеренными и вычисленными значениями потенциала (или напряженности) в ряде точек поверхности Земли. Это позволяет определить параметры месторождения (плотность, форму, размеры, массу, глубину залегания и т. д.) и по этим параметрам сделать его классификацию (нефть, руда и т. д.).

Обычно задача интерпретации гравитационных данных решается как набор двухмерных задач, а именно: в ряде вертикальных сечений определяются аномалии плотности, а затем составляется трехмерная (объемная) картина. Эта процедура весьма напоминает приемы, характерные для различных видов компьютерной томографии (КТ) [7– 9], в первую очередь для рентгеновской томографии (РТ) [7], [8, т. 1], [9, с. 17–33], [10] и МР-томографии [8, т. 2], [9, с. 33–62], [11–13]. Поэтому целесообразно относить обратную задачу гравиметрии и ее важный вариант — задачу интерпретации гравитационных данных к задачам томографии, как это уже сделано в работах [14, 15].

Более того, предлагается называть обратную задачу гравиметрии также задачей гравитационной томографии. Кроме того, особенностью данной задачи является то, что она позволяет без бурения скважин путем математической обработки поверхностных результатов "заглянуть" в глубь Земли, а это напоминает операцию внутривидения, характерную для МР-томографии [11, 12]. Поэтому предлагается называть обратную задачу гравиметрии также задачей внутривидения Земли [14, 15].

Предлагаемые толкования обратной задачи гравиметрии позволят воспользоваться обширными наработками в области компьютерной томографии, в особенности в РТ и МР-томографии.

МОДЕЛИ МЕСТОРОЖДЕНИЙ

И ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ГРАВИМЕТРИИ

Различные авторы вводят следующие модели месторождений [1, 4, 6, 16]: в виде четырехугольных усеченных пирамид, призм, цилиндров, брусов, многогранников, параллелепипедов, пересекающихся стержней и т. д. Однако такие фигуры обладают негладкими поверхностями и порождают громоздкие (хотя и несложные) формулы (см., например, [1, с. 90–105]). В работах [14, 15] предложено для моделирования месторождений использовать однородные (а также неоднородные) сфероиды . Данная работа продолжает эту тематику.

Решение обратной задачи гравиметрии, вообще говоря, не единственно [17]. В двухмерном (плоском) случае, согласно [5], решение задачи единственно (плотность р и область D тела однозначно восстанавливаются по внешнему полю), если кривая, ограничивающая D , есть лемниската, точнее овал Кассини [18, с. 125] — множество точек, для которых произведение расстояний до двух фокусов постоянно и равно некоторой величине d2 . А собственно лемниската — это овал Кассини при d = ∆ , где 2∆ — расстояние между фокусами. Уравнение овала Кассини в декартовых координатах имеет вид [18, с. 125]:

( x ² + y ²)² - 2 ∆ ²( x ² - y ²) = d ⁴ -∆ ⁴, d >  0, ∆ >  0.

При d > ∆ "4 2 овал является всюду выпуклым. Этому соответствует значение сферичности (отношение y -полуоси к x -полуоси) ε ∈ (1 / V3 ,1] , или ε ∈ (0.577, 1] . На рис. 1 приведены: овал Кассини (непрерывная кривая) и эллипс (пунктир) с одинаковым значением сферичности ε = 0.7 . Видим, что кривые весьма близки друг другу.

Однако овал Кассини обладает следующими недостатками: 1) он является выпуклым и поэтому удобным для моделирования лишь при ε ∈ (0.577,1] ; 2) нет теории гравитации овала, тем более его обобщения на трехмерный случай. Поэтому более целесообразно использовать для моделирования эллипс (и эллипсоид — его распространение на трехмерный случай), тем более что это удобная выпуклая фигура при ε ∈ [0, ∞ ) и имеются подробные разработки теории его гравитации ([19, 20] и др.). Что же касается неоднозначности решения при использовании эллипса (или эллипсоида), то для ее устранения нужно использовать ограничения на решение и метод регуляри-

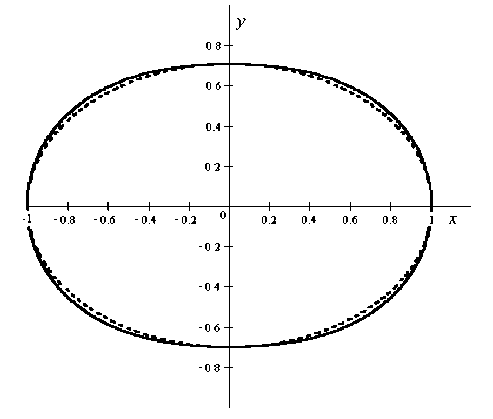
Рис. 1. Овал Кассини (сплошная линия) и эллипс (пунктир) с одинаковыми значениями сферичности ε = 0.7

зации Тихонова [14, 15]. Кроме того, для снижения многозначности гравитационных моделей целесообразно использовать дополнительно сейсмические данные [3, с. 22–28], [6, с. 31–34].

МОДЕЛИРОВАНИЕ МЕСТОРОЖДЕНИЯ СФЕРОИДОМ

Пусть некоторая область D под поверхностью Земли есть однородная среда с плотностью ρ ₀ = const , а месторождение (руда, нефть, интрузия, фундамент и т. д.) моделируется однородным сфероидом или несколькими сфероидами.

Напомним, э ллипсоидом называется тело, ограниченное поверхностью, уравнение которой ξ ² / a ² + η ² / b ² + ζ ² / c ² = 1 , где a , b , c — полуоси эллипсоида, а начало системы координат ξ , η , ζ расположено в центре тела. Если две из трех полуосей равны, то эллипсоид называется сфероидом (двухосным эллипсоидом, эллипсоидом вращения). Ниже приводятся практически удобные формулы для потенциала и компонент напряженности гравитационного поля сфероида на поверхности Земли.

ПОТЕНЦИАЛ И НАПРЯЖЕННОСТЬ СФЕРОИДА

Потенциал и напряженность сжатого сфероида

Рассмотрим сжатый сфероид , для которого a = b ≥ c . Поместим начало системы координат x , y , z в некоторую точку на поверхности Земли, причем ось z направим вниз. Пусть x , y ,0 — координаты гравиметра, а x ₀ , y ₀ , z ₀ — координаты центра сфероида (см. рис. 2). Исходя из работ [19, 20] в [14, 15] получены следующие формулы

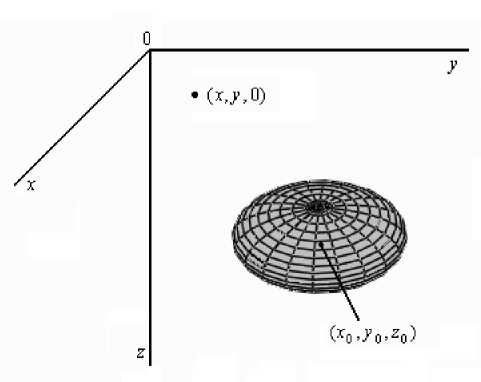
Рис. 2. Сжатый сфероид для потенциала V и компонент напряженности Vz, Vx и Vy в точке (x, y,0):

V ( X , У ,0) =

7 £

= 2 nYp a ² — e

arctg p -

⁽ x ^- x o ⁾² + ⁽ y - y o ⁾²

e ² a

x

сфероида, e = V1 - £2 — его эксцентриситет, p = q(4v, q = ea/r , r=7(x-x0)2Ky-y52^z02', v = 1 - q2 )+x(l - q2 )2 +(2 qz 0/ r)2

^v                      2^.

( x arctg p -

V

p 1

1 + p ²

r 7

2 z ₀ e ² a ²

( p - arctg p )

V z ( x , y ,0) = 4 ПР -у ( p - arctg p ) • z о , e ³

Потенциал и напряженность вытянутого сфероида

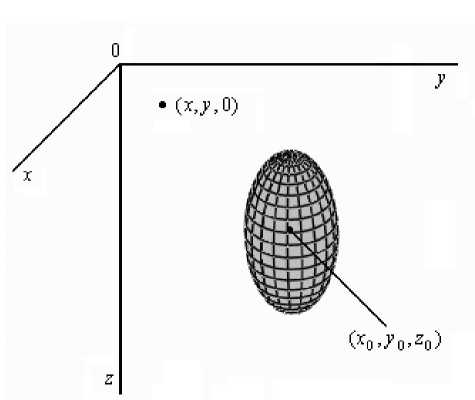
В случае вытянутого вдоль z сфероида , когда a = b <  c (см. рис. 3), получены следующие аналогичные формулы (также вне сфероида) [14, 15]:

V_x ( x , y ,0) =

£

= -2nyp — e3

arctg p

-

7 p

^ (1)

V ( x , У ,0) =

£

= 2 nypa —

e

-

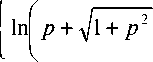
V

1 + p ²

• ⁽ x ^- x 0 ),

40Т Infp + 71 + p2)-,p e2 a2   V          7 TT+T2

V y ( x , y ,0) =

-

⁽ x ^- x 0 ⁾² + ⁽ y ^- y 0 ⁾²

£

= -2nyp — e3

\

arctg p

V

-

p

1 + p ²

r 7

• ⁽ У ^- У 0 ),

где у — гравитационная постоянная, p = const —

c плотность сфероида, £ = — < 1 — сферичность a

где

Рис. 3. Вытянутый сфероид

e ² a

x

x

p yl 1 + p ² - ln | p + д/ 1 + p²

V z ⁽ x , y ^,0) =

= 4nyp£ lnfp + V1 + p21" , p , e3 [ V 7 V1 + p

£

^V x ⁽ x , у ^,0) = ^{- 2 п}УР — ^x e ³

x

p >j 1 + p ² - ln [ p + ^/ 1 + p²

£

V y ( x , y ,0) = - 2 nyp — x

x

p si 1 + p ² - ln | p + ^/ 1 + p²

• z ₀ ,

• ^{( x - x} 0 ),

• ⁽ y ^- y 0 ),

^ (2)

£ = — > 1, e = si £2 -1, p = q(4t, q = eajr , a

r = V(x-x0)2 + (y-y0)2 + z02 ,

t ^+

+ 2 ( 1 - q ² ) 2 + 4 q ² [ ( x ^- x o ⁾² + ⁽ y ^- y о )² ] /r ².

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ СФЕРОИДА-МЕСТОРОЖДЕНИЯ ПО РЕЗУЛЬТАТАМ ГРАВИМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ

Рассмотрим данную задачу на примере измерения потенциала V ( x , y ,0). Пусть в ряде точек ( x i , y i ,0), i = 1,., n на поверхности Земли (в частности, на судне) измерены с помощью гравиметров значения потенциала ~ = ~( x i , y i ,0), i = 1,., n , где n — число точек измерения. Обозначим через V i = V ( x i , y i ,0), i = 1, .., n вычисленные согласно (1) или (2) значения V . Искомыми величинами являются следующие параметры сфероида (имитирующего месторождение): полуось в горизонтальной плоскости a = b , сферичность е , плотность р и координаты центра x ₀, y ₀, z ₀ — всего 6 искомых параметров.

Данная задача является некорректной и решается путем минимизации сглаживающего функционала Тихонова [21, с. 253]

n 6

£ (~ - V )² + а £ q j p²

i = 1                             j = 1

= min , a , е , р , x 0 , y 0 , z 0

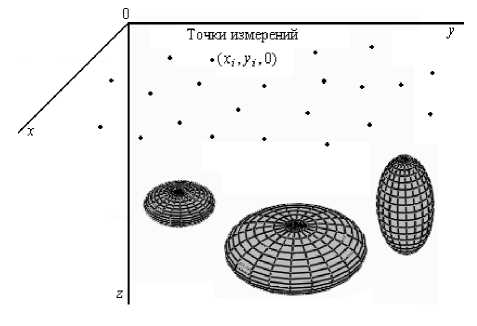
Рис. 4. Моделирование области месторождения несколькими сфероидами где P1 = a , p2 = E , p3 = р, p4 = x0 , p5 = y0 , p6 = z0, qj — веса, а > 0 — параметр регуляризации (обеспечивающий устойчивость решения). Для дополнительного повышения устойчивости и устранения неоднозначности решения следует использовать ограничения на решение: p j mm ^ p j ^ p j max , где p j mm , p j max Должны быть оценены заранее. В этом случае, например, qj = 1/ p2 max. Такая задача есть задача нелинейного программирования с регуляризацией [21, с. 253–255].

После отыскания a , е , р , x ₀, y ₀, z ₀ можно найти вертикальную полуось c = E a сфероида-месторождения, его объем v = (4/3) п a ² c , массу m = v р , глубину залегания h = z ₀ и т. д. Для более точного моделирования можно использовать несколько сфероидов (см. рис. 4).

ТИПИЧНЫЕ ХАРАКТЕРИСТИКИ ЗЕМНОЙ КОРЫ

Отметим некоторые типичные данные земной коры (подробнее см. в [1, 4, 6, 16] и др.).

Фоновая составляющая (гравитационный эффект от земной коры) [4, с. 335–340]: средняя плотность коры р ₀ = 2.67 г/см³, ее толщина d ~ 30 км, средняя сила тяжести g = V_z = 980 гал = 980 см/сек², а аномалии силы тяжести A g ~0.01 - 0.1 гал, т. е. на 4-5 порядков меньше g (и тем не менее такие аномалии надежно фиксируются гравиметрами).

Аномалии плотностей месторождений [4, с. 58–70]: верхнее рудное тело имеет аномалию плотности (отличие плотности от р ₀) А р = 1.6 г/см³, нижнее рудное тело имеет А р = = 0.8 г/см³, рыхлые отложения А р = 0.7 г/см³, вторичные кварциты А р = 0.05 г/см³ , руда мартитовая А р = 3.88 г/см³ , сланцы А р = 2.87 г/см³ и т. д. Видим, что аномалии плотностей А р могут быть сопоставимы со средней плотностью коры ^р 0 ^.

Типичная модель [16]: А р = 0.2 г/см³, глубина залегания 5 км, размер 2 X 2 км.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Разработан пакет программ IGP1 (Inverse Gravimetry Problem, ver. 1) на Fortran’е и MathCAD’е для моделирования прямых и обратных

O'

0 5 10 15 j 20 км

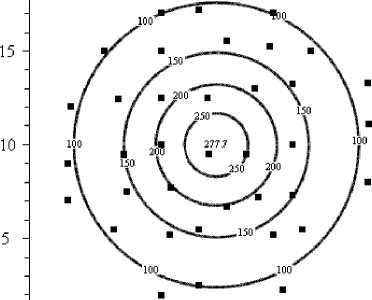
Рис. 5. Изолинии потенциала V ( x , y , 0) в см²/с² и точки его измерений на поверхности Земли

задач гравиметрии. Приведем результаты решения прямой задачи (расчет потенциала и напряженности по заданным параметрам месторождения) для следующего модельного примера , в котором месторождение моделируется одним сфероидом со следующими параметрами:

a = b = 1 км — большие полуоси сфероида в горизонтальной плоскости, е = c / a = 0.5 — его сферичность, р = 1 г/см3 — его плотность, x о = У о = 10 км, z о = 5 км — глубина его залегания.

На рис. 5–10 приведены результаты расчетов по формулам (1). На рис. 5 представлены изолинии гравитационного потенциала V ( x , y ,0) в см²/сек² и точки измерений потенциала на поверхности Земли. На рис. 6 — изолинии, а на рис. 7 — поверхность напряженности V_x ( x , y ,0) в см/сек². На рис. 8 — изолинии напряженности V_y ( x , y ,0) в см/сек². На рис. 9 — поверхность ^ V x² + V y² в см/сек². На рис. 10 — изолинии напряженности V_z ( x , y ,0) в см/сек². Видим, что картины гравитационных полей даже от одного сфероида могут быть довольно сложными.

Результаты решения обратной задачи будут опубликованы.

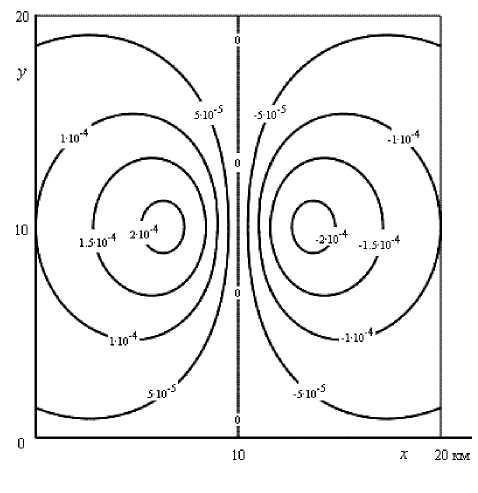
Рис. 6. Изолинии напряженности V x ( x , y , 0) в см/с²

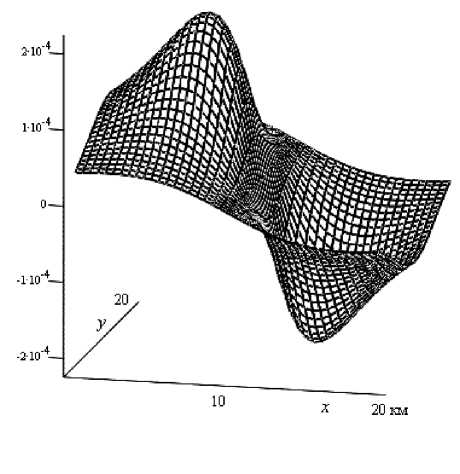
Рис. 7. Поверхности значений напряженности V_x ( x , y , 0) в см/с²

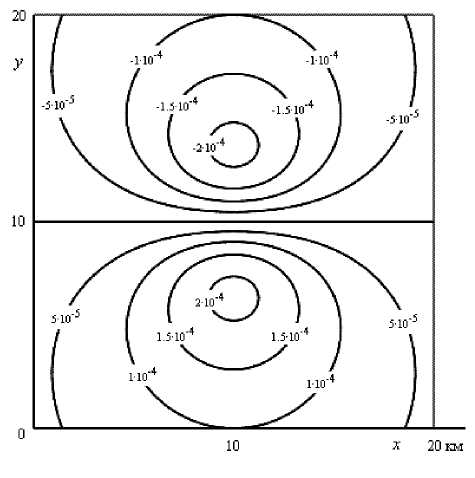
Рис. 8. Изолинии напряженности V_y ( x , y , 0) в см/c²

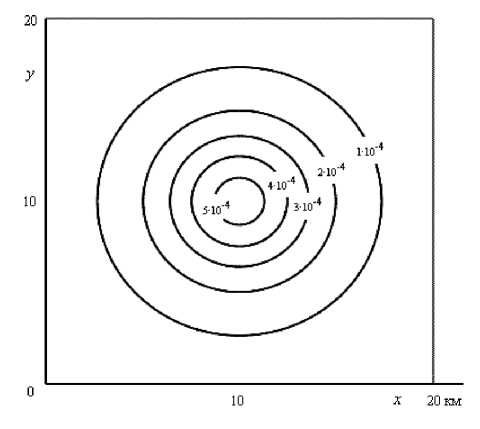
Рис. 10. Изолинии напряженности

V_z ( x , y , 0) в см/с²

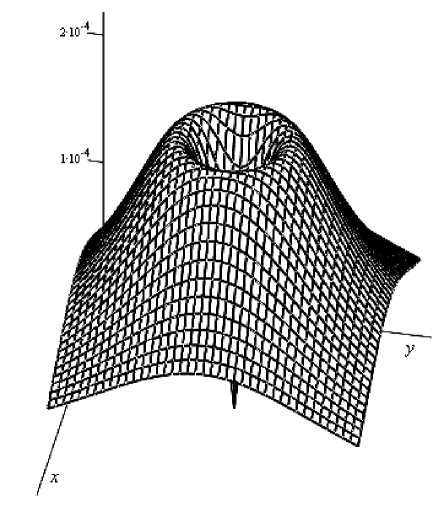
Р ис. 9. Пов ерхности значений

V ² + V ² в см/с² xy