Интерпретация трассерных исследований с помощью дискретной модели трещины

Трассерные (или индикаторные) исследования проводятся следующим образом: в нагнетательную скважину закачивается раствор специального вещества (трассер), затем производится отбор проб жидкости с добывающих скважин, и по результатам лабораторного анализа проб строятся графики зависимости концентрации трассера в отборах жидкости от времени. Совместное использование геолого-геофизических данных и результатов подобных экспериментов позволяет повысить достоверность знаний о строении нефтяной залежи и количественно оценить емкостные и фильтрационные параметры трещиноватых и пористых пластов [1, 2].

На практике к трассерному методу прибегают, как правило, для определения маршрута продвижения воды к скважинам с преждевременным обводнением продукции. Если это обводнение связанно с холостой циркуляцией нагнетаемой воды, то возникает необходимость в проведении мероприятий по изоляции высокопроницаемых каналов фильтрации в пласте [3]. Наиболее рентабельными являются технологии с закачкой водоизолирующих химических составов в водонасыщенные интервалы продуктивного

пласта [3]. Результаты интерпретации трассерных исследований выступают в качестве исходных данных при моделировании таких физико-химических способов увеличения нефтеотдачи. Кривые концентрации трассера в отборах жидкости с добывающих скважин, или кривые отклика, можно анализировать с трех различных точек зрения.

Во-первых, проводить качественную интерпретацию, то есть по кривым отклика определять наличие высокопроницаемых каналов и трещин между скважинами, связанность различных слоев между собой, направленность фильтрационных потоков в пласте. Кроме того, с помощью интегрирования кривой отклика по времени рассчитывается накопленный отбор трассера, который позволяет вычислить распределение объема нагнетаемой воды по соседним добывающим скважинам. С позиции этой точки зрения можно применять классическую методику количественной интерпретации [1, 2]. Согласно ей каждому пику кривой отклика с ( t ) соответствует канал с параметрами:

2 ц L ²

к = -------------- ,

( t 1 + t ₂ ^{) Д} p

( t\ + t ₇) t ²

V = Q-nj^M— ^C (t) Q (t) dt, total t где к — проницаемость канала; ц — вязкость жидкости; L — расстояние между скважинами; с (t) — кривая отклика (массовая концентрация трассера в отборе жидкости с добывающей скважины); t, и t2 — соответственно время начала и конца пика на кривой с (t); Дp — перепад давления между нагнетательной и добывающей скважинами; V — объем канала; Q — приемистость нагнетательной скважины; м ,„,„, — масса закачанного трассера; Q (t) — дебит добывающей скважины.

Во втором случае применяются более сложные математические модели, например, при генерации простейших аналитических кривых отклика и последующем их наложении на фактические кривые [4]. Сложные отклики при этом разбиваются на несколько простых аналитических откликов.

Наконец, с третьей точки зрения можно использовать численные симуляторы, базирующиеся на методе конечных объемов или методе трубок тока. Большинство коммерческих симуляторов позволяет учитывать наличие трассера в воде с различной степенью сложности [5].

Одним из недостатков классической методики [1, 2] является предположение о том, что каналы с низким фильтрационным сопротивлением (каналы НФС) изолированы от пласта. Таким образом, потери трассера из-за перетоков между каналами НФС и пластом не учитываются, что может привести к сильной недооценке объема такого канала [6].

В данной работе описывается способ интерпретации трассерных исследований, основанный на численном решении уравнения конвективного переноса трассера. Считается, что каналы НФС представляют собой дискретные вертикальные трещины, соединяющие забои добывающих и нагнетательных скважин. Предлагаемый подход лишен главного недостатка классической методики и дает более наглядное описание структуры межскважинного пространства, что упрощает последующее проведение численного моделирования процесса изоляции каналов НФС. По сравнению с коммерческими численными симуляторами применяется более простая гидродинамическая модель, позволяющая находить решение обратной задачи за приемлемое время (не более 5 секунд в экспериментах, представленных в данной статье). Отсутствие сжимаемости флюидов, многофазных, капиллярных и гравитационных эффектов в модели снижает уровень нелинейности обратной задачи и таким образом повышает устойчивость ее решения.

В Приложении к статье проанализировано влияние массообмена между дискретной трещиной и пластом на динамику прорыва воды по трещине к добывающей скважине .

2.    Предлагаемая математическая модель переноса трассера

При построении математической модели течения воды и переноса трассера в пласте и в трещинах принимаются следующие предположения:

• -    свойства пласта слабо меняются вдоль вертикальной оси;

• -    гравитационные эффекты отсутствуют;

• -    пласт плоский и двумерный;

• -    первоначально в пласте и трещинах содержится только чистая вода;

• -    вода несжимаема;

• -    трассер способен растворяться в воде;

• -    трассер полностью адсорбируется в пласте;

• -    трассер не адсорбируется в трещинах.

Предположение об адсорбции трассера в пласте вводится для того, чтобы кривая отклика всегда имела единственный пик, в противном случае часть трассера, движущаяся по пласту, будет образовывать второй пик, что усложнит процесс интерпретации.

Для описания течения воды и переноса трассера в пласте и в трещинах используются следующие

уравнения:

div u = 0, д C ф--- + div C u + qC 5  „ = 0, well д t k                                                            (3) u = - —grad p , ц q = lim J ( u , n 5(r) ) ds ■ S ( r )

Решение прямой задачи движения трассера заключается в отыскании при t >  о модельных кривых отклика — функций с ( t ) , в точках расположения добывающих скважин при следующих начальных и граничных условиях:

д р д п г

= 0,

Р ⁵ well = P bh ,

C ( t = 0 ) = 0,

C ( t )5  „

\  / well , inj

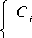
0,

t е ( 0, ',„] - tе (tnj, +”)■

Для учета адсорбции трассера в пласте вводится дополнительное условие:

C ( t I =⁰ .

В уравнениях (3)-(5) использованы следующие обозначения: u — вектор скорости фильтрации воды; ф — пористость породы; C и C — концентрация трассера во всей области (в пласте и в трещинах) и в нагнетаемой воде; t и t — текущее время и время закачки трассера; q — дебит (расход) воды; n — вектор нормали к s ( r ) (сфере радиуса r , локализованной в точке расположения скважины); п_г — вектор нормали к г , где г — внешняя граница пласта; 5^,, и s„_1Uinj — дельта-функции Дирака (их размерность 1/м³), локализованные, соответственно, в точках расположения добывающих и нагнетательных скважин и в точке расположения нагнетательной скважины, в которую производится закачка трассера; k — проницаемость породы; ц — вязкость воды; p и р_м — пластовое давление и фиксированное забойное давление скважины; п — область пласта с исключенными трещинами.

3.    Пространственная дискретизация

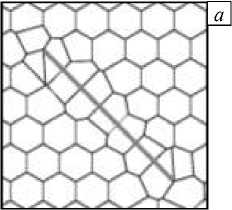
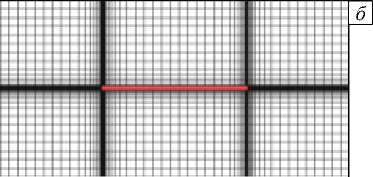
Для численного описания геометрии пласта и трещин применяется двумерная неструктурированная сетка Вороного [7] и дискретная модель трещины [8]. Трещины представляются в виде набора прямоугольных ячеек (Рис. 1 а ), ширина которых принимается равной ширине раскрытия трещины (от 0,001 мм до 10 см). Каждая ячейка трещины может быть соединена с подобной ей или с ячейкой пласта, благодаря чему учитываются перетоки воды из трещины в пласт и обратно (Рис. 1 б ).

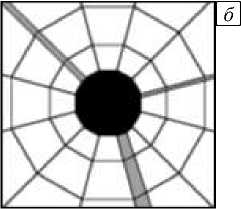
Для представления вертикальных скважин используется измельченная радиальная сетка, которая позволяет соединить забой скважины с произвольным количеством трещин (Рис. 2 а ). Забой скважины считается отдельной расчетной ячейкой (Рис. 2 б ), диаметр которой совпадает с диаметром ствола скважины (около 10 см), поэтому нет необходимости прибегать к аналитическим зависимостям для описания притока к скважине, таким, например, как формула Писмана [9].

Уравнения движения трассера решаются на этой сетке методом конечных объемов с помощью двухточечной аппроксимации потоков [10]. Расчетная сетка является ортогональной, поскольку в ячейках за узловые точки принимаются точки–генераторы диаграммы Вороного; это свойство увеличивает точность аппроксимации потоков между ячейками [7, 10].

а

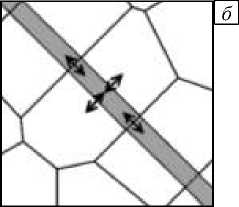
Рис. 1. Расчетная сетка для пласта с трещиной: ( а ) - сетка вокруг трещины, ( б) - увеличенное изображение сетки вблизи трещины (серым цветом обозначены ячейки трещины, черными стрелками - возможные направления течения воды между ячейками)

б

Рис. 2. Расчетная сетка для пласта с трещиной, проходящей между двумя скважинами: ( а ) - сетка вокруг трещины и скважин, ( б ) - схематическое изображение соединения забоя скважины с трещиной (серым цветом обозначены ячейки трещины, черным - ячейка забоя скважины)

4.    Верификация модели

Для верификации предложенной модели переноса трассера была рассмотрена прямоугольная область пласта с двумя скважинами, между которыми проходила трещина с проницаемостью 100 мкм² и шириной раскрытия 1 см (показана на рисунке 3 а ). Проницаемость пласта равнялась 0,05 мкм², толщина пласта — 10 м, расстояние между скважинами — 800 м, забойные давления скважин — 15 и 25 МПа. Аналогичная задача рассматривалась в коммерческом гидродинамическом симуляторе на декартовой расчетной сетке (Рис. 3 б ). При решении уравнений в обоих расчетах использовалась одинаковая величина временного шага — 10 часов. В нагнетательную скважину было закачано 10 м³ раствора трассера с концентрацией 30 кг/м³.

На рисунке 4 изображены кривые отклика, зарегистрированные на добывающей скважине. Максимальное абсолютное отклонение концентрации трассера составило 1,5%, а отклонение накопленной концентрации трассера — 0,15%. Таким образом, предложенную модель можно считать приемлемой для решения задачи переноса трассера.

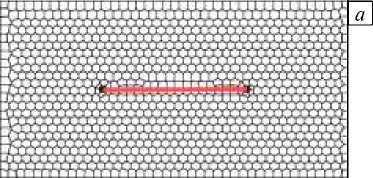
Рис. 3. Сетки для верификации модели переноса трассера в задаче с трещиной (показана горизонтальной линией), соединяющей две скважины: ( а ) - для расчета по предложенной модели, ( б ) - для расчета в коммерческом симуляторе (темные участки - места сгущения сетки)

Несмотря на то, что концентрация трассера в нагнетаемом растворе меняется скачкообразно, форма кривой отклика на рисунке 4 не имеет разрывов. Такое «размазывание» кривой отклика возникает по трем причинам: во-первых, скорость движения трассера в каждой точке трещины разная, поскольку трещина имеет конечную проводимость; во-вторых, происходит переток трассера из трещины в пласт; в-третьих, использованная расчетная схема обладает численной дисперсией. Первые две причины связаны с физикой процесса, а третья обусловлена вычислительными погрешностями; важная задача определения влияния каждой из них на вид кривой отклика остается открытой. В разделе 6 данной работы будет показано, что решение обратной задачи с помощью дискретной модели трещины довольно близко к решению, полученному с помощью классического метода интерпретации [1, 2], и, таким образом, в проведенных экспериментах численная дисперсия не оказывает существенного влияния на точность решения прямой и обратной задач.

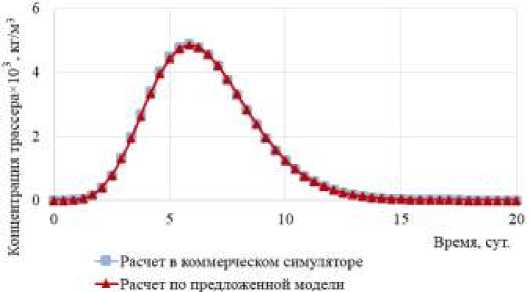
Рис. 4. Кривые отклика из расчетов по предложенной модели и с помощью коммерческого симулятора

5.    Решение обратной задачи

Интерпретация результатов трассерных исследований заключается в построении модели участка пласта и определении фильтрационных параметров этого участка с помощью решения обратной задачи. Предполагается, что трассер закачивается в одну нагнетательную скважину, а отбор проб производится на нескольких соседствующих с ней добывающих скважинах. Между нагнетательной скважиной и всеми взаимодействующими с ней добывающими скважинами проводятся трещины, вскрывающие всю толщину пласта. Для каждой добывающей скважины задана фактическая кривая отклика, и, таким образом, между трещинами и фактическими кривыми отклика устанавливается взаимно-однозначное соответствие. Каждая трещина характеризуется двумя параметрами: проницаемостью и шириной раскрытия. Обратная задача заключается в отыскании неизвестных параметров модели — векторов проницаемости k и ширины w — по имеющимся фактическим кривым отклика.

Обратные задачи такого рода могут оказаться некорректными. Для преодоления подобных затруднений в настоящее время разработано большое число регуляризирующих алгоритмов [11], с успехом применяющихся при контроле и управлении различными технологическими процессами. Все они основаны на том или ином способе учета априорной информации, позволяющей сузить область, в которой ищется решение обратной задачи. Априорная информация качественного характера, в предлагаемом здесь подходе — знание допустимых физических границ значений k и w — позволяет применить метод квазирешения [11]. За решение обратной задачи принимается вектор ( k , w ) , доставляющий минимум функционалу невязки

F ( k

w ) = « £

^ C ii, t, k , w dt । J sim ^{,   ,    ,}

t

J C fact ⁽ i , t ) dt

k t

।                 f argmax ( Csim (i, t, k , w ))

+ (i -O^i —t------------------- 1 | i | arg max ( C fact ( i, t ))

J                    k         t

a e ( 0,1 )

на множестве, которое может рассматриваться как класс корректности для данной задачи. Здесь: a — параметр; i — индекс добывающей скважины, для которой имеется фактическая кривая отклика; Cfact,' , t ) — фактическая кривая отклика i -й скважины; C_{si m}( i , t , k , w ) — модельная кривая отклика скважины i . По существу найденный вектор ( k , w ) будет являться квазирешением обратной задачи.

Проверка условной корректности постановки обратной задачи осуществлялась на трех наборах зашумленных синтетических кривых отклика, которые генерировались с помощью решения прямой задачи. В качестве шума использовался белый шум с нормальным распределением. Степень зашумленности кривой отклика вычислялась как относительное отклонение площади под графиком исходной и зашумленной кривых отклика, вычисленное в процентах. Минимизация целевой функции проводилась методом локальной оптимизации Нелдера–Мида [12].

На рисунке 5 показаны расчетная область пласта, расположение скважин и трещин. Рисунок 6 содержит синтетические кривые отклика с ненулевой степенью зашумленности и соответствующие решения обратной задачи. В таблице 1 приведены: исходные параметры трещин, на основе которых генерировались синтетические входные данные; параметры трещин, полученные в результате решения обратной задачи; использованные интервалы поиска параметров трещин и начальные приближения для этих параметров. Номера трещин совпадают с номерами добывающих скважин, с которыми они соединены.

Таблица 1. Параметры трещин, полученные в ходе проверки условной корректности обратной задачи

Номер трещины и исходные параметры трещин	Трещина №1, проницаемость, мкм2	Трещина №2, проницаемость, мкм2	Трещина №1, ширина, мм	Трещина №2, ширина, мм
Параметры	100	50	10	5
Интервал поиска	(0,1; 1000)	(0,1; 1000)	(0,01; 50)	(0,01; 50)
Начальное приближение для решения обратной задачи	500	500	25	25
Решение обратной задачи по синтетическим входным данным без наложения шума	100,14	50,23	9,97	4,95
Решение обратной задачи по зашумленным (1%) синтетическим входным данным	95,84	50,17	10,43	4,9
Решение обратной задачи по зашумленным (8%) синтетическим входным данным	94,9	37,2	10,08	6,29

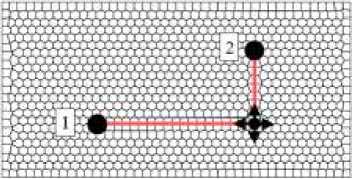
Рис. 5. Расчетная сетка для проверки условной корректности обратной задачи: цифрами указаны номера скважин, линиями обозначены трещины, черными точками – добывающие скважины, черной точкой со стрелками – нагнетательная скважина

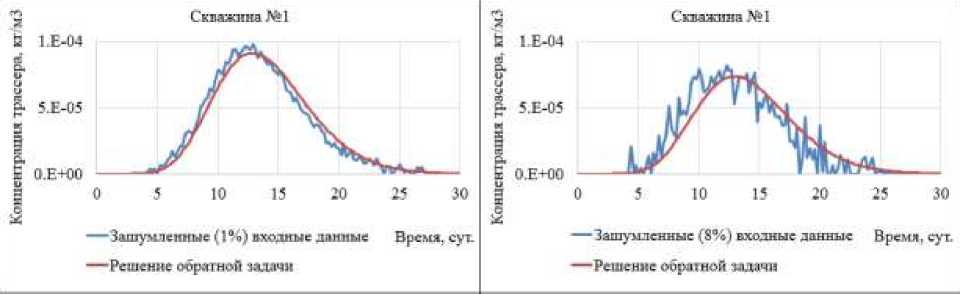
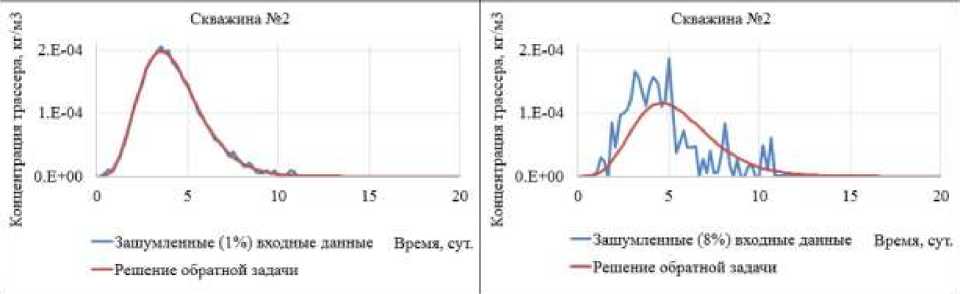
Рис. 6. Кривые отклика при проверке условной корректности обратной задачи

Из таблицы 1 видно:

– значения параметров трещин, полученные из решения обратной задачи по синтетическим входным данным без наложения шума, практически совпадают с исходными (отклонение не более 1%);

– отклонение вычисленных значений параметров трещин от исходных величин увеличивается с ростом степени зашумленности синтетических данных.

Таким образом, в данном эксперименте квазирешение обратной задачи существует и непрерывно зависит от входных данных. На единственность квазирешения указывает тот факт, что начальные приближения для параметров трещин находились на достаточно большом отдалении от исходных значений, а интервалы поиска параметров практически полностью охватывают допустимые физические границы соответствующих величин (Табл. 1).

6.    Сравнение предлагаемого и классического подходов

Для сравнения описанного и классического подходов проведена интерпретация трассерных исследований на опытном участке пласта, содержащем одну нагнетательную и три добывающих скважины

(Рис. 7). На рисунке 8 показаны модельные и фактические кривые отклика. Видно, что координаты вершин пиков и площади под графиками близки друг к другу.

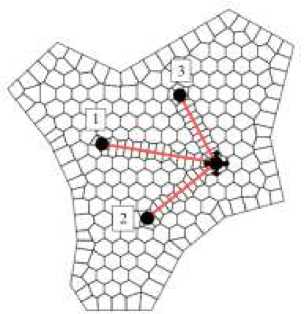
Рис. 7. Расчетная сетка и взаимное расположение скважин для расчета на опытном участке пласта; цифрами обозначены номера скважин, линиями – трещины, черными точками – добывающие скважины, черной точкой со стрелками – нагнетательная скважина

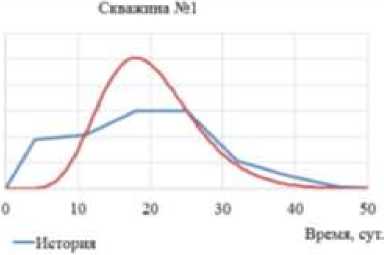
—Рсшсммс сора г Itoi шмж

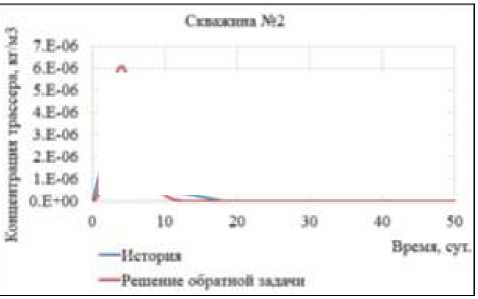
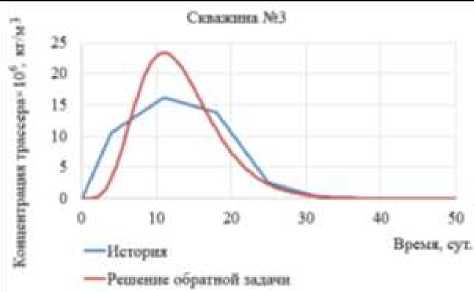
Рис. 8. Фактические и модельные кривые отклика на трех добывающих скважинах, полученные из расчета на опытном участке пласта

Таблица 2. Параметры каналов НФС, вычисленные с помощью классического метода [1, 2] по формулам (1) и (2)

Номер канала НФС	Проницаемость, мкм2	Объем, м3
1	4241	0,64
2	10573	0,03
3	3171	0,61

В таблице 2 приведены параметры каналов НФС, вычисленные на основе классического подхода к интерпретации [1, 2] по формулам (1) и (2). В таблицах 3, 4 представлены параметры трещин, вычисленные предложенным методом интерпретации. Объемы трещин в таблицах 3 и 4 вычислялись как произведение ширины раскрытия, длины и высоты трещины. Номера трещин и каналов НФС совпадают с номерами добывающих скважин, с которыми они соединены.

По данным таблицы 2 видно, что проницаемость канала №2 выше проницаемости двух других каналов. Это связано с тем, что пиковая концентрация трассера достигла добывающей скважины №2 раньше,

Таблица 3. Параметры трещин, вычисленные с помощью дискретной модели трещины (без перетоков между трещиной и пластом)

Номер трещины Проницаемость (мкм2) Ширина (мм) Объем (м3) 1 4060 0,019 0,27 2 10396 0,001 0,01 3 2973 0,031 0,29 чем двух других скважин (Рис. 8). Кроме того, канал №2 имеет относительно маленький объем (0,03 м3) из-за низкого значения накопленного отбора трассера на скважине №2, что хорошо просматривается на рисунке 8 (величина отбора пропорциональна площади под графиком кривой отклика).

Из таблиц 2 и 3 следует, что результаты классической интерпретации довольно близки к результатам интерпретации с помощью дискретной модели трещины без учета перетоков между трещиной и пластом: проницаемости отличаются не более чем на 5%, а объемы — на 50%. Ввиду радикального отличия использованных методов интерпретации отклонение в 50% можно считать допустимым. Описанное наблюдение указывает на то, что проведенные расчеты верны (в частности, численная дисперсия не оказывает существенного влияния на результат) и постановка обратной задачи корректна.

Сравнивания содержимое таблиц 3 и 4, можно заключить, что учет перетоков между трещиной и пластом сильно влияет на вычисленные объемы трещин — они возрастают не менее чем в 200 раз. Такое различие связано с тем, что существенная часть трассера по мере движения по трещине перетекает в пласт.

Таблица 4. Параметры трещин, вычисленные с помощью дискретной модели трещины (с перетоками между трещиной и пластом)

Номер трещины	Проницаемость (мкм2)	Ширина (мм)	Объем (м3)
1	7962	4,35	62,6
2	13960	1,92	21,0
3	4798	4,83	46,4

7.    Заключение

Предложен метод интерпретации трассерных исследований, основанный на представлении высокопроницаемых каналов фильтрации в виде дискретных трещин, соединяющих забои добывающих и нагнетательных скважин. Проведена верификация модели и построен устойчивый алгоритм решения обратной задачи. На примере с двумя трещинами показано, что квазирешение обратной задачи существует и непрерывно зависит от входных данных.

Показано, что при отсутствии перетоков между трещиной и пластом результаты интерпретации с помощью представленного метода близки к результатам классической интерпретации, а наличие перетоков увеличивает оцениваемый объем трещин в 200 и более раз. Последнее наблюдение согласуется с результатами, полученными в работе [6].

Установлено, что если в действительности добывающая и нагнетательная скважины соединены друг с другом некоторой сетью вертикальных трещин с проницаемыми стенками, то классический метод интерпретации может дать заниженную и неадекватную оценку объема этих трещин.

Сделанные выводы можно распространить и на случаи, когда высокопроницаемые каналы представляют собой горизонтальные пропластки с вертикальными перетоками. Хотя в горизонтальных пропластках линии тока трассера между скважинами будут иметь не линейный, а радиальный характер, специфика влияния перетоков на оцениваемый объем трещин останется прежней.

Работа выполнена при поддержке ООО «Уфимский НТЦ» и РФФИ (проект № 17-41-020226-р_а).