Interpretation of Normal and Pathological ECG Beats using Multiresolution Wavelet Analysis

Published Online December 2012 in MECS

The electrocardiogram, ECG, provides useful information about functioning of heart required for cardiovascular assessment. Basically ECG is a record of potential differences, measured at body surface, as electrical charges passes through atria and ventricles. Muscular contraction (systole) is associated with electrical changes known as depolarization The contraction of the atria manifests itself as the ‘P’ wave in the ECG and contraction of the ventricles produces the feature known as the ‘QRS’ complex. The subsequent return of the ventricular mass to a rest state, repolarization produces the ‘T’ wave. Repolarization of the atria is, however, hidden within the dominant QRS complex. The ECG signal provides the following information of a human heart:

• •    Heart position and its relative chamber size

• •    Impulse origin and propagation

• •    Heart rhythm and conduction disturbances

• •    Extent and location of myocardial ischemia

• •    Changes in electrolyte concentrations

• •    Drug effects on the heart

Therefore cardiac disorders can be correctly and timely identified based on the accuracy of detection of ECG wave components. Delineation means automatic detection of wave components along with positions, magnitudes and durations. Based on the accuracy of detection of above features, diagnosis of heart diseases can be correctly and timely done. The purpose of the work is to interpret normal and pathological ECG beats using multiresolution analysis.

There are several approaches available in literature for ECG interpretations with sensitivity above 99%. The worldwide popular, first of its kind, real time QRS detection based on slope amplitude and width was introduced by Pan and Tompkins [1]. Wavelet is a powerful tool for analyzing non stationary signal like ECG. Detection of characteristic points using continuous wavelet transform was proposed based on multiscale features [2]-[3]. Shubha Kadambe et al. compared the performance of dyadic wavelet transform based QRS detector with detectors based on Okada, Hamilton–Tompkins, and multiplication of the backward difference algorithms [4]. A review of all above seven types of algorithms along with the advantages was explained [5]. Hamde et al. described detection by multiresolution analysis which proved efficient feature extraction of ECG signals [6]. A precise approach was developed and evaluated by Martinez et al. using stationary wavelet transform [7]. The algorithm introduced various thresholds at wavelet subbands to detect QRS, RSR’, RS, QS patterns and to find onsets and offsets of P and T wave.

Zhao et al. [8] proposed a feature extraction method using wavelet transform and support vector machines and provided accuracy of 99.68%. Saurabh Pal and Mahmoodabadi et al. described procedure for selection of discrete wavelet coefficients correlated to P,QRS, T [9]-[10]. The automatic ECG signal analysis using wavelet packet transform (WPT) was presented by Wechit et al [11].

In the algorithm presented by Szi-wen Chen et al, filtering procedure based on moving averages to catch smooth spike-free ECG signal was explained [12]. An algorithm was presented by Chouhan and Mehta for detection of QRS, P, T based on the filter and modified slope [13]-[14]. A simple and reliable method termed as Difference Operation Method (DOM) to detect the QRS complex of an ECG signal was proposed [15]. The method was tested on arrhythmia database only.

The rest of this paper is organized as follows. Section II, describes the basics of ECG characteristic points by multiresolution wavelet analysis. The implementation of our approach on various normal and abnormal ECG signals with different sampling frequency is explained. Section III gives the results of our experimentation.

• II.    Material and Methodology
  
  2.1    Multiresolution analysis

Discrete wavelet transform represents a signal as addition of scaled and translated versions of scaling function ϕ(t) and scaled and translated versions of wavelet functions ψ (t). Multiresolution property means that the same wavelet function, ψ, can be represented by contracted versions of itself. The scaling function ϕ also possesses the same property since it is derived from wavelet function ψ. A wavelet ψ, an orthonormal basis for L ² (R), is expressed in terms of its dilated and translated family as

1 Z(t - nbam )

V m , n ⁽ t ) = -/^( t ) V —m—

J am     к a )

where the integers m and n control the wavelet dilation and translation respectively; a is a specified fixed dilation step parameter with a value greater than 1, and b is the location parameter which must be greater than zero. A preferred choice for discrete wavelet parameters a and b are 2 and 1 respectively. The power-of-two logarithmic scaling of both the dilation and translation steps is known as the dyadic grid arrangement. The dyadic grid is perhaps the simplest and most efficient discretization for practical purposes and lends itself to the construction of an orthonormal wavelet basis. Substituting a = 2 and b = 1 into equation (1), the dyadic grid wavelet can be written compactly as

• V , . ( t ) = 2 - m V ( 2 - mt - n )           _m

Discrete dyadic grid wavelets are usually orthonormal, i.e. they are both orthogonal to each other and are normalized to have unit energy. This is expressed as да

• J V m ', Д t ^V m , n ⁽ t ) = ^{1 if} m=m' and n=n' -да

=0 otherwise         (3)

This means that the information stored in a wavelet coefficient T m,n obtained from the wavelet transform is not repeated elsewhere and allows complete regeneration of original signal without redundancy. The corresponding family of orthonormal wavelets is an orthonormal basis. Using the dyadic grid wavelet of equation (2), the discrete wavelet transform (DWT) can be written as:

да

Tm, n = J x(t)vm,„ (t)dt

-”                                  (4)

where T m,n is known as the wavelet (or detail) coefficient at scale and location indices (m, n) . Orthonormal dyadic discrete wavelets are associated with scaling functions and their dilation equations. The scaling function is associated with smoothing of signal and expressed in terms of the original function ϕ, given by

• V m , n ( t ) = 2 - m ^/2 ^ (2 - m t - n )              ₍₅₎

where ф0,0(t) = ф(t) is sometimes referred to as the father scaling function or father wavelet The scaling function is orthogonal to translations of itself but not to the dilations of itself. The scaling function can be convolved with the signal to produce approximation coefficients as follows да

Sm,n = J x(t)Vm,n (t)dt

^-да                                            (6)

From the above, it is clear that the approximation coefficients are simply weighted averages of the continuous signal factored by 2m/2. The approximation coefficients at a specific scale m are collectively known as the discrete approximation of the signal at that scale. A continuous approximation of the signal at scale m can be generated by summing a sequence of scaling functions at this scale factored by the approximation coefficients as follows то xm (t) = E Sm,n (t^m,n (t) n=-то

Where xm(t) is a smooth, scaling-function-dependent version of the signal x(t) at scale index m. This continuous approximation approaches x(t) at small scales, i.e. as m→-∞. A signal x(t) can then be represented using a combined series expansion using approximation coefficients and wavelet (detail) coefficients as follows то                                    m 0 то

x (t) = y s (t)ф (t) +y у t (t~\щ (t)

m                 m,n       m,n                       m,n       m,n n =-то

m =-то n =-то

Therefore, from equation (8), the original continuous signal is expressed as a combination of an approximation of itself, at arbitrary scale index m0, added to a succession of signal details from scales m0 down to negative infinity. The signal detail at scale m is defined as то

dm (t) = E Tmn (t)V.„ (t) n=-то hence we can write equation (8) as m0

Xm (t) = Xrn n(t) +У dm (t)

m       m0           m m=-то

From this equation it is easy to show that addition of the signal details and approximation at an arbitrary scale can be obtained from signal approximation at a lower scale. This is called a multiresolution representation .

• 2.2    Normal and Pathological ECG

• 2.3    Algorithm Implementation

• 2.3.1    Pre-processing procedure:

• 2.3.2    Delineation procedure:

Abnormal heart conditions causes deviation in P Q R S and T wave parameters from normal values [18]. The accuracy in interpretation of interlead and intralead variability decides correct diagnosis. Table 1 shows list of variations in morphology.

Table 1: Characteristics of Pathological beats

Beat type	Change in Morphology
RBBB Right Bundle Branch Block	A terminal R wave in lead V1 QRS >0.10 sec QRS normal or deviated to the right Slurred S wave in leads I and V6,RSR’ pattern in lead V1 with R’ taller than R
LBBB Left Bundle Branch Block	QRS >0.10 sec QRS negative (QS or rS complex) in V1 and V2 QRS positive in V5 and V6 and often notched (RsR' wave) Absence of small normal Q waves in I aVL V5 and V6 Wide monophasic R waves in I aVL V1 V5 and V6
PVC Premature Ventricular Contraction	Irregular rhythm whenever PVC occurs. P Waves: and PR Interval not associated with PVC. QRS: Wide(>0.10sec) bizarre appearance
PAC Premature Atrial Contraction	Irregular rhythm whenever a PAC occurs P Waves: Present; may have a different shape PR Interval varies ; otherwise normal QRS: Normal
Fusion of normal with paced beats	TP segment is absent.
Left Ventricular Hypertrophy	R in lead I and S in lead III > 25mm R in AVL > 12 mm S> 25 mm in V1 R> 25 mm in V5
Myocardial Infarction	ST elevation or ST depression Pathological Q wave
Hypertrophy	Notch and enlarged P wave (Atrial Hypertrophy) Wide QRS complex (Ventricular Hypertrophy)

The R detection being prominent can be easily done on noise corrupted ECGs by our algorithm. However interpretation of P and T waves becomes difficult as these waves are obscured by presence of noise. Therefore preprocessing is prerequisite for precise detection of morphology. The first step of preprocessing prior to delineation is explained below.

Pre-processing basically consists of two steps: Dividing long term ECG into excerpts of 5 seconds duration and removal of noise and artifacts. During recording ECGs are inevitably contaminated by the different kind of noise and artifacts. For reduction of low and high frequency noise denoising steps are used proposed in earlier work [16].

Discrete wavelet transform observes the signal at different frequency resolutions and therefore is an appropriate choice for analysis of ECG signals. Fiducial points of ECG signal belong to different frequency bands and hence can be separated using multiresolution analysis. Choice of wavelet filter and depth of decomposition are important aspects in wavelet domain.

In the presented work, Daubechies 6 is selected being similar in shape to QRS complex and its energy spectrum is concentrated around low frequencies. The selection of depth of decomposition is normally done on the basis of spectral content of signal and sampling frequency. It is viable to select level of decomposition upto eight for all sampling frequencies. Table 2 displays bandwidths of detail coefficients and approximation coefficients for different sampling rates.

Table 2: Bandwidths of subbands for different sampling frequency (Fs in Hz)

Coefficients	Fs=128	Fs=250	Fs=360	Fs=500	Fs=1000
cD 1	[64, 128]	[125, 250]	[180, 360]	[250, 500]	[500, 1000]
cD 2	[32, 64]	[62.5, 125]	[90, 180]	[125, 250]	[250, 500]
cD 3	[16, 32]	[31.25, 62.5]	[45, 90]	[62.5, 125]	[125, 250]
cD 4	[8, 16]	[15.62, 31.25]	[22.5, 45]	[31.25, 62.5]	[62.5, 125]
cD 5	[4, 8]	[7.81, 15.62]	[11.25, 22.5]	[15.6, 31.25]	[31.25, 62.5]
cD 6	[2, 4]	[3.90, 7.81]	[5.62, 11.25]	[7.81, 15.62]	[15.62, 31.25]
cD 7	[1, 2]	[1.95, 3.90]	[2.81, 5.62]	[3.90, 7.81]	[7.812, 15.62]
cD 8	[0.5, 1]	[0.97, 1.95]	[1.40, 2.81]	[1.95, 3.90]	[3.90, 7.81]
cA8	[0, 0.5]	[0, 0.97]	[0, 1.40]	[0, 1.95]	[0, 3.90]

The bandwidth of ECG is usually stated as 0.5 to 100 Hz considering diversities. The Q, R, S, P and T peaks belongs to particular frequency band. Therefore these peaks can be extracted by preserving corresponding wavelet coefficients, in reconstructed signal.

Step1: R Detection :

Detection of R peaks is very important because correctness of all informative detections is dependent on these cardiac beats. In order to detect R peaks, the signal is reconstructed from detail coefficients of 3-5

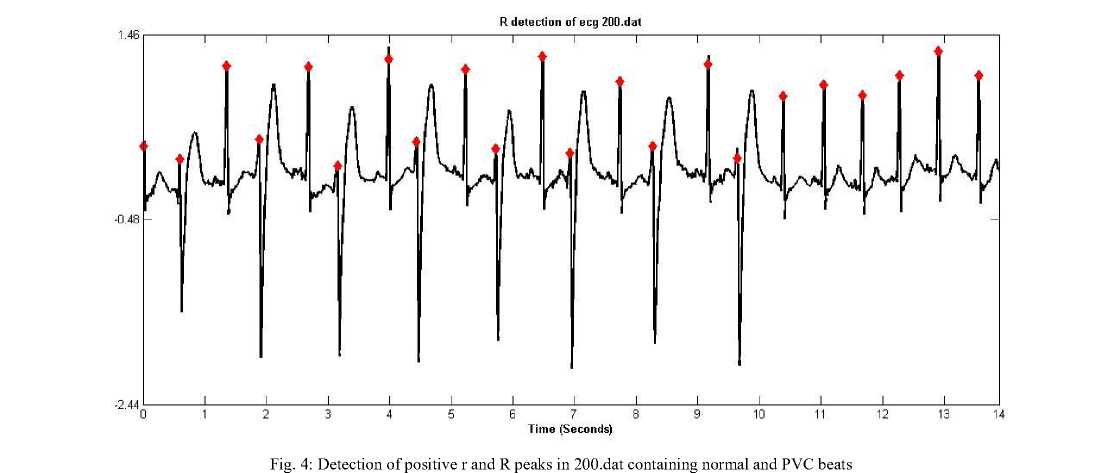
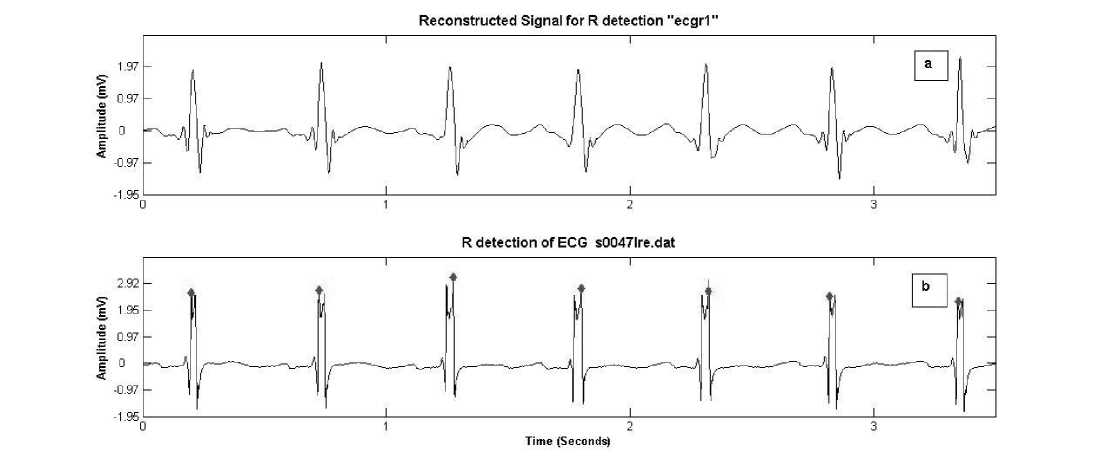
scales (cD 3 -cD 5 ) and setting rest of coefficients to zero. The signal contains frequencies from 31Hz to 125 Hz. The reconstructed signal “ecgr1” is thresholded where threshold T R equals RMS (cD 4 ). Differentiation of thresholded signal gives locations of positive and negative transitions (figure 1 (c)). Absolute maximum amplitudes of ecgr1 which exist within these locations are searched and positions ‘R_t’ are marked. The concerned amplitudes are recorded as ‘R_amp’ and denoted as R peaks in the original signal.

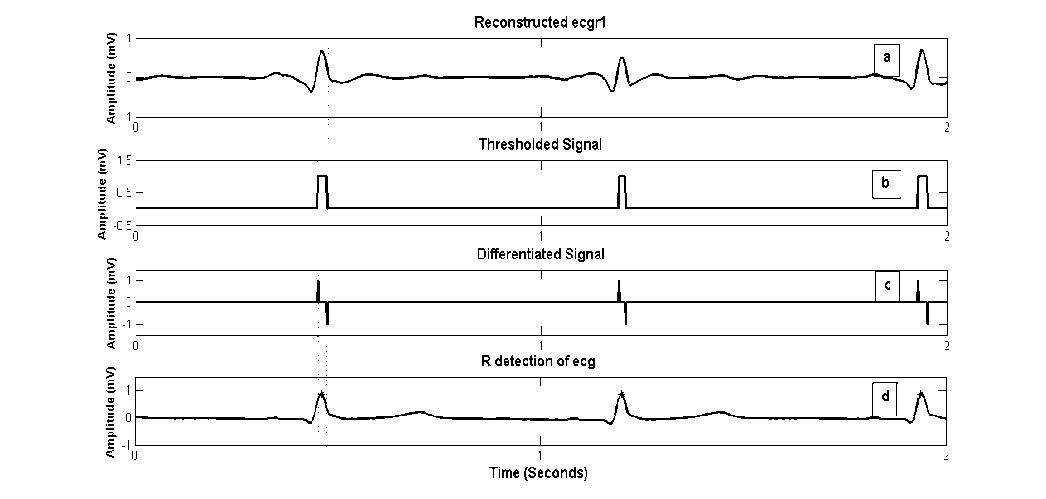
ECG databases available at physiobank have different sampling frequencies ranging from 128 Hz to 1 KHz [19]. Selection of subbands is highly dependent on sampling frequency. Interpretation of ECG records with sampling frequency 500 Hz is explained here. However for R detection on ECGs with various sampling frequencies, refer table 3 for selection of coefficients and threshold values.

Table 3: Selection of coefficients and thresholds for R detection

For R detection	Detail coefficients	Threshold
Fs=128	cD 1 , cD 2 , cD 3	RMS(cD 2 )
Fs=250	cD 2 , cD 3 , cD 4	RMS(cD 3 )
Fs=360	cD 3 , cD 4 , cD 5	RMS(cD 4 )
Fs=500	cD 3 , cD 4 , cD 5	RMS(cD 4 )
Fs=1000	cD 4 ,cD 5 , cD 6	RMS(cD 5 )

The algorithm considers all possible morphologies for R detection. The various configurations of QRS complex are QRS, QS, rSr’, RsR’, RS, rS, rSR’,QR, R. Fig. 2 and 3 shows examples of these complexes. The configuration of QRS complex is determined on the basis of following rules:

• •    R wave is always directed upward and has positive value.

• •    The magnitude of peak will declare ‘r’ or ‘R’. There is no golden rule for declaring ‘r’. If peak has amplitude greater than 0.25 mV then it is declared as R otherwise ‘r’.

• •    If R has succeeding R at a distance greater than 0.2 ms (0.2 ms is refractory period of heart) then it can belong to QRS, RS, QR or R complex.

• •    If small magnitude r is present then rSr’, rS pattern exist. Premature ventricular contraction (PVC) beats may contain r peaks.

• •    If R (or r) is followed by next immediate peak R’ (r’) with an intermediate value having opposite sign then RSR’ (rSr’) pattern is defined. The comparable middle value denotes a notch and R’ must be discarded.

• •    Premature ventricular contraction (PVC) beats may contain r peaks. Figure 2 and 3 shows detection of various configurations.

  
  
  
  
  
  
  

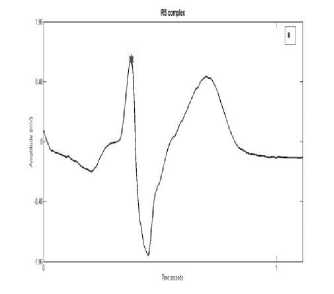
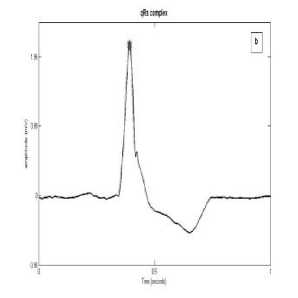
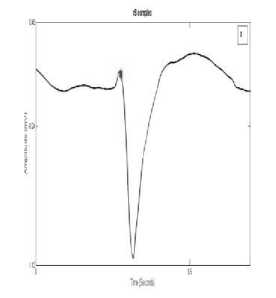
  Fig. 2: (c) rS complex

  
  

  Fig. 2: (a) RS complex

  
  

  Fig. 2: (b) R complex

  
  
  

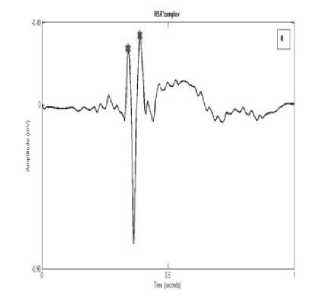
  Fig. 3: (a)rSr’ complex

  
  
  
  
  

  BSemplii

  

  П»|Ш««|

  
  

  Fig. 3: (b) QR complex

  
  

  Fig. 3: (c) QS complex

  
  

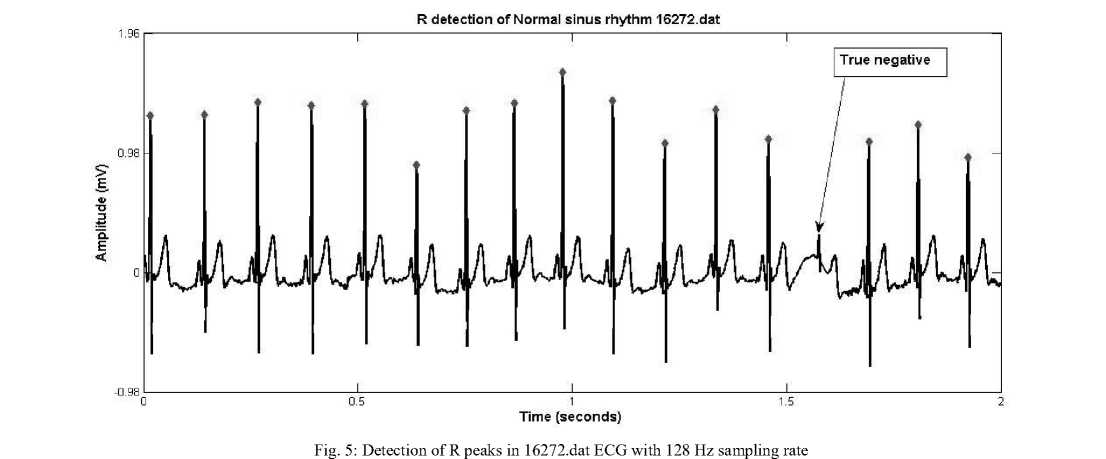
  The results of R peak detection on 200.dat from MIT BIH database (modified lead II, sampled at 360 Hz with 11 bit resolution) and on 16272.dat from Normal sinus

rhythm database of physionet (first lead, sampled at rate 128 Hz with 12 bit resolution) are shown in figure 4 and 5 respectively.

Step 2: Q and S peak Detection

Detail coefficients cD2–cD6 are used for reconstructing signal ecgr2. Normal QRS complex indicates that the electrical impulse has progressed normally from bundle of His to Purkinje network through the right and left bundle branches and that normal depolarization of the right and left ventricles has occurred. QRS interval can vary from 0.04 sec to 0.12 seconds, therefore the local minima Q and S peaks are searched about R_t values within 0.12 second window (60 samples for 500 Hz sampling rate) on reconstructed signal ecgr2 as shown in figure 6. The left location denotes Q_t he and right one denotes S_t . The corresponding magnitudes are noted as Q peak (Q_amp) and S peak (S_amp) .The following points are considered in Q and S detection step:

• •    Q and S detection is obtained by locating minima within fixed time interval (0.12 seconds) fails in case of pathological conditions. The QRS complex is wide and has duration greater than 0.12 milliseconds for paced beats, fused beats, premature ventricular   contraction.

Therefore search interval is safely increased to 0.16 ms considering 0.08*fs on both sides.

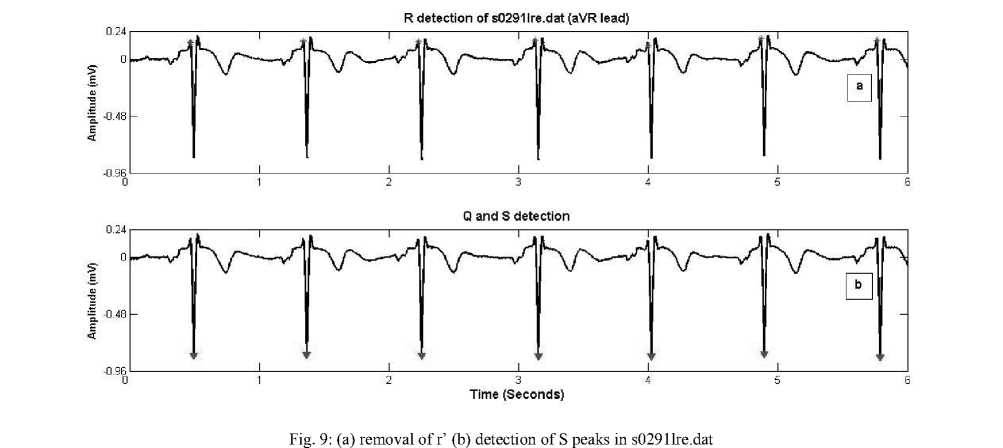
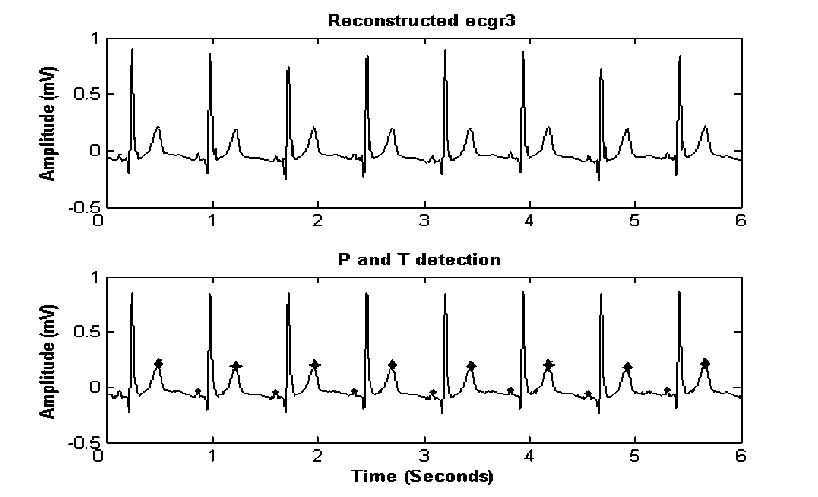
Fig. 10: (a) Reconstructed signal (b) Detection of positive T peaks in 11AL .dat

Step 3: P and T Wave Detection

T waves indicate repolarization of ventricles and T waves are normally asymmetrical, with first half having more gradual sloped than the second half. T waves are detected prior to P wave detection in this study. These waves are high-flying when only cD4-cD7 coefficients are kept for reconstructing signal ecgr3. The absolute maximum points of the signal, before Q and after S, are searched in ecgr3 signal. The magnitudes of P and T peaks are marked as P_amp and T_amp with their locations P_t and T_t respectively (figure 10). The details of P and T detection are as follows:

• •    For normal sinus rhythm QT interval may vary 0.34-0.44 seconds and never more than half of

interval between adjacent R waves. Therefore search window extends from first zero crossing position to 0.34 seconds from S location. For example S_t+(50 samples) to S_t+(170 samples) for sampling frequency 500 Hz. T wave, being dominant in this region, can be easily detected.

• •    PR interval may vary from 0.12 seconds to 0.20 seconds, so P wave is searched from first zero crossing point immediately before Q_t–(20 samples) to Q_t–(100 samples) for sampling frequency 500 Hz.

• •    The algorithm identifies three different morphologies of T wave positive, biphasic (+/-) and negative (in leads aVR, V1 may be in lead III) as shown in figure 10 and 11.

• •    The P wave morphologies considered are: positive, negative, biphasic P wave (mostly observed in lead V1), absence of P wave and P wave fused with T wave (figure 11).

• •    PVC beats arise from an irritable ventricular focus and therefore no P wave activity before QRS complex. Hence absence of P wave can be declared in a beat provided the interval between

R and preceding R is less than 0.8 seconds and wide QRS complex (as shown in figure 12).

Amplitude (mV)

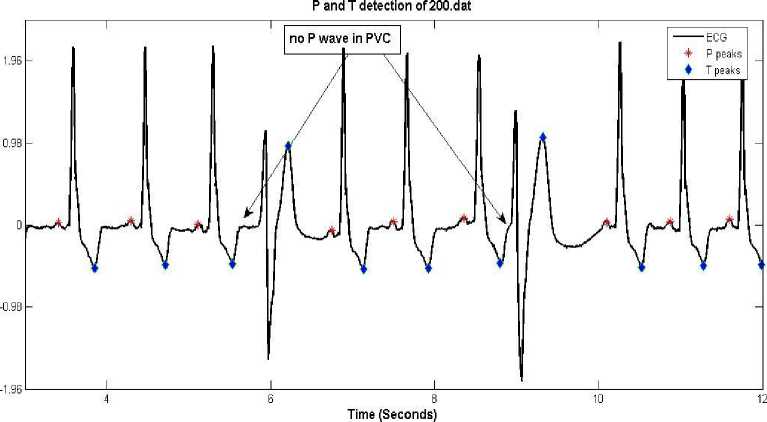
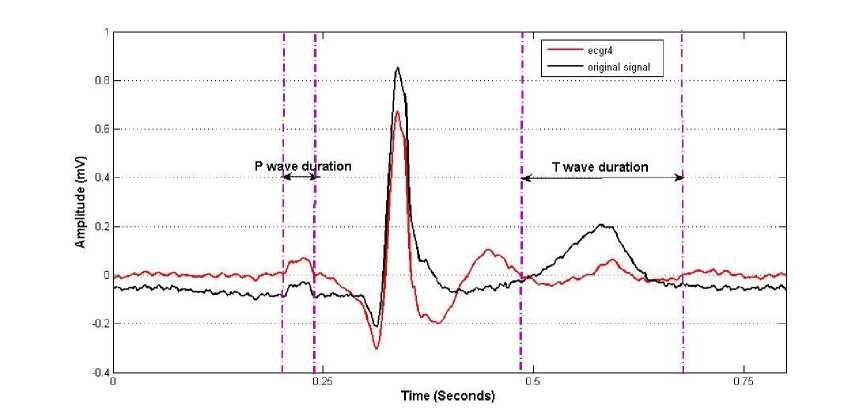
Fig. 13: Onset and Offset detection of P and T wave

• III. Results and Discussion

The algorithm was evaluated on records from physionet ECG databank and Glasgow Institute of cardiovascular and medical sciences. The algorithm was tested on multilead ECG signals with different sampling frequencies having interbeat and intrabeat variability. The steps in detection procedure are demonstrated on noise free 11AL.dat (from Glasgow database) in figures 3, 8, 12 and 15 respectively. The Glasgow database contains 15-lead (12 leads and three frank leads vx, vy, vz) normal ECG records each with 10 seconds duration. For verifying the performance of QRS detection process, manually annotated ECG records are essential. Therefore ECG records of Physikalisch-Technische Bundesanstalt diagnostic database (ptb-db) and MIT – BIH Arrythmia database and Normal Sinus Rhythm database were used for R peak detection.

The sensitivity Se and positive predictivity PP are the performance analysis metrics of QRS detection method and are expressed by the following equations:

Se = TP /(TP + FN )

PP = TP /(TP + FP )

where TP (true positives) denotes the number of R peaks correctly detected; FN (false negatives) represents the number of R peaks not detected (undetected) and FP (false positives) denotes the number of R peaks detected erroneously (misdetected). Table 4 denotes performance metrics of our proposed algorithm.

Sensitivity of most of ECG records was found to be 100%. The challenging ECG records characterized by high complexity and with noise content, (105, 108, 200 and 203 of MIT BIH database) brought it down to 99.18 %. The proposed method has provided less Se and PP by detecting more number of the FN and FP in 108.dat QRS complexes. The 108.dat has p waves closely resembling R waves and therefore ambiguously detected. These are removed on the basis of slope threshold.

The notches present in the QRS complex are removed because of proper coefficients selection to reconstruct ecgr1 as shown in figure 14.

Table 4: Performance of R Detection algorithm on MIT – BIH Arrythmia records

Patient ID	Total beats	Detected Beats	TP	FN	FP	Se %	PP %
100	2273	2273	2273	0	0	100	100
101	1863	1868	1861	2	7	99.89	99.63
103	2084	2084	2084	0	0	100	100
102	2188	2188	2187	1	1	99.95	99.95
104	2211	2223	2207	4	18	99.8	99.19
105	2567	2574	2558	9	16	99.65	99.38
106	2027	2048	2020	7	28	99.6	98.63
107	2137	2141	2137	0	4	100	99.81
108	1756	1830	1740	16	90	99.0	95.
200	2603	2613	2603	0	10	100	99.63
203	2431	2332	2303	101	29	94.73	98.76
205	2162	2173	2162	11	1	99.49	99.95
208	2404	2396	2324	80	42	96.67	96.99
209	2440	2438	2438	2	0	99.92	100
210	2142	2105	2100	41	5	98.23	99.71
212	2240	2240	2240	0	0	100	100
213	2635	2634	2634	1	0	99.96	100
215	2718	2708	2708	10	0	99.6	100

of ecg detection detection

0.8

0.5

0.1

-0.3 0

0.8

0.5

0.1

-0.2 0

0.8

0.5

0.1

-0.3 0

R Detection

Q and S

P and T

Time (Se

IN3034

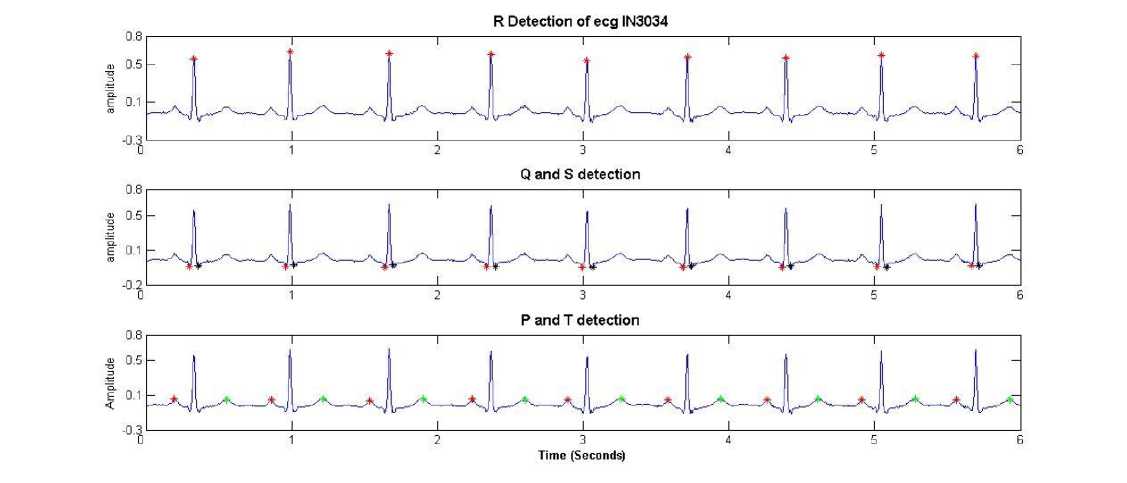
Fig. 15: Fiducial points detection on healthy Indian ECG record In3034

The algorithm was tested on various records from Indian database Center at S.G.G.S. Institute of Engineering and Technology, Nanded. Figure 15 shows fiducial point detection of In3034 record with sampling rate 500 and 12 bit resolution.

R peak detection worked successfully on normal QRS as well as on different morphologies. The viability of our procedure was verified on various morphologies for pathological conditions like Left Bundle Branch Block (LBBB), Right Bundle Branch Block (RBBB),

Premature Ventricular Contraction (PVC), Atrial premature beats, Supraventricular beats, first degree AV block, Fusion of normal beats with paced beats, Myocardial Infarction (MI), Hypertrophy .Table 5 indicates the mean values of QRS duration QT interval and RR interval for ECGs with different morphology. Table 6 shows performance of proposed algorithm on various databases.

Table 5: Mean values of features for pathological beats

Patient ID	Beats category	Lead Number	QRS duration S_t- Q_t	QT inter val Toffset- Q_t	R-R interval R-t – R-t
111.dat	LBBB	ML II	0.12	0.43	0.84
118.dat	RBBB	ML II	0.10	0.59	1.2
214.dat	PVC	ML II	0.15	0.50	0.54
200.dat	APC	ML II	0.10	0.44	0.52
s0080lre.dat	MI	V1	0.09	0.20	0.72
S0432_re.dat	Hypertrophy	Lead I	0.08	0.5	0.88
11AL.dat	Normal	aVL	0.09	0.36	0.74

	Table 6: Performance on various databases
	Database	Specifications	Detected Beats	Se (%)	PP (%)
	MIT-BIH database	360 Hz,2 channel, 11 bit resolution over 10 mV	50838	99.5	99
	MIT- BIH Normal Sinus Rhythm Database	128 Hz, 2 channel, 11 bit resolution over 10 mV	27123	99.8	100
	PTB Diagnostic Database	1 KHz, 15 channel, 16 bit, resolution over 32 mV	9061	99.5	99.8
	Glasgow database	500 Hz,15 channel, 12 bit over 2 mV	4200	100	100
IV. Conclusion                                         References

Choice of proper coefficients in multiresolution wavelet analysis delineates wave components of ECG. Interpretation of morphologies on 12 lead ECG signals for different sampling frequency was tested. The study proposed various decision rules to the existing selective coefficient method to detect different pathological conditions. The algorithm worked successfully on different pathological conditions and offered good sensitivity and positive predictivity. Denoising is prerequisite for accurate detection of ECG signals. To identify atrial and ventricular flutter beats energy content of subbands should be monitored. Accuracy can be enhanced at the cost of computational burden.

The work was supported by funds from All India Council for Technical Education (AICTE), New Delhi under Research Promotion Scheme Grant No 8023/RID/RPS-86/2011-12. We thank Prof. Peter W. MacFarlane of University of Glasgow, Scotland for providing ECG database for our research work.

• [1]    Jiapu Pan and Wiilis, Tompkins, A Real Time QRS Detection [J]. IEEE Transactions on Biomedical Engineering, 1985:230-238.

• [2]    V. Di Virgilio, C. Francalancia, S. Lino, S. Cerutti, ECG Fiducial Points Detection through Wavelet Transform [C]. IEEE-EMBC and CMBEC, 1995:1050-1052.

• [3]    Cuiwei Li, Chongxun Zheng, and Changfeng Tai, Detection of ECG Characteristic Points using Wavelet Transforms [J]. IEEE Transactions on Biomedical Engineering, 1995, 42: 21-28.

• [4]    Shubha Kadambe, Robin Murray and G. Faye Boudreaux-Bartels, Wavelet Transform based QRS Complex Detector [J]. IEEETransactions on Biomedical Engineering, 1999, 46.

• [5]    Bert-Uwe Köhler, Carsten Hennig,Reinhold Orglmeister, The Principles of Software QRS Detection Reviewing and Comparing Algorithms for Detecting ECG Waveform [J]. IEEE Engineering In Medicine And Biology, 2002:42-57.

• [6]    S. C. Saxena, V. Kumar, and S. T. Hamde, Feature extraction from ECG signals using wavelet transforms for disease diagnostics [J]. International Journal of Systems Science, 2002, 33: 1073-1085.

• [7]    Juan Pablo Martínez, Rute Almeida, Salvador Olmos, Ana Paula Rocha, and Pablo Laguna, A Wavelet-Based ECG Delineator: Evaluation on Standard Databases [J]. IEEE Transactions on Biomedical Engineering, 2004, 51:570-581.

• [8]    Qibin Zhao, Liqing Zhan, ECG Feature Extraction and Classification Using Wavelet Transform and Support Vector Machines [C]. International Conference on Neural Networks and Brain, ICNN&B, 2005, 2: 1089-1092.

• [9]    S. Z. Mahmoodabadi, A. Ahmadian, and M. D. Abolhasani, ECG Feature Extraction using Daubechies Wavelets [C]. Proceedings of the fifth IASTED International conference on Visualization, Imaging and Image Processing, 2005: 343-348,

• [10]    Saurabh Pal, Madhuchhanda Mitra, Detection of ECG characteristic points using Multiresolution Wavelet Analysis based Selective Coefficient Method [J]. Measurement, 2010, 43: 255-261.

• [11]    Wechit Kusathitsiriphan, Surapun Yimman, Chaiyan Suwancheewasiri and Kobchai Dejhan , Automatic EGG Characteristic Analysis using Wavelet Packet Transform, ISCIT, 2006:11531157.

• [12]    Szi-Wen Chen, Hsiao-Chen Chen, Hsiao-Lung Chan, A real-time QRS detection method based on Moving-Averaging Incorporating With Wavelet Denoising [J]. Computer Methods and Programs in Biomedicine, 2006, 82:187–195.

• [13]    V. S. Chouhan, and S. S. Mehta, Detection of QRS Complexes in 12 lead ECG using Adaptive Quantized Threshold [J]. International Journal of Computer Science and Network Security, 2008, 8: 155-161.

• [14]    V. S. Chouhan, and S. S. Mehta, Threshold-based Detection of P and T-wave in ECG using New Feature Signal [J] International Journal of Computer Science and Network Security, 2008,8 :144-152.

• [15]    Yun-Chi Yeh, Wen-June Wang, QRS complexes detection for ECG signal:  The Difference

  Operation Method [J]. Computer Methods and Programs in Biomedicine, 2008, 91:245–254.

Shubhada Ardhapurkar She received Master of Engineering degree in 1994 She is currently pursuing Ph.D. in Biomedical Signal Processing Techniques from S.G.G.S. Institute of Engineering and Technology, Nanded, Maharashtra, India. Her interests include signal processing, VLSI, Communication and neural networks.

Ramchandra Manthalkar He received Ph.D. degree from Indian Institute of Technology, Kharagpur in Image Processing in 2003 and is currently working as Professor and Head in Electronics and Telecommunication Engineering Department at S.G.G.S. Institute of Engineering and Technology, Nanded. He has published more than 15 research papers in peer reviewed Journals and Conferences. He is currently guiding 6 research scholars for their Ph.D. work. Dr.Ramchandra Manthalkar’s biography is included in the edition of Marquis who’s who in Science and Engineering and in the International Biographical Centre of Cambridge, England as “Outstanding Scientist of 21 ^st century”. His research interests include biomedical signal processing and image processing, analog and mixed signal VLSI Design and biometrics.

Suhas Gajre He received Ph.D. degree from Indian Institute of Technology, Delhi in Biomedical Engineering in 2007 and is currently working as Associate Professor in Electronics and Telecommunication Engineering Department at S.G.G.S. Institute of Engineering and Technology, Nanded, Maharashtra, India. He has published more than 10 research papers in peer reviewed Journals and Conferences. He is currently guiding 4 research scholars for their Ph.D. work. His research interests include Biomedical Signal and Image processing and Analog and Mixed signal VLSI Design.