Interval Type-2 Fuzzy Logic Controller to Control the Velocity and Angle of Inverted Pendulum

Published Online June 2014 in MECS

In the region of control systems [1], the inverted pendulum method is a normal problem. For assessing the justification of different kinds of control theories for mechanical systems, an inverted pendulum is familiar which is tough to be controlled by a valid time controller [2] [3]. An Inverted Pendulum is aneasy pendulum that is apprehended in an erect vertical position. It has a cart and a simple rod (with or without bob) [4]. Two equilibria, one of which is stable while the other is unstable [5] are found. Rotational single- arm pendulum, the double arm pendulum and the cart inverted pendulum, etc. [6] are the most well-known kinds of the inverted pendulum.

A multivariable, nonlinear, fast reaction, unsteady and high order system [7] [8] is the cart type inverted pendulum system. The general cart-double-pendulum system (CDPS) contains two-link manipulator mounted on a cart where only the cart is set in motion and the manipulator connects perform as a passive double pendulum [9]. In order toexamine and validatedissimilar control methods for dynamic systems with higher-order nonlinearities [10], the DIP is appropriate. The normal frequency of double inverted pendulum depends on the measurement lengthwise of the pendulum [11]. Under put into action degree one, for a class of under activated systems, that is, the quantity of control contributions is one less than that of degrees of independence [12].

The control setback of inverted pendulum is an additionalcomplicated [13] [14]. Henceto control the inverted pendulum systems, several control methods has been applied such as feedback stabilization, energy based control, bang-bang control, sliding mode control, robust control, hybrid control, partial linearization, PD, PID, and MPC [15][16]. Moreover these control methods are used to control of rockets, robots, fast moving ground vehicles and anti-seismic controls for buildings [17]. In the inverted pendulum [18], the steadiness problem is more significant.

Stabilization control is unfeasible if the two pendulums contain the similar natural frequency [19] for a paralleltype double inverted pendulum system. For the double inverted pendulum system [20], there are two main problems in the design of stabilizing controllers. The initial is wavering the pendulum up from the hang up position to the upright vertical position. The next problem consists in stabilization of the inverted pendulum about its unsteady equilibrium point [21]. Single inverted pendulum plan a stabilizing controllerwhich is a distinctive problem in control system [22]. For planning and examining controllers for these systems [9], quite a few approaches have been successful. They are genetic algorithms, incomplete feedback linearization and integrator back stepping, energy based approach [23]. In order to control the angle and velocity variation of the inverted pendulum, an IT2FLC control technique is proposed in this paper. The proposed technique is detailed in following section.

• II.    Modeling of inverted pendulum

The inverted pendulum system is one of the examples which iscommonly used in control system application. The reputation of the drives in part from the fact that it is unstable without control. Because, the pendulum will simply fall over if the cart isn't moved to balance it. In addition, the dynamic states of the system are nonlinear. The intention of the control system based controller is to balance the inverted pendulum by applying a force to the cart that the pendulum is attached. The free body diagram is illustrated in Fig.2.

From the free body diagram, the resultant force acting one the cart is obtained by summing the forces and the motion equation is described as follow:

d?x dx

=     +    + dt2 dt

Then, the governing force equation of the system is given below.

-( + )   +   +          - dt2 dt dt2

( )              (2)

To add the forces that acts perpendicular to the pendulum and getting the second motion equation of the system. Then, solving the system along with this axis greatly simplifies the mathematics and the present the equation as follow,

P sin 9 + N cos 9 - mg sin 9

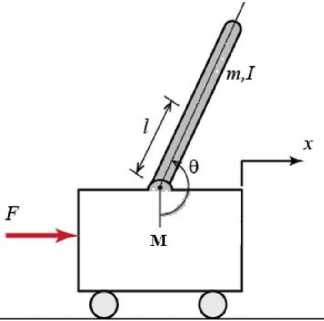
Fig. 1. Configuration of Inverted Pendulum

d2 x           d 29(3)

= m —cos 9 + ml — dt2

The centroid of the pendulum to get by adding the moments and the equation is described as below.

d 2 9

- Pl sin 9 - Nl cos9 = I—— dt2

Then, combining the equation (3) and (4), get the second governing equation which is expressed as following them, d 29

(I + ml )—— + mgl sin 9 = -mlcos

dt2

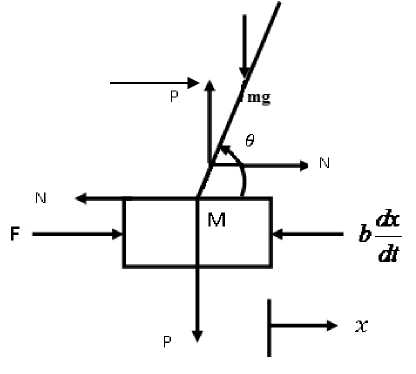
Fig. 2. Free body diagram

As the analysis and the control design techniques of the linear systems, the set of equation needs to be linearized. The vertical upward equilibrium position, 9 = П that are stays the system with the equilibrium position. This assumption should be reasonably valid while the pendulum not deviates from the desire position. Actually, the desired position of the pendulum not deviate more than 20⁰ from the vertical upward position. Let, ф indicate the pendulum deviation position from the equilibrium position i.e. 9 = П + ф . After, applying the equilibrium condition, the equations are modified as follow,

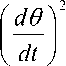
dф A 2 dt J

~ 0

In the above diagram (Fig.1 and Fig.2), F is the force applied to the cart, M is the mass of the cart, m is the mass of the pendulum, 9 is the angular position of the pendulum, x is the horizontal position of the cart and l is the length to pendulum center of mass.

After substituting the approximations (equation (6), the governing equation of the system is described as follow,

, d2 x          2 d 2Ф ml    =(I + ml )—— - mglф (7)

dt              dt

d2x , dx .d 2ф

(M + m)   + b - ml = 0

dt2 dt      dt2

The above mathematical derivations are used to model inverted pendulum. For controlling the angle and the velocity of the pendulum, the IT2FLS is used. While controlling the angle and velocity of the pendulum, optimized membership function is used as the input of the IT2FLS interference system.

Initially, the angle and velocity of the inverted pendulum are evaluated. After that, the change in the velocity and the change in angles are determined by taking the difference between the present and earlier error. By giving these calculated change of angle and change of velocity as the input to the IT2LS, the control output is calculated.

• III.    Controlling the pendulum angle and velocity using IT2FLS

Fuzzy logic controller is considered [29] to stabilize the inverted pendulum system. In this paper, IT2FLS is used for controlling the inverted pendulum angle and the velocity with minimum control deviation. Interval Type 2 fuzzy logic system includes fuzzifier, rule base, inference engine, type reductions and defuzzifier [30]. In the IT2FLS, the rule base part enclosed with antecendents and consequents parts and each rule inference output is a type-2 fuzzy set. The membership function limits are chosen with the help of the optimal velocity and the optimal angle. It is used for reducing footprint of uncertainties (FOU). A uniform weighting is supposed to symbolize a FOU since the mean changeable between m1 and m2, the gaussian function is measured with a standard deviation. The structure of the propsoed IT2FLS is given in fig. 3

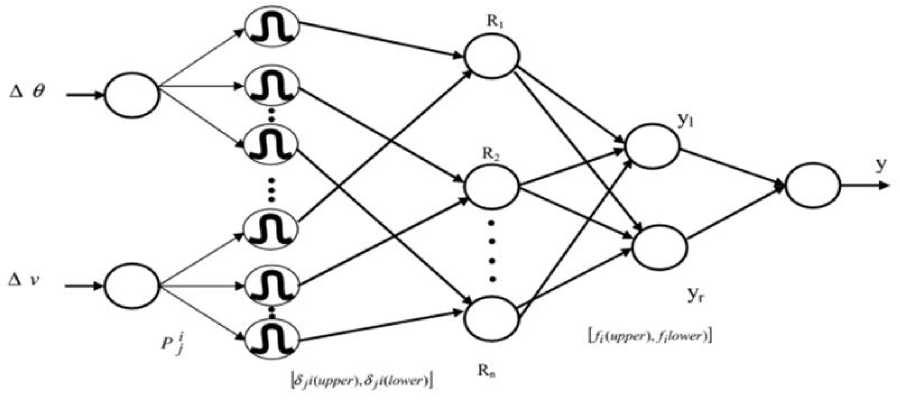
Fig. 3. Structure of proposed IT2FLS

Fuzzification is the first step of the IT2FLS, in which the crisp parameters of input A # and A V are converted and fuzzified into input interval type-2 fuzzy sets. In fuzzification, the change of angle and change of velocity are mapped to the linguistic labels of fuzzy sets. The membership functions of these fuzzy sets contain two inputs and one output. Here, the input vector is X i = ( x i , x 2 , x n ) and the if-then rules are specified in the following,

Rl = Ifx is Pi AND x^ is Pi

........... (12)

AND x is Pi THEN Yiis a

Where, Pj are the antecedents j = 1,2,3...n and Yj is the consequent of the ith rule. Then the Gaussian membership function (MF) is used which has a fixed standard deviation (SD) and uncertain mean that takes in the values in mj\,mj2] .The uncertainty of this membership functions can be represented in the bounded interval in terms of upper MF and lower MF. The Gaussian membership functions with uncertain mean described as,

’ ».....№Я

Where, m ij e [ m j 1 , m j 2 ] and j = 1,2,3... n , n is the number of antecedents. Then the i = 1,2,3... r , r is the number of rules. Then the upper and lower MF’s are specified as 5 j i ( upper) and 5 j i ( lower) respectively and described in the equation (14) and (15).

6- (upper) =

( T (^m j! ,D} xi J

1 m^ <  Xj < m j ₂  >

(T(mjv Djl;xj) x, > mj2)

And

(        )

(    ,   ;   )   ≤

(    ,    ;   )     >

+ 2 ⁺ 2

Where, the output of the each node is represented as in the lower and upper interval.

Here, by generating the rulethe fuzzy meet operation is done. For each node, two rules are generated by adding the upper membership functions seperately and lower membership function seperately. The output of a rule node is a firing strength FSⁱ , which is an IT2 fuzzy set. The firing strength is computed as follows,

=( (      ),  (      ))

M

^ fi ( upper ) ^ai

⁵ =_i = 1

y     M                                (20)

^ ft (upper)

i = 1

After the type-reduction process, the type-reduced sets are then defuzzified.

It is the last process of the IT2FLS where each output node corresponds to one output variable. Due to the output layer of an interval set, each and every node performs defuzzification process. The defuzzified output is denoted by y which is determined by taking the average of the nodes y ^q and y ^s .

Where,

n

(    )=∏  (    )

7 = 1

n

(   )=∏  (   )

7 = 1

y = y q + yi

Subsequently the obtained defuzzified control output of fuzzy system is given to inverted pendulum to reduce the deviations of the angle and the velocity of the pendulum and also the position of the pendulum are maintained that was close to the reference position.

Once the firing strength is obtained, the inference engine and the rule base are activated by the interval type-2 fuzzy sets to produce output. Then the input interval type-2 fuzzy sets and output interval type-2 are mapped by combining the fired rules using inference engine. Then outcome of the inference engine are processed by the type-reducer. The type-reducer combines the output sets and performs a centroid calculation which leads to type-1 fuzzy sets called the type-reduced sets.

The type reduced set of the interval type-2 FS is an interval type1 set which contains the left limit yl and right limit yr. The interval output of this layer is computed by each node present in this layer. The consequent a _i is a crisp value. Here we used a simplified type-2 reduction operation instead of the center-of-sets type reduction method. It considers only two embedded type-1 fuzzy sets with membership values, that is the outputs y ^q and y ^s are computed as follows,

M

^ ft (lower)ai

, q ₌ i = 1 _______________

M

^ ft (lower)

i = 1

• IV.    Results and Discussion

• 4.1    Performance analysis

The proposed IT2FLS was implemented in MATLAB/simulink working platform. The performance of the proposed IT2FLS was tested with inverted pendulum cart system. Here, the change of velocity and angles are calculated from their difference between the present state error and the previous error which are given to the IT2FLS. In the IT2FLS, the uncertainties are reduced and the optimal membership functions are determined. By using IT2FLS, the control output is generated for the inverted pendulum, which is controlling the angle and the velocity also, the stability position of the pendulum are determined. The performances of the proposed technique are evaluated and compared with PI controller, Fuzzy controller and ABC-Fuzzy controller[24].

Initially, the angles and velocity of the inverted pendulum performances are evaluated in normal position and illustrated in fig. 4(a) and 4(b) respectively. The output of IT2FLS is applied to the pendulum for controlling the angle and velocity. After that, evaluated the performances of the proposed method and illustrated in the figure 6. The performance of IT2FLS is illustrated in the fig. 6(a) and 6(b) respectively. Similarly, all the other methods were applied and illustrated the performance measures.

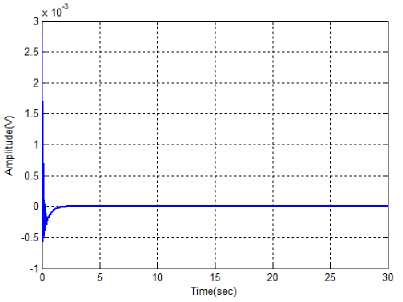
Fig 4(a). Performance of change of angle of inverted pendulum

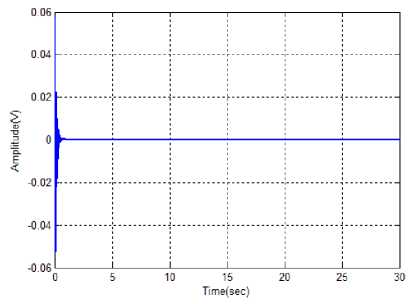
Fig.4(b). Performance of change of velocity of inverted pendulum

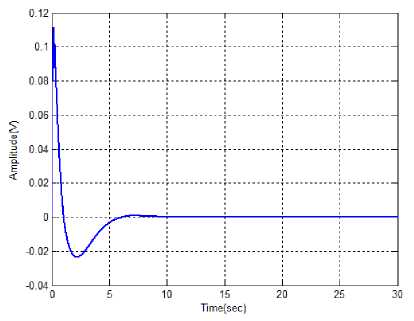
Fig. 5(a). Performance of pendulum angle using ABC-Fuzzy Controller

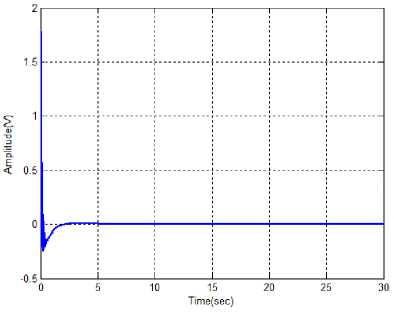
Fig.5(b). Performance of pendulum velocity using ABC-Fuzzy Controller.

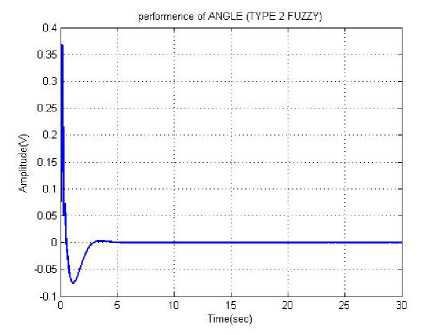
Fig. 6(a). Performance of pendulum angle using IT2FLS

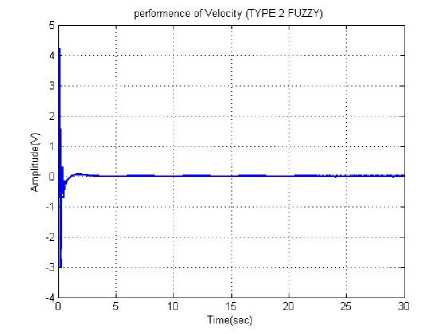
Fig. 6(b). Performance of pendulum velocity usingIT2FLS

From the above illustrations, the optimal value of pendulum angle and velocity are measured with the different time instants. Here, the various methods are used to calculate the optimal value of angle and velocity. The change of pendulum angle and the velocity is optimized with the time instant T=7sec and T=3sec respectively. Similarly, the optimized angle and velocity values are calculated in the fuzzy controller and IT2FLS. Therefore, the proposed controller achieves less time for optimizing the pendulum angle and velocity with compared to the other methods.

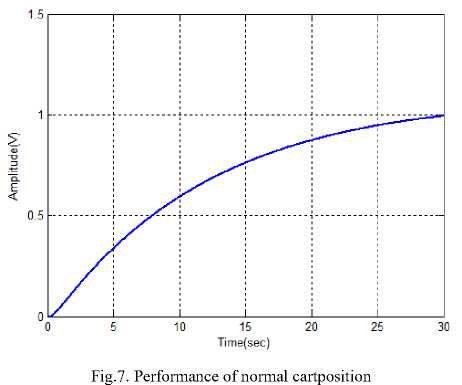
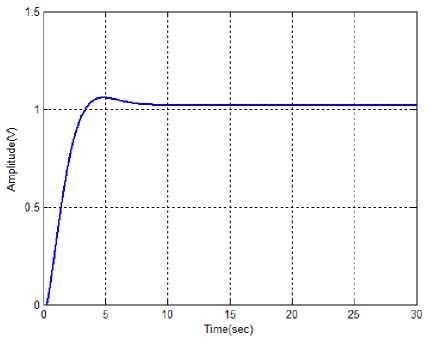
Fig. 8. Performance of Fuzzy cart position

by analyzing the cart positions within a short-span of time and small amplitude. Moreover, the rising time, settling time and peak time of the pendulum are evaluated for the proposed as well as existing methods.

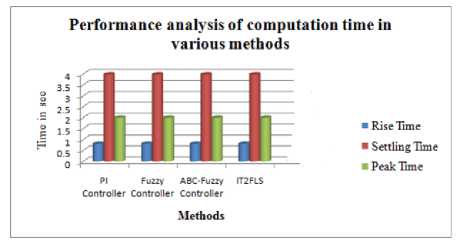
Fig. 11. Performance analysis of computation time in various methods

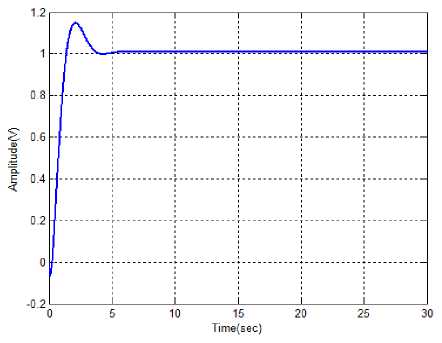
Fig.9. Performance of ABC-Fuzzy cart position

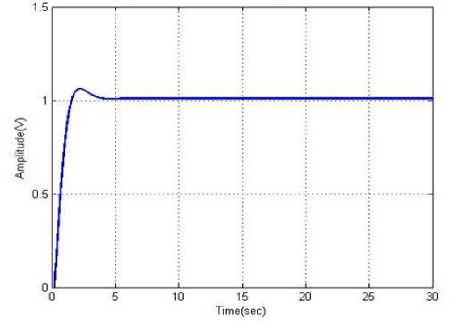
Fig. 10. Performance of IT2FLS cart position

The performance of the normal cart position is illustrated in the fig. 7. After applying various methods, the performances of the cart positions are varied with different amplitude. Here, the Fuzzy controller, ABC-Fuzzy controller and IT2FLS methods are applied for analyzing performances of the cart positions, which are illustrated in the fig. 8,9 and 10 respectively. Similarly, the performances of the cart positions are measured by using PI controller. The performance comparison results of existing methods with the proposed method shows that the proposed method outperforms the existing methods

From the above illustration (fig.11) describes the rising time, settling time and peak time of the PI controller, fuzzy controller, ABC-Fuzzy controller and IT2FLS respectively. Here, the peak value and peak time is not varied for most of these methods. The settling time of the proposed controller is 2.9800sec. The settling time of the PI controller, Fuzzy controller and IT2FLS is denoted as 3.9781sec, 3.9782sec,and 3.9781 sec respectively. So, the proposed controller reaches the settling time to take very less time when compared to the other controller. The proposed method reaches the actual system state very quickly. But, the PI controller takes more time to reach the settling time and the fuzzy controller deviated from the stability control position. Also, the proposed control technique maintains the system stability while changing the system mass. Then the rising time of the PI controller, Fuzzy controller, ABC-Fuzzy controller and IT2FLS are measured with their performances. Here, the rising time of the proposed controller is less than the other methods. Therefore, the proposed technique achieves the better performances when compared to other techniques. Similarly, the peak time is also measured in every method.

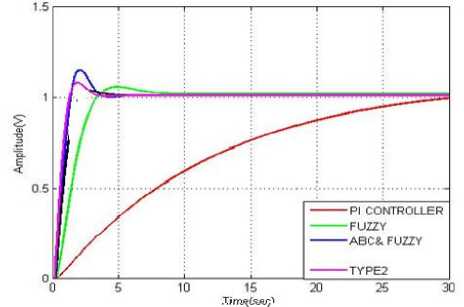
Fig. 12. Comparison performance of cart position of PI, Fuzzy, ABC-Fuzzy controller and proposed hybrid method

By using the proposed method, the stability cart position of the pendulum is analyzed. The performance of cart position after applying the proposed IT2FLC is described in Fig.10. Then, applying PI controller, fuzzy controller and ABC-Fuzzy controller, the stability performance of cart position is analyzed. The performance of proposed IT2FLC control approach is compared with PI controller, fuzzy controller andABC-Fuzzy controller. The comparison performance of cart position is illustrated in Fig.12. From the above illustrations, the proposed controller (IT2FLS) is the effective method for controlling the angle and the velocity deviation of the pendulum compared with the other methods. Therefore, the stability of the cart position is steadily preserved in the proposed method with compared to the PI controller, fuzzy controller andABC-Fuzzy controller.

• V.    Conclusion

In the paper, a IT2FLC was proposed for controlling the angle and velocity of the inverted pendulum. The proposed technique was implemented in the MATLAB/Simulink platform. Then, the performance of the proposed controller was compared with PI controller, fuzzy controller, and ABC-Fuzzy controller. The settling time, rising time and peak time of the proposed controller and other methods were determined. The comparative analysis shows the proposed controller effectively control the change of angle and velocity of pendulum. So, the steady state stability of the cart position of the pendulum is maintained better than PI controller, fuzzy controller and ABC-Fuzzy controller