Интервальная производная и начала недетерминистского дифференциального исчисления
Автор: Левин В.И.
Журнал: Онтология проектирования @ontology-of-designing
Статья в выпуске: 4 (10) т.3, 2013 года.
Бесплатный доступ
Показана возможность обобщения классического дифференциального исчисления на функции с интервальной неопределенностью переменных. Введено понятие производной от такой функции. Получены формулы, представляющие в явном виде интервальные производные любого порядка.
Интервал, интервальная функция, интервальная производная, интервальные вычисления, недетерминистское дифференциальное исчисление
Короткий адрес: https://sciup.org/170178494
IDR: 170178494 | УДК: 519.61
Текст научной статьи Интервальная производная и начала недетерминистского дифференциального исчисления
Проектирование и исследование свойств разнообразных систем обычно опирается на тот или иной подходящий математический аппарат. К настоящему времени создано большое число различных видов математического аппарата. Однако при всем их различии почти все они обладают одним общим свойством - применимостью только к полностью определенным (детерминированным) системам. В то же время встречающиеся на практике системы обычно характеризуются той или иной степенью неопределенности (недетерминированы). С целью построения и исследования таких систем чаще всего применяют математический аппарат теории вероятностей [1], теории нечетких множеств [2], интервальной математики [3]. В настоящей работе впервые предлагается новый математический аппарат для исследования недетерминированных систем - недетерминистское дифференциальное исчисление. Этот аппарат, в отличие от трех названных выше, нацеленных, в основном, на исследование статических систем, применим также к изучению динамических систем.
1 Вспомогательные математические сведения
Мы будем использовать в качестве вспомогательных сведений, прежде всего, основные математические сведения из алгебры интервальных чисел [3, 4]. В этой алгебре в качестве операндов берутся замкнутые вещественные интервалы, определяемые как множества всех вещественных чисел между нижней и верхней границами интервала, включая сами эти границы
-
(1) ~ = [ a 1 ,a 2] = { a | a 1 < a < a 2} .
Эти операнды естественно называть интервальными числами. Операции ° над интервальными числами а = [ a 1 , a 2 ], b = [ b 1 , b 2 ] вводятся как прямые теоретико-множественные обобщения соответствующих операций над вещественными числами a , b , т.е.
-
(2) ~ ° b = { a ° b | a е ~, b е b } .
Таким образом, основные алгебраические операции над интервальными числами определяются следующими формулами у _ . . у. у _ . .у.
-
(3) k • a = { k • a | a & ~},
_. у . . -. . У. _ . . у .У.
На основе определений (3) операций над интервальными числами можно вывести следующие формулы для вычисления результатов этих операций [3]
a + b = [ a 1 , a 2 ] + [ b 1 , b 2 ] = [ a 1 + b 1 , a 2 + b 2 ], ~ - b = [ a 1 , a 2 ] - [ b 1 , b 2 ] = [ a 1 - b 2, a 2 - b 1 ], f [ kax , ka^ ], k > 0, (4) k • a = k • [ a ,, a 2 ] = 12
-
12 [ [ ka 2, ka 1 ], k < 0,
~ • b = [ a 1 , a 2] • [ b 1 , b 2] = [min( a i • b j ),max( a i • b j )], i . j i , j
УI b = [ a 1 , a 2]/[ b 1 , b 2] = [ a 1 , a 2] • [1/ b 2,1I b 1 ].
Также в качестве вспомогательного нам потребуется понятие интервальной функции [5], которая вводится как однозначное отображение множества замкнутых вещественных интервалов { у }, у = [ x 1 , x 2] вида (1) на множество замкнутых вещественных интервалов {у}, f = [ У 1 , У 2] этого же вида. Символически интервальная функция записывается в виде
-
(5) f = f (У) ,
где, аналогично числовым функциям, у называется интервальной независимой переменной (интервальным аргументом), у - интервальной зависимой переменной, f - интервальной функцией.
Введем теперь понятие предела интервальной функции (5). Рассмотрим независимую переменную f = [ x 1 , x 2] этой функции. Будем говорить, что переменная ~ в процессе своего изменения неограниченно приближается к некоторому предельному интервалу f 0 = [ x 01 , x 02 ] , если в указанном процессе x 1 неограниченно приближается к x 01, а x 2 неограниченно приближается к x 02 . Символически неограниченное приближение f x к f x 0 показывается как
-
(6) (f ^ f0) = ( x 1 ^ x 01, x 2 ^ x 02) = (lim x1 = x 01,lim x 2 = x 02) .
Совершенно аналогично независимой переменной ~ зависимая переменная ~ интервальной функции (5) в процессе своего изменения может неограниченно приближается к некоторому предельному интервалу f 0 = [ y 01, у 02 ], т.е.
-
(7) (f ^ f 0 ) = ( У 1 ^ У 01 , У 2 ^ У 02 ) ■
При этом если неограниченное приближение зависимой переменной ~ интервальной функции (5) к у 0 вызвано неограниченным приближением независимой переменной ~ этой функции к у0, будем говорить, что предел интервальной функции (5) при ~ , стремящемся к у0, равен интервалу у 0. Символически это записывается в виде
-
(8) lim У = У о или, по-другому, lim f (f) = У о ■
у ^у0 У ^У0
Если интервальная функция (5) непрерывная, т.е. как нижняя, так и верхняя границы интервала у (зависимой переменной) являются непрерывными функциями нижней и верхней границ интервала у (независимой переменной), то предел функции (5) равен значению функции от предельного значения аргумента, или, в символической записи,
-
(9) Jim / (у) = у (у о ).
x ^ x о
2 Интервальная производная функция
Рассмотрим теперь произвольную интервальную функцию (5). Будем считать ее непрерывной. Зафиксируем некоторое значение х о = [ x 01 , x о2 ] независимой переменной. Этому значению, в силу непрерывности нашей функции, будет соответствовать фиксированное значение функции у о = / ( у о) . Определим теперь приращения независимой и зависимой переменных нашей функции относительно их указанных фиксированных значений
∆ х = x - x о, Aу = у - у о = У(x ) - У(x о)
и составим отношение второго приращения к первому
A y
А х
^ ^ Г/^Х Г/^ X у - у о _ У(x ) -У(x о)
-^ ^
x - x о
-^ ^
x - x о
Возьмем предел отношения (11) при неограниченном приближении независимой переменной у к ее фиксированному значению уо:
А у lim —— .
x ^ x о A x
Предел (12), если он существует, будем называть производной интервальной функцией от исходной интервальной функции (5) в точке уо или, коротко, интервальной производной от функции (5) и обозначать у ~ или / - ( у ) . Таким образом,
у у = У у (у) = lim А У . x о x о у ^ у о A x
Условие существования интервальной производной интервальной функции определяется следующей теоремой.
Теорема 1. Для того чтобы в точке уо существовала интервальная производная от интервальной функции (5), определяемая формулами (10)-(13), необходимо и достаточно, чтобы в некоторой окрестности этой точки, включая ее саму, все значения независимой переменной у функции были невырожденными интервалами (т.е. интервалами с несовпадающими верхней и нижней границами).
Доказательство. Из выражения (11) интервальной функции, предел которой есть интервальная производная в точке уо, видно, что эта производная существует только тогда, когда в некоторой окрестности указанной точки, включая ее саму, все возможные значения знаменателя выражения (11) не равны нулю. Но знаменатель выражения (11), согласно формуле (4) разности интервалов, равен интервалу у - уо = [ x 1, x 2] -[ x о1, x о2] = [ x 1 - x о2, x 2 - x о1].
Правый интервал равен нулю (нулевому интервалу [о,о] ) только при условии
X1 = X 02 , X 2 = X 01, равносильном следующему
X 1 = X oi = X 2 = X 02
или
X = X 0 = [ X , X J , что означает вырожденность интервалов ~,~0.
Ввиду произвольности выбранной точки ~0 , последнее означает, что для существования интервальной производной в точке ~0 необходимо и достаточно, чтобы в некоторой окрестности этой точки, включая ее саму, все возможные значения независимой переменной функции ~ были невырождены. Что и требовалось доказать. •
Интервальная производная от интервальной функции (5), определяемая для произвольной точки ~ 0 формулами (10)-(12) в виде предела, может быть выражена также в конечном виде через значения независимой ~ и зависимой У = f (~) переменных этой функции в указанной точке. А именно, справедлива следующая теорема.
Теорема 2. Интервальная производная от непрерывной интервальной функции (5), определяемая для произвольной точки ~0 формулами (10)-(13) в виде предела, может быть выражена в конечном виде через значения независимой ~ и зависимой У = f (~) переменных этой функции в указанной точке следующим образом
У
~
У У> - fi 0 (~) =
f (У 0 ) - f (У 0 )
~ x 0
-
~ x 0
.
Примечание 1. При первом взгляде выражение (14) может показаться неопределенностью вида 0/0. Но это впечатление неверно, поскольку, согласно теореме 1, у любой существующей в точке ~0 интервальной производной интервал ~0 невырожден и потому, в соот ветствии с формулой (4) для разности интервалов, разность ~0 - ~0 не равна нулю (нулевому интервалу [0,0]). Точно также не равна нулю разность f (~0) - f (~0).
Доказательство. Согласно определению интервальной производной в точке ~0 (10)
-
(13) она может быть записана в виде предела
У У = f У (У) = lim
X 0 X 0 У <У
X —т X 0
f (У) - f (У 0 )
~ ~
X - X 0
.
В процессе предельного перехода в правой части равенства (15) У неограниченно приближается к У0, а f ( У ) , в силу непрерывности интервальной функции f - к f ( У 0) . Таким образом, предел в правой части (15) равен
lim f (У) - f (У 0 ) = f (У 0 ) - f (У 0 ) У . У У У У У
X — X 0 X - X 0 X 0 - X 0
Подставив полученное значение предела из равенства (16) в выражение (15), будем иметь формулу (14). Что и требовалось доказать. •
Итак, выражение интервальной производной функции (14) представляет ее через исходную (первообразную) интервальную функцию (5). При этом, поскольку в указанном выражении точка У 0 , в которой определяется производная, произвольна, выражение это можно переписать в общем виде следующим образом:
~ ~
-
(17) yL ее /7(~) = f M- f M
( ) y У У (x ) , x-x где ~ - произвольное значение независимой переменной непрерывной интервальной функции (5) из ее области определения, при котором интервальная производная этой функции существует. Как видно из формулы (17), интервальная производная выражается непосредственно через исходную (первообразную) интервальную функцию простой алгебраической формой, что, конечно, упрощает процесс вычисления производной. Этот эффект отсутствует при нахождении обычных производных, фигурирующих в традиционном дифференциальном исчислении детерминированных функций [6].
3 Интервальные производные высших порядков
Производная f f (~) от интервальной функции f (~) , введенная выше в пункте 2, также является интервальной функцией, притом зависящей от того же самого интервального аргумента ~. Это позволяет продолжить процесс взятия интервальных производных функций, получив сначала вторую производную f X (~ ) (производную от первой производной f f (~) )
-
(18) f x = f x '(~) = [ f У (~)] ~ ,
затем третью производную f f (x ) (производную от второй производной f f (x ) )
-
(19) f y”- f Д~ ) = [ f f (~ )] f
и т.д., вплоть до интервальной производной любого n -го порядка, определяемой как производная от производной n - 1 порядка
-
(20) f f” 1 = f У ’ (f) = [ f У - 1>(f)] f .
Условие существования интервальной производной любого n -го порядка определяется следующей теоремой.
Теорема 3. Для того чтобы в точке ~0 существовала интервальная производная n -го порядка ( n = 2,3,...) от интервальной функции (5), определяемая формулами (18)-(20), необходимо и достаточно, чтобы в некоторой окрестности этой точки, включая ее саму, все значения независимой переменной f x функции были невырожденными интервалами.
Доказательство. По теореме 1, для существования в точке ~0 производной 1-го порядка от функции (5) необходимо и достаточно невырожденности всех интервалов, служащих значениями независимой переменной ~ этой функции в некоторой окрестности точки У 0. Но производная 1-го порядка от функции (5) имеет ту же независимую переменную f x , что и сама функция. Поэтому, согласно теореме 1, для существования в точке f x 0 производной от производной 1-го порядка функции (5) (т.е. производной 2-го порядка от интервальной функции (5)) необходимо и достаточно выполнения того же условия, что и для существования в точке f x 0 производной 1-го порядка от функции (5), т.е. невырожденности всех интервалов, являющихся значениями независимой переменной f x функции (5) в некоторой окрестности точки f x 0 . Продолжая по цепочке наши рассуждения, придем к необходимым и достаточным условиям существования в точке f x 0 производной n -го порядка от функции (5) в той форме, в которой они сформулированы в теореме 3. Что и требовалось доказать. •
Интервальная производная любого n -го порядка от интервальной функции (5), определяемая формулами (18)-(20) итеративно, может быть выражена также в конечном виде, аналогично выражению в конечном виде (17) интервальной производной 1-го порядка. Такие выражения основываются на следующей теореме.
Теорема 4. Интервальная производная n -го порядка ( n = 2,3,...) от интервальной функции (5) может быть выражена в конечном виде через интервальную производную ( n - 1) -го порядка от этой функции (если она непрерывная) и независимую переменную ~ в следующем виде
~ ~ n ) - 7 ~ n ) (~) =
7 ~ n - 1)(~) - 7 ~ n - 1)
^ г-^
x - x
(~)
—, n = 2,3,...
Доказательство теоремы получается с помощью формулы (1 7), если подставить в нее в качестве функции 7 (~) производную ( n - 1) -го порядка 7 ~n - 1)(~) и учесть еще, что производная 1-го порядка от / ~( n - 1) (~) согласно определению (20) есть производная n -го порядка Л * n ) (~) .
С помощью теорем 2 и 4 можно последовательно получить конечные выражения для интервальной производной 2-го порядка
~
~ ~ - -" (~) =
7 ~ (~) - 7 ~ (~)
^ ~ x-x
7 (~) - 7 (~) 7 (~) - 7 (~)
- x - x_________x - x .
x - x
для интервальной производной 3-го порядка
7 (~) - 7 (~) 7 (~) - 7 (~)
-
7 (~) - 7 (~) 7 (~) - 7 (~)
-
(23) ~ X - 7 ”(~) =
,/~'(~) - 7 x '(~)
■^ ^
x - x
■^ ^
x - x
^ ^ ^ ^
x - x x - x
■^ ^
x - x
■^ ^
x - x
■^ ^
x - x
■^ ^
x - x
и т.д. Отметим, что все эти выражения аналогичны конечному выражению (17) для интервальной производной 1-го порядка.
Примечание 2. Выражения (22), (23),... интервальных производных высших порядков кажутся с первого взгляда суперпозициями неопределенностей вида 0/0, однако, по причине, указанной в примечании 1, не являются таковыми. Заметим также, что эти выражения не могут быть преобразованы к более простому виду с помощью эквивалентных преобразований, поскольку в алгебре интервальных чисел [3] не выполняются эквивалентности типа
~ ~
a ± b ) c = ac ± bc ;
a ± b a b
= ± .
c cc
4 Вычисление интервальных производных
Доказанные выше выражения интервальных производных (17)-(23) являются аналитическими выражениями, имеющими вид суперпозиций операций над интервальными переменными. Эти выражения удобны для теоретического изучения интервальных производных. Что касается вычисления таких производных, то использование здесь выражений (17)-(23) оказывается неудобным, поскольку оно предполагает объемную работу с весьма громоздкими формулами интервальной математики (4), которые и позволяют выразить, в конце концов, интервальную производную в виде интервального числа с явно выраженными в числовой форме нижней и верхней границами. Однако гораздо удобнее вычислять интервальные производные по формуле, выражающей сразу в явном виде нижнюю и верхнюю границы интервального числа, служащего значением интервальной производной. Эта формула выводится ниже.
Теорема 5. Интервальная производная от непрерывной интервальной функции (5), выражаемая для произвольной точки ~ формулой (17) в виде суперпозиции операций над интервальными переменными, может быть также представлена явно в виде интервала, нижняя и верхняя границы которого выражены через нижнюю и верхнюю границы интервальных независимой ~ = [ x 1 , x 2] и зависимой у = [ у 1 , у 2] переменных этой функции в точке ~ следующим образом
г-~-
У x - У У (~) =
У 2 - У 1
У 2 - У 1
х 2 - x 1
x 2 - x 1
Доказательство. Будем исходить из выражения интервальной производной от интервальной функции (5) формулой (17). Представим указанную функцию в явном виде интервала
~ (~) = [ f , (~), f 2 <~)] - [ У 1 , У 2 ] - У .
Здесь
У 1 = f | (хX У 2 = f 2 (~)
есть соответственно нижняя и верхняя границы интервальной зависимой переменной функции (5). Аналогично представим интервальную независимую переменную ~ :
~ = [ x 1 , x 2 ].
После проведения необходимых подстановок выражение (17) интервальной производной от интервальной функции (5) примет вид
%- f ‘ (У)
У - У = [ У 1 , У 2] - [ У 1 , У 2] ~ - ~ [ x 1 , x 2 ] - [ x 1 , x 2 ]
Разности интервалов в числителе и знаменателе выражения (29) по формуле (4) представим в виде интервального числа
-
(30) [ У 1 , У 2] - [ У 1 , У 2] = [ У 1 - У 2 , У 2 - У 1] , [ x 1 , x 2] - [ x 1 , x 2] = [ x 1 - x 2 , x 2 - x 1] .
Подставив выражения (30) в (29), получим представление интервальной производной в виде частного двух интервалов
~f
У ~
- f ~ (~)
[ У 1 - У 2 , У 2 - У 1] [ x 1 - x 2, x 2 - x 1 ]
В свою очередь, выражение (31) можно, согласно формуле (4), представить в виде следующего произведения двух интервалов
У
-
(32) у ~ - ff x ( ~ ) = [ У 1 - У 2 , У 2 - У 1] • [ 1/ ( x 2 - x 1), 1/ ( x 1 - x 2)] .
Перемножая интервалы в правой части (32) по соответствующему правилу (4), получим
я - ж ~) =
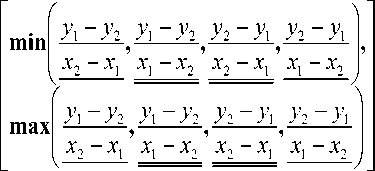
Одинаково подчеркнутые члены в выражении (33) равны. Оставив из каждых двух равных членов по одному, представим выражение (33) в более простом виде
~
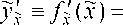
min
У 2 — У 1
У 2
—
У 1 )
max ■
—
У 1
У 2
— У 1
X
V x 2
— x i
x 1 - x 2 ;
V x 2
— x 1
x i - x 2 ;
Два члена в круглых скобках формулы (34) различаются лишь знаком, причем (с учетом того, что x 2 > x 1 , y 2 > y 1 ) левый член положителен, а правый - отрицателен. Так, из (34) получается простейшее выражение интервальной производной от интервальной функции (5)
~ ~ - f (~) =
У 2 — У 1 x 1 — x 2
У 2 — У 1 x 2 — x 1
С учетом того, что x 1 — x 2 = — ( x 2 — x 1 ), выражение (35) окончательно переписывается в виде
~ ~ - №) =
У 2 — У 1 x 2 — x 1
У 2 — У 1
x 2 — x 1
что и требовалось доказать. •
Аналогичное (25) явное выражение интервальной производной функции, дающее сразу в явном виде нижнюю и верхнюю границы интервального числа - значения этой функции -справедливо и для производных высших порядков. Это выражение приведено ниже.
Теорема 6. Интервальная производная любого n -го порядка от непрерывной интервальной функции ~ = f (~) вида (5), выражаемая для произвольной точки ~ формулой (21) в виде суперпозиции операций над интервальными переменными, может быть представлена в указанной точке также в явном виде интервала, нижняя и верхняя границы которого выражены через нижнюю и верхнюю границы интервальных независимой переменной ~ = [ x 1 , x 2] и промежуточной переменной - производной ( n — 1) -го порядка ~ ( n — 1) = [ У 1 n — 1) , У 2 n — 1) ] от интервальной функции (5) следующим образом
y y) . f ~ n > (?) =
( n — 1) ( n — 1)
у 2 — у 1
x 2 — x 1
( n — 1) ( n — 1)
у 2 — у 1
x 2 — x 1
Доказательство теоремы 6 аналогично доказательству теоремы 5, с той разницей, что в качестве исходного выражения искомой интервальной производной n -го порядка от интервальной функции (5) берется формула (21), тогда как в случае теоремы 5 исходным выражением искомой интервальной производной 1-го порядка от функции (5) служит такая же по форме формула (17).
Используя формулу (37), нетрудно получить простые явные выражения типа (25) для интервальных производных 2-го, 3-го и т.д. порядка от интервальной функции (5). Действительно, для интервальной производной 2-го порядка из (37) имеем
x
x x - f ~ (~ ) =
у 2 - у ‘
у 2 - у 1
x 2 - x 1
x 2 - x 1
Подставляя в соотношении (38) значения нижней и верхней границ интервальной производной 1-го порядка из (25) в виде
x X - ~ x (X) =
2( у 2 - У 1 ) 2( у 2 - У 1 ) ( x 2 - x i ) ( x 2 - x i )
Аналогично, для интервальной производной 3-го порядка из (37) имеем
x x - ~(~) =
-
у 2'
-
у 2
у 2
-
у 1
x 2 - x 1
x 2 - x 1
Как и в предыдущем случае, подставляя в формулу (41) значения границ интервальной производной 2-го порядка из (40) в виде
. .=- 2^221.) у = 2( у 2 - у i ) 1 ( x 2 - x 1 )2 , 2 ( x 2 - x 1 )2
будем, после необходимых эквивалентных преобразований, иметь
x x - f x"(x) =
4( у 2 - у 1 ) 4( у 2 - у 1 ) ( x 2 - x 1 ) ( x 2 - x 1 )
Продолжая этот процесс для интервальных производных 4-го, 5-го и последующих порядков, приходим к следующему общем результату.
Теорема 7. Интервальная производная любого n -го порядка от непрерывной интервальной функции ~ = f (~) вида (5), выражаемая для произвольной точки ~ формулой (21) в виде суперпозиции операций над интервальными переменными, может быть представлена в указанной точке также в явном виде интервала с явно выраженными нижней и верхней границами вида (25), (40), (43)
~ ( П ) ~ ( П )
у Г- f~ )( x ) =
2" - 1( у 2 - у 1 ) ( x 2 - x 1 ) n
2 n - 1( у 2 - у 1 ) ( x 2 - x 1 ) n .
Здесь x 1 , x 2 - нижняя и верхняя границы интервальной независимой переменной x = [ x 1 , x 2 ] в точке взятия производной от функции x = f (~) , а у 1 , у 2 — нижняя и верхняя границы интервальной зависимой переменной ~ = [ у 1 , у 2 ] этой функции в той же точке.
Сводка полученных явных выражений интервальных производных функций различных порядков приведена в таблице 1.
5 Возможные применения
Предложенный в настоящей работе математический аппарат недетерминистского дифференциального исчисления может быть успешно применен к построению и количественному изучению свойств различных недетерминированных систем динамического типа, т.е. сис- тем, количественные характеристики которых известны с той или иной степенью неопределенности и вдобавок изменяются во времени. Такие системы широко распространены в экономике, социологии и экологии. Они также встречаются в технике и технологиях. Методика применения указанного математического аппарата к названным системам основана на предположении о том, что все параметры изучаемой системы определяются с точностью до интервалов возможных значений. При этом статические звенья характеризуются постоянными интервалами возможных значений их параметров, а динамические звенья - переменными интервалами этих значений. В соответствии с этим для построения действующей математической модели изучаемой недетерминированной системы и последующего математического моделирования этой системы нужно:
-
1) взять (построить) математическую модель идеального (детерминированного) прообраза системы, которая получается в предположении, что все параметры системы заданы точно, соответственно чему статические звенья системы имеют постоянные точечные значения параметров, а динамические звенья - переменные точечные значения параметров; таким образом, в этой модели изучаемые характеристики системы принимают точечные постоянные и переменные значения и могут быть представлены в виде суперпозиции обычных алгебраических операций над точно известными постоянными и переменными значениями параметров звеньев системы;
Таблица 1 - Явные выражения интервальных производных
|
Функция |
Обозначение функции |
Явное выражение функции |
||
|
Исходная интервальная функция |
У = f ( x X x = [ x 1 , x2 ],У = [ У 1 , У 2] |
[ У 1 , У 2 1 = f [ x 1 , x 2 1 или [ У 1 , У 2 1 = [ f l ( x 1 , x 2 ), f 2 ( x 1 , x 2 )] |
||
|
Интервальная производная функция 1-го порядка |
~ - f; (~) или yx" - f ^t?) |
- У 2 - У 1 У 2 - У 1 "1 x 2 - X 1 , x 2 - X 1 |
||
|
Интервальная производная функция 2-го порядка |
~ ~ = / ДО) или ~ ~2> - f^x ) |
' 2( У 2 - У 1 ) 2( У 2 - У 1 ) ' |
||
|
_ ( x 2 - x 1 )2,( x 2 - x 1 )2 _ |
||||
|
Интервальная производная функция 3-го порядка |
~ ? - f T(~) или ~ - f ,<3> (~) |
' 4( У 2 - У 1 ) 4( У 2 - У 1 ) ' _ ( x 2 - x 1 )3 ( x 2 - x 1 )3 _ |
||
|
Интервальная производная функция - -го порядка |
У < - > - f x n ) (~) |
■ 2 n - 1( У 2 - У 1 ) 2 n - 1( У 2 - У 1 ) 1 _ ( x 2 - x 1 ) n ( x 2 - x 1 ) n J |
||
-
2) заменить в полученной на шаге 1 математической модели точечные значения параметров соответствующими интервалами возможных значений данных параметров; обычные производные в исходной детерминированной системе заменяются соответствующими интервальными производными, в результате получаем математическую модель собственно изучаемой системы, все параметры которой определяются с точностью до интервалов возможных значений; в этой модели изучаемые характеристики системы принимают интервальные значения и могут быть представлены в виде суперпозиции интервальных операций (3) над интервалами - значениями параметров звеньев системы;
-
3) используя соотношения (4), выражающие результаты элементарных преобразований интервалов, представляем интервальнозначные характеристики недетерминированной системы в явной форме интервала F = [ f 1 , f 2 ] , нижняя f । и верхняя f 2 границы которого являются обычными (детерминированными) функциями от нижних и верхних границ интервалов - параметров звеньев системы. После этого математическое моделирование изучаемой недетерминированной системы по любой ее интервальной характеристике F = [ f . , f 2] сводится к анализу двух обычных детерминированных функций f 1 , f 2 .
Пример. Рассмотрим простейшее применение предложенного математического аппарата в экономике. Пусть у = f (х) - некоторая детерминированная функция, показывающая зави симость одного экономического показателя у от другого х [7]. Тогда эластичностью Ex (у) этой функции называется предел относительного приращения функции y к относительному приращению аргумента (независимой переменной) х при Дх > 0, т.е.
п х (Д У ДХх ) х Д у х ,
-
(45) Ех ( У) = llm Л ■ У х .
Д х ^ 0 ^ у / х ) у Д х ^ 0 Д х у
Здесь у х - производная от функции у = f ( х ) по переменной х . Эластичность функции показывает приближенно, на сколько процентов изменится значение функции у = f ( х ) при изменении значения аргумента х на 1%. Например, если функция у = f ( х ) показывает зависимость спроса у на товар от его цены х , то эластичность этой функции Ех ( у ) есть коэффициент, приближенно показывающий, на сколько процентов изменится спрос на товар при изменении его цены на 1%. Аналогично, если функция у = f ( х ) показывает зависимость издержек производства y от объема выпускаемой продукции x , то эластичность этой функции Ех ( у ) показывает приближенно, на сколько процентов изменятся издержки производства при изменении объема выпускаемой продукции на 1%. Наконец, если изучаемая нами функция у = f ( х ) есть зависимость себестоимости единицы продукции у от стоимости всей выпускаемой продукции х , то эластичность данной функции Ех ( у ) показывает приближенно, на сколько процентов изменится себестоимость единицы продукции при изменении стоимости всей продукции на 1% и т.д.
Положим теперь, что (как это часто бывает на практике) независимая x и зависимая y переменные рассматриваемой экономической функции у = f ( х ) определяются не точно, а с точностью до интервалов возможных значений. Тогда эта функция из детерминированной превращается в недетерминированную (интервальную) функцию у = f (~) вида (5), где у = [ х 1 , х 2] - независимая интервальная переменная (интервальный аргумент), а у = [ у 1, у 2] -зависимая интервальная переменная. Построим теперь математическую модель получившейся экономической системы, используя описанный выше трехшаговый алгоритм.
-
1) Исходная математическая модель идеальной (детерминированной) системы уже есть, она описывается функцией эластичности системы (45) с точными значениями переменных x и у .
-
2) Заменяем в математической модели, установленной на шаге 1, точные значения параметров х и у соответствующими интервалами их возможных значений у = [ х 1 , х 2] и у = [ у 1 , у 2] , а детерминированную производную 1-го порядка у 'х - соответствующей интервальной производной у ~ , явное выражение которой в виде интервала дается формулой (25). В результате получаем математическую модель искомой недетерминированной
экономической системы - ее интервальную функцию эластичности - в виде следующей суперпозиции интервальных операций над интервалами - параметрами системы:
~ X
Е ~ (~) = 4 • ~ ~ = y
[ х 1 , X 2 ]
[ У 1 , У 2]
У 2 - У 1
X 2 - X 1
У 2 - У 1
X 2 - X 1
-
3) После вычисления выражения (46) по формулам (4) элементарных преобразований интервалов, с учетом положительности значений х 1 , х 2, у 1 , у 2 в экономических системах, получим окончательно следующую математическую модель искомой системы
Е ~ (~) =
х 2( У 2 - У 1 ) X 2( У 2 - У 1 ) У 1( х 2 - х 1 ) , У 1( х 2 - X 1 ).
Заключение
В настоящей статье показана возможность обобщения классического дифференциального исчисления на случай недетерминированных функций, в которых переменные задаются с точностью до интервалов возможных значений. Новое дифференциальное исчисление идейно близко к классическому дифференциальному исчислению, в частности, производная функция показывает скорость изменения первообразной функции относительно ее аргумента. Однако форма нового исчисления существенно иная. Главные отличия состоят в том, что, во-первых, производная любого порядка является интервальной функцией, в которой все переменные имеют вид интервалов и, во-вторых, производная любого порядка выражается в явном виде через значения независимой и зависимой переменных первообразной функции.
Список литературы Интервальная производная и начала недетерминистского дифференциального исчисления
- Гнеденко, Б.В. Курс теории вероятностей: Учебник, 8-е изд. испр. и доп. / Б.В. Гнеденко. - М.: Эдиториал УРСС, 2005. - 448 с.
- Заде, Л.А. Понятие лингвистической переменной и его применение к принятию приближенных решений / Л.А. Заде. - М.: Мир, 1976.- 165 с.
- Алефельд, Г. Введение в интервальные вычисления / Г. Алефельд, Ю. Херцбергер. - М.: Мир, 1987.- 356 с.
- Левин, В.И. Интервальные методы оптимизации систем в условиях неопределенности / В.И. Левин. - Пенза: Изд-во Пензенского технологического института, 1999. - 101 с.
- Левин, В.И. Оптимизация в условиях интервальной неопределенности. Метод детерминизации / В.И. Левин // Автоматика и вычислительная техника. - 2012. - № 4. - С. 17-25.
- Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления. Т. 1. / Г.М. Фихтенгольц. - М.: ФИЗМАТЛИТ, 2001. -616 с.
- Кремер, Н.Ш. Высшая математика для экономистов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. - М.: ЮНИТИ, 2001.-471 с.


