Интервальные оценки для коэффициента пьезопроводности по данным томографической обработки данных гидродинамического прослушивания скважин

отличается специализированной – веерной системой наблюдений за депрессией на пласт и ее откликом в соседних скважинах. Данное направление называется гидродинамической томографией получило развитие в работах [7]. Исходные данные, используемые для реализации алгоритма гидродинамической томографии могут быть получены, во-первых, непосредственным наблюдением за процессом депрессии на пласт и откликом на нее по всем доступным для наблюдения соседним скважин. В этом случае возникает аналог веерной томографической системы [8]. Те же данные могут быть синтезированы из наблюдений за историей разработки месторождений и создании ее модели как имитационной упругой модели [9, 10]. Может быть использован симбиоз первого и второго, что составляет содержание этапа подготовки томографических данных.

ПОСТАНОВКА ЗАДАЧИ

Специфика данных приводит к существованию значимых погрешностей в их значениях. Кроме того, реализация алгоритма гидродинамической томографии основана на обращении интегрального уравнения для поля времен (времена прихода возмущений – откликов по системе скважин от депрессии в скважинах по которым идет закачка) что является некорректной задачей. В итоге наличие погрешностей в данных приводит к значимым отклонениям в вариантах решения обратной задачи. Практический интерес в этих условиях будут иметь только те распределения коэффициента пьезопроводности, для которых имеется оценка их погрешностей. Однако задача оценки погрешностей в решении некорректных задач является логически недоопределенной и требует развития новых, специализированных подходов. Логическая недоопределенность состоит в том, что в любом диапазоне неопределенности данных можно выделить элемент, на котором значение обратного оператора неограниченно. Поэтому строго говорить о погрешности в решении, наследуемой погрешностями в данных невозможно без изменения принципов рассмотрения операторов.

ОСНОВНЫЕ АЛГОРИТМЫ

Пространственное распределение коэффициента пьезопроводности к (^) определяет время движения экстремальной точки (точки перегиба) восстановления давлений, между вы- деленными парами скважин. Движение происходит по траектории Lr r , соединяющей скважины, расположенные в точках ( rn, rend ). Эта траектория такова, что интервальное время движения экстремальной точки между (rn ) и

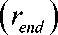
Т( rn, rend ) = J

L ( r n . r end )

минимально. Этим требованием определяется траектория движения экстремальной точки L ( r n , r_{e nd} ) . l ( ^ ) — длина пройденного пути

) . Задача гидродина-

от начальной точки r n до промежуточной ^ по траектории L ( r n , r end ) . Задача гидродинамической томографии состоит в нахождении

(приближенном) распределения коэффициента пьезопроводности к (^), как функции пространственной координаты ^ по результатам измерения всех доступных для измерения ин- тервальных времен т = {т} ; Т = Т (r‘n, r‘md). Эта задача решается традиционным методом последовательных приближений на основе линеаризации (1) в окрестности нулевого приближения. Суть алгоритма состоит в следующем.

Исходя из заданного нулевого приближения к (£) к искомому распределению коэффици- ента пьезопроводности линеаризуем уравнение

(1) в окрестности нулевого приближения:

А ° т = т - т ⁰

= { ^а ° ^т ' }-Ь   i J i

L ( rn , rend l (^)А к (^) d^ 3[к °(^)J2

к ( ^ ) = к ° ( ^ ) + А к ( ^ )

Это система линейных алгебраических уравнений относительно коэффициентов А к ( ^ ) , может быть представлено в матричной форме. Матричная запись (2) имеет вид:

A ( К ° ) А К = А ° т .

Метод последовательных приближений состоит в нахождении А К из (3), проверки качества результата К ¹ = К ° + А К и повторения при необходимости вычислений с новым нулевым приближением равным К ¹ . Процесс продолжается до получения удовлетворительного результата. Этот алгоритм подробно описан в работе [11]. Оператор, реализующий описанную схему в его матричном представлении будем записывать в форме:

A ^{- 1}( К ) т = К .

Отображение, следующеиз (1) ипозволяющее рассчитать поле времен т = { т } ; Т i = Т ( r n , r nd ) прихода экстремальных значений восстановления давления по системе пар скважин в зависимости от распределения коэффициента пьезопроводности обозначаем:

A ( К ) = т .                 (5)

Оператор A ^{- 1}( К ) т = К является приближенным обратным [12] к «прямому» оператору (5) и устанавливает способ обращения (5) с целью расчета матрицы коэффициентов пьезопроводности К по наблюдаемым интервальным временам ^т = { т } ; Т = ^Т ( r n , г^ ) .

ГРАФОВОЕ ПРЕДСТАВЛЕНИЕ ПОТОКА ИНФОРМАЦИИ

Оператор (5) определяет взаимосвязь параметров из элементов матрицы К и параметров матрицы наблюдаемых т. Граф, связывающий каждый элемент из К с каждым элементом из т, оснащен весами для ребер, определяющими «коэффициент передачи» данных от элемента Ку к Ti. Это информационный граф оператора. Для линейных операторов A = { aijn }; A ( К )» ^ aijn Ky = Ti, роль jn весов играют элементы матрицы aijn . Пример изображения информационного графа приведен на рис. 1. По сути это тот же оператор A в его графическом представлении. Изображение информационного графа оператора распространяется и на случай нелинейных операторов, однако удобно рассматривать линейные приближения, для которых информационный граф более нагляден.

Пользуясь информационным графом для оператора (4) легко представить схемы передачи информации от компонент наблюдаемых интервальных времен к компонентам определяемой матрицы коэффициентов пьезопроводности. В качестве переносимых информационным графом параметров могут служить и характеристики наблюдаемых. Если для линейных операторов в качестве значений пере-

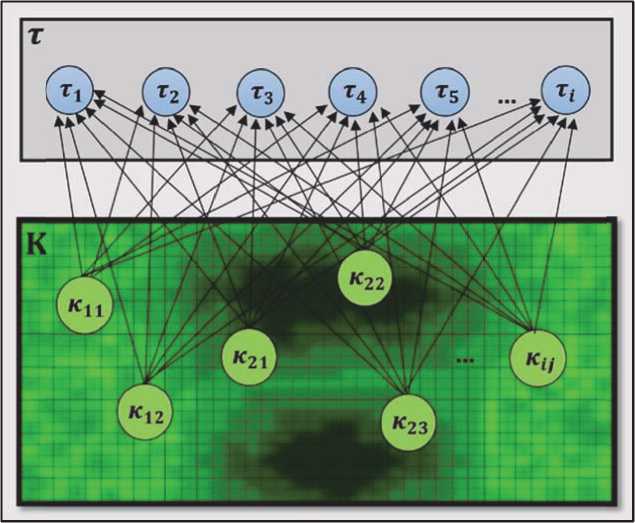
Рис. 1. Информационный граф оператора

носимых параметров будут выбраны величины интервалов доверия к наблюдаемым, то следует ожидать получения в качестве результата переноса интервалы доверия для итоговых определяемых параметров. Следует особо подчеркнуть, что оценки интервалов доверия корректны только в рамках модельных представлений, лежащих в основе конструирования оператора A и не являются интервалами доверия в общем случае. Изменение модельных представлений ведет к изменению конструкции оператора A , и как следствие, изменению вычисляемых интервалов доверия. В случае нелинейного оператора, к числу которых относится (4) отделение интервалов доверия от исходных данных неправомерно. Для определения интервалов доверия к определяемым параметрам – коэффициентам пьезопроводности в рамках сконструированной модели, следует определить параметры с переносимыми данными в верхней границе интервала доверия, повторить процедуру с данными соответствующими нижней границе интервала доверия и рассмотреть их разность.

Алгоритм нахождения интервалов доверия для коэффициента пьезопроводности заключается в следующем.

Для данных т определяется матрица доверительных интервалов Ат = { А т _г -} (не путать с промежуточными вычислениями А ° Т в (2)) и конструируются два набора входных параметров:

тsup = т + Ат = {ri + Ari); тinf = т - Ат = {ri - Ari}.

Далее по алгоритму, реализующему опе- ратор (4), определяются матрицы параметров

K ^sup и K ^inf

соответствующие решениям урав- sup inf нения (4) с данными т и т соответственно.

Интервал доверия рассчитывается по правилу:

AK = Ksup - Kinf .        (7)

В роли интервала доверия ДК могут выступать соответствующие размерности данных атрибуты нечеткой меры [13] для исходных данных. Итогом вычислений будут служит атрибуты нечеткой меры для определяемых коэффициентов пьезопроводности.

РЕЗУЛЬТАТЫ

Рассмотрим в качестве примера тестовое месторождение (рис. 2), содержащее 28 скважин. Все скважины последовательно были рассмотрены в качестве источника депрессии на пласт, по которой были смоделированы интервальные времена отклика в соседних скважинах. Всего в томографическом эксперименте участвуют 756 пар скважин, для охвата большей площади месторождения: т = {т , , 1=1^756). В качестве нулевого приближения пространственного распределения коэффициента пьезопроводности выбрана однородная среда (к(^(х,у))=0,3). Цветовая легенда соответствует обратной нормированной эффективной величине коэффициента пьезопроводности с условной размерностью. Значения, близкие к 1, соответствуют зонам аномального фильтрационного сопротивления (низкое значение коэффициента пьезопроводности), а значения, близкие к нулю, – соответствуют высокопроницаемым зонам.

Рис. 2. Расположение скважин и сетка на месторождении с заданным нулевым приближение среды K

На первом шаге вычислительного алгоритма гидродинамической томографии были определены траектории движения депрессии (экстремальной точки восстановления давления) между парами скважин L⁰ и рассчитаны интервальные времена τ ⁰ для нулевого приближения среды K (рис. 3).

Итогом вычислений на первой итерации гидродинамической томографии является новое пространственное распределение коэффициента пьезопроводности K1 (рис. 4), которое будет использоваться в качестве начального приближения среды на второй итерации.

Финальный результат гидродинамической томографии проницаемого пласта нефтяного месторождения представлен на рис. 5. Решение о прекращении процесса гидродинамической томографии принимается на основании заключения о том, что отклонение экспериментальных интервальных времен τ и времен τ ⁿ , рассчитанных на итерации n, может считаться удовлетворительной.

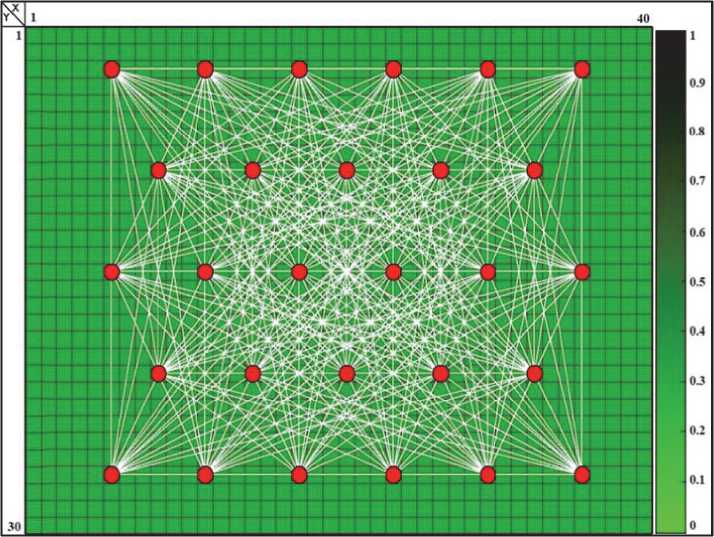
Рис. 3. Траектории движения экстремальной точки восстановления давления между парами скважин на первой итерации алгоритма гидродинамической томографии

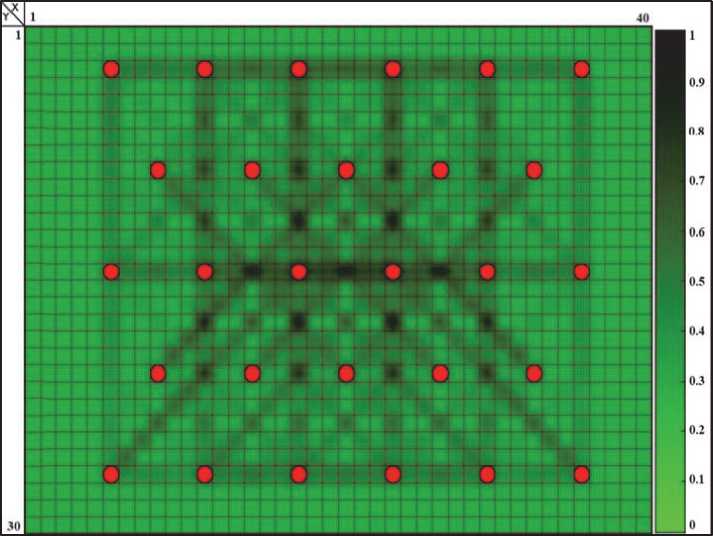
Рис. 4. Пространственное распределение коэффициента пьезопроводности после первой итерации алгоритма гидродинамической томографии K¹

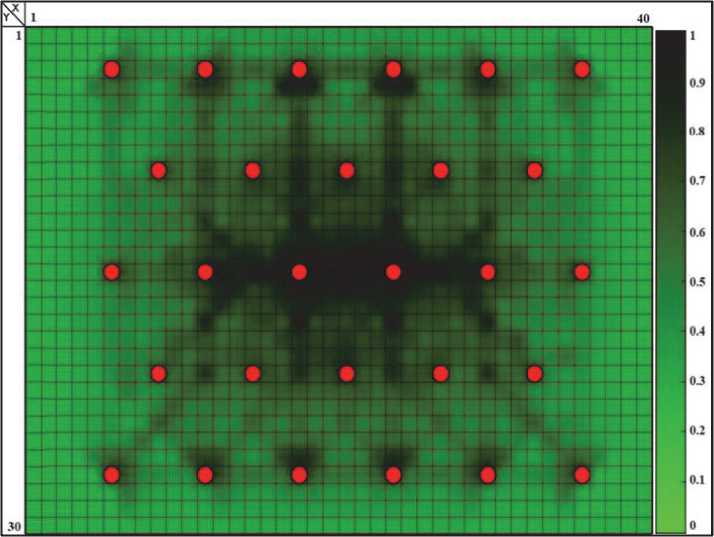
Рис. 5. Результат гидродинамической томографии проницаемого пласта

После решения задачи гидродинамической томографии для времен τ , конструируем новые наборы интервальных времен, включающие доверительные Δτ . Доверительный интервал времен τ был задан с уровнем 0,8 от интервального времени. Таким образом, разброс данных составлял 0,2 от значений интервального времени в каждой используемой для расчетов паре скважин. Верхняя и нижняя границы доверительного интервала с уровнем доверия 0,8 τ ^sup и τ ^inf определялись по формулам:

т ™р = т + (1 - 0,8) т;

тinf = т - (1 - 0,8) т.

Для каждого из набора времен τ ^sup и τ ^inf была решена задача гидродинамической томографии и получены соответствующие пространственные распределения коэффициента пьезопроводности K ^sup (рис. 6) и K ^inf (рис. 7) .

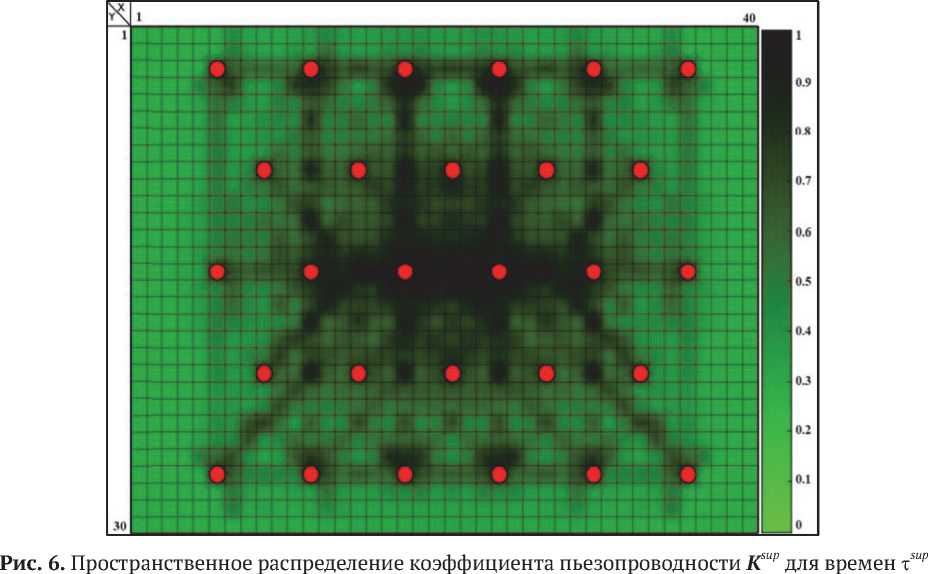
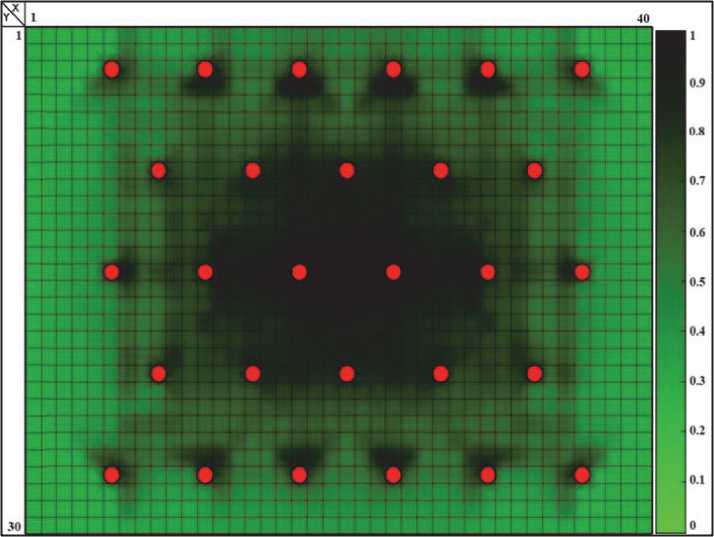
Рис. 7. Пространственное распределение коэффициента пьезопроводности K ^inf для времен τ ^inf

Интервал доверия Δ K (рис. 8) для распределения коэффициента пьезопроводности K между двумя решениями K ^sup и K ^inf рассчитывался по приведенному выше правилу (7). На краях сетки количество траекторий движения особой точки мало, в следствии чего в процессе расчетов эти участки мало изменялись относительно нулевого приближения, либо не изменялись вовсе. Именно с этим связаны пониженные значения интервала доверия. Это обстоятельство следует иметь в виду увязывая интервал доверия Δ K с плотностью сети траекторий (рис. 9) в соответствующих зонах модели.

Количество траекторий в ячейках сети нормировано относительно максимального значения.

ВЫВОДЫ

Построение пространственного распределения эффективного фильтрационного сопротивления основано на построении пространственного распределения коэффициента пьезопроводности методом гидродинамической томографии.

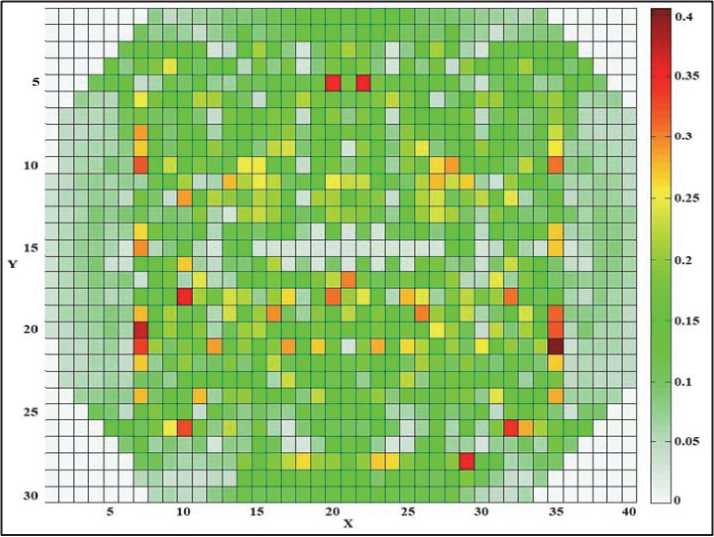
Рис. 8. Интервал доверия Δ K коэффициента пьезопроводности К

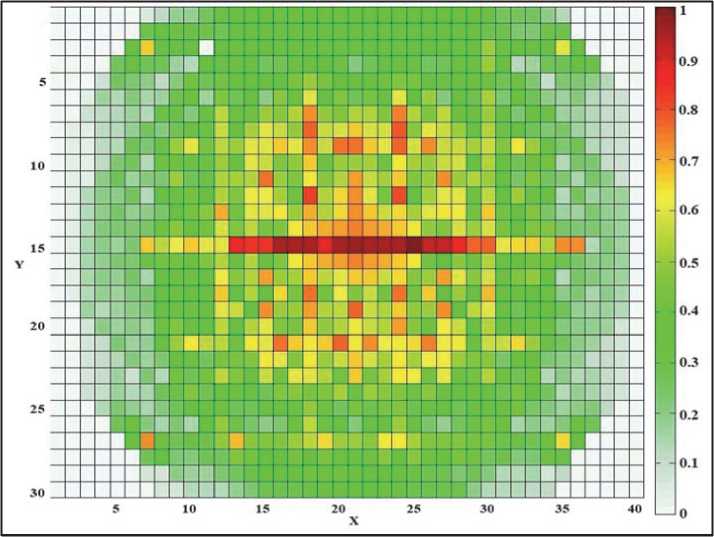
Рис. 9. Частота траекторий особой точки в ячейках сетки

Для оценки интервала доверия к результатам расчетов в методе гидродинамической томографии исходными данными служат интервальные оценки уровня доверия к интервальным временам движения возмущений между парами скважин, служащие входными данными в методе гидродинамической томографии.

На основании интервальных оценок уровня доверия формируются пакеты данных нижней и верхней границ интервалов входных данных. Пользуясь информационным графом оператора гидродинамической томографии и принципа- ми динамики нечетких мер для операторных уравнений, определяются нижние и верхние границы распределений коэффициента пьезопроводности, которые определяют искомые интервальные оценки. В вычислительном отношении это соответствует повторению расчетов для реализации схемы гидродинамической томографии с данными, соответствующими краевым интервалам используемых времен движения, возмущения между всеми парами скважин.

Приведенные вычислительные расчеты демонстрируют эффективность описанного алгоритма.