Инвариантная мера для одного класса кусочно-монотонных эндоморфизмов с квазиинвариантной мерой

n →∞ n →∞ k ₌0

Пусть (M, F, p) — пространство Лебега, то есть можно считать, что это отрезок [0, 1) с мерой Лебега. Эндоморфизм Т пространства M есть измеримое преобразование пространства M , при котором любая точка может иметь прообразом не одну точку, а любое конечное или счетное число, и даже континуум, точек, но меры 0.

В работе рассматриваются эндоморфизмы с квазиинвариантной мерой, то есть такие, что p(T ^-1 А) = р(А) .

Одним из интересных вопросов изучения таких эндоморфизмов является изучение существования инвариантной меры р , абсолютно непрерывной относительно меры Лебега р , то есть такой, что V A Е F р(Т ^-1 А) = р(А) .

Существование инвариантных мер довольно хорошо исследовано (см., например, [1; 2]). Однако построение инвариантных мер, начатое еще Гауссом, встречается довольно редко, но воспринимается с интересом.

Рассмотрим эндоморфизм Т : M ^ M , заданный формулой

	' 4x, 4(x - 1/4)+ 1/4,	0 6 x < 1/4, 1/4 6 x < 3/8,
	4(x - 3/8) + 1/4,	3/8 6 x < 1/2,
lX — \	4(x - 1/2) + 1/4,	1/2 6 x < 5/8,
	4(x - 5/8) + 1/4,	5/8 6 x < 3/4,
	1 4 (x - 3/4),	3/4 6 x < 1.

Этот эндоморфизм не сохраняет меру. Действительно, если А = [1/4, 3/4) , то р(А) = 1/2 = р(Т ^-1 А) = 3/4 .

Легко видеть, что р(Т ⁿ A) = 1/2 V n .

Разобьем  отрезок [0, 1)   на множества A 1 = [0,1/4) ,   A 2 = [1/4,3/4) ,

A3 = [3/4,1), а Ai1, i1 = 1, 3, на множества Ai1 i2 так, чтобы ТAi1 i2 = Ai1. То есть получим: An = [0, 1/16), A12 = [1/16, 3/16), A13 = [3/16, 1/4), A21 = [1/4, 3/8), A22 = [3/8, 1/2), A23 = [1/2, 5/6), A24 = [5/8, 3/4), A31 = [3/4, 13/16), A32 = [13/16, 15/16), A33 = [15/16, 1); Am = [0, 1/64) и т. д. Строим множества Aii,i2,...,in, n = 1, то, так чтобы Т Aii i2.„in = Ai^...^-.

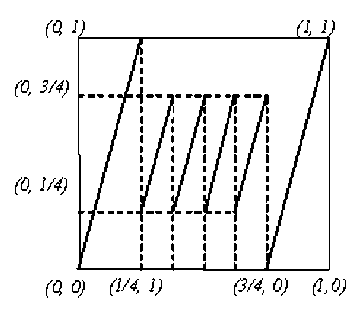
Рис. 1. Эндоморфизм T с квазиинвариантной мерой n-1

Определим меры ^n(B) = 1 ^ р(Т-kB) VB E F. Тогда д = lim цп есть инвари-n k=0                             n→∞ антная мера [1]. Применим лемму (см. [1, стр. 159]).

Лемма. Пусть T — произвольное кусочно-монотонное преобразование интервала [0, 1) . Если существует такая константа K > 0 , что р(Т - n A) 6 Kp(A), n = 1, то , для любого борелевского A С [0, 1) , то у преобразования Т имеется инвариантная нормированная борелевская мера µ , абсолютно непрерывная относительно р и такая, что d^ 6 K.

Легко видно, что р(Т n A) 6 Kp(A) V n и V A E F при K = 2 . Тогда существует мера р = lim p n . V B С A имеем р(Т ^-1 B) = p(B) + 1/2 p(B) и р(Т ^{- n} B) = p(B) + 1/2 р(Б) + 1/4 p(B) + ... + 1/2 ⁿ p(B) .

Так как V k при n > k  р(Т ⁿ B ) >   ( 2 — 1 / 2 ^k ) p(A) , то p(B) = 2p(B) =

= р(Т ^-1 B) . В частности, p(A) = 1 .

Если B С CA , CA — дополнение множества A , то р(Т ^-1 B) = 1/2 p(B) , р(Т ^{- n} B) = 1/2 ⁿ p(B) . Таким образом, p(B) = lim ¹ P £p(B) = lim ¹ 2p(B) = 0 .

n →∞ ⁿ _{i =0} ²         n →∞ ⁿ

Следовательно, инвариантная мера получается сосредоточенной на отрезке [1/4, 3/4), но с удвоенной плотностью; на отрезках [0, 1/4) и [3/4, 1) она имеет плотность 0. Мы получили, что этот эндоморфизм с инвариантной мерой изоморфен эндоморфизму Тх = 4х( mod 1). Известно, что это точный эндоморфизм, то есть lim р(ТnA) = 1 VA E F с p(A) > 0. Мы установили, что lim р(ТnA) = 1/2, где p(A) = 1/2. Это пока-n→∞ зывает, что точность эндоморфизма T с инвариантной мерой не может быть установлена с помощью равенства lim р(ТnA) = 1 VA E F с ^(A) > 0.

n →∞

Очевидно, что если взять любой кусочно-монотонный эндоморфизм, сосредоточенный на отрезке [1/4, 3/4) и сохраняющий на нем меру, на отрезке [0, 1/4) заданный функцией f i (x) с f i (0) = 0 , f i (1/4) = 1 , f l (х) >  а >  2 V x E [0, 1/4) ; f 2 (x) с f 2 (3/4) = 0 , f 2 (1) = 1 , f 2 (x) > в > 2 V x E [3/4, 1) .

Например, если взять эндоморфизм T такой, что

/

Tx = <

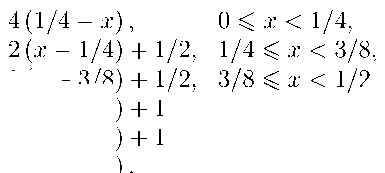
4(1/4 - x) ,

0 6 x < 1/4,

1/4 6 x < 3/8 3/8 6 x < 1/2 1/2 6 x < 5/8 5/8 6 x < 3/4 3/4 6 x < 1.

2 (x - 1/4) + 1/2 2(x - 3/8) + 1/2 2(x - 1/2) + 1/4 2(x - 5/8) + 1/4 4 (x - 3/4),

Рассуждая как в основном построении, получаем, что при том же самом преобразовании T с инвариантной мерой имеет вид

Tx =

2x + 1/2,

0 6 x < 1/4,

2 (x - 1/4)+ 1/2,  1/4 6 x< 1/2,

2 (x - 1/2),

2 (x - 3/4),

1/2 6 x < 3/4, 3/4 6 x < 1.

Если A = [1/4, 3/4) , то p(T n A) = 1/2 , отсюда следует, что для эргодических от-

( П—1   ,   \

U TkA = 1 может k=0 J не выполняться.