Инвариантная статистика слабых сигналов

Проблема обнаружения и распознавания слабых сигналов в условиях сильного шума является важной в измерении, обработке и интерпретации наблюдаемых данных. В отличие от традиционных статистических методов решения проблемы предлагается альтернативный метод на основе статистических инвариантов, не зависящих от числа независимых событий в совокупности. Эти инварианты можно получить, разлагая моменты наблюдаемой совокупности в ряд по степеням ее дисперсии. Но проблема усложняется тем, что наблюдаемая совокупность есть смесь слабого сигнала и сильного шума. Обнаружить слабый сигнал на фоне сильного шума не так-то просто. Астрономы и фотографы ночных объектов обнаруживают этот сигнал за счет длительной временной экспозиции. Физики его обнаруживают за счет пространственной когерентно возбужденной совокупности частиц.

СТАТИСТИЧЕСКИЕ ИНВАРИАНТЫ

Пусть неделимая смесь (когерентный сигнал плюс шум) есть

X = X + X x = mx s + X x .        (1)

Здесь m — число когерентных сигналов x s , X _x — шум.

Наблюдаемая совокупность содержит n независимых смесей

n

X n = Z X .                (2)

i

Предполагаем, что можно наблюдать отдельно фон при отсутствии сигнала и смесь при его наличии. Задача состоит в том, что на основе этих двух наблюдений обнаружить и распознать сигнал.

В работе автора [1] разработана теория и технология решения таких задач. В основе этой теории лежат статистические инварианты. Они строятся на моментах разных порядков. Для наблюдаемой совокупности имеем:

X„ = nX , D = nD , G_n = D / X ", nnnnn

X = J 1 D n , X „ ⁴ = J 2 D n + 3 D „ ²,

J 3 = X V D n - 10 J 1 D n ,                      ⁽³⁾

J ₄ = X „ ⁶/ D n - (15 J 2 + 10 J 2 ) D n - 15 D 2

Здесь X _n , D_n — среднее значение и дисперсия наблюдаемой совокупности; G_n — диссипативный инвариант; J_k ( к >  1) — статистические инварианты.

Эти зависимости позволяют непосредственно вычислить статистические инварианты:

Gn = Dn I X ,

J 1 = X n ³/ D n , J 2 = X n ⁴/ D n -3 D n ,

J з = X 5 / D n - 10 J 1 D n ,                     (4)

J 4 = X n ⁶/ D n - (15 J 2 + 10 J 2 ) D n - 15 D 2 .

Здесь Xk — к -й центральный момент наблюдаемой совокупности ( к > 2).

Коль скоро инварианты не зависят от n , получаем:

G = D / X ,

J ₁ = X ³/ D , J ₂ = X ⁴/ D - 3 D ,

J ₃ = X ⁵/ D - 10 J ₁ D ,                         ⁽⁵⁾

J ₄ = X ⁶ / D - (15 J ₂ + 10 J ² ) D - 15 D ² .

Здесь X ^k ( к >  2) — моменты неделимой части наблюдаемой совокупности; X , D — ее среднее значение и дисперсия.

Дисперсионный момент неделимой части наблюдаемой совокупности определяется из соотношений:

D ³ - А 1 D ² + А₂D - А ₃ = 0,

A = 2( J ² - J 2 ),

A = 2( J ₄ - J 2 ) + 9( J 2 - J ,⁴ ) +

12 J 1 ( J 1 J ₂ - J ₃)

⁺        12       ’

А з =

( J з - J i J ₂) 2 - ( J 2 - J 4 )( J 2 - J 2 ) 12

0 <  D <  D n .

Аналогичные соотношения можно получить для фона, предполагая, что ( X x = 0 ) :

J i x = x 3 / D x , J 2 x = x⁴J D x - 3 D x ,

J з x = X x / D x - 10 J 1 Д ,

J 4 x = X x / D x - (15 J 2 x + 10 J i² x ) D x - 15 D x .

Это позволяет найти дисперсию неделимой части фона из соотношений

D x - А 1 D x + A D_x - А ₃ = 0,

A = 2( J^ - J 2 x ),

_ [ 2( J 4 x - J 2 x ) + 9( J 2 x

-

. [ 12 J 1 ( J 1 x J 2 x - J 3 x ) ]

12           ’

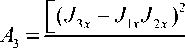
- ( J 2 x - J 4 x )( J 2 x - J 2 x ) ]

xnx

После изложенного можно выйти на обнаружение сигнала и на определение его инвариантной структуры.

Исходным является соотношение (1)

X = mX s + X_x .

Коль скоро фон центрирован, то его среднее значение

X _x = 0.

Для средних значений получаем:

X = m X s + X _x ,   X _x = 0,

X = m X s .

Меняя масштаб когеренции (экспозиции), находим

AX I A m = X s , m = X I X s .          (9)

С ростом когерентности (экспозиции) m среднее значение фона падает вплот ь до нуля, тогда как среднее значение сигнала m X s растет. После некоторой критической экспозиции, когда

(mX >> Xx)> сигнал будет устойчиво наблюдаться. Можно показать, что инварианты сигнала с ростом экспозиции растут:

J mks = mJ ,                (10)

где J_mks , J ks — k -й инвариант когерентной совокупности сигналов и одного сигнала соответственно.

ОБНАРУЖЕНИЕ СИГНАЛА

Если сигнал постоянный, то уравнения (9) позволяют обнаружить сигнал X s и его когерентный масштаб (экспозицию) m . Если сигнал имеет частотную структуру, то изложенные зависимости позволяют найти инварианты сигнала из структуры наблюдаемой совокупности и фона.

Покажем, как это можно сделать. Для начала рассмотрим дисперсию неделимой части смешанного сигнала в центральной системе координат:

X = mX s + X_x ,

< X >= 0, <  X_x >= 0, <  X s >= 0;

(здесь угловые скобки < > обозначают средние значения)

D = X ² = ( mX_s + X x ) ² = m ² D s + D x ,      (11)

d D I d m = 2 mD s , d ² D / d m ² = 2 D s .       (12)

Варьируя число когерентных частиц (экспозицию), можно найти дисперсию слабого сигнала D s , даже если дисперсия фона D_x очень высока. Сопоставляя (11) с (8), находим диссипативный инвариант

Gs = Ds IXs.(13)

Но с другой стороны имеем

G = DIX = (m2 Ds + Dx)/(mXs + Xx).(14)

При больших экспозициях

Xx = 0, X = mXs.(15)

В этом случае получаем

G = mGs + (1/m)Dx IXs.(16)

Минимальное значение диссипативного инварианта, а следовательно, максимальная организованность смеси получается при условии дG/дm = 0, Gs = (1 - m2)Dx ITs = 0.     (17)

Откуда находим m2 = Dx I Ds, m = V Dx/Ds.       (18)

Это наилучшее значение когерентных частиц (экспозиции). Чем больше дисперсия шума D_x по сравнению с дисперсией сигнала D s , тем больше должна быть экспозиция для обнаружения сигнала.

Для третьих центральных моментов имеем:

X ³ = J 1 D = ( mX s + X_x ) ³ = m ³ X s + X x =

= m ³ J , s D s + J , x D x .                           (19)

Отсюда находим инвариант J _{1 s} сигнала, зная инварианты смеси и фона.

Для четвертых моментов получаем:

X ⁴ = J ₂ D + 3 D ² = ( mX_s + X x ) ⁴ = = m ⁴ X s + 6 m ² D_sD_x + X ⁴, J ₂ D + 3 D ² = m ⁴ ( J _{2 s}D_s + 3 D ²) + + 6 m ² D s D x + J _{2 x}D_x + 3 D ².

Отсюда находится инвариант J _{2 s} .

Пятый момент раскрывается аналогичным образом:

X ⁵ = ( mX s + X x ) ⁵ = m ⁵ ( J 3 _sD_s + 10 J 1 _sD ²) + + 6 m ³ J 1 _sD_sD_x + 4 m ² J 1 _xD_sD_x + J 3 _xD_x + 10 J 1 _xD ². (21)

Это позволяет найти инвариант ( J 3 s ).

Наконец, для шестого центрального момента находим

X ⁶ = ( mX s + X x ) ⁶ = m ⁶ X 6 + 15 m ⁴ X s X x +

+ 20 m ³ X 3 X x + 15 m ² X s X x + X x .        (22)

Выразим моменты через инварианты:

X ⁶ = J ₄ D + (15 J ₂ + 10 J ²) D ² + 15 D ³ ,

X x 6 = J 4 x D x + (15 J 2 x + 10 J 2 ) D x + 15 D x , X s ⁶ = J 4 s D s + (15 J 2 s + 10 J 2 s ) D ² + 15 D 3 , X s ⁴ = J 2 s D s + 3 D s , X x = J 2 x D x + 3 D x ,

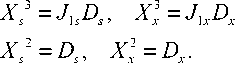
Такая система позволяет найти инвариант J _{4 s} . Итак, наблюдая когерентную экспозицию смеси

(сигнал плюс шум) и отдельно фон (шум), получаем инварианты смеси, инварианты сигнала и шума. Для этого необходимо наблюдать независимо друг от друга фон (шум) в случае отсутствия сигнала и смесь в случае его предполагаемого присутствия.

Такое разрешение проблемы смеси в рамках традиционной статистики практически невозможно.

РЕЗОНАНСНЫЕ СТАТИСТИЧЕСКИЕ СПЕКТРЫ

Но имея такую информацию, в рамках инвариантной статистики можно получить резонансные спектры смеси сигнала и шума как для неделимого события, так и для наблюдаемой совокупности неделимых событий.

Для неделимого события следует решить функциональное уравнение

X ³ - S ₁ X ² + S ₂ X - S ₃ = 0,

S ₁ = ( J ₃ - J ₁ J ₂ + 6 J 1 D )/( J ₂ - J ² + 2 D ),    (24)

- S ₂ = J ₂ - J 1 S 1 + 3 D , S ₃ = ( J 1 - S ₁) D .

Корни этого уравнения

X = ( X 1 , X 3 , X 2 ), ( X 1 < X 3 < X 2 )

являются резонансами неделимого события. Вероятности возбуждения резонансов определяются по формулам:

P = ( D + X 2 X 3 )/ [ ( X 1 - X 2 )( X 1 - X 3 ) ] ,

P 2 = ( D + X 1 X 3 )/ [ ( X 2 - X 1 )( X 2 - X 3 ) ] ,   (25)

P 3 = ( D + X 1 X 2 )/ [ ( X 3 - X 1 )( X 3 - X 2 ) ] .

Аналогично проявляются резонансы фона (шума):

X x - S 1 x X ² + S 2 x X x - S 3 x = 0,

S 1 x = ( J 3 x - J 1 x J 2 x + 6 J 1 x D x )/( J 2 x - J 2 x + 2 D x ), (26)

- S 2 x = J 2 x - J 1 x S 1 x + 3 D x , S 3 x = ( J 1 x - S 1 x ) D x .

Корни этого функционального уравнения

X x = ( X 1 x , X 3 x , X 2 x ), ( X 1 x <  X 3 x <  X 2 x )

являются резонансами неделимого события шума. Вероятности их возбуждения будут равны

P x = ( D x + X 2 x X 3 x )/ [ ( X 1 x - X 2 x )( X 1 x - X 3 x ) ] ,

P 2 x = ( D x + X 1 x X 3 x )/ [ ( X 2 x - X 1 x )( X 2 x - X 3 x ) ] , (27) P 3 x = ( D x + X 1 x X 2 x )/ [ ( X 3 x - X 1 x )( X 3 x - X 2 x ) ] .

Напомним, что эти распределения получаются при независимом наблюдении смеси и шума, при- чем число неделимых событий в наблюдаемой совокупности определяется соотношением n = Dn ID .

Резонансные спектры неделимого сигнала определяются из функционального уравнения

X - s _Sx s + s 2 _SX_S - s 3 s = o,

S 1 s = ( J 3 s - J 1 s J 2 s + 6 J 1 s D s M J 2 s — J 12 s + 2 D s ),   (29)

- S 2 = J 2 s - J 1 s S 1 s + 3 D s , S 3 s = ( J 1 s - S 1 s ) D s .

Корни этого уравнения

X s = ( X 1 s , X 3 s , X 2 s ), ( X 1 s ^ X 3 s ^ X 2 s )

являются искомыми резонансами неделимого события сигнала. Вероятности возбуждения этих резонансов равны

P s = ( D s + X 2 s X 3 s )I [ ( X 1 s - X 2 s )( X 1 s - X 3 s ) ] , P 2 s = ( D s + X 1 s X 3 s )I [ ( X 2 s - X 1 s )( X 2 s - X 3 s ) ] ,  (30)

P 3 s = ( D s + X 1 s X 2 s )I [ ( X 3 s - X 1 s )( X 3 s - X 2 s ) ] .

Наблюдаемая совокупность событий рассматривается в виде смеси резонансов неделимых событий:

X, = nX + nX. + nx , k 11   3  3   22

^Xkx = n 1 ^X 1 x ^{+ n} 3 ^X 3 x ⁺ n 2 x 2 x ,

^Xks = n 1 ^X 1 s ⁺ n 3 ^X 3 s ⁺ n 2 x 2 s , n_k = ( n 1 , n ₃, n ₂),    n 1 + n ₃ + n ₂ = n .

Число разбиений числа неделимых событий n на триады n k = ( n 1 , n 3 , n 2 ) равно

N = ( n + 1)( n + 2)I2.              (32)

Вероятности возбуждения каждой такой смеси (nk e N) равны n!

^k     n ₁! n ₃! n ₂!

^P 1 ^{n 1 P} 3 ^{n 3 P} 2 ^{n 2,}

n !

^kx     n ₁! n ₃! n ₂!

n !

n 1    n 3    n 2

^P 1 x ^P 3 x ^P 2 x ^,

^ks n ₁! n ₃! n ₂!

n 1    n 3    n 2

^P 1 s ^P 3 s ^P 2 s ^.

ЗАКЛЮЧЕНИЕ

Таким образом, проблема разделения наблюдаемой смеси на сигнал и шум, разрешена с помощью инвариантной статистики. Более того, ко- герентно-экспозиционное накопление сигнала в наблюдаемой смеси позволяет при определенной пороговой экспозиции не только обнаружить сигнал на фоне большого шума, но определить резонансные спектры распределения наблюдаемой смеси, сигнала и шума.

В рамках традиционной статистики такой результат получить практически невозможно. Например, в смеси отказов технических систем, состоящей из внезапного отказа и износа, разделение на распределения внезапных отказов и износов в общем распределении возможно в очень редких случаях при наличии гипотез о распределениях внезапных отказов и износа. В общем виде в рамках традиционной статистики такая задача неразрешима. При решении задач такого рода в полную меру проявляются преимущества инвариантной статистики.

Важным примером являются радиолокационное обнаружение объектов, теряющихся на фоне шума окружающей среды. Появляется возможность не только обнаружить объект, но и построить его резонансный спектр. Это позволяет распознать объект, отличить его от других по особенностям резонансного спектра.

Аналогичная ситуация возникает в гидроакустике. Сигнал объекта незаметен на фоновом шуме моря. Но наблюдая когерентную экспозицию сигнала смеси и отдельно фоновый шум моря, можно не только обнаружить объект, но и определить его резонансный спектр, который отличает обнаруженный объект от других. Это позволяет диагностировать и распознавать обнаруженный объект. Инвариантная статистика позволяет решать задачи подобного рода.

В Институте Ланжевена De Chiara u Palma проанализировали влияние шума на геометрическую фазу Берри частиц со спином ½. Они доказали, что с ростом экспозиции флуктуации фазы Берри падают — в пределе до нуля при больших временах экспозиции. Инвариантная статистика позволяет выделить фазу Берри при относительно малых экспозициях. Более того, она позволяет получить квантовый спектр фазы Берри, отделив его от спектра шума в наблюдаемой смеси. Такая возможность позволяет диагностировать квантовое состояние наблюдаемой физической среды.

Отметим исключительно важную особенность инвариантной статистики — она нелинейна. Это вызвано тем, что инварианты построены на статистических полиномах, которые позволяют учитывать групповые эффекты в наблюдаемой совокупности событий. В этом смысле статистические полиномы до шестого порядка включительно являются весьма информативными. Но инварианты не зависят от числа событий в наблюдаемой совокупности. Поэтому они несут "чистую" информацию о внутренней организации исследуемых про- цессов, что позволяет повысить разрешающую способность диагностики их состояния.

Важно, что резонансные спектры, построенные на инвариантах, являются индивидуальной характеристикой наблюдаемого процесса. Именно эта характеристика позволяет отличить одно состояние от другого и выделить статистические классы подобного состояния. На такой основе прекрасно выстраивается теория статистического подобия наблюдаемых процессов в дополнении к их геометрическому, физическому, аналоговому и алгоритмическому подобию.