Инвариантная завихренность и тепловое состояние ползущего течения жидкости сквозь проницаемую мембрану

Введение. Гидродинамика медленных («ползущих») течений вязкой жидкости имеет широкую область практических приложений [1]: химическая и мембранная технологии, фильтрация воды и нефти в грунтах, дисперсные системы и др. В теоретическом отношении наиболее полно изучены процессы медленного обтекания тел вращения, задачи о движении в жидкости групп из нескольких частиц, а также течение жидкости в пористой среде и вопросы гидродинамической теории смазки. Анализ современного состояния теории ползущих течений [2–5] показывает, что являются актуальными следующие вопросы: вихревые свойства течений при малых числах Рейнольдса, роль вязкой диссипации энергии в формировании структуры теплового поля жидкости, закономерности производства энтропии. Известно, что число Рейнольдса Re = ρ u_bl / µ представляет отношение сил инерции к силам вязкого трения и определяет интенсивность вынужденной конвекции. Здесь ρ – плотность жидкости; u_b – масштаб скорости; l – характерный линейный размер; ц - коэффициент динамической вязкости. Ползущее течение происходит при Re ^ 1, и это означает, что вязкость жидкости большая, а конвективное ускорение – малое. Следовательно, в уравнениях движения доминируют силы, зависящие от вязкости, и можно пренебречь инерционными членами. Движение жидкости мы рассматриваем с учетом внешней силы трения F = - ζ V , которая моделирует сопротивление потоку на границах области течения (стенки трубы, дно кюветы, подстилающая поверхность и др.) [6]. Здесь ζ – коэффициент сопротивления;

В настоящей статье изучаются гидродинамические и тепловые аспекты задачи о ползущем течении вязкой ньютоновской жидкости сквозь проницаемую мембрану. Цель работы: 1) получить новый класс двумерных стационарных ползущих течений вязкой жидкости с учетом внешней силы сопротивления; 2) построить в виде сильного гидродинамического разрыва математическую модель проницаемой мембранно-капсульной системы; 3) изучить вихревые, диссипативные и энтропийные свойства этого течения.

Точное решение. Стационарное ползущее течение жидкости определяется следующими уравнениями:

∂u ∂υ

+   =0,

∂x ∂y д и д и   дp    „

Ц ,. + ; =з^+Pzu, (дx   ду ) дx

∂ x

Механика

	µ	^д 2 U д 2 U ч д x 2 +д у 2 ,	= ∂ p + ρζυ , ∂ x
c	f д T    д T ) . u + υ   = λ ( д x     д у )		f д 2 т д 2 T ^ "^ + ^ д x     д у ^	+Ф ,

Φ= µ

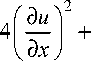
( ди д и f

+5" I

^ д x д у )

где x , y – прямоугольные декартовы координаты; p – давление жидкости; u , υ – компоненты вектора скорости V = и + и ; T - температура; X - коэффициент теплопроводности; c = p c p -объемная теплоемкость; Φ – диссипативная функция. Рассматриваем процессы, для которых ρ , µ , ζ , λ , c - const , и динамическую задачу решаем отдельно от тепловой. Производство энтропии за счет внутренних необратимых процессов подсчитывается по формуле [9]:

О = [( q ■ q )/( X T ² )] + ( Ф / T), (6) где q - вектор удельного теплового потока, имеющий компоненты, q_x = -Хд T / д x , q_y = -λ∂ T / ∂ y . Принцип минимума производства энтропии в стационарных состояниях (принцип Пригожина) выражается неравенством [10]:

σ stab ^≤ σ instab , (7) где левая/правая части неравенства соответствуют производству энтропии в устойчи-вом/неустойчивом состояниях. Для неравновесного перехода термодинамической системы из старого в новое состояние принцип (7) означает следующее: новому устойчивому состоянию отвечает меньшее значение производства энтропии, чем производство энтропии старого, но продолженного в неустойчивую область состояния системы. Подробное изложение этого вопроса и библиография проблемы даны в [10].

Непосредственной подстановкой можно убедиться, что уравнения гидродинамики (1)–(3) имеют следующее точное решение:

и = /Sn, и = S, (8) ξ= E sinδy , η= E cosδy , E = expδx , (9) / = d) / d^ = y1 + 3/3^2, /1,/3 - const, где ψ =ψ(ξ) – функция тока. Параметр решения δ удовлетворяет связи ζ = 8δ2ν, ν= µ/ρ . Давление жидкости подсчитывается по формуле

Π≡p-p0 =2µδ2E2ηψ3 - ρζ(ψ1η+ψ3ξ2η), p0 ≡const. (10) Завихренность течения равна to = (1/2)[(ди/дx)-(ди/ду)]^y/S1 E2/2, y) = 6y3q, (11) где ψ3 – свободный параметр. Компоненты девиатора тензора напряжений такие: τxx = -τyy = 2µ∂u/∂x , τxy =τyx = µ[(∂υ/∂x) + (∂u/∂y)] . Диссипативная функция (5) имеет вид:

Φ = 4 µδ ⁴ E ² [9 ψ ₃ ² E ⁴ sin ² δ y cos ² δ y + ( ψ ₁ + 6 ψ ₃ E ² sin ² δ y ) ² ] . (12) Плоскость течения разделена на две области. Область 1 – это правая полуплоскость x ≥ 0, δ ⁽¹⁾ = δ < 0 . Область 2 – это левая полуплоскость x ≤ 0, δ ⁽²⁾ = - δ ⁽¹⁾ = - δ > 0 . Верхний индекс в скобках указывает номер области. Принимая во внимание структуру формул (8)–(10), берем ψ ₁ ⁽¹⁾ =- ψ ₁ ⁽²⁾ = ψ ₁, ψ ₃ ⁽¹⁾ = - ψ ₃ ⁽²⁾ = ψ ₃ , ρ ⁽¹⁾ = ρ ⁽²⁾ = ρ , ζ ⁽¹⁾ = ζ ⁽²⁾ = ζ , µ ⁽¹⁾ = µ ⁽²⁾ = µ , p ₀ ⁽¹⁾ = p ₀ ⁽²⁾ = p ₀ , и тогда при одних и тех же значениях x получаем:

u ( x ≤ 0, y ) = u ( x ≥ 0, y ) ; υ ( x ≤ 0, y ) = - υ ( x ≥ 0, y ) ; (13)

Π ( x ≤ 0, y ) =-Π ( x ≥ 0, y ); τ _xx ( x ≤ 0, y ) =- τ _xx ( x ≥ 0, y ) ;

τxy(x≤0, y) =τxy(x ≥0, y); ω(x≤0, y)=ω(x≥0, y) , где y ∈ (-∞, ∞) . Из дальнейшего решения тепловой задачи будет ясно, что надо также взять λ(1)=λ(2)=λ, c(1)=c(2)=c.

Гидродинамическая интерпретация решения заключается в том, что проницаемую мембрану [линию x = 0 ] мы принимаем за неподвижный вдоль нормали / сильный разрыв. На таком разрыве должны быть выполнены динамические условия совместности [11], являющиеся следствием интегральных законов сохранения массы, импульсов и энергии. В данном случае имеем при x = 0 следующие условия:

ρ(1)u1 = ρ(2)u2 =ρu ;(14)

Т + p® - Р11VU1 = p<2 - р(2) У2u2 ;(15)

W + p^ ■ Vi - q® - p(1)ui [(V?2 /2) + Ui] = p<2 • V — qX2) — P(2)u2 [(V?22 /2) + U2],(16)

где p_n - вектор поверхностных напряжений с компонентами p_nx = - p + T _xx , p_ny = T _xy ; R ( R_x , R_y ) и W – поверхностные плотности распределения на разрыве внешних для жидкости возбуждающей силы и притока энергии. Индексами 1, 2 отмечены параметры течения справа ( x = + 0) и слева ( x = - 0) от разрыва. Далее все формулы записаны в терминах и обозначениях правой полуплоскости, x ≥ 0 .

Физические и физико-химические процессы на поверхности мембраны могут быть весьма разнообразными [12]. Источники импульсов R и энергии W моделируют возбуждающее динамическое и тепловое воздействие мембраны x = 0 на жидкость. Из выражений (8)–(10) [см. также группу формул (13)] ясно, что при x = 0 u -компонента скорости непрерывна, а υ -компонента меняет знак. Таким образом, при протекании через разрыв вектор скорости V сохраняет свой модуль, но изменяет направление, т.к. поворачивается на некоторый угол. Вязкое касательное напряжение τ _xy и диссипативная функция Φ непрерывны при x = 0 . Отклонение давления Π = p - p ₀ от его отсчетного значения p ₀ имеет разные знаки по обе стороны ( x = ± 0) разрыва. Вся плоскость течения разделена на полосы линиями δ y = π n ₀[ n ₀ = 0, ± 1, ± 2,… – любое целое число], вдоль которых υ = 0 , u = δ E ψ ₁( - 1) ^{n 0} . Значит, δ y = π n ₀ – это линии растекания потока (spread line), которые обладают еще и тем свойством, что вдоль них ω = 0, см. (11). При переходе через линию растекания υ -компонента скорости и завихренность ω меняют знаки. Характерные точки гидродинамического поля – это точки пересечения линии разрыва и линий растекания:

x = 0 , δ y = π n ₀ , υ = 0 , u = ψ ₁ δ ( - 1) ^{n 0} , Π = ( - 1) ^{n 0} ρζ [( ψ ₃ /4) - ψ ₁] .

Для краткости называем каждую такую точку s -точкой. В s -точке скорость непрерывна, а скачок давления [ Π ⁽¹⁾ = -Π ⁽²⁾ ] обусловлен действием возбуждающей силы R . Группа линий поворота

δ y = 2 π n ₀ ± ( π / 2) , u = 0 , υ = - ( ψ ₁ + 3 ψ ₃ E ² ) δ ( ± E ) , p = p ₀ представляет собой семейство изобар, и на каждой p ₀ -изобаре происходит поворот вектора скорости, потому что u -компонента меняет знак при переходе через p ₀ -изобару. Данное течение является периодическим по координате y , и наблюдается перемежаемость p ₀ -изобар (линий поворота) и линий растекания потока. Обсудим два режима движения жидкости: безвихревое течение по обе стороны проницаемой мембраны и вихревое течение, содержащее мембраннокапсульную систему.

Безвихревое течение. При ψ ₃ = 0 имеем нулевую завихренность ω ≡ 0, см. (11). Схема расположения векторов скорости жидкости дана на рис. 1. В каждой полосе между линиями растекания доминирующее направление движения показано дуговыми стрелками. В центральной части рис. 1 (вблизи оси ординат δ y ) тонкими стрелками указано изменение направления вектора скорости, являющееся результатом натекания жидкости на сильный разрыв. Отдельный отрезок на разрыве, например [ - π , 0] , [0, π ] , [ π , 2 π ] и т.д. является звеном всей цепочки x = 0 .

Механика

Из рис. 1 ясно, что каждое звено обтекается потоком жидкости и на краях звена, т.е. в s -точках, векторы скорости параллельны и противоположны друг другу. Из (15) находим:

x = 0, R_x = (9/4) Π , R_y = 2 ρ u υ ,                          (17)

где Π ( x = 0, y ) = - 8 δµ u ( x = 0, y ) . Для случая ψ ₃ = 0 гидродинамическое поле (8)–(10) есть результат действия двумерного источника импульсов (17). На разрыве скорость и давление жидкости выражаются через компоненты возбуждающей силы следующим образом: Π = (4/9) R_x , u ² υ ² = R_y ² /(4 ρ ² ) , u ² + υ ² = δ ² ψ ₁ ² . Давление Π пропорционально поперечной к разрыву R_x -компоненте. Продольная по отношению к разрыву R_y -компонента силы нелинейным образом проявляет себя при формировании двумерного гидродинамического поля, а именно: R_y мультипликативно связана со скоростями u , υ .

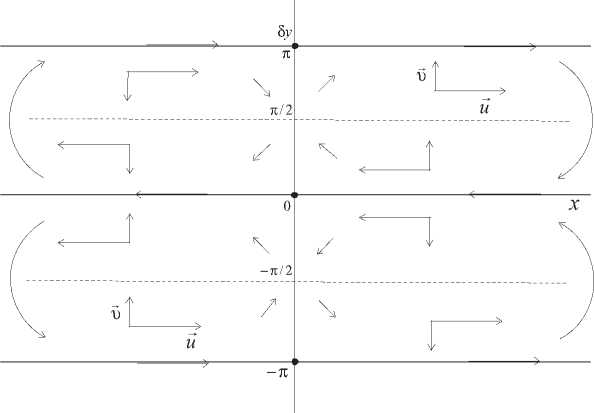
Рис. 1. Схема течения жидкости по обе стороны сильного разрыва. Толстые стрелки – компоненты вектора скорости; тонкие стрелки – направление вектора скорости вблизи разрыва. Линия растекания – сплошная; линия поворота – пунктирная. Дуговая стрелка указывает направление движения жидкости в полосе между линиями растекания. Темные кружки – s -точки

Уравнение энергии (4) имеет точное решение:

T - T 0 = θ 1 ξ - ( µ 1² ξ ² /2), µ 1² = (4 µ / λ ) δ ² ψ 1² , ψ 3 = 0,              (18)

где θ ₁ – произвольная постоянная; T ₀ – отсчетное значение температуры. Безразмерный критерий µ ₁ ² / T ₀ = 4Pr( u ² + υ ² ) /( c _pT ₀) , x = 0 несет информацию о числе Прандтля Pr = c_p µ / λ и об отношении двух характерных плотностей энергии: кинетической ρ ( u ² + υ ² )/2 и тепловой ρ c_pT ₀ . Своеобразие решения (18) в том, что для него сумма конвективных членов в уравнении (4) обращается в нуль тождественно. Взяв T ₀ ⁽¹⁾ = T ₀ ⁽²⁾ = T ₀ , θ ₁ ⁽¹⁾ = - θ ₁ ⁽²⁾ = θ ₁ >  0 , получаем, что при x = 0 непрерывны температура и касательная к разрыву составляющая теплового потока q ⁽ _y ¹⁾ = q ⁽ _y ²⁾ ; см. также (13). Нормальный к разрыву тепловой поток меняет знак при переходе через границу x = 0 : q ⁽ _x ¹⁾ = - q_x ⁽²⁾ . На основе соотношения (16) получаем:

W =- 2 λδ ( T - T ₀) - [5 u ² /( u ² + υ ² )]( Φ / δ ), x = 0.              (19)

Это значит, что возбуждающий источник энергии W расщепляется аддитивно на два тепловых потока: первое слагаемое в правой части (19) ассоциируется с переносом энергии за счет теплопроводности, второе слагаемое относится к вязкой диссипации энергии. В s -точке имеем постоянную температуру T = T ₀ и источник энергии W = - 5 λδµ ₁ ² >  0 ; тепловой поток направлен вдоль линии    разрыва:      q_x = 0 , q_y = - λδθ ₁ ( ± 1) ;     производство энтропии

σ = [ λδ ² θ ₁ ² / T ₀ ² ] + (4 µδ ² u ² / T ₀) экстремумов не имеет.

Точку пересечения линии разрыва x = 0 и изобары p = p ₀ назовем p ₀ -точкой. Здесь имеем два варианта: p ₀ ⁺ и p ₀ ^- различаются знаками sin δ y = ± 1 . Тепловое состояние этих точек определяется выражениями:

T - T 0 =± θ 1 - ( µ 1² /2), W =- 2 λδ ( T - T 0 ), и так же, как в s -точке, производство энтропии обладает свойствами монотонности ∂ σ / ∂ ( µ ₁ ² ) >  0 , ∂ σ / ∂ ( δ ² ) >  0 . Для θ ₁ >  0 и θ ₁ <  0 решение имеет одно и то же физическое содержание. При T = T ₀ + µ ₁ ² + ( µ ₁ ⁴ /4 T ₀) производство энтропии σ = σ ( θ ₁) достигает минимального значения σ _min ( θ ₁) . При положительном/отрицательном θ ₁ этот минимум наблюдается в p ₀ ⁺ / p ₀ ^- точке. Режим функционирования p ₀ ^± -точки, соответствующий σ _min ( θ ₁) , осуществляется при ϕ ≡ λ ( T - T ₀) δ ² / Φ = 1 + ( µ ₁ ² /4 T ₀) , т.е. в значительной степени зависит от числа Pr . Согласно (7), это значение ϕ определяет нижнюю границу производства энтропии для устойчивых течений.

Мембранно-капсульная система. Рассмотрим решение (8) – (10) при ψ ₃ >  0 , ψ ₁ <  0 [напомним, что в левой полуплоскости нужно брать ψ ₃ <  0 , ψ ₁ >  0 ]. В этом случае существует неподвижная непроницаемая граница ξ _w ² = - ψ ₁ /(3 ψ ₃) >  0 ; ξ _w ⁽¹⁾ = - ξ _w ⁽²⁾ = ξ _w . Линия ξ = ξ _w определяет плоский двумерный контур капсулы exp δ x = ξ _w / sin δ y , причем в каждой полосе, ограниченной линиями растекания ξ = 0 , следует брать ξ _w с тем же знаком, что и sin δ y . Будем различать «большие» [ ξ _w ² = ε ∈ (0, 1)] и «малые» [ ξ _w ² = 1 - ε > 0] капсулы, где ε – малый положительный параметр. На линии поворота δ y = 2 π n ₀ ± ( π / 2) имеем exp δ x = ξ _w , и поэтому малым, но конечным значениям ξ _w ² соответствует «большая» капсула, вершина которой находится на большом, но конечном расстоянии от мембраны x = 0 . Вместе с тем, чем меньше ξ _w ² , тем ближе основание капсулы ( x = 0 ) к линиям растекания. Если ξ _w ² = 1 - ε , то непроницаемая граница «малой» капсулы локализована в конечной окрестности p ₀ -точки. Стыковка при x = 0 решений для левой и правой полуплоскостей дает излом линии контура капсулы (рис. 2). Точки излома – это точки соединения основания капсулы с мембраной. В итоге имеем мембранно-капсульную систему (0 < ξ _w ² <  1) , в которой отдельные проницаемые участки мембраны соединены неподвижными непроницаемыми капсулами. Решение (8)–(10) имеет физический смысл во внешней для капсул плоской двумерной области: 0 ≤ ξ ² ≤ ξ _w ² . Схема течения показана на рис. 2. На стенках капсулы выполнены условия прилипания и непротекания.

Завихренность течения определяется формулой (11) и не зависит от константы ψ ₁ , являющейся параметром формы капсулы. Значит, конечные возмущения скорости и давления, которые характеризуются слагаемыми, содержащими ψ ₁ [см. (8)–(10)], оставляют без изменения вихрь скорости. Таким образом, в данном классе решений для данного типа конечных возмущений наблюдается инвариантная завихренность ползущего течения вязкой жидкости. Кривизна вершины капсулы равна K = δ , т.е. коэффициент сопротивления можно записать в виде ζ = 8 K ² ν . На вершине капсулы [sin δ y = 1, E = ξ _w ] имеем зависимости

ω ² = 9 K ⁴ ψ ₃ ² ξ _w ⁶ , Φ = 4 µω ² ,                           (20)

которые указывают на важную роль кривизны K в формировании вихревого поля.

При решении тепловой задачи учитываем вязкую диссипацию энергии, а конвективными членами в левой части уравнения энергии (4) пренебрегаем, полагая, что Pe = RePr <<  1 , где Pe = lu_b /( λ / c ) – число Пекле. Тепловое состояние жидкости определяется следующим выражением:

T - T 0 = θ 0 ( ξ ) + E ² θ 2 ( ξ ) , θ ₀( ξ ) = ( ξ / ξ _w )( θ _w + µ ₄ ² ) - ( µ ₁ ² ξ ² /2) + µ ₁₃ ξ ⁴ - µ ₃ ² ξ ³ [ ξ _w ³ + (2 ξ ³ /5)],

Механика

θ ₂( ξ ) = (3 µ ₃ ² ξ /4)( ξ _w ³ - ξ ³ ), µ ₁ ² = 4 µδ ² ψ ₁ ² / λ , µ ₃ ² = 4 µδ ² ψ ₃ ² / λ , µ ₁₃ = - 4 µδ ² ψ ₁ ψ ₃ / λ , µ ₄ ² = - 58 µδ ² ψ ₁ ³ /(135 λψ ₃) .

δ y

π

- u

(           ( I ul \

0 x

υ

-π

Рис. 2. Схема течения жидкости сквозь мембранно-капсульную систему. Обозначения такие же, как на рис. 1

Линия растекания ξ = 0 имеет температуру T = T ₀ >  0. Стенки капсул тоже изотермические: ξ = ξ w , T w = T 0 + θ w > 0 . Выбор произвольной постоянной θ _w определяет температуру капсулы. Если θ _w >  0 , то T_w >  T ₀ , и называем капсулу «горячей». Если θ _w <  0, то 0 <  T_w <  T ₀ , и называем капсулу «холодной». При протекании через мембрану температура жидкости непрерывна, а вектор теплового потока сохраняет свой модуль и поворачивается на некоторый угол, потому что меняет знак компонента q x = q ^¹ = - q X ²^. Вдоль линии растекания q x = 0 , и вектор q ортогонален этой линии. На вершине капсулы тепловой поток ортогонален мембране: q_y = 0 . На мембране возбуждающие источники импульсов и энергии имеют вид:

x = 0 , R_x = D Π , R_y = 2 ρ u υ ,

D = (2 + 27 ξ w ² - 26sin ² δ y ) /(1 + 12 ξ w ² - 4sin ² δ y ),

W = 2( Π u - τ xx u - τ xy υ + q x ) .                             (21)

Для «большой» капсулы получаем простую формулу D ≅ 2 , т.е. нормальной к разрыву компоненте Rx ≅ 2Π соответствует удвоенный перепад давления Π = p - p0 . Для «малой» капсулы вблизи ее основания D ≅ 1/3 , а в s -точках D ≅ 29/13 > 2. Развернутая запись выражения W(y) не приводится. Отметим только, что у основания «большой» капсулы, т.е. вблизи s -точки, источник энергии генерирует завихренность: W = [-µω2 /(3δ)] + Ο(ε) . Для системы «малых» капсул источник энергии в s -точке генерирует кинетическую энергию на линии растекания: W = (-64 / 3)µδ2u 2 + Ο(ε) . Стенки «малой» капсулы располагаются в ε-окрестности p0 -точки, и здесь источник энергии W ≅ 2qx определяет нормальный к разрыву тепловой поток, а остальные слагаемые в (21) имеют по отношению к ε порядок малости не ниже первого.

Обсудим экстремальные свойства производства энтропии. Сначала рассмотрим σs -режим, который характеризуется тем, что в s -точке зависимость σ(ξw2) имеет минимум при условии, что

_Ф1, _ д т . - T 0 ) ^ ² = _± + 29 5 W

^{V w}      Ф 12   45 ^

351¹⁺x w )

+ 2 z ϕ ₀

1/2

где Φ = 9λδ2ξw4µ32 , ϕ0 = λT0δ2 /Φ , Tw - T0 =θw . Здесь учтено, что в s -точке q • q = ^^

Шабловский О.Н.

Знаки –/+ в (22) относится к «холодной»/«горячей» капсулам. Для «горячей» капсулы σ_s -режим существует при всех T₀> 0 , а для «холодной» стенки имеем ограничение ϕ₀> (12/5) , ξ_w²∈(0, 1) . Если капсула «большая», то допустимы меньшие значения ϕ₀ . Например, при ξ_w²=1/100 достаточно взять ϕ₀> 1/10 . Связь (22) определяет нижнюю границу производства энтропии в σ_s -режиме для устойчивых течений сквозь мембранно-капсульную систему.

Теплоизолированная $ -точка ( = 0) существует в режиме «холодной» стенки 0w< 0 (23) и при этом на вершине капсулы получаем ∂(ω²) /∂(ξ_w²) > 0 . Значит, с ростом размера «холодной» капсулы [∂(ξ_w²) < 0] модуль завихренности на вершине убывает. Чем больше кривизна вершины, тем больше вязкая диссипация энергии Φ ~ ω²~ K⁴(20).

Далее рассмотрим σ_K -режим, для которого на вершине «горячей» капсулы зависимость σ = σ(K ) имеет экстремум при условии, что

(χ-7)(21-χ)=72χ(Tw/θw), 7<χ<21.                   (24)

Безразмерный критерий χ= λθ_w /(µψ₃²ξ_w⁶K²) содержит параметр завихренности ψ₃², а также параметры ξ_w²и K , определяющие морфологические свойства капсулы (размер и кривизну). Ясно, что χ= 36ϕ_w, где ϕ_w = λ(T_w - T₀)δ²/Φ вычисляется на вершине капсулы. Расчеты показывают, что существует пороговое значение χ_∗ = 147 , разделяющее интервал (7, 21) на две части, для которых σ_K -режим (24) обладает двумя типами экстремумов производства энтропии. Если 7 <χ<χ_∗, то существует нижняя граница σ_min(K) . Если χ_∗<χ< 21 , то существует максимум σ_max (K ) – верхняя граница производства энтропии для устойчивых течений. Нетрудно видеть, что в пороговом состоянии χ_∗ = χ при заострении вершины капсулы нужно повышать температуру стенки T_w .

Заключение. Установлено, что существует класс стационарных ползущих течений, обладающих инвариантной завихренностью. А именно: указан определенный тип конечных возмущений скорости и давления, которые оставляют без изменения вихрь скорости. Обнаружена важная роль вязкой диссипации энергии при течении жидкости сквозь проницаемую мембраннокапсульную систему. Изучение σ_s и σ_K режимов [см. (22) и (24)] показало, что морфологические свойства капсулы оказывают значительное влияние на условия существования экстремумов производства энтропии.