Inverse Matrix using Gauss Elimination Method by OpenMP

Published Online February 2016 in MECS DOI: 10.5815/ijitcs.2016.02.05

• A. Gauss Elimination Algorithm

Gauss elimination is an algorithm involving elementary row operation in a matrix which is employed for numerous applications in linear algebra. Some of the applications of this method are: 1) Calculation of rank of a matrix 2) Solution of linear algebraic equations 3) Inversion of invertible matrix. In this paper, the computation is done using OpenMP. Analyzing the amount of time taken for deferent size of matrices. We are also concerned with measuring the speed up and efficiency in deferent cases.

The algorithm can be subdivided into two parts

• 1.    Forward Elimination: This process is used to convert the matrix into reduced row echelon form

• 2.    Backward Substitution: This process is uses reduced row echelon matrix to find the solution.

Calculation of inverse of an invertible matrix [A] is based on the fact that the matrix does not have more than one inverse.

Now consider a non-singular matrix A e R ^{n x n} as expressed below:

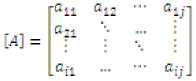
Then, in order to compute its inverse, we introduce an augmented matrix by adding an augmented matrix to the right of original matrix such that:

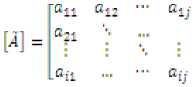
1   0    ...   o-

0    ■••    ...    0

0 ...... 1.

Suppose that the diagonal entry     is non-vanishing, then introducing a multiplier     such that:

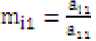
The elements under the first elements (a ) of original matrix A can be eliminated by multiplying each element of row-1 by m and then subtracting with the element of corresponding column from row-2 to final row. The mathematical operation can be written as:

ai; = ai; - m(1 x a1; i.j = 1.2.3 ...n Ьц = Ьц — т(1 x bLj t,j = 1,2,3 ...n b is the element in the right side of augmented matrix [Ã].

The resultant matrix after element row operation on 2nd row will take the following form:

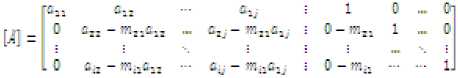
It can be observed that left side matrix has completely been transformed into identity matrix. so, the

corresponding right side matrix is the inverse of original matrix:

In the similar fashion, all the rows subsequent to row-1 can be modified by element row operation and elements below the diagonal elements can be eliminated. After the row operation for all the rows has been completed, the right side of augmented matrix takes the form of reduced row echelon as shown below:

b_L1 b₁₂ ... by b_?1 b_:2 ... by

.b^ b;₂ •" by.

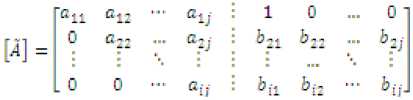
It can be seen that right side matrix of augmented matrix is no more an identity matrix. This completes the forward elimination process. The backward substitution process starts with the last row and goes upward until row-2. A multiplier is defined for each row and all rows above that row such that:

atk к = 1.2, ...я-1 a^ t = k + l,..... n

Elementary row operation is then preceded to eliminate all elements above the diagonal elements of right side of augmented matrix [Ã] :

B. Decomposition of the Matrix Problem

In this section we discussed how to start creating the parallel program. As we explained before we use a simple LU factorization method to factorize the matrix into lower triangular matrix and upper triangular matrix. These lower and upper triangular matrices are then used to calculate the inverse of the matrix. LU decomposition is done using Gaussian elimination method and involves less computation as compared to conventional matrix inversion technique.

Let us say that we need to invert matrix A. If B is the inverse of A, then:

.-i.S = 1                    (13)

Where, I is the identity matrix.

If we can break A into two matrices such that one is lower triangular matrix and the other is upper triangular matrix then:

«и = a₀- - m_ik x a_kj Ьц= b_tj-m_ik xb_kj

к = l,2,...n-l i,j = к + 1......n к = l,2,...n — 1 t, у = к +1,.....n

After completing the process upward for all the rows below row-1, the matrix takes the following form:

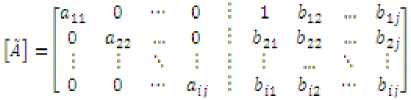
Each row is then divided by corresponding diagonal element of right matrix akk to make the right side matrix an identity matrix:

A = LU(14)

Where, L is lowering triangular and U is upper triangular matrix. Hence,

LU. В = 1(15)

:.e.L.m = 1(16)

(Where X = U.B)

We can solve the below two equations:

LX = J(17)

UB = X(18)

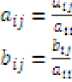
Hence the matrix takes following form:

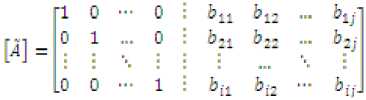
Solving the above two equations will yield as B, which is the inverse of A.

The computation of L and U can be parallelized as the computations do not depend on the previous steps. Similarly the computation of inverse can be parallelized, as the computation of each column of the result is independent of each other. The same logic is utilized for parallelizing the serial code using OpenMP directives.

C. OpenMP

OpenMP (Open Multiprocessing) is an API that supports multi-platform shared memory multiprocessing programming in C, C++, and Fortran, on most processor architectures and operating systems, including Solaris,

AIX, HP-UX, GNU/Linux, Mac OS X, and Windows platforms. It consists of a set of compiler directives, library routines, and environment variables that influence run-time behavior" (wikipedia). OpenMP is administered by the noncommercial technology society OpenMP Architecture Review Board, together explained by a group of major computer hardware and software vendors, such as IBM, Intel, Cray, HP, Fujitsu, Nvidia, NEC, Microsoft, Texas Instruments, Oracle Corporation, and so on. OpenMP involves a migratory, scalable model which grants programmers a simple and flexible interface for improving parallel applications for platforms ranging of the standard desktop computer to the supercomputer. OpenMP is an enforcement of multithreading, a process of parallelizing however the master thread (a category of directive completed consecutively) a specified number of slave threads and a task is separated all of them. The threads then run concurrently, with the runtime environment allocating threads to another processors.

The part of code which is proposed to run in parallel is marked as, with a preprocessor directive that will motive the threads to form before the part is accomplished. Each threads have an id related to it that can be acquired using a function (called omp_get_thread_num()). The thread id is an integer, and the master thread has an id of 0. After the enforcement of the parallelized code, the threads enter back into the master thread, whose continues onward to the end of the program. In general, each thread accomplishes the parallelized part of the code independently. Work-sharing constructs can be used to split a task all of it and the threads while all thread executes its allocated part of the code. Both tasks is similarity and data parallelism can be done using OpenMP in the same path.

• D.    Advantages Limitation and Features of OpenMP

There are some advantages of OpenMP such as the applications are relatively easy to implement and it is low latency and high bandwidth. So it also allows to run time scheduling and dynamic load balancing so the most advantage of OpenMP is the implicit communication [4] . Despite of all the benefits of OpenMP, there are some disadvantages such as parallel access to memory might decrease performance and also when the size of the parallel loop is too small the overheads can become an issue and explicit synchronization is required. The main features of OpenMp are as below:

• E.    Goals and Directives of OpenMP

There are some objectives of using OpenMP such as standardization, lean and mean, ease of use and portability. Each one has its own specifications. For standardization it provides a standard along with a diversity of shared memory architectures/platforms and together declared and allowed by a group of major computer hardware and software merchants. The other goal that create a simple and limited set of directives for programming shared memory machines and important parallelism can be implemented by using three or four directives called Lean and Mean [6]. Ease of Use provides ability to parallelize a serial program, not like message-passing libraries which typically involve an all or nothing approach and it provides the ability to implement parallelism for coarse-grain and fine-grain. In the last goal, which is the portability the API is only used for C/C++ and Fortran which is public forum for API and membership.

• • OpenMP directives utilize shared memory

parallelism by defining different types of parallel regions (table 1). Parallel regions can contain iterative and non-iterative parts of program code [8] .

Table 1. OpenMP Directives

#pragma omp	directivename	[clause, ...]	Newline
Compulsory for all OpenMP C & C++ directives.	A    usable OpenMP directive. Requirement implements after     the pragma and it also before all clauses.	Noncompulsor y. Clauses can be   in   any order,     and repeated    as important except    else classified.	Necessary. Precedes the arranged block that is enclosed  by this directive.

• II.    Performance Analysis

  This section investigates the illustrates of environment and the computer system information where the results from the proposed technique with IDE by Microsoft® Visual Studio 2010 Professional Edition and the application type is Win32 Console Application. So, the processor which used is Intel® Core™ i7- Q740 CPU @ 1.73 GHz with Microsoft Windows 7 Professional edition 64-bits operating system while the memory 4.00GB. the programming language e is C\C++. The following (table 2) illustrates the amount of time required of the computation of different size of matrices:

Table 2. Computation of Different Size of Matrix

Matrix size	1 Thread time	2 Threads time	4 Threads time	8 Threads time
500	35.077	25.316	20.373	12.475
1000	278.649	209.647	164.357	103.859
1500	943.088	692.289	518.232	309.041
2000	2046.7700	1554.950	1230.251	736.783
2500	3882.028	3113.930	2460.715	1523.236
3000	6416.146	5133.884	4053.464	2369.652

• A.    Efficiency & Speed Up

As it shown below from the tables and figures we compared the amount of time spent in all the computation using one thread, two threads, four threads, and eight threads. The computations were done for the different sizes of the matrices and the results are summarized in the table above. We can conclude that if we increase the number of threads the performance will be increased (less amount of time required). Also as the size of matrix increases, the efficiency of parallelization also increases, which is evident from the time difference between serial and parallel code. This is because, more computations are done parallel and hence the efficiency is high. The for loops are parallelized in a manner that blocks of matrices are decomposed by dividing the work among parallel threads.

• a.    In Fixed size of matrix and P is increasing Speed up is increased and Efficiency is decreased [9] .

Table 3. Case #1

N	1000	1000	1000
P	2	4	8
Speed Up	1.33	1.69	2.69
Efficiency	0.66	0.42	0.33

• b.    In increasing the size of matrix and P is fixed Speed up is decreased and Efficiency is decreased slowly.

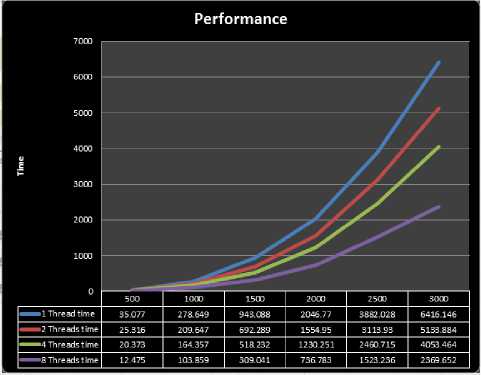
Fig.2. Dynamic Performance for Different Matrix Size

Table 4. Case #2

N	1000	2000	3000
P	4	4	4
Speed Up	1.69	1.67	1.58
Efficiency	0.42	0.41	0.39

• c.    In Fixed size of big matrix and P is increasing Speed up is increased and Efficiency is decreased.

Table 5. Case #3

N	3000	3000	3000
P	2	4	8
Speed Up	1.24	1.58	2.7
Efficiency	0.62	0.39	0.33

• B.    Schedule (type, chunk size)

In a static scheme and a specified chunk size, all processor is statically assigned chunk iterations. The distribution of iterations is completed at the beginning of the loop, and each thread will only accomplish these iterations assigned to it [10]. If using static with no a specified chunk size indicates the system default chunk size of n/p. Using a dynamic scheme, each thread is assigned a chunk of iterations at the beginning of the loop, so the exact set of iterations that are assigned to each thread is not recognized. The guided scheme gives a system dependent chunk of iterations among threads at the beginning of the loop. It is like to dynamic scheduling such that once a thread has done its work it is assigned a new chunk of iterations. The modification is that the new chunk size of iterations decreases exponentially as the iterations available decreases to a specified minimum chunk size. If the chunk size is NOT specified, the minimum is 1.

• C.    Behavior of the Schedule

For reduced values of N, all three schemes effort very well. With the dynamic scheme, the reduction in performance is greatly slower than it is with the others [11] . Since the amount of effort to be distributed is constantly changing during the algorithm, the dynamic scheme shows to work best because of its ability to distribute new iterations while other threads remain unavailable [12] . However as much as thread is getting executing static is performing better than dynamic and guided. For example in 8 threads static perform 30% better than dynamic and guided. While dynamic and guided perform better in 4 and 2 threads.

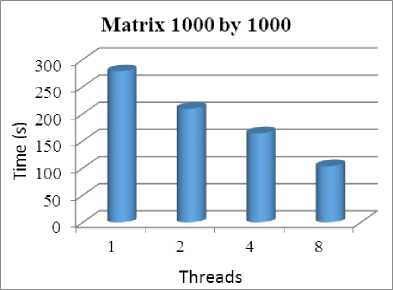
Fig.3.Computation for1000 by 1000 Matrix

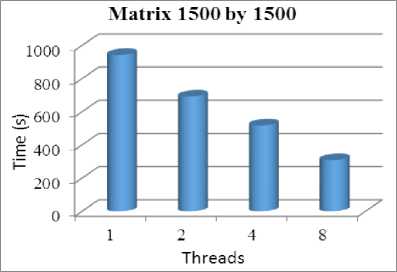
Fig.4.Computation for1500 by 1500 Matrix

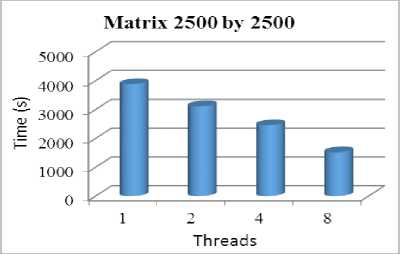
Fig.5.Computation for 2500 by 2500 Matrix

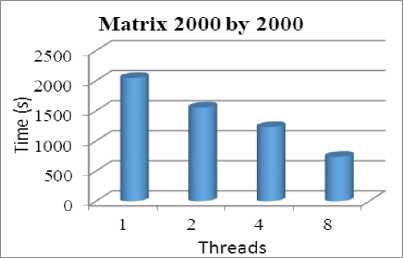
Fig.6.Computation for 2000 by 2000 Matrix

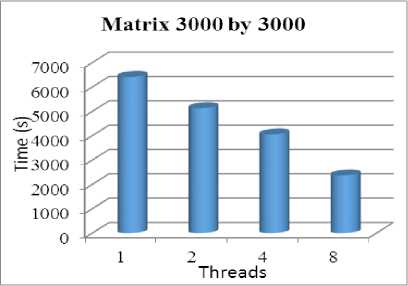
Fig.7.Computation for 3000 by 3000 Matrix

• III.    Conclusion

In summary, we have presented case which is inverse matrix using Gauss elimination method by openMP. After we fixed workload the decomposition was faster when more threads are executing in parallel. The execution was comparatively faster on larger workload due to the fact, parallelism was more effective. For a fixed number of cores the time increased exponentially with increase in matrix size. The parallelism was ineffective on relatively smaller loads. In Fixed size of matrix and P is increasing Speed up is increased and Efficiency is decreased. In increasing the size of matrix and P is fixed Speed up is decreased and Efficiency is decreased slowly. In Fixed size of big matrix and P is increasing Speed up is increased and Efficiency is decreased. In terms of the schedule’s behavior in 8 threads static perform 30% better than dynamic and guided. While dynamic and guided perform better in 4 and 2 threads.

Computational and Applied Mathematics, 236(3):326–341.

Acknowledgment

We wish to thank our families and friends for all support and concern. Both authors contributed equally to this work.