Investigating Performance of Various Natural Computing Algorithms

Published Online January 2017 in MECS

Nature is the best teacher. It has successfully provided extraordinary solutions to a large number of real-world complex problems by applying very simple approaches in systematic manners. This has attracted many researchers to mimic the nature in technology. As a result, natural computing has come up as a new era in the field of computing encompassing a broad range of applications. In the recent years, natural computing has established itself as an eminent force in finding promising solutions for complicated real world problems.

Natural computing algorithms are computer algorithms whose design draws inspiration from phenomena in the natural world [1]. These algorithms are also referred as nature-inspired algorithms, bio-inspired algorithms or clever algorithms. Two prime aspects of any natural computing algorithm are: exploration and exploitation [2]. Exploration refers to generating diverse solutions to explore search space as broadly as possible. It helps to avoid local minima. Exploitation refers to improving the quality of generated solutions by applying local search or other means. It strives to find the best solution. Natural computing algorithms work in an iterative manner by exploring and exploiting search space iteration by iteration to find optimal solutions.

The success of natural computing algorithms and their acceptance among researchers is mainly due to four factors as described in [3]. These algorithms are simple as they use simple concepts derived from nature. They are flexible and can be applied to different problems without major structural changes in the algorithm. They use derivation-free mechanisms and have abilities to avoid local optima (or, minima) . These features provide them superiority over traditional algorithms such as exact methods involving logical or mathematical programming.

Contrast to this, according to No Free Lunch (NFL) theorem [4], no single natural computing algorithm is best suited for solving all optimization problems. This has pushed researchers to develop new algorithms as well as to enhance existing algorithms. As a result, a number of various natural computing algorithms and their variations have been developed over the last couple of decades. These algorithms are summarized in next section.

This paper concentrates on some of the well known natural computing algorithms along with their variations such as Genetic Algorithm (GA), Ant Colony Optimization (ACO), River Formation Dynamics (RFD), Firefly Algorithm (FA) and Cuckoo Search (CS). The performance of these algorithms is investigated by applying them to the Traveling Salesman Problem (TSP)

which belongs to the class of NP-hard problems.

The remainder of this paper is organized as follows: Section II summarizes natural computing algorithms. Section III discusses the Traveling Salesman Problem along with its mathematical definition and associated complexity. Section IV describes various natural computing algorithms and their adaptations to solve TSP. Section V presents the detailed results of experiments conducted on a set of benchmark TSP instances given in TSPLIB library [5]. Finally, section VI provides conclusions based on comparative analysis of various algorithms.

• II.    Summary of Natural Computing Algorithms

This section summarizes various natural computing algorithms as given in table 1. Various algorithms are listed along with their abbreviations, inspirational natural phenomena, names of researchers and year of publication.

An honest attempt has been made in this section to provide state-of-the-art sum-up information on natural computing algorithms. This summary is aimed to provide readers a comprehensive list of all natural computing algorithms, developed in as early as the 1970s to recent ones, and to inspire them for further research.

Table 1. Natural Computing Algorithms – A Summary

Abbreviation	Algorithm	Underlying Natural Phenomena	Author(s)	Year	Reference(s)
GA	Genetic Algorithm	Natural selection process that mimics biological evolution	Holland	1973 1975 1992	[6]–[8]
SA	Simulated Annealing	Cooling process of molten metal	Kirkpatrick, Gelatt, Vecchi	1983 1997	[9], [10]
MA	Memetic Algorithm	Cultural revolution	Moscato	1989	[11]
ACO	Ant Colony Optimization	Foraging behavior of ants	Dorigo, Colorni	1991	[12]
GP	Genetic Programming	Extension of GA – Solution is represented as a tree with variable length	Koza	1992	[13]
PSO	Particle Swarm Optimization	Flocking behavior of birds	Kennedy, Eberhart	1995	[14]
DE	Differential Evolution	Genetic evolution with mutation as an arithmetic combination of individuals	Storn, Price	1997	[15]
BEA	Bacterial Evolutionary Algorithm	Microbial evolution phenomenon along with gene transfer operation	Nawa, Furuhashi	1999	[16]
AIS	Artificial Immune System	Human immune system	Dasgupta	1999 2003	[17][18]
ES	Evolution Strategies	Adaption and evolution by means of natural selection	Beyer, Schewefel	2002	[19]
BFO	Bacterial Foraging Optimization	Foraging behavior of bacteria	Passino	2002	[20]
FSA	Fish Swarm Algorithm	Schooling behavior of fish	Li, Shao, Qian	2003	[21]
SFLA	Shuffled Frog Leaping Algorithm	Frog leaping on stones in a pond	Eusuff, Lansey	2003 2006	[22], [23]
SCO	Social Cognitive Optimization	Human social cognition	Xie, Zhang	2004	[24]
IWCO	Invasive Weed Colony Optimization	Ecological process of weed colonization and distribution	Mehrabian, Lucas	2006	[25]
ABC	Artificial Bee Colony	Foraging behavior of bees	Karaboga, Basturk	2005 2007	[26], [27]
GSO	Group Search Optimization	Searching behavior of animals and their group living theory	He, Wu, Saunders	2006	[28]
CFO	Central Force Optimization	Metaphor of the gravitational kinematics and particle motion in a gravitational field	Formato	2007 2008	[29], [30]
RFD	River Formation Dynamics	How rivers are formed	Rabanal, Rodriguez, Rubio	2007 2009	[31], [32]
IWD	Intelligent Water Drops	Actions and reactions among water drop in a river	Shah-Hosseini	2007	[33]
RIO	Roach Infestation Optimization	Social behavior of cockroaches	Havens, Spain, Salmon, Keller	2008	[34]
MS	Monkey Search	Mountain climbing process of monkeys	Zhao, Tang	2008	[35]
BBO	Biogeography-Based Optimization	Distribution of species in nature over time and space	Simon	2008	[36]
LCA	League Championship Algorithm	Competition of sport teams in a league championship	Kashan	2009	[37]
GSO	Glowworm Swarm Optimization	Behavior of glowworms – capability to change intensity of luciferin emission	Krishnanand, Ghose	2009	[38]
BBMO	Bumble Bees Mating	Mating behavior of bumble bees	Marinakis, Marinaki,	2009	[39]

	Optimization		Matsatsinis
HSO	Hunting Search Optimization	Group hunting behavior of animals such as lions and wolves	Oftadeh, Mahjoob	2009	[40]
FA	Firefly Algorithm	Flashing behavior of fireflies	Yang	2009	[41]
HS	Harmony Search	Improvisation process of musicians	Yang	2009	[42]
PFA	Paddy Field Algorithm	Reproduction of plant populations	Premaratne, Samarabandu, Sidhu	2009	[43]
GSA	Gravitational Search Algorithm	Low of gravity and resultant mass interactions	Rashedi, Nezamabadi-Pour, Saryazdi	2009	[44]
CS	Cuckoo Search	Breeding behavior of cuckoo – laying color-pattern mimicked eggs in nests of other birds	Yang, Deb	2009 2010	[45], [46]
BIA	Bat Inspired Approach	Echolocation behavior of bats	Yang	2010	[47]
FA	Fireworks Algorithm	Explosion processes of fireworks and mechanisms for maintaining diversity of sparks	Tan, Zho	2010	[48]
PPA	Plant Propagation Algorithm	Propagation of the plants, particularly Strawberry plants	Salhi, Fraga	2011	[49]
CAB	Collective Animal Behavior	Collective behavior of different animal groups such as swarming, milling, migrating in aligned groups	Cuevas, González, Zaldivar, Pérez-Cisneros, García	2012	[50]
WCA	Water Cycle Algorithm	Real world water cycle among transpiration/evaporation, condensation, precipitation	Eskandar, Sadollah, Bahreininejad, Hamdi	2012	[51]
KH	Krill Herd	Herding behavior of krill individuals	Gandomi, Alavi	2012	[52]
BCO	Bacterial Colony Optimization	Behavior of E. Coli bacteria at different development stages in their life cycle	Niu, Wang	2012	[53]
LA	Lion’s Algorithm	Social behavior of lions that helps to keep themselves strong	Rajakumar	2012	[54]
SCO	Stem Cells Optimization	Reproduction behavior of stem cells	Taherdangkoo, Yazdi, Bagheri	2012	[55]
BNMR	Blind Naked Mole-Rats Algorithm	Social behavior of Mole-Rats	Shirzadi, Bagheri	2012	[56]
FPA	Flower Pollination Algorithm	Fertilization/Pollination process of flowers	Yang	2012 2014	[57], [58]
BH	Black Hole	Star swallowing behavior of black holes	Hatamlou	2013	[59]
CA	Cuttlefish Algorithm	Mechanism of color changing behavior adopted by the cuttlefish	Eesa, Abdulazeez, Orman	2013	[60]
MBA	Mine Blast Algorithm	Concept of mine bomb explosion	Sadollah, Bahreininejad, Eskandar, Hamdi	2013	[61]
SSO	Social Spider Optimization	Simulation of cooperative behavior of social spiders	Cuevas, Cienfuegos, Zaldívar, Pérez-Cisneros	2013	[62]
SMO	Spider Monkey Optimization	Foraging behavior of spider monkeys based on fission-fusion	Bansal, Sharma, Jadon, Clerc	2014	[63]
AMO	Animal Migration Optimization	Behavior of animals during migration from one location to another location	Li, Zhang, Yin	2014	[64]
BMO	Bird Mating Optimizer	Mating strategies of birds	Askarzadeh	2014	[65]
FOA	Forest Optimization Algorithm	Seeding procedure of the trees in a forest	Ghaemi, Feizi-Derakhshi	2014	[66]
GWO	Grey Wolf Optimizer	The leadership hierarchy and hunting mechanism of grey wolves	Mirjalili, Mirjalili, Lewis	2014	[3]
VSA	Vortex Search Algorithm	Vortex (swirl) pattern due to vertical flow of affected fluids	Doğan, Ölmez	2015	[67]
WWO	Water Wave Optimization	Propagation, refraction and breaking phenomena of shallow water waves	Zheng	2015	[68]
EHO	Elephant Herding Optimization	Herding behavior of elephant groups	Gai-Ge Wang	2015	[69]
RRO	Raven Roosting Optimization	Social roosting and foraging behavior of common raven	Brabazon, Cui, O’Neill	2016	[70]

• III.    Traveling Salesman Problem

Optimization strives to find the best solution from all feasible solutions. Optimization problem can be either continuous or discrete [71],   [72]. Continuous optimization problems contain variables that can take on real values, such as, solving polynomial equations. In contrast to this, discrete optimization problems, also known as combinatorial optimization problems, contain variables that can take on integer values, such as, the Traveling Salesman Problem.

The Traveling Salesman Problem (TSP) [73]–[75] is one of the most widely studied problems in the arena of discrete combinatorial optimization problems. The basic concept of the TSP is to find a closed tour of a given number of cities, visiting each city exactly once and returning to the starting city, by minimizing the length of the tour.

In mathematical terms, the TSP can be defined as:

• -    Given a weighted graph G = (V, E) , where V is a set of cities and E is a set of edges between cities,

• -    find the tour of all cities that has the minimum total cost, or in other words,

• -    minimize   /(x) = £”_{= T} w i,_i+1 where n is a total

number of cities and w i,i+1 represents distance between city i and its next city in a tour.

With the increase in problem size (number of cities), the total number of possible tours increases exponentially in terms of n! This complexity brings the TSP under the category of an NP-hard combinatorial optimization problem and makes it infeasible to find optimal solution using traditional methods.

The TSP can be either Symmetric or Asymmetric. In the Symmetric TSP, the distance between any two cities is same from either side, while in Asymmetric TSP, this distance is not same. As the back and forth tours are same for the Symmetric TSP, a total number of tours can be given by (n-1)! / 2 .

The positive point of the TSP is its simplicity and easiness in understanding. This prevents the behavior of the algorithm, used to solve the TSP, from being obscured by too many technicalities. Due to this reason, the TSP is used as the test-bed problem in this paper to assess the performance of algorithms discussed later.

• IV.    natural computing and tsp

Careful examination of the natural computing algorithms shows that most of them, particularly recently developed ones, are more inclined towards continuous optimization problems. There are mainly two reasons behind this. First, it is relatively easy to solve continuous optimization problems. Second, it is also easy to map continuous optimization problems with natural phenomena. In contrast to this, discrete or combinatorial optimization problems are difficult to solve and same applies to their mapping with natural phenomena.

In this section, five different natural computing algorithms are described along with their pseudo code, adaptation to solve the TSP and parameters used.

• A.    Genetic Algorithm

Genetic Algorithm (GA), proposed and explored in [6]–[8], has been inspired by Darwin’s theory of evolution, mimicking the process of natural selection for survival of the fittest individual. GA is a populationbased natural computing algorithm that applies various operators such as Selection, Crossover and Mutation to solutions in a population to generate next generation. Three important points to be considered while applying GA to solve any problem are: First, a probable solution must be represented in such a way that it can be encoded on a GA chromosome. Second, each solution must have some fitness function to evaluate it. Third, various operators and parameters must be determined. Important parameters affecting the performance of GA are population size, crossover rate, mutation rate and a number of generation.

• •    Pseudo code:

• 1.  Initialize the Population

• 2.  Evaluate the Population

• 3.    While (Termination Criteria not Met)

• a.    Apply Selection

• b.    Apply Crossover c. Apply Mutation d. Update and Evaluate Population

A population is a set of solutions (chromosomes). Random solutions are generated to initialize a population according to given population size. Each solution is evaluated based on an assigned fitness value. Termination criteria can be predefined a number of generations, maximum allowed time duration or stagnations in the result.

Selection is used to replace worse solutions with better solutions. Crossover is used to generate new offspring by combining genes of selected solutions. Mutation is used to generate new offspring by randomly changing genes of an individual solution. Each solution in a population is evaluated. This process continues until some convergence criterion meets.

Different mechanisms used for selection, crossover and mutation have been explained in [76]. According to it, popular selection mechanisms are – truncation selection, tournament selection, reward based selection, roulette wheel selection (fitness proportionate selection) and rank selection. Popular crossover mechanisms are – k-point crossover, uniform crossover, uniform order-based crossover, order-based crossover, partially matched crossover (PMX) and cycle crossover (CX). Common mutation mechanisms are bit-flip and swap genes.

• •    Adapting GA to TSP:

GA has been adapted to solve random TSP in [77]. Similar to that approach, a solution (or, tour) is encoded as a random permutation for cities starting from 1 to N. Tour length is considered as a fitness value and GA attempts to minimize the tour length in each generation. Tournament selection is used as a selection operator which selects and duplicates better tour between two randomly selected tours. Partially matched crossover is used as a crossover operator as given in [76]. Mutation operator flips cities between randomly selected two points in a tour. Generated tours are evaluated against their tour lengths and the population is updated. This process continues until stagnation occurs in the best tour of the population.

• •    Parameters Used:

Total number of cities = N, population size = 64, crossover rate = 1.0, mutation rate = 0.4, stagnation counter = N.

• B.    Ant Colony Optimization

Ant Colony Optimization (ACO), proposed in [12] and explored in [78], has been inspired by the foraging behavior of real ants. Ants possess natural ability to find the shortest tour between the food source and their nest. Ants deposit a fixed amount of pheromone while Traveling from their nest to food source and vice versa. Initially, they move randomly. An ant having shorter tour will return earlier increasing pheromone value on that tour. Other ants will prefer a tour with higher pheromone value to travel. This results in more and more ants following shorter tour further increasing pheromone value on that tour. In contrast to this, longer tours possess less movement of ants comparatively and so less pheromone value. Also, the pheromone evaporates by a certain amount at a fixed stable rate. These results in the elimination of longer tours after some time and all ants follow the shortest possible tour.

This behavior of ants is modeled mathematically in ACO. This algorithm progresses in an iterative manner. With each iteration, all ants construct their own tour – initially randomly or based on some heuristic value, and later, based on pheromone values on available tours in combination with heuristic values. New pheromone is deposited on tours found by each ant. Also, some pheromone is evaporated from each possible tour. This process continues until convergence occurs, or in other words, all ants follow single tour – probably the shortest one.

In ACO, the pheromone is deposited on tours found by each ant in inverse proportions to their tour length, i.e. depositing more pheromone on better tours and vice versa. In Elitist ACO [78], an extra amount of pheromone is deposited on best tour to increase the chance of selecting that tour by ants in next iteration. The modified Elitist ACO, which is implemented here, deposits pheromone only on the best tour. This results in a faster convergence of the solutions.

• • Pseudo code for modified Elitist ACO:

• 1.    Initialize the Parameters

• 2.    While (Termination Criteria not Met)

• a.    Construct Solutions

• b.    Evaluate Solutions

• c.    Deposit Pheromone on best tour only

• d.    Evaporate Pheromone

All problems need to be converted to graphs to apply ACO. If a problem fulfills this criterion, the given algorithm starts with initializing various parameters such as a total number of ants (M), pheromone matrix (τ), heuristic information matrix (η), evaporation rate (ρ), α and β. Generally, M is kept same as that of a total number of nodes. Each ant is put on the randomly selected node (or city, in the case of TSP).

After initialization, iterative process of algorithm starts. Each ant constructs its own tour (or solution). Once all ants construct their tours, these tours are evaluated according to their fitness function to find the best tour. In next step, the pheromone is updated by evaporating it from all tours and depositing it on the best tour. This process continues until stagnation occurs in the best tour or some other criteria such as predefined maximum iterations or time duration meets.

• •    Adapting modified Elitist ACO to TSP:

The TSP can be easily considered as a graph having each city as a node and a path between two cities as an arc (or edge) between two nodes. To apply modified Elitist ACO to TSP, various parameters are initialized. Pheromone matrix (τ) is initially given unique constant value. During the iterative process of the algorithm, ants construct their own tour. A probabilistic mechanism is used to select next city to be visited from the current city by each ant. Suppose an ant k is currently on city i . It selects next city j to visit based on the probability given by

Pij = МЧпцУ          (1)

Where, Ту and T] .. represents pheromone value and inverse distance between city i and city j respectively. α and β are constant parameters used to control the relative importance of the pheromone values (τ) and the heuristic information (η). As in symmetric TSP any city can be visited from a given city, equation (1) is modified from that of given in [79], [80]. A roulette wheel selection is applied to determine city j based on available probabilities.

Once all ants construct their tours, these tours are evaluated in terms of tour length to find the best tour. In next step, the pheromone is updated by evaporating it from all tours and depositing on the best tour. Pheromone evaporation is performed according to the following equation.

Тц ^ (1 - p)т_ц              (2)

where ρ is the evaporation rate.

Pheromone is deposited according to the following equation.

^та ← ту+1/C             (3)

where C is the length of the best tour.

This process continues until stagnation occurs in the best tour.

• •    Parameters Used:

Total number of cities = N , total number of Ants = N , α = 1.0, β = 5.0, ρ = 0.5, stagnation counter = 50.

• C. River Formation Dynamics

River Formation Dynamics (RFD), introduced in [31], is inspired based on how rivers are formed in nature. Water drops, constitutional elements of the river, flow down to the sea and transform the landscape. Drops erode the ground and decrease altitude while traversing high decreasing gradients. They also deposit carried sediments and increase altitude in flatter areas. Based on decrease or increase in altitudes of nodes, gradients are modified affecting movement of subsequent drops. In this way, decreasing gradients are formed. They represent the path from the source to the sea in the form of a river. These paths model the solutions for the problem under consideration.

• • Pseudo code:

• 1.  Initialize Drops

• 2.  Initialize Nodes

• 3.    While (Termination Criteria not Met)

• a.    Move Drops

• b.    Erode Nodes c.  Deposit Sediments

• d.  Analyze Paths

Similar to ACO, all problems need to be converted to graphs to apply RFD. Mathematical model for the RFD has been elaborated in [31], [32], [81]. This algorithm begins by depositing all drops in the initial node. In next step, all nodes of the graph are initialized by assigning them certain altitudes. A destination node is assigned altitude zero. This node represents a sea. The altitude of all other nodes is set to some equal positive value.

After initialization, iterative process of algorithm starts. Drops are moved based on the altitude difference and distance between two nodes. Based on the movement of drops, nodes are eroded and sediments are deposited. The resultant paths are evaluated in terms of the fitness function. This process continues until stagnation occurs in the best solution, i.e. all drops follow the same path, or some other criteria such as predefined maximum iterations or time duration meet.

Generally, drops move from higher altitude to lower one only. A variation of RFD, called Symmetric RFD (sRFD), is proposed and used in this paper. In symmetric RFD, drops are allowed to move in any direction.

• •    Adapting Symmetric RFD to TSP:

Adapting RFD to TSP is given in [81], [82]. A TSP is modeled as a graph having each city as a node and a path between two cities as an arc (or edge) between two nodes.

RFD is adapted here with some improvements.

Instead of depositing all drops to a single node, drops are deposited to randomly selected nodes to explore the entire search space in a fair manner.

All nodes are assigned same unique altitudes values. They are also eroded initially based on the distance between two nodes as given by the following equation.

erosion=1/dtj(4)

cdtitudej =         - erosion(5)

A probabilistic mechanism selects next node to be visited from the current node by each drop based on the decreasing gradient as given by the following equation.

| altitude;- altitude^ | decGradientij =

The reason behind considering absolute value of the difference between two altitudes is symmetric TSP. For symmetric TSP, a tour in either direction is same. For example, two different tours A-B-C-D-A and A-D-C-B-A have no difference in the context of symmetric TSP. An absolute value of decreasing gradient allows a drop to move in any direction.

Erosion during movement of drops is directly proportional to decreasing gradient. Movement across nodes with high decreasing gradient cause more erosion and vice versa.

Continuous erosion may result in almost zero altitudes for all nodes after some iteration. To avoid this, the altitude of all nodes is slightly increased by depositing sediments after erosion process completes. The amount of sediment to be deposited is considered as average erosion across all nodes.

After updating altitudes, constructed paths by each drop are analyzed in terms of tour length to determine the best tour. This process continues until stagnation occurs in the best tour.

• •    Parameters Used:

Total number of cities = N, total number of Drops = N, stagnation counter = N.

• D.    Firefly Algorithm

Firefly algorithm (FA), introduced in [41] and explored in [83], is inspired based on flashing behavior of fireflies. In formulating FA, three assumptions have been made: First, a firefly is unisexual and can be attracted by any other fireflies regardless of their sex. Second, attractiveness depends on their brightness and varies with distance. Less bright firefly is attracted by brighter one and so moves towards it. A firefly can move randomly if there is no other brighter firefly available. Third, the landscape of the objective function determines the brightness of a firefly. This algorithm models the quality of solution as a brightness of the firefly. A firefly with maximum brightness represents the best solution.

• •    Pseudo code:

• 1.  Initialize the Population

• 2.  Initialize Light Intensity

• 3.    While (Termination Criteria not Met)

• a.    Move Fireflies

• b.  Evaluate and Rank Fireflies

• c.   Update Light Intensity

• d.    Move Best Firefly Randomly

Each firefly represents one potential solution. A population is a set of solutions and initialized with randomly generated solutions. Each solution is evaluated against its fitness function and light intensity (or brightness) is assigned to each firefly based on the fitness value – better the fitness, better the brightness. Termination criteria for an iterative process can be predefined a number of generations, maximum allowed time duration or stagnations in the result.

In each iteration, a firefly is moved towards another firefly based on its attractiveness. A firefly’s attractiveness is proportional to light intensity seen by other fireflies and can be given by

Р = Р_ое"^ ² (7)

where β ₀ is the attractiveness at the origin, r is the distance between two fireflies and γ is a fixed light absorption coefficient. β 0 is determined based on the fitness function.

Once movement of fireflies completes, they are evaluated and assigned ranks to determine the best firefly. Light intensity, β 0 , is updated based on fitness values for each firefly. At the end, best firefly is allowed to move randomly to explore the search space. This process continues until some termination criteria occur.

A variation of FA, called improved FA (iFA), is proposed and used in this paper. Instead of only best firefly, this variation allows a fraction of better fireflies to move randomly.

• •    Adapting Improved FA to TSP:

FA has been adapted to solve TSP in [84], [85]. A solution (or, tour) is encoded as a random permutation for cities. Each firefly represents a single tour. A population is initialized with such randomly generated tours. The fitness of each tour is evaluated in terms of tour length. Light intensity, β 0 , for each firefly is assigned as given by the following equation.

Ро =

tour length

The movement of a firefly has been improved by allowing it to move towards only the best firefly in this paper. Number of steps taken for such movement is randomly selected between 2 and dij as given by, steps = rcm.d.0 m(2, dy) (9)

where, d ij is the hamming distance between two tours. During each step, firefly moves towards best firefly, i.e.

best tour, using inversion mutation, improving its solution quality.

After moving fireflies, each tour is evaluated and light intensities of fireflies are updated. In addition, this adaptation allows top 20% fireflies to move randomly rather than a single best one as suggested in original algorithm. This helps to explore the search space in a better way as well as avoids local minima.

This process continues until stagnation occurs in the best tour.

• •    Parameters Used:

A total number of cities = N, a total number of fireflies = either 10 or N/4, whichever is maximum, stagnation counter = N.

• E.    Cuckoo Search

Cuckoo Search (CS), given in [45], [46], is inspired by breeding behavior of cuckoo – laying color-pattern mimicked eggs in nests of other birds. In formulating CS, three main rules are idealized. First, each cuckoo lays one egg at a time and dumps it in a randomly chosen nest. The number of available host nests is fixed. Each nest (or egg) represents one potential solution. Second, the better nests with high-quality eggs will continue to next generation. Third, the host bird discovers an egg, laid by a Cuckoo, with a probability of P a ϵ (0, 1) from some set of worst nests. In this case, the host bird can either throw away this alien egg or simply abandon the nest and build a new nest.

• • Pseudo code:

• 1.  Initialize Population of ‘N’ Nests

• 2.  Evaluate Nests

• 3.    While (Termination Criteria not Met)

• a.    Randomly Generate New Solution S i from Best Nest

• b.    Randomly Choose Nest  S j   from

Population

• c.    If S i is better than S j Replace S j with S i

• d.    Abandon Worse Nests, Replace with Randomly Generated Nests

• e.    Evaluate Nests

Algorithm begins with initialization of a population with randomly generated solutions. Each solution is a nest (or an egg) and is evaluated against its fitness function to find out the best nest. Termination criteria for an iterative process can be predefined a number of generations, maximum allowed time duration or stagnations in the result.

In each iteration, new solutions are generated by applying random walk or levy flights to the best solution. If these solutions are better than randomly chosen solutions from the population, later ones are replaced. In proportion to given P _a , worse nests are abandoned and replaced with randomly generated solutions. The entire population is evaluated again to find out the best solution. This process continues until termination criteria meet.

• •    Adapting CS to TSP:

CS has been adapted to solve spherical TSP in [86]. Similar to TSP, another problem is PCB Holes Drilling. CS has been adapted to solve this problem in [87].

To represent a random tour, as given in [87], a vector of random values between 0 and 1 is generated. For example, if total number of cities, N = 5, then

S = [0.9134, 0.6324, 0.0975, 0.2785, 0.5469]

S is sorted in ascending order and the relative order of each of the values of S is found. This relative order represents the sequence of cities in a tour as given below.

Sorted S = [0. 0975, 0.2785, 0.5469, 0.6324, 0.9134]

So, city sequence in tour will be, T = [3 4 5 2 1]

A population of N solutions is initialized by randomly generating a set of N different S . Each solution is evaluated in terms of tour length and best solution is determined.

After this, in iterative process, a new solution is generated using equation, new nest =         +a∗ rand. (10)

where α is a constant value and rand represents random values between -1 and 1.

If the new nest has a better tour, i.e. with shorter tour length, compared to randomly chosen nest from the population, the later one is replaced with a new nest.

From entire population, 20% worse nests are abandoned and replaced with the randomly generated tour as given by the following equation.

new nest =          + a ∗ rand       (11)

At the end of each iteration, the entire population is evaluated to determine the best solution. This process continues until stagnation occurs in the best tour.

• •    Parameters Used:

Total number of cities = N, total number of nests = N, α = 0.1, percentage of abandon ( P a ) = 0.2, stagnation counter = N.

• V. Results and Discussion

  Various natural computing algorithms – GA, modified elitist ACO, symmetric RFD, improved FA and CS – have been applied to 8 different TSP instances given in TSPLIB [5] named burma14, ulysses22, eil51, eil76, kroa100, bier127, kroa150, and kroa200. The number in the instance identifier is the problem size in terms of a total number of cities, for example, burma14 has 14 cities. For a stopping criterion, stagnation in the best tour has been used. Derived results have been averaged over 10 different runs. Algorithms have been implemented using MATLAB R2015b and executed on a system with

Windows 7 as an operating system.

Table 2. GA Results for 8 different TSP Instances

TSP Instance	Tour Length			Iteration	Time (Sec)
	Best	Average	Worst
burma14	3462.30	3490.59	3613.91	32.80	0.11
ulysses22	6993.08	7078.62	7282.15	72.60	0.25
eil51	443.47	455.97	471.44	344.50	1.42
eil76	573.21	595.94	610.10	653.00	3.24
kroa100	22123.86	23422.65	25280.06	1189.00	6.90
bier127	123477.30	129260.90	135798.20	2448.60	16.91
kroa150	28181.29	29450.92	31623.33	2486.70	20.34
kroa200	32302.35	33548.14	35078.73	4068.40	46.91

Table 3. Modified Elitist-ACO Results for 8 different TSP Instances

TSP Instance	Tour Length			Iteratio ns	Time (Sec)
	Best	Average	Worst
burma14	3492.17	3523.03	3584.03	12.00	0.03
ulysses22	6993.08	7119.28	7222.63	14.40	0.08
eil51	429.48	442.09	450.34	18.60	0.64
eil76	549.17	560.05	575.62	21.70	1.84
kroa100	21794.41	22382.56	22929.07	24.30	3.90
bier127	121372.10	123031.10	124467.30	29.40	8.13
kroa150	27436.48	28253.22	29352.55	26.60	11.37
kroa200	30563.38	31102.27	31753.81	31.60	27.89

Table 4. Symmetric RFD Results for 8 different TSP Instances

TSP Instance	Tour Length			Iteratio ns	Time (Sec)
	Best	Average	Worst
burma14	3569.32	3625.37	3653.76	15.20	0.06
ulysses22	7097.08	7196.98	7383.61	30.10	0.28
eil51	439.55	449.12	467.57	147.20	5.01
eil76	571.56	577.39	589.80	240.90	35.40
kroa100	22166.38	22706.78	23144.83	124.30	35.02
bier127	125958.10	128379.30	132107.20	101.30	28.70
kroa150	28089.45	28494.95	29262.93	68.50	47.93
kroa200	30330.92	31185.46	32198.42	93.40	142.15

Table 5. Improved FA Results for 8 different TSP Instances

TSP Instance	Tour Length			Iteratio ns	Time (Sec)
	Best	Average	Worst
burma14	3462.30	3474.92	3527.95	23.70	0.06
ulysses22	6993.08	7047.63	7110.34	43.10	0.12
eil51	433.54	443.27	450.09	95.90	0.41
eil76	558.37	569.61	583.45	141.40	1.80
kroa100	21456.26	21876.10	22608.27	180.50	5.14
bier127	120479.80	123247.40	128880.00	222.10	9.79
kroa150	28077.07	28268.49	28588.13	226.20	18.09
kroa200	29630.90	30159.03	30769.78	272.60	51.97

Table 8. Perfective Error (%) for Different NCAs

Instance	GA	eACO	sRFD	iFA	CS
burma14	4.19	5.09	7.41	4.19	4.19
ulysses22	-0.28	-0.28	1.20	-0.28	-0.28
eil51	4.10	0.82	3.18	1.77	2.38
eil76	6.54	2.08	6.24	3.79	3.53
kroa100	3.96	2.41	4.16	0.82	0.06
bier127	4.39	2.61	6.49	1.86	2.19
kroa150	6.25	3.44	5.90	5.86	2.46
kroa200	9.99	4.07	3.28	0.90	0.91
Average	4.89	2.53	4.73	2.36	1.93

The following tables 2 to 6 represent results for various     • Best Tour Length algorithms such as GA, eACO, sRFD, iFA and CS Table 7 represents best tour lengths obtained by respectively. Each of these tables shows best, average & worst tour lengths, average iterations & average time    different algorithms along with optimal tour length as given in [88]. Numbers in bold fonts are best results for a required over 10 different runs for each of the 8 different given TSP instance, while, numbers in italic fonts are .                                                 second best results. Table 6. CS Results for 8 different TSP Instances                This table shows that modified Elitist ACO performs well when problem size is smaller. But with an increase
TSP Instance	Tour Length			Iteratio ns	Time (Sec)	in a number of cities, FA and CS outperform all other algorithms. • Perfective Error Perfective error stands for the difference between optimal tour length and best tour length obtained by an algorithm. Mathematically it can be calculated as, best length—optimal length ∗100         (12) optimal length Table 8 represents the perfective error. Results
	Best	Average	Worst
burma14	3462.30	3515.59	3642.32	22.50	0.02
ulysses22	6993.08	7079.14	7224.24	67.70	0.08
eil51	436.13	443.51	453.62	115.40	0.65
eil76	557.01	570.64	580.25	135.30	1.73
kroa100	21294.40	21863.33	23106.86	223.80	5.09
bier127	120877.70	122941.20	126945.70	359.10	14.61
kroa150	27177.12	27791.13	28546.68	709.80	188.68
kroa200	29635.76	30045.30	30811.75	698.80	113.30
establish the superiority of CS over other algorithms. Also, note that negative error for the TSP instance The performance of algorithms has been compared ulysses22 shows that our algorithms have furnished better –              pnath      ' using five different parameters – best tour length, results compared to optimal results given in [88] . perfective error, precision error, the number of iterations and time required – as discussed below. Table 7. Best Tour Length for Different NCAs

Instance	Optimal [88]	GA	eACO	sRFD	iFA	CS
burma14	3323.00	3462.30	3492.17	3569.32	3462.30	3462.30
ulysses22	7013.00	6993.08	6993.08	7097.08	6993.08	6993.08
eil51	426.00	443.47	429.48	439.55	433.54	436.13
eil76	538.00	573.21	549.17	571.56	558.37	557.01
kroa100	21282.00	22123.86	21794.41	22166.38	21456.26	21294.40
bier127	118282.00	123477.33	121372.14	125958.13	120479.81	120877.71
kroa150	26524.00	28181.29	27436.48	28089.45	28077.07	27177.12
kroa200	29368.00	32302.35	30563.38	30330.92	29630.90	29635.76

• Precision Error

Precision error reflects the failure of an algorithm in providing consistent results. It stands for the difference between best and worst tour lengths in the context of average tour length. Mathematically it can be calculated as, worst length—best length

∗100

average length

Table 9 represents the precision error. Results establish the superiority of FA over other algorithms. For this parameter, CS performs poorly even compared to ACO and RFD.

Table 9. Precision Error (%) for Different NCAs

Instance	GA	eACO	sRFD	iFA	CS
burma14	4.34	2.61	2.33	1.89	5.12
ulysses22	4.08	3.22	3.98	1.66	3.27
eil51	6.14	4.72	6.24	3.73	3.94
eil76	6.19	4.72	3.16	4.40	4.07
kroa100	13.48	5.07	4.31	5.27	8.29
bier127	9.53	2.52	4.79	6.82	4.94
kroa150	11.69	6.78	4.12	1.81	4.93
kroa200	8.28	3.83	5.99	3.78	3.91
Average	7.97	4.18	4.37	3.67	4.81

Table 11. Required Time Duration (in Sec) for Different NCAs

Instance	GA	eACO	sRFD	iFA	CS
burma14	0.11	0.03	0.06	0.06	0.02
ulysses22	0.25	0.08	0.28	0.12	0.08
eil51	1.42	0.64	5.01	0.41	0.65
eil76	3.24	1.84	35.40	1.80	1.73
kroa100	6.90	3.90	35.02	5.14	5.09
bier127	16.91	8.13	28.70	9.79	14.61
kroa150	20.34	11.37	47.93	18.09	188.68
kroa200	46.91	27.89	142.15	51.97	113.30

Best tours obtained for the TSP instance kroa200 by each of our algorithms are presented graphically in figures 1 to 5.

• •    Number of Iterations

Table 10 represents a number of iterations taken by each algorithm to solve the TSP. These iteration values are obtained by subtracting stagnation counter from the total iterations. For example, if stagnation counter is 100 and total iterations are 280, then actual iterations taken to reach to the best solution are 280-100+1 = 181.

These results show that required iterations increase with an increase in problem size for each of the algorithms. Also, it can be observed that modified Elitism approach helps ACO to reduce required number of iterations drastically.

Table 10. Total Number of Iterations for Different NCAs

Instance	GA	eACO	sRFD	iFA	CS
burma14	32.80	12.00	15.20	23.70	22.50
ulysses22	72.60	14.40	30.10	43.10	67.70
eil51	344.50	18.60	147.20	95.90	115.40
eil76	653.00	21.70	240.90	141.40	135.30
kroa100	1189.00	24.30	124.30	180.50	223.80
bier127	2448.60	29.40	101.30	222.10	359.10
kroa150	2486.70	26.60	68.50	226.20	709.80
kroa200	4068.40	31.60	93.40	272.60	698.80

• •    Time Required

Table 11 represents the time required by each algorithm to solve the TSP. The required time is counted only till the best solution appears first time, avoiding the time spent for stagnation period. Required time duration increases with increase in problem size for each of the algorithms.

Results also show that modified Elitism approach helps ACO to reduce required time duration drastically. But if tour length is also considered as solution quality, FA is proved superior.

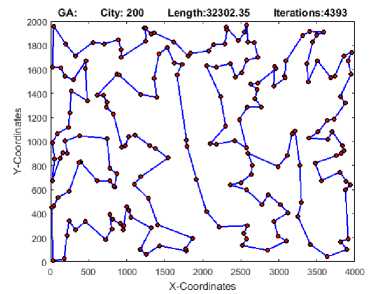
Fig.1. GA Best Tour for TSP instance Kroa200

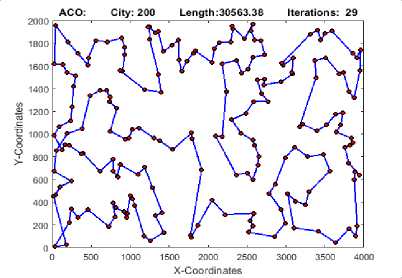
Fig.2. eACO Best Tour for TSP instance Kroa200

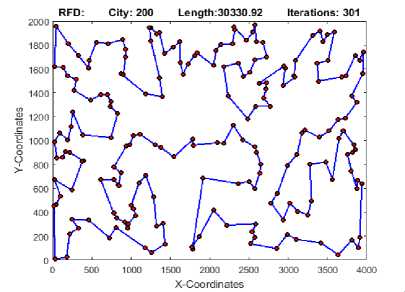
Fig.3. sRFD Best Tour for TSP instance Kroa200

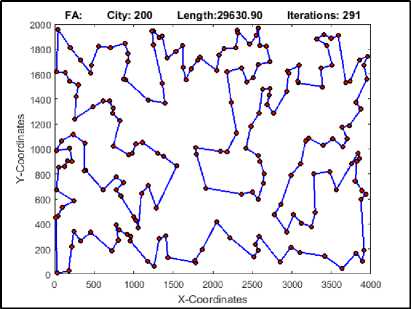
Fig.4. iFA Best Tour for TSP instance Kroa200

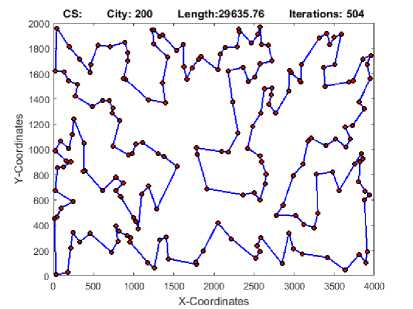
Fig.5. CS Best Tour for TSP instance Kroa200

• VI. Conclusions

  This paper experimentally investigated the performance of five different natural computing algorithms. A summary of the natural computing algorithms, introduced as early in 1970 to as recently in 2016, presented. Five different algorithms – GA, ACO, RFD, FA and CS – implemented with slightly different approaches to solving TSP. GA applied tournament selection, partially matched crossover and flip as selection, crossover, and mutation operators respectively. ACO applied modified elitism approach. RFD allowed water drop to move in any direction. FA allowed top 20% fireflies to move randomly rather than single best one. CS applied real numbered sequence to represent a tour instead of permutation of integer numbers to allow arithmetic operations on solutions.

For smaller city instances all algorithms perform fairly. But with an increase in problem size, their performance degrades compared to FA and CS. Also required iterations and required time increases with increase in problem size. Modified elitist ACO is proved faster. But it fails to provide better solutions to larger problems. CS beats other algorithms with perfection but fails to provide precise results. FA takes less time to converge and provides good quality solutions irrespective of problem size in terms of best tour length, perfective error and precision error. This proves the superiority of FA over other algorithms.